Rep:Mod:GD409 module1
Modelling with Molecular Mechaics
Introduction
The energy of a molecule is minimised using a non quantum mechanical approach, called molecular mechanics MM. This works by using six non-interacting additive terms to find the total energy of a molecule [1]. These are defined as follows:
Dipole-dipole – Sum of all attractions between individual bond dipoles.
Van Der Waals – Using Lennard Jones potential to add up the VDWs repulsions.
Bend – Triatomic bond angle deformations added together
Stretch – Diatomic bond stretches added together
Both stretches and bends can be calculated by Hooke’s Law.
Stretch-bend – Coupling occurs between stretching and bending and this takes both into account forming a correction.
Torsion – Cosine dependence on angles shown by the addition of all the tetra-atomic bond torsions.
Energies were reported in kcalmol-1 and compared using ChemBio 3D programme. The regioselectivity of the hydrogenation of cyclopentadiene dimer and stereochemistry of Taxol were examined using these energy comparisons. Furthermore the regioselectivity of the addition of a nucleophile to dicholorocarbene was examined using semi-empirical MO theory. Glycosidation was also studied using these methods. At the end a mini project was conducted to prove the correct absolute configuration of (-)Cubebol.
Exo/Endo selectivity in the dimerization of cyclopentadiene
Cyclopentadiene in its anionic form C5H5- (Cp) dimerises via a Diels-Alder cycloaddition reaction [4πS+2 πS] of two cyclopentadienes to form two diastereoisomers. At high temperatures the exo isomer forms but the most predominant isomer is the endo according to Baldwin. The minimum energy conformation for each isomer was obtained using MM2.
Thermodynamic control: The kinetic product still forms due to the lower TS energy however there is enough energy to continuously change it back to starting materials as it is a reversible reaction. The thermodynamic product has a higher TS energy which in this case (higher temperature) can be overcome to form the most stable product which dominates.
Kinetic control: Here the lowest energy TS is favoured as very little energy is present in the system (low temperature) hence the reaction is irreversible and the kinetic product dominates.


| Energies/ kcal mol-1 | |||||||
| Stretch | Bend | Stretch-Bend | Torsion | Van der Waals | Dipole-Dipole | Total | |
| Exo isomer | 1.2846 | 20.5810 | -0.8380 | 7.6558 | 4.2335 | 0.3775 | 31.8765 |
| Endo isomer | 1.2497 | 20.8492 | -0.8356 | 9.5103 | 4.3205 | 0.4476 | 33.9975 |
Table 1: Exo and Endo products energies using MM2
Thermodynamically the most stable product is formed which in this case is the exo by 2.12 kcalmol-1. This happens due to a reduction in torsional strain. The reason the endo product is distabilised is due to 1,4-atomic strain present as a result of the molecular symmetry. However the lowest energy transition state favours the fastest reaction and initially forms the kinetic endo product as a result. The endo product has a lower activation energy hence is more dominant as it kinetically occurs faster. This is because the endo TS conformation has an extra stabilisation at the back of the molecule due to the good overlap of the HOMO on the top and LUMO on the bottom orbitals between the two rings leading to a lower energy transition state as shown in the Figure 1 below. Obviously this does not occur in the exo (Figure 2) (otherwise the endo would not dominate under any conditions), which is why it is more stable thermodynamically but has a higher activation energy and hence is slower and less dominant kinetically which agrees with Baldwin’s theory[3].


Hydrogenation of the cyclopentadiene dimer

[4]The hydrogenation of the kinetic endo cyclopentadiene forms a dihydro derivative and if the process is continued all the double alkene bonds are reduced. The force field MM2 is used to minimise the energies in order to obtain the most stable product thermodynamically in the same way as before. Originally the endo form has two double bonds so investigation is conducted to see which one is reduced, hence which of the two possible products form. According to the table below the product 4 is more stable by 4.35 Kcalmol-1 and this is because of the bending or angular strain caused by the bridge of the norborene. The ideal angle of a sp2 hybridised carbon 120° but in product 3 this angle is reduced to 109°. In product 4 the reduced angle between the double bond and substituent alkene is 113° which means it is forced to decrease by a smaller amount resulting in less angular strain so product 4 is selectively formed and more stable. In order to determine if the reaction is under kinetic or thermodynamic control, the transition states of the two products needs to be analysed which cannot happen using the force field MM2 method[5]. Therefore the major product is unknown but structure 4 is more thermodynamically stable due to less angular strain by bending component so lowest in energy.
| Energies/ kcal mol-1 | |||||||
| Stretch | Bend | Stretch-Bend | Torsion | Van der Waals | Dipole-Dipole | Total | |
| Product 3 | 1.2776 | 19.8561 | -0.8349 | 10.8116 | 5.6328 | 0.1621 | 35.6850 |
| Product 4 | 1.0971 | 14.5282 | -0.5495 | 12.4978 | 4.5114 | 0.1406 | 31.1521 |
Table 2: Hydrogenation product energies using MM2
Stereochemistry and reactivity of an Intermediate in the synthesis of Taxol




Taxol synthesis results in atropisomerism where two important intermediate conformers form, structure 9 containing the carbonyl group pointing up and structure 10 which has the carbonyl group pointing down. These separate forms occur due to the high steric demand restricting free rotation about the bond which in this case is a carbonyl. The most stable conformer is determined using MMFF94 and MM2 which are different yet follow a similar trend as shown.
Table 3 Taxol intermediate structure energies| Isomer structure | Minimised energy kcal mol-1 | MM2 Parameters | |||||
| MMFF94 | MM2 | Bend | Stretch | Torsion | 1,4 - Van der Waals | Dipole-Dipole | |
| Isomer 9 carbonyl up chair (chair) | 70.5462 | 47.8396 | 16.5386 | 2.7844 | 18.2485 | 13.1098 | -1.7246 |
| Isomer 9 carbonyl up twist-boat (twist-boat) | 76.2974 | 53.3044 | 17.2104 | 2.9493 | 21.2833 | 14.5043 | -1.7303 |
| Isomer 10 carbonyl down chair (chair) | 60.5593 | 42.6830 | 11.3405 | 2.6203 | 19.6644 | 12.8719 | -2.0023 |
| Isomer 10 carbonyl down twist-boat (twist-boat) | 66.3328 | 48.1579 | 11.8226 | 2.7034 | 22.8891 | 14.3401 | -1.9968 |
| Isomer 9 carbonyl up chair alkane (chair) | -84.94 | 55.2995 | 17.6673 | 2.9715 | 23.0718 | 16.1236 | -1.7740 |
| Isomer 10 carbonyl down chair alkane (chair) | -89.05 | 51.3567 | 14.2265 | 2.8456 | 22.0999 | 15.8809 | -1.7260 |
The two structures were modelled and as it can be seen the lowest energy configuration in each case is in the chair conformation as the strain is minimised as all the hydrogens and atoms are vicinal to each other in a staggered structure. Structure 9 with the carbonyl group facing upwards in the chair is less stable by approximately 9.2Kcalmol-1 than isomer 10. This means that when left to stand the equilibirum lies to the side of isomer 10 so that 9 forms first then changes to 10. Ring flipping occurs and the chair form is more stable than the twist-boat in both cases. When comparing the alkane form to the alkene form in intermediates 9 chair and 10 chair the strain energy can be calculated by subracting the two MM2 total energy values. The diffeence for 9 is -7.46 Kcal/mol and for 10 is -8.6737 Kcal/mol. The negative strain energy is further proof of the very stable (hyperstable) structures. These hyperstable structures often occur at the bridgehead position[6].
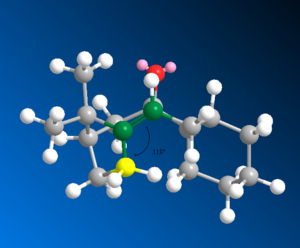
The alkenes are extremely stable as the double bond is nearly at the desired angle (120°) for a sp2 hybridised carbon (119° in this case as shown above) meaning angular strain is minimised so these intermediates hydrogenate very very slowly as they are very stable. When hydrogenantion finally occurs and a single bond forms the sp3 hybridised ideal angle of 109.5° is greatly deviated as the carbon angle is much larger in the alkane being remaining at around 119° which results in high torsional strain reducing the alkene reactivity. The angles are shown below as found by ChemBio 3D. The isomer that is most stable is shown by the MMFF94 and MM2. Also after hydrogenation there are extra hydrogens present which result in transannular strain where in the alkane structure they are closer together resulting in VDWs repulsions increasing. In conclusion the alkene isomers undergo hydrogenation very slowly due to the increase in angular strain and the introduction of increased Van der Waals repulsive transannular H-H interactions. This means the alkene intermediate is much more stable than the product. Very strong conditions are required to cause a reaction[7].
Modelling using semi-empirical Molecular Orbital Theory
Regioselective Addition of Dichlorocarbene

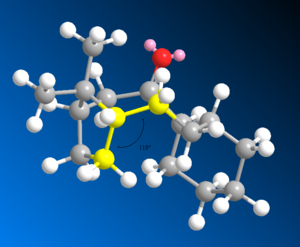
Compound 12 9-chloro-1,4,5,8-tetrahydro-4a,8a-methanophthalene can react with dichlorocarbene (an electrophilic agent) to illustrate the molecular orbital control of reactivity. MM2 is used to minimise the energy in the geometry of the compound and the MOPAC/PM6 method calculates the separate orbital energies displaying them as HOMO and LUMO graphical representations. This is a quantum mechanical method that considers the electron energies.
 |
 |
 |
| HOMO | HOMO-1 | LUMO |
 |
 |
|
| LUMO+1 | LUMO+2 |
The endo double bond is most nucleophilic and this is represented by the HOMO orbital which has the largest amount of electron density. This explains regioselective control where the endo double bond attacks the carbene. In the exo double bond the HOMO-1 π-orbital overlaps in antiperiplanar fashion with the empty low lying antibonding σ* C-Cl LUMO+1, hence is much less nucleophilic and less reactive. This is because as explained electron density is donated away to the C-Cl bond which can stabilise the exo π double bonds making the exo lower in energy and less reactive with less electron density left to donate in order to react.[8].
IR results
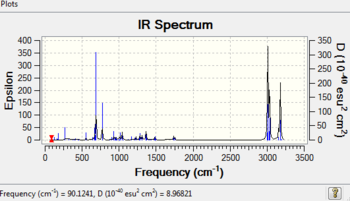
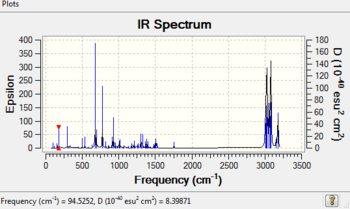
Table 4 IR data of the products (cm-1)
| Bonds | Compound 12 | Compound 13 double bond removed | |
| C=C exo | 1737.04 | none | |
| C=C endo | 1757.44 | 1758.07 | |
| C-Cl | 770.83 | 774.97 |


The π-back donation makes the C-Cl bond weaker in the exo form. This can be shown by IR spectroscopy using a Gaussian method examine the vibration frequencies. After hydrogenation (compound 13)the exo double bond becomes a single C-C bond. In the monoalkene there are 2 more hydrogens which means that the vibrational modes are increased resulting in more peaks in the region of 1000-1800cm-1. The C=C exo has a lower wavenumber so lower energy which backs up the statement earlier where donation occurs from the exo pi bond to the antibonding low lying C-Cl bond, which in turn results in stabilisation and thus lowering of energy of the pi bond. This also means the exo has a weaker bond as electron density is delocalised into the antibonding orbital. This back donation should result in a longer C-Cl bond which is indeed the case as the bond length for the exo is 1.336 while the endo is shorter at 1.334. When the mono hydrogenated product forms the exo double bond is lost so the previous donated electron density from the pi bond is less and as a result of less pi back donation the C-Cl bond is much stronger.
Varying functional group
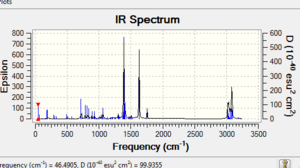
Table 5 IR data EWG and EDG (cm-1)
| Group | EWG (NO2)cm^-1 | EDG (OH)cm^-1 | |
| C=C anti | 1755.98 | 1799.91 | |
| C-Cl | 779.36 | 770.42 | |
| MM2 | 17.4916 | 22.1656 |


With an electron withdrawing group there is less electron density on the C=C anti bond so it has less donation to the C-Cl antibonding making the C-C bond weaker so it has a lower wavenumber and hence lower energy, weaker bond. This is illustrated by the lower stretching frequency and the lower MM2 energy. Also because there is less electron density on the C=C, there is less donation into the C-Cl sigma antibonding which results in a stronger C-Cl as shown by the higher wavenumber. The energy MM2 is lower overall once again as it is more stable. On the other hand with the EDG there is more electron density on the C=C anti which makes a stronger C-C bond with a higher wavenumber due to having more donation. The MM2 has a higher energy as a result. There is little effect on the C-Cl compared to the normal dichlorocarbene due to resonance so perhaps SiH3 should be investigated instead. What should happen is more donation into the C-Cl antibonding and hence a lower wavenumber for C-Cl as the bond gets weaker consequently. However in this case it doesn't change much from the original C-Cl in compound 12. Yet it is still lower wavenumber than the when the EWG is used so proves the theory.
Glycosidation
D-glucose is very important in the formation of carbohydrates. During glycosidation the oxygen lone pair kicks out a leaving droup via the anomeric effect forming an oxonium ion and a nucleophile is substituted in that position. A mixture of α and β anomers can be formed and specific stereocontrol can be obtained by using an acetyl group in place of R group. This happens due to neighbouring group effect where the oxygen lone pair of the acetyl carbonyl stabilises the previously formed oxonium ion, so that the nucleophile can only attack the face that is anti-periplanar to the carbon-acetyl bond and hence not blocked by the sterics formed from the stabilisation. Therefore the protecting acetyl group prevents the nuceophile from approaching either above or below the monosaccharide to create a stereospecific reaction[9].

The diastereospecificity can be investigated using MM2 and MOPAC/PM6 on the 4 possible compounds to minimise energies and interfaces and see the most stable form. The reason hydrogen wasn’t chosen is that it isn’t a protecting group even though it has a low energy. Instead an acetyl group can be chosen but the computational demand is high due to higher energy and the computer process would take longer. Therefore methyl group is used to replace the R as the computational demand is reasonably low and the computer can process it in less than a minute. MOPAC/PM6 is better for comparing the structure energies as the molecular orbitals are taken into account so that electronics are considered. Compound A has the acyl group pointing up and B has the acyl pointing down. However isomers of each form where in A’ the acyl carbonyl oxygen is above the plane and in A it is below the plane. The same is true where for B’ the acyl group is above the plane.
Table 6 MM2 and MOPAC energies (Kcalmol^-1)
| Structure | MM2 energy total | MOPAC/PM6 heat of formation | Stretch | Bend | Torsion | Van der Waals | Dipole/Dipole |
| A SugarA.mol | 24.8697 | -91.65858 | 2.8872 | 11.5788 | 3.6004 | 18.8161 | 5.8692 |
| A' SugarA'.mol | 32.3906 | -75.90716 | 2.3529 | 14.5772 | 0.1479 | 18.2717 | 9.8936 |
| B SugarB.mol | 30.9013 | -88.50810 | 2.9668 | 9.7327 | 6.2711 | 20.0157 | 5.5314 |
| B' SugarB'.mol | 37.9874 | -64.08180 | 2.3322 | 14.6134 | 1.6376 | 18.8991 | 6.3217 |
| C SugarC.mol | 34.5289 | -91.66228 | 2.0967 | 14.3665 | 9.6508 | 17.7322 | -2.0324 |
| C' SugarC'.mol | 46.4095 | -66.84333 | 2.7941 | 18.5030 | 9.0657 | 19.0507 | -1.4405 |
| D SugarD.mol | 45.3547 | -85.93705 | 2.0628 | 16.2869 | 9.6947 | 17.1325 | -1.7470 |
| D' SugarD'.mol | 46.6110 | -66.72179 | 2.9620 | 18.1744 | 9.2502 | 19.2385 | -0.9835 |
The MM2 energies suggest that A and its isomer A’ is more stable than B and B’ in general terms. Also A’ and B’ are less stable than their precursors A and B. This is because in those cases the carbonyul of the acetyl is above the plane so the oxonium cation isn’t stabilised by the oxygen lone pair so is higher in energy. As mentioned before the MOPAC interface is more accurate as it takes into account electronic effects which is illustrated by the smaller difference in energy between the isomers than when MM2 is used. The reason compound A is more stable than B is that the acetyl carbonyl is nearest to the cationic oxonium and is in the right orientation for a better overlap. This means that the oxonium cation is stabilised so is lower in energy as is indeed the case Kcalmol-1 . This energy is lower than for B where the carbonyl cannot overlap as effectively so stabilisation is worse and is higher in energy. These trends were the same for the MOPAC/PM6 but the parameters considered are different. It was explaine earlier why MOPAC is better.
For the remaining C and D the same type of C’ and D’ conformers were formed and the energies were optimized using the same methods. The MOPAC/PM6 are nearly identical for A=C and B=D. Similarly C’ and D’ are the same as A’ and B’ respectively as these structure as simply bonded, that is the only difference. The similarities in value for the C’,A’ and D’,B’ were not as good as the A,B,C and D. The anomeric effect is when the lone pair on the axial oxygen donates electron density into the C-O σ* antibonding orbital which stabilises the bond in a similar way to hyperconjugation. The conformers of C are lower in energy that those of D shown by the table due to this anomeric effect. The MM2 and MOPAC/PM6 shown the same trend but are different (use different parameters). In D no anomeric stabilisation can occur. The conformers for C and D are lower in energy than C’ and D’. This is because in C’ and D’ ring flipping puts everything very close together exchanging each equatorial position with an axial and makes very unfavorable strained interactions as a result of all the molecules being bundled together. This is the reason for their higher energy.
Furthermore the energies of C/C' and D/D' can be used to find their ratio which will in turn determine the diastereospecificity. This works because the quantitative energy difference allows quantitative determination of selectivity. The MOPAC/PM6 energies were used. In this case C/C' = 1.37 and D/D' = 1.29. This shows that the ratio of diastereomers are slightly in favour for C and D.


Miniproject: The synthesis of (-)Cubebol

Cubebol was first identified in cubeb oil as a natural sesquiterpene alcoholand it has a cooling and refreshign taste and used in chewing gum, toothpaste, etc. This project analyses the assignements for the absolute configuration shown below are correct. Furthermore an isomer is tested to see what the preferred conformation is[10]
.

Table 7 '''IR data compared with literature values'
| IR Functional group peaks | Obtained from computational analysis absolute cubebol/cm-1 | Literature/cm-1 | Epimer /cm-1 | Cubebol deviation from literature/cm-1 | Epimer deviation from literature/cm-1 | |
| O-H stretch | 3794.72 | 3491.00 | 3793.99 | 303.72 | 302.99 | |
| C-H bend | 1499.09 | 1490.00 | 1493.25 | 9.09 | 3.25 | |
| C-H stretch | 2992.75 | 2951.00 | 2985.87 | 41.75 | 34.87 | |
| C-C stretch | 1155.35 | 1162.00 | 1171.17 | 6.65 | 9.17 | |
| CH2 bend | 1143.23 | 1142.00 | 1145.56 | 1.23 | 3.56 |
The geometry was minimised with MM2 and the gaussian method (B3LYP) and the Infra-Red spectrum was taken so that it can be compared with the literature values to prove the structure. The IR is shown above and the table below discusses the agreement extent. The was the computer works is by comparing the taylor series expansion to the equilibrium. The reason the OH deviates so highly is because the cubic term in the Taylor series expansion is not taken into account which is an anharmonicity frequency. The deviation from literature for the cubebol absolute configuration is 362.44 and for the epimer it is 353.84. Therefore the epimer conformation is preferred.

Table 8 '''NMR data compared with literature.'
| Carbon | Chemical shift computational (-)-cubebol 1 (ppm) | Difference from literature (ppm) | Literature shift (ppm) | Chemical shift computational epimer (ppm) | Difference from literature (ppm) |
| 8-C | 78.28 | 1.92 | 80.2 | 80.10 | 0.1 |
| 3-C | 39.26 | 5.04 | 44.3 | 39.82 | 4.48 |
| 9-C | 37.38 | 1.62 | 39 | 38.14 | 0.86 |
| 10-C | 34.40 | 1.9 | 36.3 | 35.09 | 1.21 |
| 5-C | 33.99 | 0.39 | 33.6 | 35.21 | 1.61 |
| 7-C | 33.90 | 0.5 | 33.4 | 34.95 | 1.55 |
| 12-CMeMe | 31.61 | 0.1 | 31.7 | 31.98 | 0.28 |
| 16-C | 30.32 | 0.48 | 30.8 | [15-C(26.80)] | none |
| 6-CMe | 30.02 | 0.52 | 29.5 | 30.09 | 0.59 |
| 4-C | 25.13 | 2.77 | 27.9 | 26.61 | 1.29 |
| 1-C | 24.78 | 1.62 | 26.4 | 24.96 | 1.44 |
| 13-C | 23.00 | 0.4 | 22.6 | 23.47 | 0.87 |
| 14-C | 21.32 | 0.22 | 20.1 | 21.72 | 1.62 |
| 2-C | 20.55 | 0.95 | 19.6 | 21.04 | 1.44 |
| 11-C | 19.78 | 1.1 | 18.7 | 19.87 | 1.17 |
This table above shows that the 13C NMR that has been computationally calculated has a strong relationship agreeing with literature values. The difference is never more than 5ppm. The toal deviation from literature is compared for the absolute cubebol conformation and its epimer, the 16-C value is ingored as the epimer contains 15-C instead. The total difference for absolute configuration is 19.05ppm and for the epimer is 18.51 ppm. This means that 4-epimer confromation for cubebol is preferred. In the NMR above the two isomers are very similar however the definitive peak that shows the difference is at 16C for the absolute and 15C for the epimer because the OH group moves.
Here is the epimer:

Optical Rotation
The angle alpha is observed when plane-polarised light passes a path length of 1dm and a concentration of 1g/ml and identifies the chirality. The optical rotation obtained for the absolute cubebol configurations was alpha = -43.87degrees and the literature value is alpha = -48.3degrees. These are reasonably close. The fact that they are both negative is key as it shows levorotatory rotation. This also means they agree so the structures identified using computational methods matches experimental literature value.
3J-J coupling
The coupling using hydrogens is more difficult to use because this means that it is more sensitive to chemical shift so it gives values that should be positive as negative. An example of this is that in the paper a doublet has a coupling constant of 1HZ and for the 3 hyrogens is reported to be at -15ppm. This was backed up using COSY and four bond coupling is possible and usually around 1HZ. However Jonochio allowed 3J coupling which wasn't reported in this paper. This could be because this is a narrow region and so there is a large overlap of lots of signals.
Conclusion
In the NMR above the two isomers are very similar however the definitive peak that shows the difference is at 16C for the absolute and 15C for the epimer. This is due to the alcohol group changing position. In conclusion the epimer term differs less from literature for both the IR and the 13 CNMR so is predominantly formed. Another proof for this is that when the MM2 minimisation was done the epimer had a lower energy by 2.4 Kcal/mol so is more stable. The authors of the paper from which the literature values were obtained calculated the isomer that they assumed they obtained using most likely 2D NMR. In this experiment we used basis set 6,31-G(d,p). That could be another reason for the differences. Overall however it can be said that the epimer definetly is an existing isomer as the computed data correlates better with the experimental literature data than the absolute configuration. The optical rotation shows that the value for the cubebol in its absolute configuration obtained by computed data is the similar to literature.
References
- ↑ Clayden, J.; Greeves, N.; Warren, S.; Wothers, P.; ‘Organic Chemistry’, 1st Ed,Oxford Press,Oxford, 2001,pp. 926
- ↑ F. A. Carey, R.J. Sundberg, Advanced Organic Chemistry: Structure and Mecahnisms 2007, Springer Science, 285-286
- ↑ K. Weissermel, HJ Arpe in Industrial Organic Chemistry 2003, 120
- ↑ J.E Baldwin,Journal of Organic Chemistry,1966,2444
- ↑ N.L. Allinger, Journal of the American Chemical Society 1977, 99, 8130
- ↑ D. S. W. Elmore and L. Paquette, Tetrahedron Letters 1991, 320
- ↑ Wilhelm F. Maier, Paul Von Rague Schleyer, J. Am. Chem. Soc., 1981,
- ↑ B. Halton, R. Boese and H.S. Rzepa Journal of the Chemical Society, Perkin Transactions 2 1992, 440
- ↑ D. Nasipuri, Stereochemistry of organic compounds: Principles and Applications 2005, New International, 340-350
- ↑ D. M. Hodgson, S. Salik, D. J. Fox, J. Org. Chem.,2010, 75, 2157-2169
- ↑ http://hdl.handle.net/10042/to-11841
Cite error: Invalid <ref> tag; refs with no name must have content
