Rep:Mod:FolarinDuduyemiModule2

Computational Chemistry Module 2

Part 1: Generating a molecule of BH₃

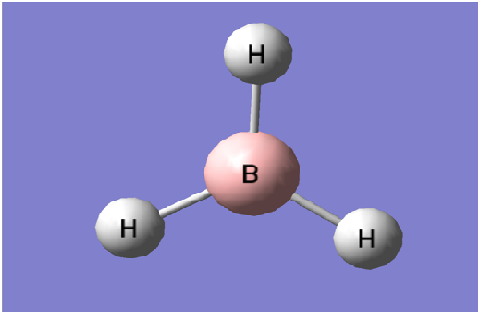
The first step taken was to make a model of BH₃ using gaussview.

An screenshot of the generated molecule is shown below.

The next activity was to practise the following activities using the generated model. -rotation -magnification and shrinking -translation

The B-H bond lengths were then set to 1.50Å.(Prior to this adjustment they were measured as 1.18Å.)

Part 2: Optimising a molecule of BH₃

The next activity to be carried out was optimisation of the BH₃ structure generated. The method chosen was B3LYP. The basis set chosen was 3-21G. The BLYP method determines what type of approximations are made in solving the Schrodinger equation. It is necessary to use approximations in solving the Schrodinger equation for the BH₃ system since analytical solutions for systems more complicated than a hydrogen atom are unavailable. It is noteworthy that the 3-21G basis set in use is of very low accuracy, and so calculations may be carried out relatively quickly.

A link to the log file of the optimised BH3 molecule(generated locally) has been placed below.

OPTIMISATIONLOGFILE

Below is a link to the D-space file

http://hdl.handle.net/10042/to-7633

Part 3: Analysing the optimised BH₃ molecule

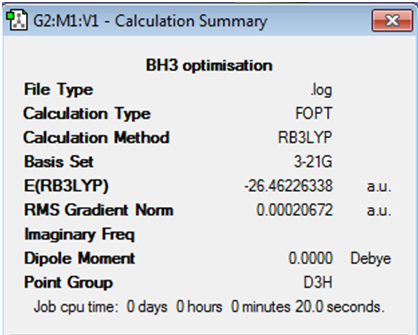
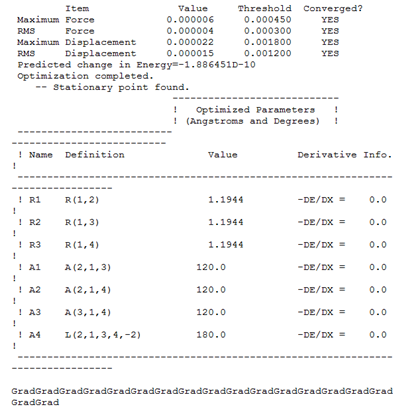
The next step taken was to determine the optimised B-H bond distance and the optimised H-B-H bond angle. The optimised B-H bond distance was found to be 1.19Å. The optimised H-B-H bond angle was found to be 120.0^o

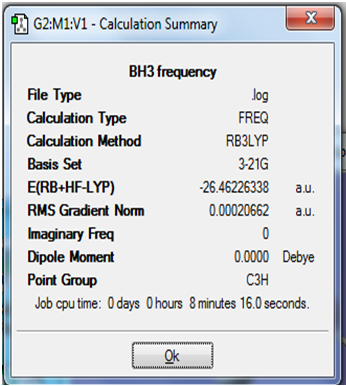
Further information obtained from summary of calculation procedure: A screenshot of the relevant information obtained has been pasted below:

The RMS gradient calculated is very close to zero, and it is less than 0.001, meaning that the optimisation procedure has been completed.

The next step taken was to closer observe the gaussian log file output Importantly, this output file allows us to check the status of the convergence procedure

The forces and displacements can be seen to have converged

Understanding optimisation: part a

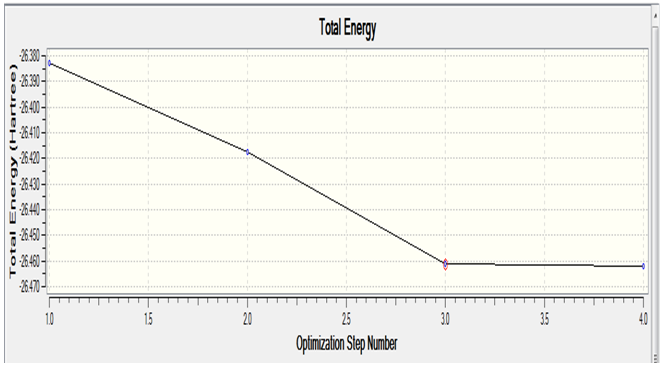
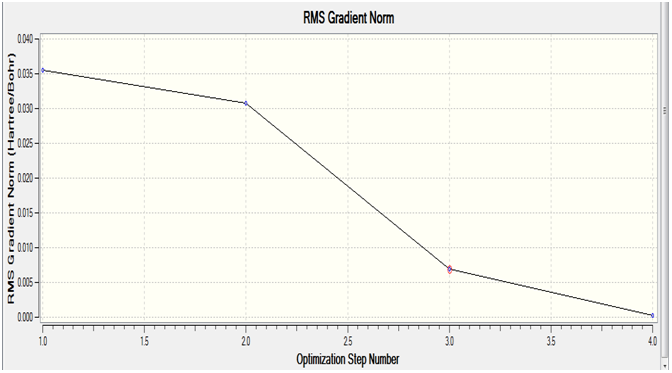
The first plot shows how the total energy varies with optimisation steps

The plot below gives the root mean squared(RMS) gradient of the energy of the molecule at each step of the optimisation

The image below shows the position of the nuclei for the second step of the animation.

As stated in the lab manual, gaussview draws bonds based on a distance criteria, so the fact that gaussview hasn't drawn any bonds doesn't mean they are non-existent, only that they exceed a predefined value. It has also been noted that the last structure has the most negative energy and the smallest gradient.

Understanding optimisation part b

In this section, the focus is to understand the optimisation process. The Born Oppenheimer approximation is a useful tool which simplifies the process of solving the Schrodinger equation. Simply put, for a given amount of kinetic energy, electrons move much faster than nuclei as they are much lighter. Extending this idea, the terms in the Hamiltonian operator relating to the kinetic energy of the nuclei may be eliminated, as the nuclei are considered to be at rest relative to the electrons. Therefore, as stated in the laboratory manual, we obtain an energy which is dependent on the frozen nuclear positions This point may be further illustrated by considering a one-dimensional potential energy surface. At a minimum point, the derivative of the energy with respect to the nuclear co-ordinates(given a single representative value here of R) is zero, and at this point the system is in equilibrium as force, which is the negative of the derivative of energy with respect to R is zero at this point. The plots earlier illustrated give us a means of easily visualising the process of finding the minimum point, as the gradient is close to zero at the final step.

Part 4:The use of pseudo-potentials and basis sets.

As described in the laboratory manual, the presence of a large number of elections in the computation process will require the need to consider relativistic effects, the inclusion of which will result in considerably greater processing time and effort. Bonding interactions are dominated by the valence electrons, and so a useful approximation is to model the core electrons of an atom by a pseudo-potential(PP) or effective core potential(ECP), which makes the process of performing calculations much easier, especially for a many-electron species such as TIBr₃.

What is a basis set(reference:laboratory manual)? A basis set is a means of determining the number of functions used to describe the electronic structure. Usually basis sets able to accommodate a wide variety of functions are more suited to generating experimentally reasonable results than those that are not.

Part 5:Optimising a molecule of TIBr₃

After generating a model of TIBr₃, the symmetry of the molecule was restricted to D_3h, and the tolerance was raised to very tight, in order to prevent difficulties with subsequent vibrations and molecular orbital calculations.

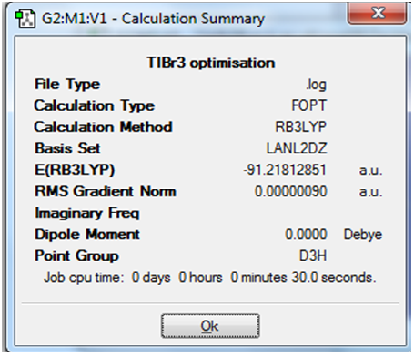
A summary of the most important parameters of the calculation has been pasted below.

A link to the completed TIBr₃ optmisation file has been pasted below.

http://hdl.handle.net/10042/to-7640

The very low value of the RMS gradient of the final step suggests that the optimisation procedure has been successful

The optimised TI-Br bond distance was found to be 2.65Å. The optimised Br-TI-Br bond angle was found to be 120.0^o .

Part 6: Visualising the Molecular Orbitals of BH₃

This was carried out by opening the checkpoint file generated from the optimisation of BH3, setting the method to energy, adding the additional keywords pop=full the purpose of which was to switch on the molecular orbital analysis, and finally by selecting Full NBO under the NBO tab. The 3-21G basis set, which was the same basis set used in the optimisation procedure was specified for use in the method tab.

Below is a link to the checkpoint file needed to visualise the molecular orbitals.

http://hdl.handle.net/10042/to-7643

The first 8 molecular orbitals generated are shown below

Molecular Orbital number	Image
1
2
3
4
5
6
7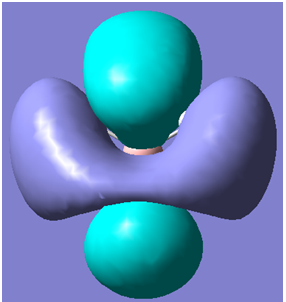
8

Natural Bond Order Analysis of BH₃

This was carried out using the log file of the completed population analysis

As stated in the lab manual, NBO analysis partitions the electron density of the molecule into atomic like orbitals, which are then used to form 2centre-2electron bonds, providing us with information about the extent to which each of the atoms contributes the orbitals needed for forming the bond as well as the hybridisation of the orbitals which these atoms contribute. NBO analysis also provides us with information on molecular orbital mixing.

It was noted however, that there is an unlikely result from these calculations.

Observing the screenshot below, from the log file

The above screenshot relates to the heading 'Bond orbital/ Coefficients/ Hybrids' in which the bonding in the compound is described in the output file. We see that orbital 5 is a lone pair on boron with a hundred percent s character which seems chemically unreasonable, indicating that a higher level of calculation is needed to obtain a more realistic picture.

It also interesting to note that this same orbital which is pictured below

appears pictorially at least to have more p character than s character.

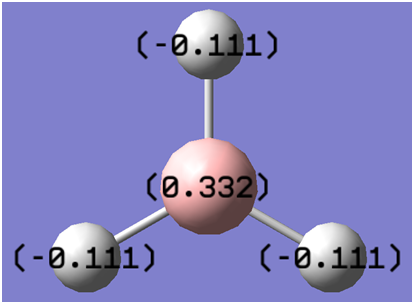
NBO analysis provides a means of quantifying the charges located on the atoms in the molecule. The screenshot below provides an example of this analysis, with bright green indicating highly positive charge and bright red highly negative charge.

The NBO charges on the atoms are shown in the screenshot below(they may also be checked within the linked LOG file)

The NBO charge on borane is given as +0.332, while each hydrogen atom has a charge of -0.111

Part 7: Vibrational analysis and confirming minima.

Vibrational analysis is an important means of confirming that a fully optimised structure is indeed a minimum. According to the laboratory manual, frequency analysis is essentially the second derivative of the potential energy surface, and therefore if all the frequencies measured are positive, then we do indeed have a minimum. Frequency analysis also provides a means of comparing predicted IR and Raman spectra with experimental values.

The energy from our frequency analysis output is shown in the summary below.

Please see link to frequency analysis output log file.

FREQUENCYLOGFILE

This value compares very well with the overall energy of our optimised structure, discussed earlier. A difference in energy beyond the last two decimal places would imply that the structure on which optimisation was carried out is different from the structure on which frequency analysis was carried out, and the calculation would need to be restarted.

Animating the vibrations

Number	Form of the vibration	Frequency	Intensity	Symmetry
1	Hydrogen atoms move in phase towards screen(positive direction), while Boron atom moves in opposite direction(negative)	1144cm-1	93	A2"
2	Both lower hydrogens move in tandem	1204cm-1	12	E' (together with 6)
3		1204cm-1	12	E'(together with 5)
4	All hydrogen atoms have synchronised motion, totally symmetric	2598cm-1	0	A1'
5	The left and right hydrogen atoms move out of phase	2737cm-1	104	E' (together with 3)
6	Left and right hydrogen atoms both in sync. Lower hydrogen atoms are at minimum displacement from Boron atom when the top Hydrogen atom is at the maximum displacement from Boron atom and vice versa	2737cm-1	104	E'(together with 2)

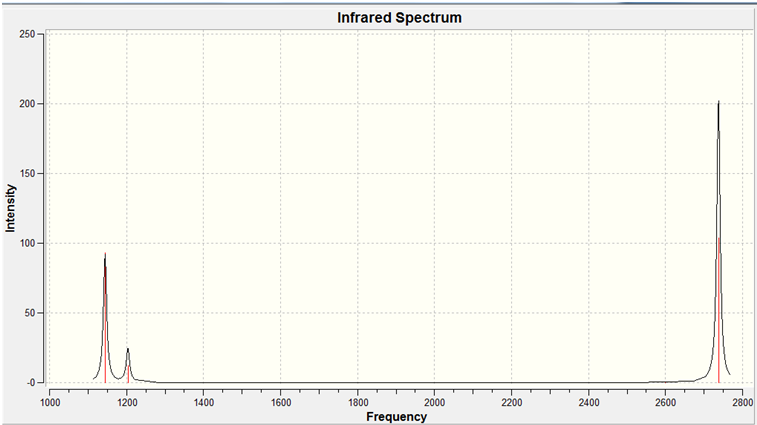
The infra-red spectrum is shown below, with the degenerate bands overlapping and the symmetric stretch having no change in dipole, hence fewer than six peaks are observed.

Summary of information obtained from optimisation and frequency analysis of TIBr₃

Method: It is necessary to appreciate that the underlying theory employed in these calculations is density functional theory(this section is based entirely on the work of Mcquarrie

Several molecular theories are based upon the wave function of the molecule. The wave function of an N electron molecule is a function of N spin co-ordinates and 3N spatial co-ordinates, and physical properties such as energies and geometries are obtained from integrals over all these co-ordinates. If the expectation value for a one-electron operator is to be determined for instance, say A, it can be shown that this value of A can be calculated from the electron density and that the entire wave function, which contains much more information than we need is unnecessary. This is very useful as such electron density may be determined experimentally by X-ray diffraction. According to the reference, the reason that A depends on electron density is that it is a one electron operator. But this presents a problem. The Hamiltonian operator consists of one and many-electron operators, so it doesn't seem likely that the energy could be expressed in terms of electron density. Great progress was made when Pierre Hohenberg and Walter Kohn published two important theorems showing it was indeed possible to express ground state energy as well as other ground state molecular properties as an integral involving the electron density This result is expressed below

E=E(ρ) where the square bracket denotes an integral involving electron density in this case they also showed this equation obeys the variational principle in that

E_O = E(ρ_o) ≤ E(ρ)

These two theorems allowed the bypassing of wavefunctions in favour of electron densities As noted by the reference, the first equation is an existence theorem whereby it was rigorously proven that it is possible to express ground state energy as an integral involving electron density, but the exact nature of this relation is not known. Density functional theory is concerned with the search for the best approximation to this relation.

For the TIBr₃ calculation, the approximation method B3LYP represents an approximation for E[p]-energy as a function of electron density which was developed by quantum chemsits, likely based on the work of Becke,Lee,Yang and Parr.

The basis set used was LanL2DZ, which has been used because of the large number of electrons involved in this model, and thereby the the core electrons of the atoms have been modelled by a pseudo potential(PP) since it is the valence electrons that dominate bonding interactions.

Another issue to consider is why the same method and basis set should be used for both calculations. First, we consider the calculations involved.

1.Optimisation.

2.Frequency analysis.

It is necessary to use the same method and basis set because the nature of the frequency analysis operation in which we find the second derivative of the potential energy surface. If the method or basis set or both the method and basis set are changed, we find the second derivative of a potential energy surface different from that of our optimised structure and this is likely to result in a change of the overall energy of our frequency analysed structure compared to our optimised structure.

As stated previously, the reason for carrying out a frequency analysis is to ensure that our optimised structure is at a minimum in the potential energy surface.

Observing the log. file, FREQUENCYLOGFILE

It can be seen that the low frequencies are -3.4226cm-1, -0.0026cm-1, -0.0004cm-1, 0.0015cm-1, 3.39361cm-1, and 3.39361cm-1, written out to 4 decimal places to allow for differentiation between them. These translate to -3cm-1, 0cm-1,0cm-1,0cm-1,3cm-1 and 3cm-1 to the nearest wavenumber. These values are close to zero and within 10cm-1 of each other, implying a reasonably accurate method has been employed according to the laboratory manual. The lowest real normal mode is of 46cm^-1.

According to the literature, the TI-Br bond length is 2.52Å determined by X-ray structure fine structure spectroscopy and large x-ray scattering of trigonal planar TIBr₃ in aqueous solution. This shows the computed value of 2.65Å for a gas phase model is not unreasonable.

It is also noteworthy that the fact that gaussview does not draw any bonds where we expect does not mean there is no bond, as was seen while animating the first two steps of the optimisation of BH₃. As far as gaussview is concerned, no line has been drawn to represent a bond because the bond length exceeds some predefined value.

The definition of a bond(based on the work of Linus Pauling): 'We shall say that there is a chemical bond between two atoms or groups of atoms in case that the forces acting between them are such as to lead to the formation of an aggregate with sufficient stability to make it convenient for the chemist to consider it as an independent molecular species'.

Part 9: Analysis of the predicted molecular orbitals of BH₃, and comparison with qualitative molecular orbital theory

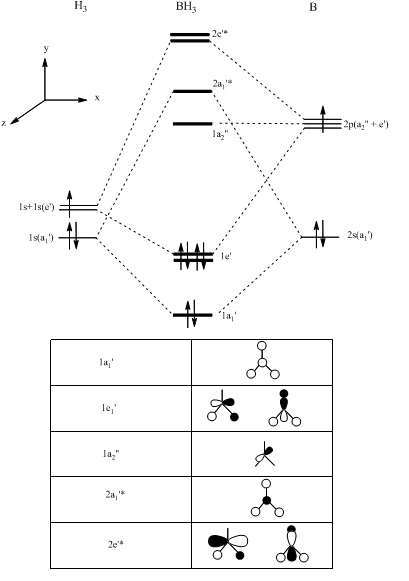
First, the generation of the qualitative molecular orbital diagram.

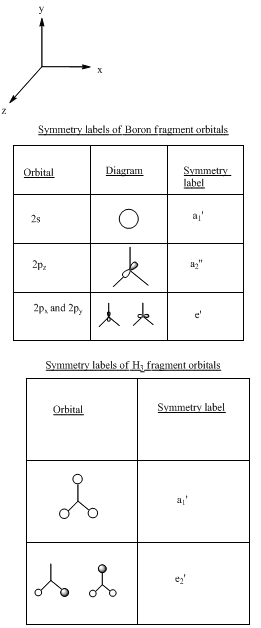
The general procedure for generating a molecular orbital diagram of BH₃ using qualitative MO theory is given below(reference:second year lecture notes on molecular orbital theory)

1. Determine the molecular shape and identify the point group of the molecule.

2. Define the axial system and all of the symmetry operations of the molecule.

3. Identify the chemical fragments and put them along the bottom of the diagram.

4. Determine the energy levels and symmetry labels of the fragment orbitals.

5. Combine fragment orbitals of the same symmetry , estimate the splitting energy and draw in the molecular orbital energy levels and molecular orbitals.

6. Determine the number of electrons in each fragment and hence the central molecular orbital region and add these to the diagram.

7. Identify if any molecular orbital mixing occurs, determine the mixed orbitals and redraw the molecular orbital diagram with shifted energy levels and the mixed molecular orbitals

As stated in the lab manual, the molecular shape has been assumed to be trigonal planar of D_3h symmetry

It is also noteworthy that symmetry fragments have been made use of in this exercise(reference: second year lecture notes on molecular orbital theory) i.e-fragments which contain atoms that transform into each other under the symmetry properties of the group.

The procedure for finding symmetry adapted orbitals(reference: second year lecture notes on molecular orbital theory) is described below

1. Determine the basis orbitals for the fragment.

2. Identify the point group and locate all of the symmetry operations of the molecule.

3. Take the all in-phase combination of the basis orbitals and produce a representation table.

4. Find the contributing irreducible representation using the reduction formula and a reduction table.

5. Determine the orbital co-efficients using the projection operator and a projection table.

6. If there are any degenerate orbitals find the second orbital by guessing and then testing for orthogonality.

7. Produce the full fragment orbital diagram.

The Boron 1s orbital was considered too low in energy to interact with the 1s orbitals of the hydrogen fragments and so has been excluded from the molecular orbital diagram. Making use of the reference, the relative energies of these fragment orbitals have been estimated based on the electronegativity of the atoms involved as well as the extent of the in-phase and out of phase interactions.

Determination of the symmetry labels. .

Building up the MO diagram.

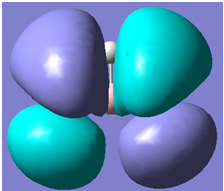
Note: It can be seen from the checkpoint file that the Boron 1s orbital(below) does not mix,

Qualitative versus computed MOs

Qualitative MOs	Computed MOs

It can be seen from the above table that qualitative molecular orbital theory works quite well in this case.

Part 10: Isomers of Mo(CO)₄L₂.

In this section, the main goal is to answer three questions.

1. Which is more stable, cis or trans Mo(CO)₄L₂?, where L=PPh3.

2. How many carbonyl absorption bands are expected in cis or trans Mo(CO)₄L₂ where L=PPh₃.

3. How effectively can L=PCl₃ be used as a model for comparing isomers where L is in fact = PPh₃.

General procedure(reference:Lab manual) Initial optimisation of cis and trans isomers was carried out using B3LYP and the LANL2MB pseudo potential. Loose convergence criteria were set(by adding opt=loose) given that the method employed is of relatively low accuracy and so might not satisfy normal convergence requirements. Upon completion of the optimisation of the LANL2MB structures,(please see link to output file below)

CIS: OPTIMISATIONLOGFILE TRANS: OPTIMISATIONLOGFILE

The torsion angle of the PCl₃ groups were altered in the following way:

1. For the cis conformer one chlorine atom was made to point up parallel to the axial bond, one chlorine of the other group was made to point down parallel to the axial bond.

2. For the trans conformer, both PCl3 groups were set to be eclipsed and one chlorine atom of each group lay parallel to one molybdenum-carbon bond..

After altering the geometries the basis set was chosen to be LANL2DZ and optimisation was carried out.(please see link to optimised files here)

CIS: OPTIMISATIONLOGFILE TRANS: OPTIMISATIONLOGFILE

LANL2DZ is a more accurate basis set. Electronic convergence was increased by adding 'int=ultrafine scf=conver=9' to the 'additional keywords' section.

Frequency calculations were carried out using the method described for the final optimisation. All frequencies were identified as positive, and the overall energies of the output from final optimisation and frequency calculation were sufficiently close to ensure that the structiures on which frequency analysis was carried out was the same as the optimised structure.

Frequency calculation logfile link for TRANS isomer:FREQUENCYLOGFILE Frequency calculation logfile link for CIS isomer:FREQUENCYLOGFILE

Comparison of geometric parameters of optimised structures with experimental data:

A JMOL link to the optimised cis isomer file has been placed below.

A JMOL link to the optimised trans isomer file has also been placed below

CIS data: The source of the data for this comparison is given as: Cotton et al, Inorg.Chem.1982, 21, 294-299 The literature Mo-P distances are 2.576Å and 2.577Å. The literature P-Mo-P angle is 104.6^o . The angle between mutually cis carbonyl ligands is 83.0^o . Mo-C distances trans to the Mo-P bonds are 1.972Å and 1.973Å. Mo-C distances cis to Mo-P bonds were measured as 2.022Å and 2.059Å. C-O distances were given as 1.158Å, 1.149Å, 1.136Å, 1.137Å. The computed Mo-P distances were both 2.51Å. The calculated Mo-P-Mo angle is 94.2^o which is reasonable given Ph has been replaced by chlorine. Calculated Mo-C distance trans to Mo-P bonds is given as 2.01Å, were as for the Mo-C distances cis to Mo-P bonds, the calculated value is 2.06Å, which is close in magnitude to the experimental value, but the differentiation between the two bonds is lost. The C-O lengths are given as 1.17Å for those C-O bonds cis to Mo-P, while the trans lengths are given as 1.18Å. In line with the literature, the trans lengths are greater, but again differentiation between the two is lost.

Overall, the calculated valuables appear very reasonable, even with Ph replaced with Cl for ease of computation.

TRANS data: Data for this section is obtained from the literature source: Hogarth et al, Inorganica Chimica Acta, 1997 254, 167-171 An Mo-P length is given as 2.500Å, while Mo-P was calculated to be 2.45Å. Two C-O lengths are given as 1.164Å and 1.165Å by the literature, where as all C-O lengths were calculated as 1.17Å. P-Mo-P was given as 180.0^o but measured as 177.4^o . The calculated data for the trans isomer also compares well with the literature source.

Comparing the energy of the cis and the trans isomers: It turns out the cis isomer is more stable, and this is for electronic reasons according to the literature.

Quantitatively,

Cis=-623.57707196a.u Trans=-623.57603025a.u Magnitude of energy difference=1.04171 X 10^-3 a.u 1a.u= 4.36 X 10^-18 J.(reference:Quantum Chemistry by Mcquarrie) Energy difference= 1.04171 X 10^-3 X 4.36 X 10^-18 X 6.022 X 10²³ = 2.74kJmol^-1 .

Tuning the stability of cis versus trans It is likely that stability could be shifted to the trans isomer from the cis isomer by using a bulky ligand i.e a very sterically demanding R in PR₃ . The literature states that stability of the cis isomer may be favoured by replacing R=Ph with a pyridyl ring, in which the nitrogen atoms of the pyridyl rings are connected by hydrogen bonding. As a result of the hydrogen bonding, positive charge is shared between the two pyridine rings encouraging cation-pi bonding

Comments regarding the IR Spectra: As expected from symmetry, we compute approximately four carbonyl absorption bands for the compound with cis ligands, while only one is seen in the compound with trans ligands. by approximate, it is meant that carbonyl stretches of negligible intensity are ignored. For the trans isomer, the carbonyl stretch is given as 1951cm^-1 which compares well with the literature value of 1892cm^-1 despite the fact that the phenyl ring has been replaced with a chlorine atom. The computed cis isomer carbonyl stretches are given as 2023cm^-1 1958cm^-1 , 1949cm^-1 and 1945cm^-1 . The literature values are given as 2036cm^-1, 1956cm^-1, 1926cm^-1, 1908cm^-1, 1894cm^-1 . Some values compare well but we obtain a greater number of bands than those predicted by the calculations performed. This may be a solvent effect as the literature readings were recorded in THF which is a good donor solvent.

No negative frequencies were seen, but such frequencies should effectively disappear at room temperature since the energy received by the system is less likely to match the energy gap which is required for such low energy absorptions to occur. Any 'low frequencies' observed are likely to be centre of mass motions(reference:lab manual)

MINI PROJECT

JMOL link for final optimised structure:

The aim of this exercise to investigate the structure of the aluminium analogue of borazine. We begin by visualising the occupied molecular orbitals.

The link to the checkpoint file used in generating these molecular orbitals is indicated below:

http://hdl.handle.net/10042/to-7847

Molecular Orbital number	Image
1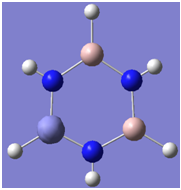
2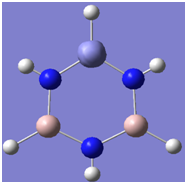
3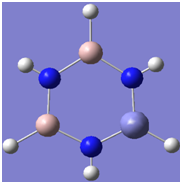
4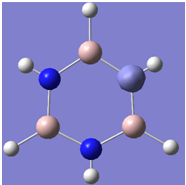
5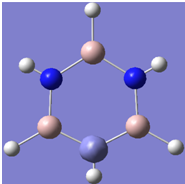
6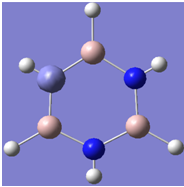
7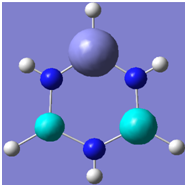
8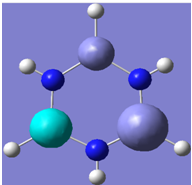
9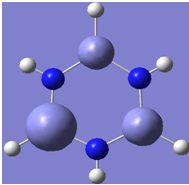
10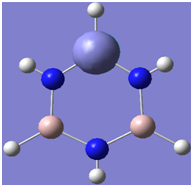
11
12
13
14
15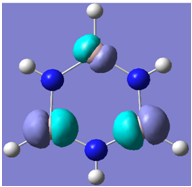
16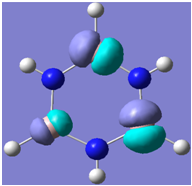
17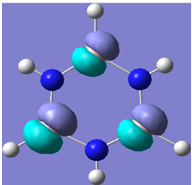
18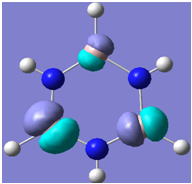
19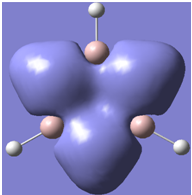
20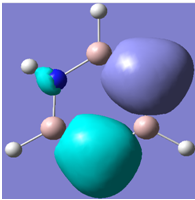
21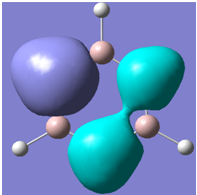
22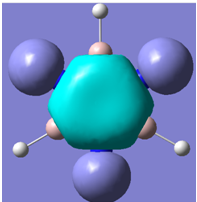
23
24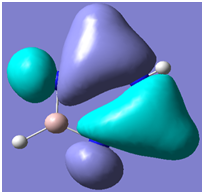
25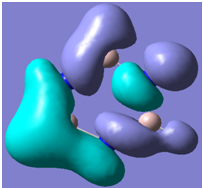
26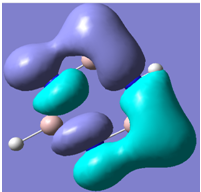
27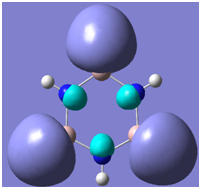
28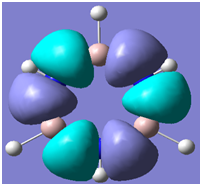
29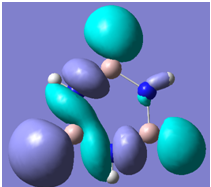
30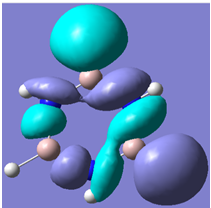
31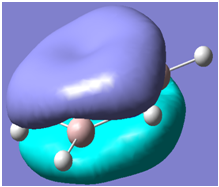
32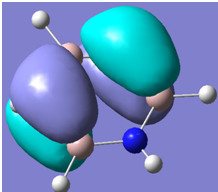
33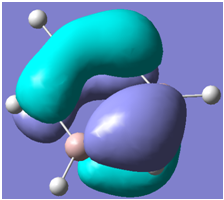

Method Initially, optimisation was carried out using the LAN2MB pseudo potential prior to using the 6-31G,d,p basis set which is a higher level basis set. This was done in order to reduce the computational time of the 6-31G calculation.

A link to the LANL2MB optimised model log file is indicated below:

OPTIMISATIONLOGFILE

A link to the 6-31G, d,p, optimised model log file is also given:

OPTIMISATIONLOGFILE

Frequency analysis was carried out successfully in order to confirm that the structure obtained was in fact at a potential energy minimum. This was done by observing that all frequencies obtained were positive. The frequency analysis log file link is indicated below:

FREQUENCYLOGFILE

Also noteworthy is the fact that there is good agreement between the overall energies of the final optimisation and frequency outputs.

Using the same basis sets as described above, optimisation of a model of benzene was carried out, noting that the symmetry of the model was restricted to D_6h symmetry.

The link to the output file of the first optimisation procedure for benzene is given below:

OPTIMISATIONLOGFILE

A link to the output files for the final optimisation procedure(6-31G,d,p) has also been included:

OPTIMISATIONLOGFILE

Frequency analysis of the benzene model to confirm a potential energy minimum was also carried out.

FREQUENCYLOGFILE

The molecular orbitals of benzene were also visualised using the checkpoint file generated from population analysis

https://spectradspace.lib.imperial.ac.uk:8443/dspace/handle/10042/to-7736

Analysis

A pertinent question is whether the structure under investigation (Al₃N₃H₆) is aromatic. While it is not possible to explore every possible starting conformation for the compound under investigation, the results of the calculation indicate a clear minimum in the potential energy surface for a planar structure, which is unusual given the presence of 'lone' pairs on the nitrogen atom. One method of answering this question is to compare the energy of the model with that of an optimised acyclic, conjugated version and compare their energies(ref:Dr Hunt), another approach involves comparing the calculated molecular orbitals with those of a known aromatic substance such as benzene.

Generally, aromatic compounds are planar(although three dimensional aromaticity is suspected in certain borane structures:reference Second year lecture notes on Main Group Chemistry) , and have a ring current of pi electrons, The linking of p orbitals between the individual atoms strengthens the overlap of the sigma bonding orbitals and thus generates a pi bond which is stronger than a comparable sigma bond, but weaker than a comparable pi bond in an acyclic system due to the localisation of electrons over the whole system, given that only bonding orbitals are occupied(please see output file). The geometry around the nitrogen atoms suggests the lone pairs have taken part in orbital mixing and thus have been stabilised. Indeed, looking at the molecular orbitals, it can be seen that the degenerate orbitals 4,5 and 6 are unusually stable, (orbitals are arranged from 1, lowest in energy to 33, highest energy) being very close to the lowest occupied molecular orbital as opposed to the HOMO as might be expected for lone pairs. This may be due to mixing. Furthermore, all the orbitals occupied are bonding orbitals. It is known that borazine is aromatic, and this problem is of interest given that aromaticity relies significantly on the overlap of orbitals between adjacent atoms. Moving down the group from Boron, there is a greater orbital mismatch between aluminium and nitrogen, but not so much of a mismatch, it seems that the crucial overlap of adjacent p orbitals(seen clearly in orbitals 31-33) which are very indicative of aromaticity is disrupted.

It is interesting to note that the Al-H bonds are longer than the N-H bonds, just as the B-H bonds are longer than the N-H bonds in borazine. This may be due to orbitals 19-22 which concentrate a significant amount of electron density between the nitrogen and hydrogen atoms.

The predicted Al-H bond length is 1.58Å, N-H is 1.02Å, and Al-N is 1.80Å, which does not seem unreasonable given the borazine data( Chem. Ber. (1994) 127, 1887-1889 )(wikipedia reference)