Rep:Mod:FolarinDuduyemi

The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations

Abstract: In this set of exercises, quantum mechanical and molecular mechanical computational methods have been used to make qualitative predictions concerning properties such as reactivity and spectral properties, with some cases backed up with literature evidence. The accuracy of these methods in specific has studies has been assessed. Deviations from reality have been determined(in the quantum mechanical case) to be due mainly to approximations employed in obtaining accurate wavefunctions.

Introduction: The aim of this exercise is to test the ability of specific modelling methods to explain the structure and reactivity of selected chemical compounds in well defined case studies often with literature sources available for correlation with experimental results. The importance of an exercise of this type is that it provides a stepping stone to modelling reactions which are yet to be carried out, potentially saving a considerable amount of time, as well as reducing research costs.

Given the vast spectrum of the complexity of molecules which may have to be modelled by the computational chemist, it is necessary to understand which modelling technique is most suitable for the molecule concerned, especially as regards the kind of information which is required. For instance, it may be best to use a simple molecular mechanics approach to predict which particular isomer may be the major product of a reaction instead of a molecular orbital method which may require a much longer time to give an unnecessarily detailed result. The limitations of the more approximate techniques must also be understood so that they are not applied to systems beyond their scope.

Below is an overview of the molecular modelling methods to be used in this module.

Molecular Mechanics In the molecular mechanics method, the following interactions are considered.

Bond stretching: The potential energy of bonds will take the form of Hooke's law, with the implication that bonds cannot be broken using this method

Bond bending: The bond bending term contributes to the overall potential energy in a similar manner to the bond stretching, illustrated by the equation below which takes a similar form to Hooke's law.

Bond torsion: Measures the barrier to internal rotation of one bond relative to another

Interaction between partial charges: This takes the form of a coulombic interaction

Where q_i and q_j are partial charges on atoms i and j respectively.

Dispersive and repulsive interactions: Given a separation of r, we may specify a Lennard Jones potential to account for these dispersive and repulsive interactions

Hydrogen bonding: This is considered a coulombic interaction in some models, but is also considered as an interaction represented by the equation below in other models.

The molecular mechanics approach however suffers from the disadvantage of relying on data from well characterised molecules, apparently undermining the stated objective of this exercise in simulation.

Semi empirical molecular orbital methods: These methods are far less reliant on known properties of molecules compared to molecular orbital methods but are limited by the lack of known analytical solutions to the schrodinger equation for systems more complicated than a hydrogen atom. Therefore, several approximations are made using this approach. It is noteworthy however, that the errors resulting from these approximations may be negligible in the context of what can be measured experimentally, making semi empirical molecular orbital methods potentially very accurate.

What to look out for: Results of modelling techniques employed, specifically the relative magnitudes of calculated total energies, and comparison of the results obtained with the relevant literature.

Case study 1: The Hydrogenation of the Cyclopentadiene Dimer.

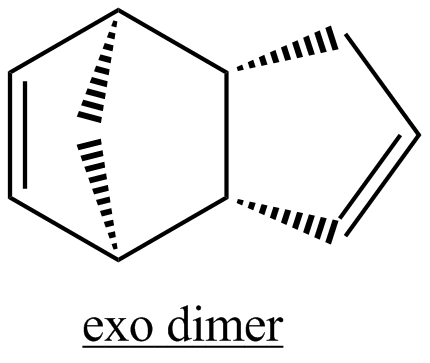
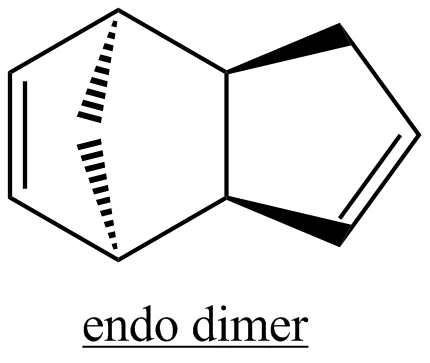
The first task is to rationalise why cyclopentadiene dimerises to produce specifically the endo dimer rather than the exo dimer. Both have been illustrated below.

The table below shows the output of results obtained by running the MM2 calculation

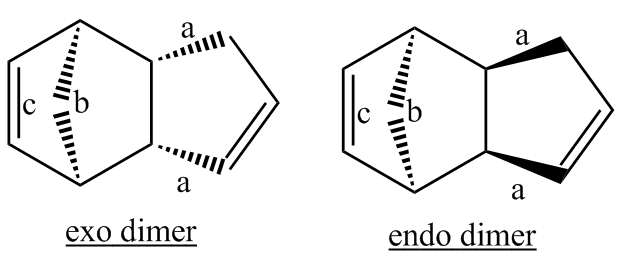
The total energies of the exo and endo isomers are very similar, indicating that the strong bias towards formation of the endo isomer is unlikely to be due to thermodynamic control. The results show that the endo isomer is the more hindered in a thermodynamic sense, indicating that the selectivity observed is likely due to kinetic control. The most significant contributor to the difference in energy of the two isomers is the torsional contribution. This may also be understood by considering the single carbon atom bridge as well as the double carbon atom bridge across the ends of the new C-C bonds formed. The exo product is more thermodynamically favourable as there is a reduced amount of steric hinderance if the the single carbon atom bridge eclipses the cyclopentene ring as opposed to the double carbon atom ring.

This point is further illustrated by the diagram above in which b denotes the single carbon atom bridge, c denotes the double carbon atom bridge, and a represents the newly formed bonds.

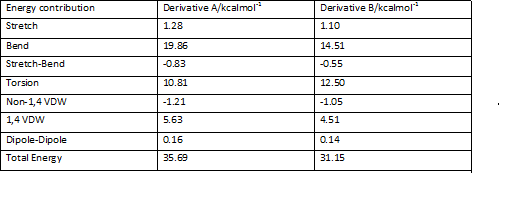
The table below shows the output of results obtained by running the MM2 calculation

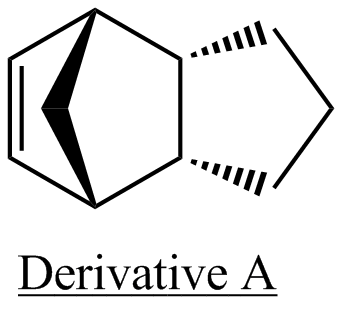
Given the data in the above table, it cannot be deduced whether the preferential formation of derivative A or deribvative B, as a result of hydrogenation of the endo isomer is due to thermodynamic or kinetic control. What can be deduced however, is that if the reaction were to proceed under thermodynamic control, then derivative B would be formed preferentially. Also, derivative B may still be formed preferentially even if the reaction proceeds under kinetic control. Transition state modelling is required for further analysis. It can be seen that the most significant difference in energy between derivatives A and B is due to the bending contribution, with A having a much higher bending contribution. Another significant contributor to the difference in energy between the two species is the 1,4 van der waals interaction which is again higher in derivative A.

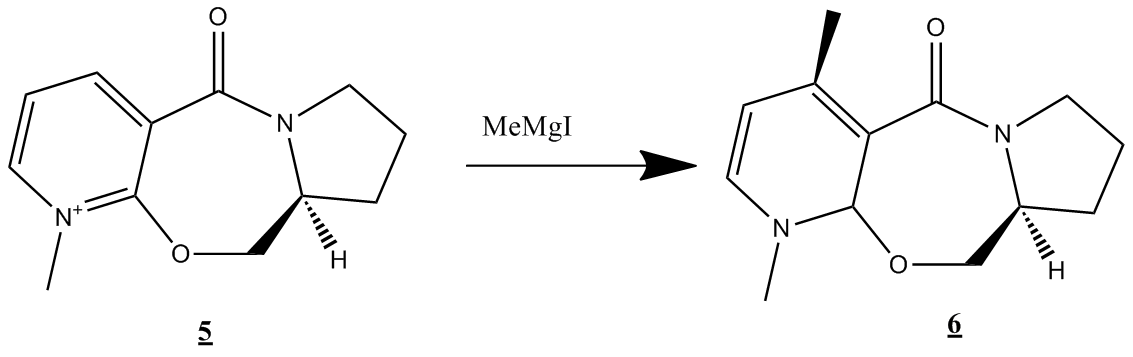
Case study 2: Stereochemistry of nucleophilic additions to a pyridinium ring analogue

First, stereochemical control of the reaction below will be studied

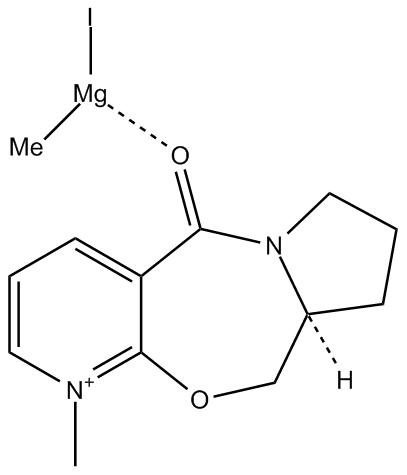
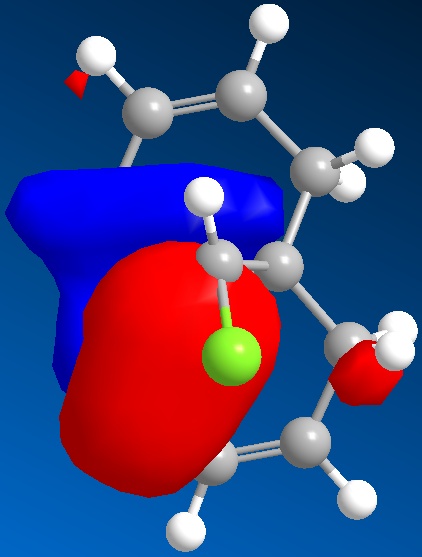
An MM2 force field was initially used to carry out this simulation. The lowest energy result of this MM2 force field energy minimisation on molecule 5 was a total energy of 43.11 kcal/mol, crucially with the carbonyl oxygen remaining in the same plane as the phenyl ring. Various starting geometries were tried out, particularly for the carbonyl group oxygen. The minimized geometry is illustrated below

Attempting to run the minimisation with the MeMgI present as a separate structure gives the error message:no atom type was specified to the selected atoms, with the Mg atoms highlighted. This is due to the fact that the molecular mechanics method does not allow for species with broken bonds, due to the quadratic bond stretching potential.

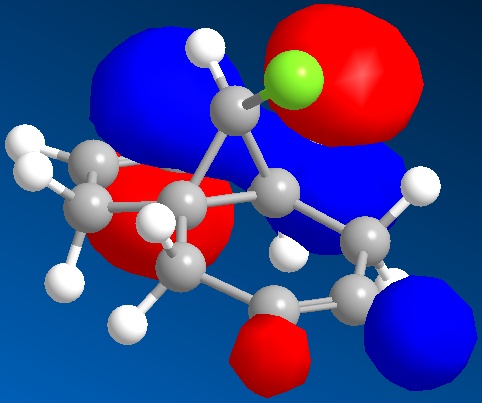
Modelling was then carried out using Mopac. Using the PM6 method, it was seen that the resultant minimised structure had an overall energy of -2600eV and crucially, the starting point was a conformation in which the carbonyl oxygen was in the same plane as the phenyl ring, but the minimised structure had the carbonyl oxygen out of the plane of the phenyl ring and directed in the opposite direction to the chiral hydrogen. This is illustrated below

In accordance with the literature the result of chelation control and the intra-molecular delivery of the methyl group through a six-centred transition state gives the absolute stereochemistry shown in the product.

Investigation of the reaction indicated below was then carried out:

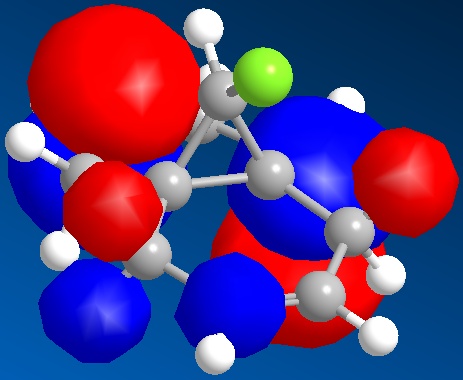
Minimisation using the PM6 force field gives a total energy of -3650eV, with the carbonyl oxygen anti to the orientation of the non-aryl methyl group and out of plane to the pyridinium ring. This is illustrated below

The literaturestates that this out of plane orientation provides steric hinderance to attack from one ring face resulting in the absolute configuration of product seen. However, the methyl group would appear to provide some considerable steric hinderance of it's own to attack by the lone pair bearing nitrogen on the side of the pyridinyl ring which leads to formation of the product. Both of these models may be improved by evaluating the symmetry of the molecular orbitals of the reactants, as well as comparing their energies, to predict the likely mode of reaction i.e the direction of approach to achieve the best orbital overlap.

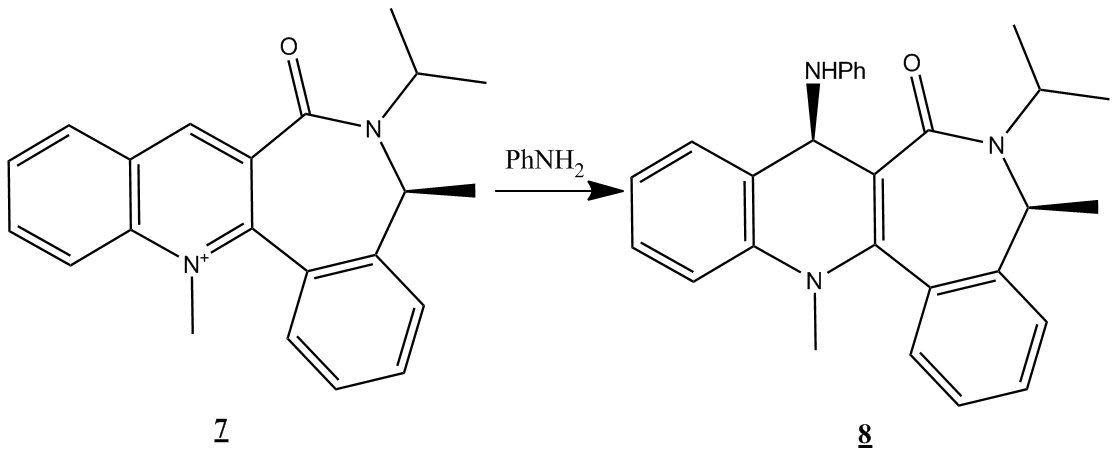
Case study 3: Stereochemistry and Reactivity of an intermediate in the synthesis of Taxol:

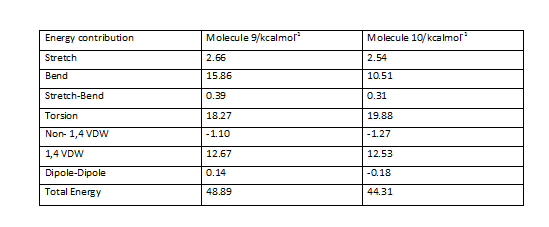
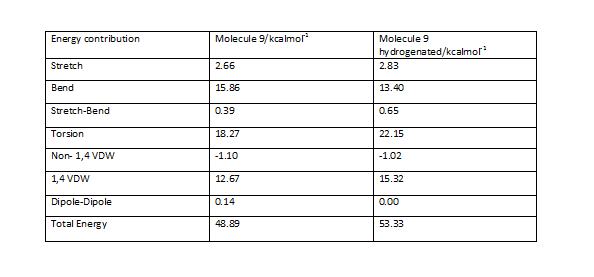
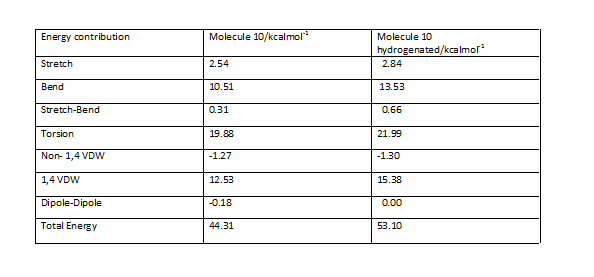
Intermediate molecules 9 and 10 have been subjected to MM2 force field minimisation and the results have been indicated below

Jmol of minimized intermediate molecule 9

Pentahelicene

Jmol of minimized intermediate molecule 10

Pentahelicene

A comparison of the outputs obtained is shown here

The results obtained show that intermediate 10 is of greater stability mainly as a result of bending energy difference.

Rationalisation of the unreactivity of the alkene: This will be done, not in an absolute sense, i.e how stable are these particular alkenes relative to every other type of molecule, but by considering the consequence of having these alkenes react and generating two sp³ hybridized centres as opposed to two sp² hybridized centres.

The energy of a minimized hydrogenated species of molecule 9 has been compared with the energy of the unreacted model of molecule 9.

We can see clearly an increase in energy of the model upon hydrogenation due to significant increases in 1,4 van der waals interactions as well as torsional energy.

Similar results are seen in comparing the hydrogenated model of molecule 10 with the unreacted model with the difference in bending energy now being a significant contributor.

In accordance with the literature,, it can be seen that bridgehead olefins have negative olefin strain energies, in line with computational(Allinger MM2 force field) and experimental results.

Modelling using Semi-Empirical Molecular Orbital Theory

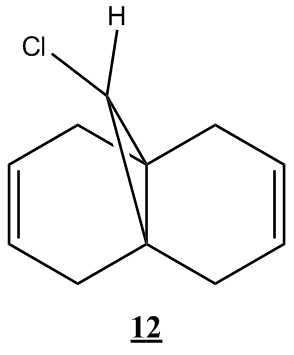
As was done with the molecular mechanics method, investigations were carried out using a case-study format. The first task was to explain the relative nucleophilicities of the endo and exo alkenes in the molecule(molecule 12) illustrated below.

This was done by first minimizing the energy of the model using an MM2 force field, then using a Mopac/PM6 method to observe the Highest Occupied Molecular Orbital(HOMO).

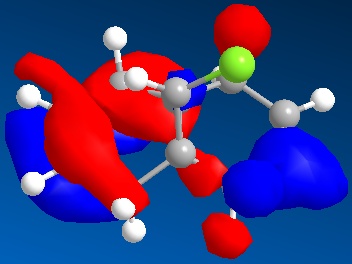
The HOMO is illustrated below

The HOMO shows that the endo alkene possesses greater electron density than the exo alkene as seen by the location of the exo alkene within a nodal plane, while the endo alkene is enclosed by a molecular orbital of a single phase. Thus the endo alkene is expected to be more nucleophilic in line with the literature

The HOMO-1 is shown below

The LUMO, LUMO+1 and LUMO+2 have all been illustrated.

LUMO

LUMO+1

LUMO+2

The vibrations of molecule 12 were inspected by applying gaussview to the geometry optimized, frequency evaluated model. The main C-Cl stretch of magnitude 902cm^-1 is seen to result in a periodic, but symmetric motion of the two rings containing the alkenes. The exo C=C stretch frequency is 1737cm^-1 while the endo C=C stretch frequency is 1757cm^-1 which makes sense given that the HOMO shows a greater electron density at the endo alkene compared to the exo alkene. The exo hydrogenated model shows no discernable C-Cl stretch in the gaussview program. The endo C=C stretch frequency is given as 1758cm^-1 which is hardly a change from the model of molecule 12. The influence of the C-Cl stretch on the vibrational frequencies of the molecule may be understood by considering the fact that the geometrical distortion observed in the geometry minimized model of molecule 12 is stabilized by an interaction between the sigma star C-Cl orbital and the exo alkene pi orbital. In molecule 12, the interaction between these two orbitals destabilises the sigma antibonding orbital of C-Cl , thereby stabilising the C-Cl bond and increasing the frequency of the C-Cl stretch. The absence of this stabilising interaction in the exo-hydrogenated model of molecule 12 lowers the energy of the sigma antibonding C-Cl orbital, and lowers the energy of the C-Cl stretch. Based on this model, it can be predicted that placing increasingly electron withdrawing substituents on the exo alkene will lower this stabilisation, leading to weaker C-Cl stretches in the non-hydrogenated models, weaker and exo C=C stretches in the non=hydrogenated models. Observing a =C-OH exo substituted model, the energy of the exo C=C stretch is seen to be 1797cm^-1 while the energy of the endo stretch remains virtually unchanged. The stretch which closest resembles a C-Cl stretch is seen to have an energy of 552cm^-1 . The C-Cl stretch energy follows the expected trend but the higher C=C stretch energy may be explained by considering that such a motion cannot occur without motion of the -OH groups, increasing the overall energy of the stretch.

Structure based Mini project using DFT-based Molecular Orbital Theory

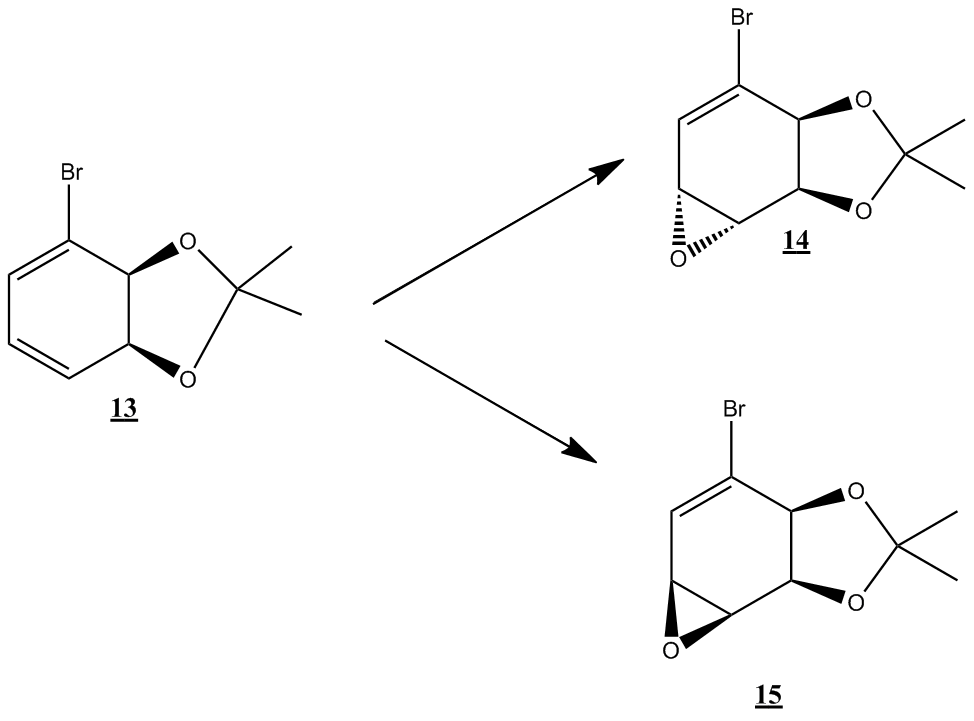
Regio and stereoselective conversion of alkenes to epoxides Consider the conversion of compound 13 into compounds 14 and 15.

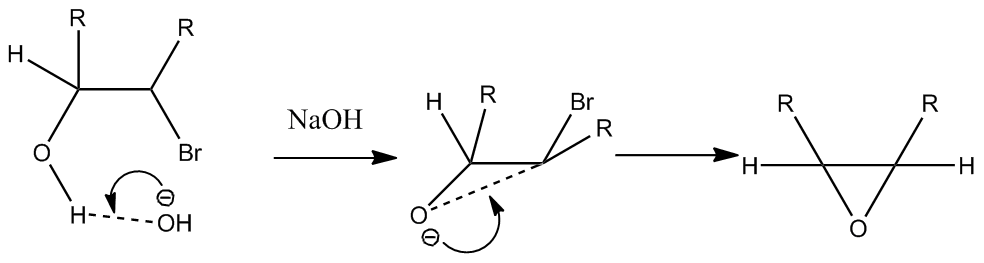
According to the literature, the conversion of 13 into 14 occurs under conditions of m-CPBA, dichloromethane, and room temperature. The fact that the reaction occurs at room temperature may be attributed to the low energy transition state of the reaction mechanism, and the stereochemistry of compound 14 is the result of attack by m-CPBA on the less hindered face. The conversion of of compound 13 to compound 15, according to the literature occurs under conditions of i) NBS THF-H₂O, and room temperature, and then ii) 5M NaOH, Et₂O-H₂O, and 40^oC. Under these conditions, a bromohydrin is formed at the end of step one, with the bromine atom located anti to the bulkier oxygen containing groups as a result of steric hinderance. Under basic conditions, deprotonation of the alcohol follows with the bromide expelled as a leaving group and an epoxide is formed via intra-molecular S_N2 with the back-side attack of the oxygen anion being responsible for its eventual orientation in molecule 15.

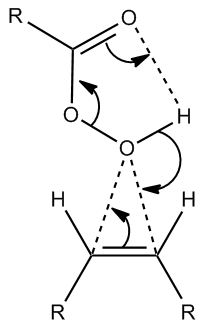
An illustration of the mechanism of epoxidation by m-CPBA is given below

Below is an illustration of bromohydrin and subsequent epoxide formation

Differentiation between compounds 14 and 15 by spectroscopic means

An important technique in this regard is the use of the optical rotation property where both compounds differ significantly. Using the cambridge variation on the B3LYP density functional method and the 6-31G(d.p) basis set, the optical rotation of molecule 14 was predicted to be 125^o at 589nm. This compares reasonably well with the literature value of 103.8^o at 589nm. The optical rotation of molecule 15 was predicted using the same method to be -115^o at 589nm compared to the literature value of -76.2^o.. Here, the calculation is less accurate, but it is important to note that the sign of the optical rotation was correctly predicted in each case, and therefore a researcher could have been provided with a means of identifying each isomer without knowledge of experimental work in various literature.

Analysis of the ¹³C NMR spectra

The literature ¹³C NMR of molecule 15 is given by the literature as follows:

13C NMR(CDCL3):25.2(s), 27.1(s), 50.2(s), 54.5(s), 73.9(s), 76.8(s), 108.7(s) 125.5(s), 130.0(s)

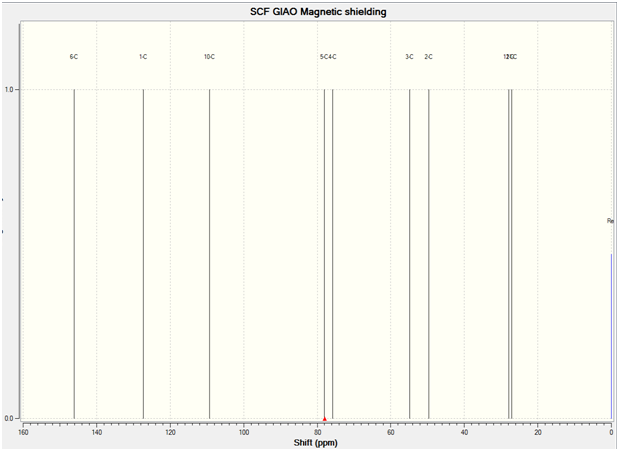
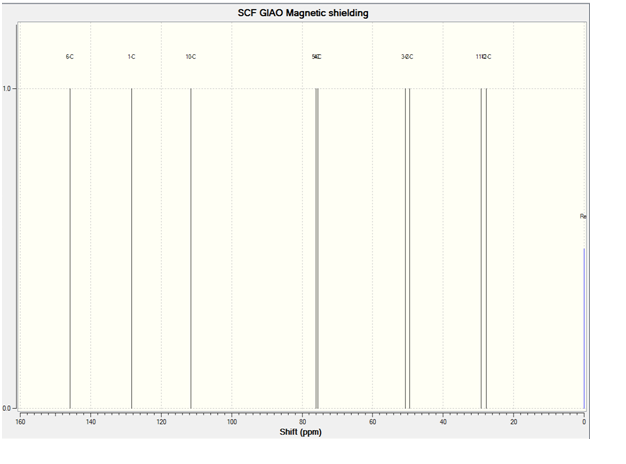
The predicted 13C NMR Spectrum is shown below:

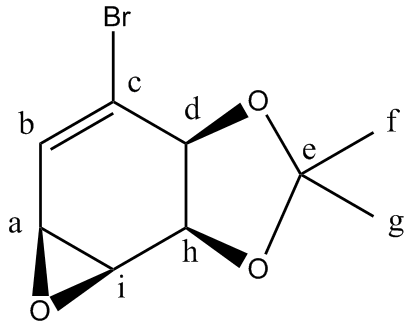
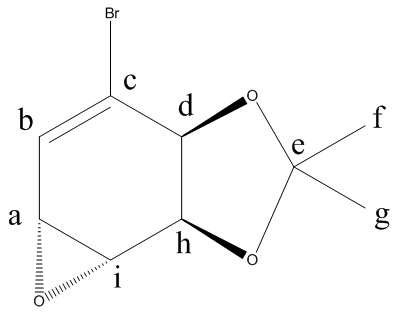
¹³C NMR(CDCL₃):27.2(s)(C_f-oriented towards the ring)), 27.9(s)(C_g-oriented away from the ring), 49.7(s)(C_a), 54.8(s)(C_i), 75.7(s)(C_h), 78.1(s)(C_d), 109.4(s)(C_e) 127.3(s)(C_b), 134.1(s)(C_c)

The comparison between the predicted and literature 13C NMR is quite good. The carbon atom attached to the bromine atom however, had to have its chemical shift reduced by 12 to correlate better with the literature.

The predicted ¹³C NMR Spectrum of molecule 14 is shown below:

¹³C NMR(CDCL₃):29.2(s)(C_f-oriented towards the ring)), 27.7(s)(C_g-oriented away from the ring), 49.5(s)(C_a), 50.7(s)(C_i), 75.5(s)(C_h), 76.0(s)(C_d), 111.6(s)(C_e) 128.4(s)(C_b), 133.9(s)(C_c)

As can be seen from the ¹³C NMR data, ¹³C NMR Spectroscopy is a poor means of differentiating between molecules 14 and 15 by computational methods, and this is reasonable given the high level of similarity in both structures

Another spectroscopic method of differentiating betwen molecules 14 and 15 is to use 3JHH couplings. Here, this has been done using Janocchio, employing a simple method based on the Karplus equations.

The results have been indicated below:

Molecule 14: ³J_HH(a and b) 7.68Hz, 3J_HH(i and j) 3.41Hz, Molecule 15: ³J_HH(a and b) 6.62Hz, 3J_HH(i and j) 4.83Hz.

It can be understood from this application(which is admittedly approximate) that these specific couplings may be differentiated within the experimental results