Rep:Mod:Fleur777

The Cope Rearrangement

The reaction to be modelled is shown in the figure below, it is a [3+3] cycloaddition, which involves 4 pi and 2 sigma electrons and hence should proceed via a concerted mechanism with only suprafacial components (when the reaction is heated) according to the pericyclic selection rules.

The purpose of this exercise is to use molecular orbital-based methods to locate the low-energy minima and transition structures on the 1,5-hexadiene potential energy surface in order to deduce the preferred reaction mechanism and see if this is in accord with what is expected.

Cope rearrangement of 1,5 hexadiene

This cannot be done by molecular mechanics as this is an empirical method that does not consider the electron positions but rather uses the average electron density in the molecule in the calculations it uses to compute the total energy of the molecule. These calculations use empirical data (often derived from experimental values) in order to give a realistic final energy value. Hence they don’t show transition structures or show bond making or breaking. This arises as a result of the bonds being explicitally defined, hence the only energy maxima that can be found are high energy conformers of the starting molecule put into the calculation.

A potential energy surface for the reaction can be found from these methods by plotting the potential energy curve for stretching the bond that is breaking and the potential energy curve for stretching the bond being formed on the same axis and defining the transition state structure as the point at which they cross. (This is due to the Frank Condon principle). Expand/state! For this kind of calculation better results are obtained using a Morse potential for bond stretching than if a harmonic one is used.

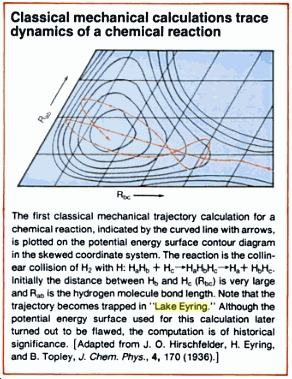
Example of a potential energy surface obtained by classical methods

In order to describe the bond making and breaking processes (and gain information on the transition state structure and energy) the Schrodinger equation must be solved numerically and the molecular orbitals computed so that changes in electron distribution can be seen. This is important for the given reaction as the reaction mechanism (and hence structure of the transition state) depends highly on the reactants having correct orbital symmetry and overlap.

Optimising the reactants and Products

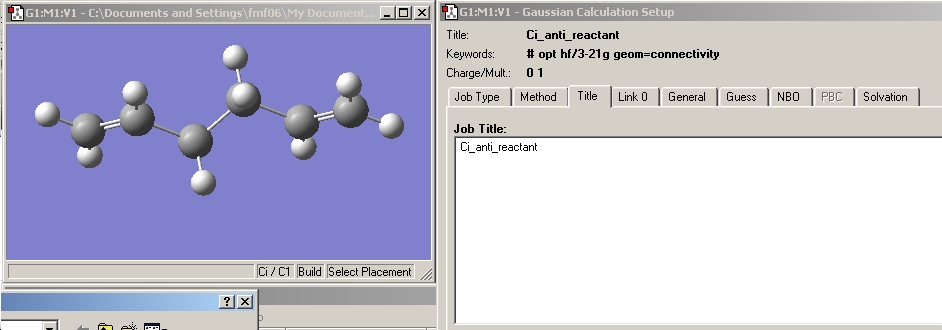
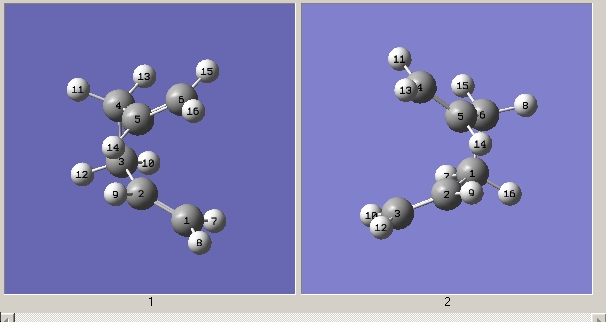
1,5 hexadiene was drawn in gaussview with an anti linkage of the 4 central carbons. This structure was cleaned and the resulting molecule can be seen below.

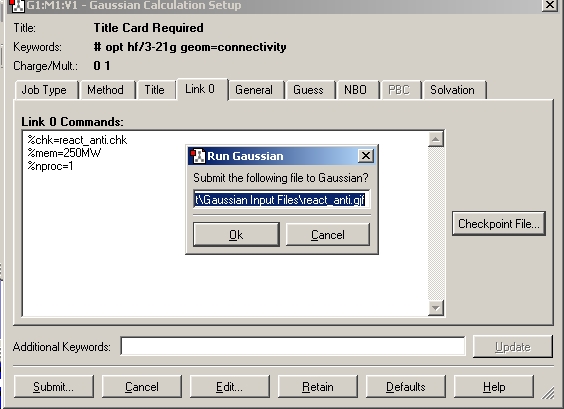
A Gaussian calculation was then set up to optimise the structure using the Hartree Fock method and 3-21G basis set, as shown below.

Initially when this was submitted the following error message appeared:

Examining the calculation setup revealed that the link 0 tab had %mem=250MW instead of %mem=250MB written in the second line. Changing this fixed the problem.

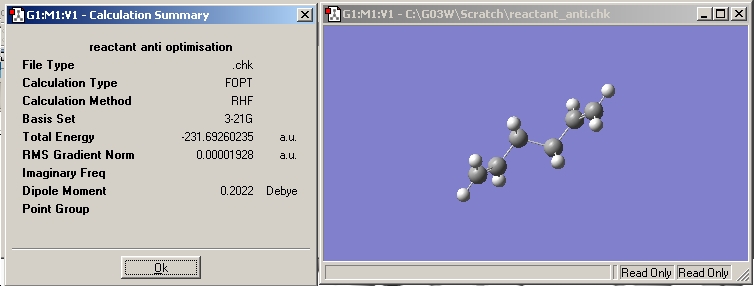
The fchk file was opened and the results summary viewed. This can be seen below. The energy is -231.69260235 Hartree or -608309 KJ/mol (as 1 Hartree = 2625.5 KJ/mol and the error in the calculations is approximately 1`KJ/mol) or -0.3692 kcal.mol (as 1 Hartree = 627.5095 kcal/mol).

Obtained geometry from anti calculation

Selecting Symmetrise under the edit tab gave a C2 point group.

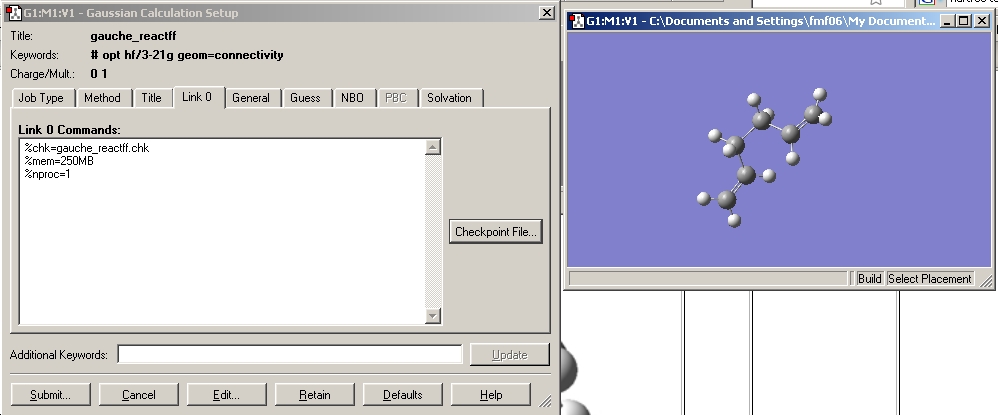
The same procedure was followed for 1,5-hexadiene with a gauche linkage. Considering the energy level diagram below and the sizes of the substituents on C2-C3, I would expect the gauche conformer to have a larger energy than the anti conformer due to more torsional strain and steric repulsion between the two C2H3 groups on the C2 and C3 carbons occuring when they are gauche as a pose to antiperiplanar. Conformational Energy Diagram for Ethane

The calculation setup is shown below.

The resulting fchk file was opened and the results summary viewed. This can be seen below. The energy is -231.69266122 Hartree or -608309 KJ/mol (as 1 Hartree = 2625.5 KJ/mol and the error in the calculations is approximately 1`KJ/mol) or -0.3692 kcal.mol (as 1 Hartree = 627.5095 kcal/mol).

Obtained geometry from gauche calculation

The reported symmetry was C1. Comparing the energy and symmetry to those in Appendix 1 reveals that the gauche3 conformer was found, and this is slightly lower in energy than the anti1 conformer found in the previous calculation (contrary to my prediction) . This can be ratonalised by the posibility of a stabilisation resulting from the overlap of the orbitals in the two double bonds as in this orientation they are close in space. This is of course balanced by repulsive steric interactions to give the gauche3 the lowest energy. In order to see if this was correct the MO's were visualised in gaussian and the HOMO revealed that the two doubly bonded carbons pi orbitals did interact, resulting in a favourable interaction between them that lowers the energy of the gauche conformation. I would predict these two structures to be the lowest energy conformers as they minimise the steric repulsions. Examining the table in Appendix 1 shows this to be the case. However the energy difference between the two conformers is low, compared to RT (which is 2.479KJ/mol = 0.592Kcal/mol ). The anti1, anti2 and gauche3 can all interconvert readily ar room temperature as their relative energies are smaller than this value.

The C_i symmetry anti conformer was drawn in gaussview and the structure optimised as done previously. This molecule is not the lowest energy conformation but is thought to be the most reactive species. As its energy is still low a certain amount will be present in solution (according to the boltzmann distribution). As this is used up the conformation of other 1,5-hexadiene molecules will shift to maintain the equilibrium population of states. This is the molecule which I will use as the reacting species when calculating the activation energy of the cope rearrangement.

The results summary of the calculation was viewed and is shown below.

Ci conformer

The energy was -231.69253506 Hartree or -608309 KJ/mol. This is in accord with that shown for the anti2 conformer shown in Appendix 1.

Examination of the symmetry revealed it to be Ci.

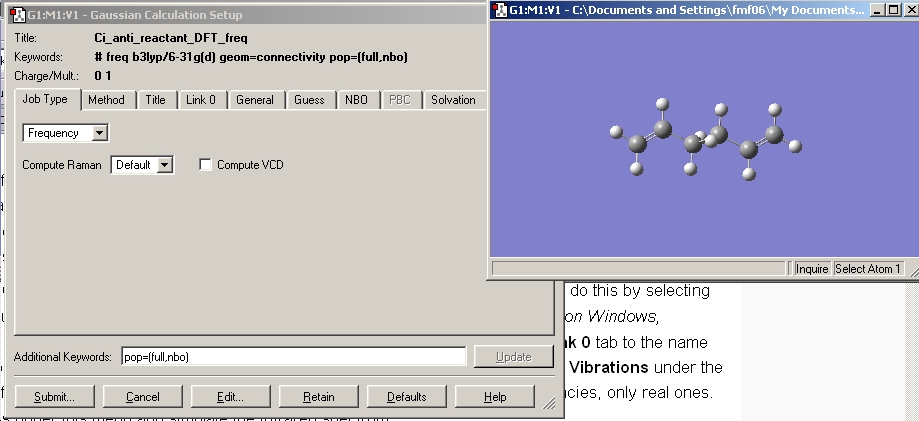
This file was then re-saved under a different name and a DFT calculation run using the B3 LYP method and the 6-31G(d) basis set. In order to ensure the point group remains the same the point group was constrained to Ci as shown.

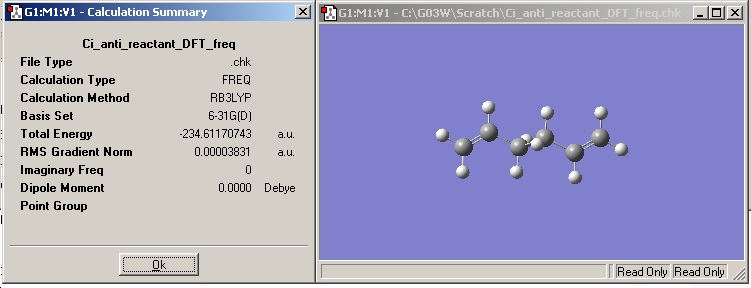
The checkpoint file was opened and the results summary shown below.

The energy was -234.61170743 Hartree or -615973 KJ/mol.

Structure obtained from DFT optimisation

Comparison of geometries and energies

Energy

The energy obtained is 2.91917 Hartree or 7664 KJ/mol lower energy than that obtained from hartree fock 3-21G calculations. This is a significant difference but can be accounted for by the fact that the energies given by different methods cannot usually be compared due to diferent approximations in each method.

Point Group

The point group remained the same (Ci) as the molecule cannot break symmetry during a gaussian optimisation (as demonstrated in Module 2 for NH3).

(NB the calculation was also run without constraining the point group symmetry and the same energy and point group were obtained).

Bond angles and lengths

The length of the C1=C2 bond was 3.32 amstrongs in the HF/3-21G calculation compared to 3.33 amstrongs in the DFT B3LYP calculation.

The length of the C3-C2 bond was 1.51 amstrongs in the HF/3-21G calculation compared to 1.50 amstrongs in the DFT B3LYP calculation.

The C2-C3-C4 angle is 111 degrees in the HF calculation vs 113 degrees in the DFT. This is the only significant difference. Assumably widening this angle reduces the steric interaction between the two alkene groups and results in a lower energy.

The C2-C3-C4-C5 dihedral angle is -180 degrees in both structures in accord with the Ci point group.

Hence although the point group has remained the same the structure has changed slightly upon DFT B3LYP optimisation. The reason for carrying out low level pre-optimisations before doing accurate calculations is thus shown; the low level calculation optimises the molecule to almost the same geometry as the higher level one, but is much faster. Hence using a pre-optimised structure as the input file for a higher level calculation will speed it up as the molecule is already almost in it's lowest energy conformation.

Frequency Calculation

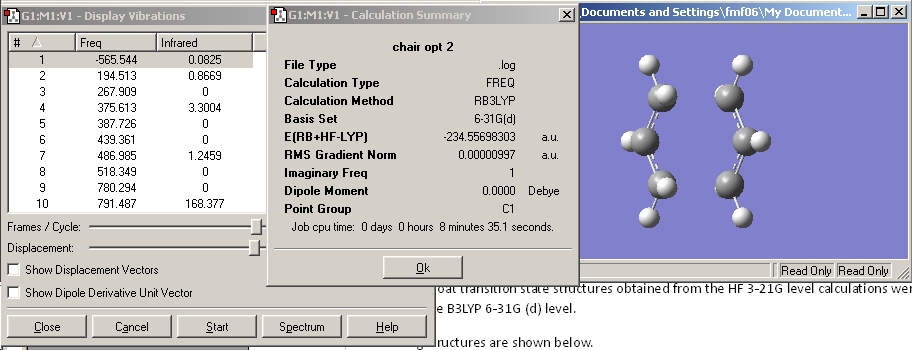
The frequency calculation was set up starting from the DFT, 6-31G(d) optimised structure, at the same level of theory, as shown below.

This was run and the results summary viewed. This can be seen below.

Note that the energy obtained for this calculation is the same as that obtained for the optimisation calculation.

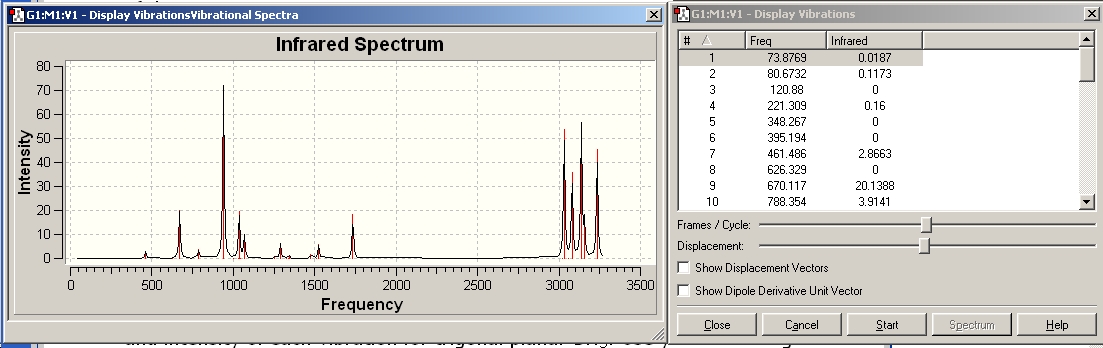
The vibrations were viewed and the spectrum is shown below.

The frequencies (some of which can be seen on the right in the screenshot above) were all examined and no negative frequencies were found. Hence the optimisation has found the minimum on the potential energy surface.

The log file was viewed and the energies obtained are shown in the table below. The calculation was re-run using the additional keywords 'Freq=ReadIsotopes' and then adding the following to the end of the input file to specify 0k temperature and 1 atmosphere pressure (default). (blank line) 0.0 1.0 However this resulted in the exact same energies as the calculation returned to the default temperature and so effectively I just re-ran the same calculation as before. Consulting the Gaussian online manual revealed that the correct keyword to use in this case is 'temperature=...'. This was input so the first line of the logfile read;

# freq b3lyp/6-31g(d) pop=nbo geom=connectivity temperature=0.001

A low temperature was used as a pose to 0K as 0 in temperature returned the default 298.15K calculation again.

This returned the results shown below. All energies are the same (the zero point energy) as at (or very close to) 0K there is no thermal energy and entropy=0.

Energy term	at 298.15 K	at 0.001k
Sum of electronic and zero-point Energies	-234.469201	-234.468781
Sum of electronic and thermal Energies	-234.461855	-234.468781
Sum of electronic and thermal Enthalpies	-234.460906	-234.46871
Sum of electronic and thermal Free Energies	-234.500781	-234.468781

The units are in Hartrees.

The same calculation was set up for the HF 3-21G optimised structure at this level of theory and the energies obtained from the logfile are shown below:

Sum of electronic and zero-point Energies	-231.539542
Sum of electronic and thermal Energies	-231.532571
Sum of electronic and thermal Enthalpies	-231.531627
Sum of electronic and thermal Free Energies	-231.570899

Optimising the Chair and Boat Transition Structures

Optimising the Chair and Boat transition structures

Firstly the allyl fragment CH2CHCH2 was drawn in Gaussview and optimised to the HF/3-21G level of theory. The setup is shown below.

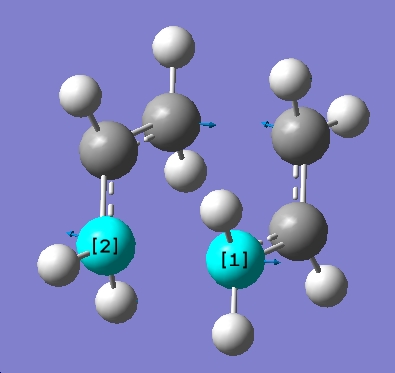
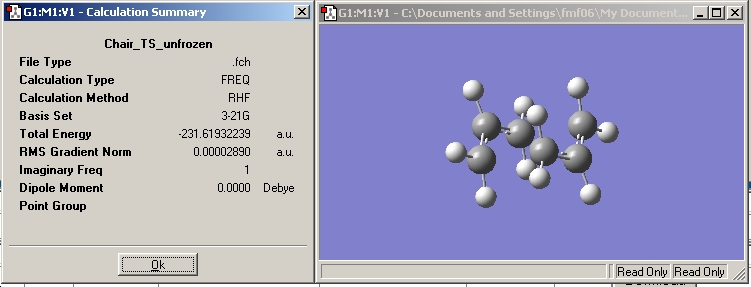
Chair Transition State

The first transition state to be modelled is the chair form.

This was then pasted twice into a new window and the fragments arranged in the chair conformation, as shown in the Appendix 2. The fragments were positioned 2.2 amstrongs apart as shown below and the file saved.

Method 1

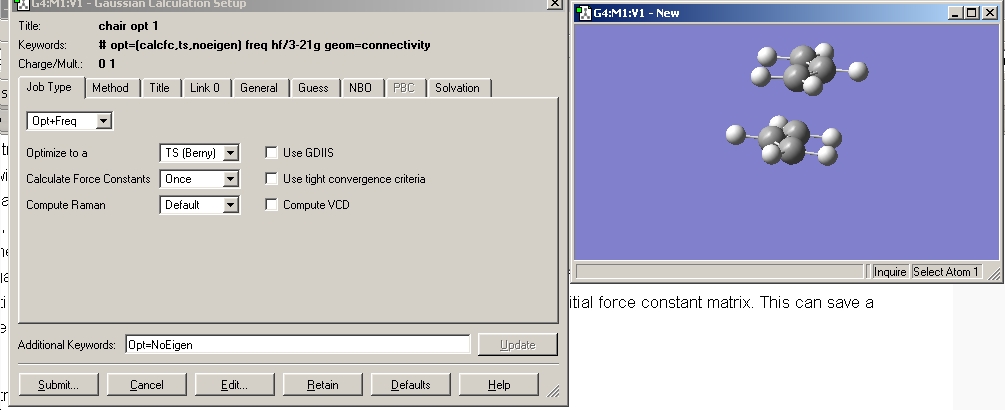
This was then copied to a new window and a optimisation and frequency calculation set up as shown below and run.

The results file was opened

The output file was opened and the spectra viewed. These are shown below.

The resultant structure and some of the vibrations can be seen below

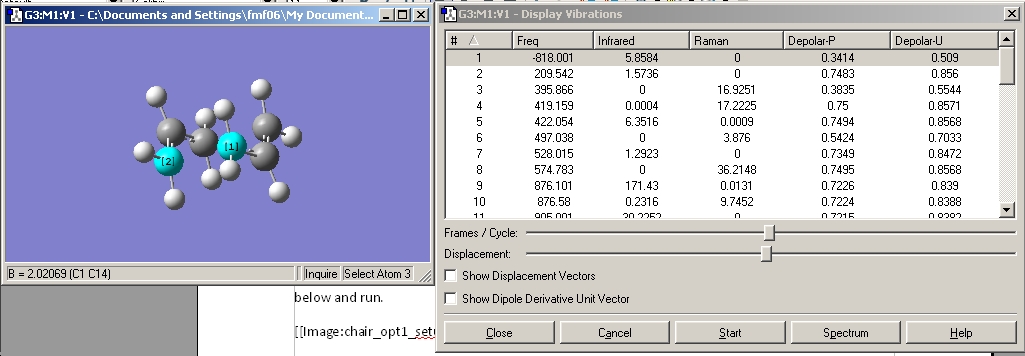
These were checked for negative frequencies and one of these occurred at -818 cm-1. This was visiualised and found to correspond to the one corresponding to the cope rearrangement, as shown below.

Vibration

This is in accord with what should be seen.

The distance between the two fragments was found to be 2.02 amstrongs.

The calculation can be found on D-space at:http://hdl.handle.net/10042/to-2077

Method 2 – frozen co-ordinate method

A new calculation was run on the chair fragment (unoptimised).

This time the distences between the two fragments was frozen to 2.2 amstrongs using the redundant co-ordinate editor and the calculation run as an optimisation using the HF 3-21G method. The calculation setup is shown below.

The results summary was viewed. Note that the energy is higher than that found by Method 1, this is as the fixed bond lengths have not yet been optimised and are still 2.2 amstrongs.

The resulting structure can be viewed below.

The relevant bond lengths were then un-frozen using the redundant co-ordinate editor and an opt+freq calculation run.

The .chk file was open and the results file viewed. This can be seen below.

The resulting structure displayed one imaginary vibration at -818cm-1

This corresponded to the cope rearrancement reaction mechanism, as shown below:

The calculation can be found on D-space at:http://hdl.handle.net/10042/to-2078

Comparison of Structures

	Method 1	Method 2
C1-C6 bond length	2.02	2.02
C3-C4 bond length	2.02	2.02
C1-C2 bond length	1.39	1.39
C2-C3 bond length	1.39	1.39
Energy in Hartree	-231.69132244	-231.69132239

The two structures are very similar and have very simiar energies ane vibrational frequencies. Hence either method can be used to calculate the transition state in this case.

Boat Transition State

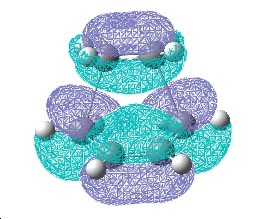
The boat structure transition state is shown below.

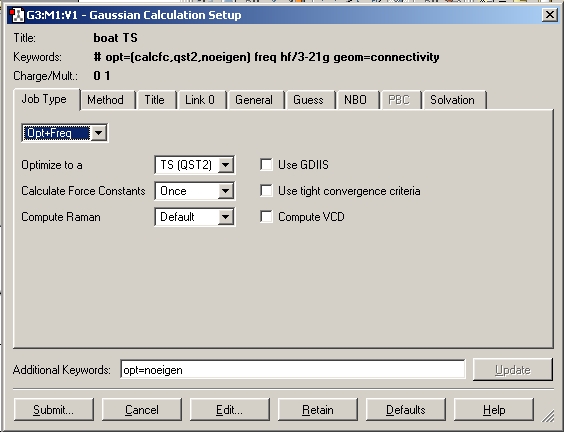
This will be modelled by specifying reactants and products. This was done by using the 'Add to molgroup' feature.

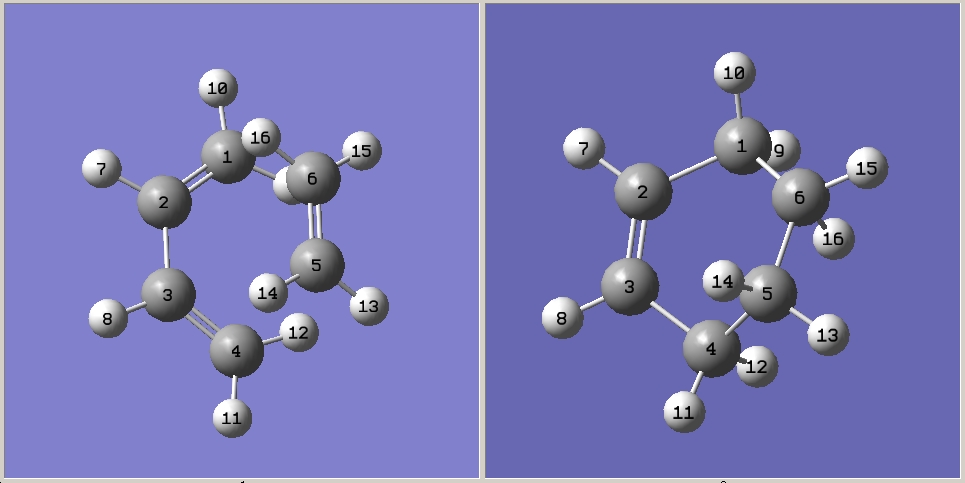
The numbering was manually changed using the atom editor so that the input file looked like that shown in the feature below.

Set up calculation as shown

The calculation failed. The chk file was opened and the resulting transition state was found to be that shown below. The calculation has translated the top allyl fragment as a pose to rotated about the bonds.

In order to get a result from the file the input file was modified to be closer to the boat structure.

The input file geometry is shown below.

The calculation was re-run and the resulting transition state was now a boat structure. This can be seen below.

The results file was viewed and the vibrations checked to ensure there was one negative frequencey. This occurred at -841 cm-1 .

This negative frequency corresponded to the reaction mechanism of the cope rearrangement, as shown below:

Vibration

This can be found on D-space at:http://hdl.handle.net/10042/to-2047

Following the reaction mechanism

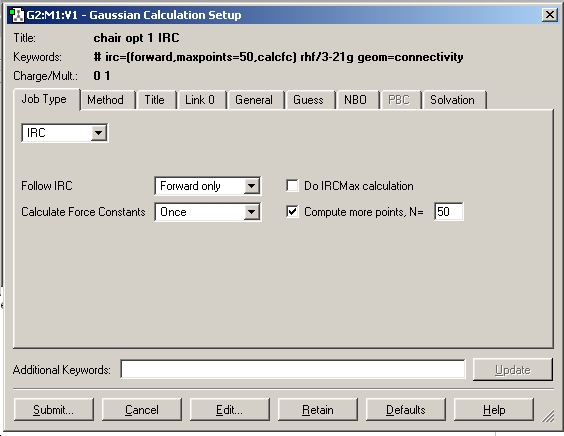
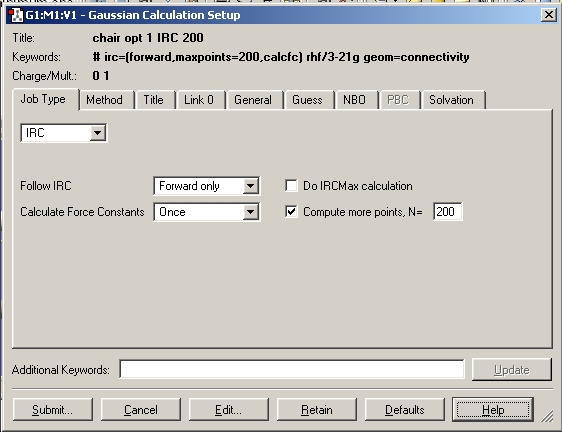
The checkpoint file for the TS(berney) optimised chair transition state was opened and the IRC calculation set up as shown below.

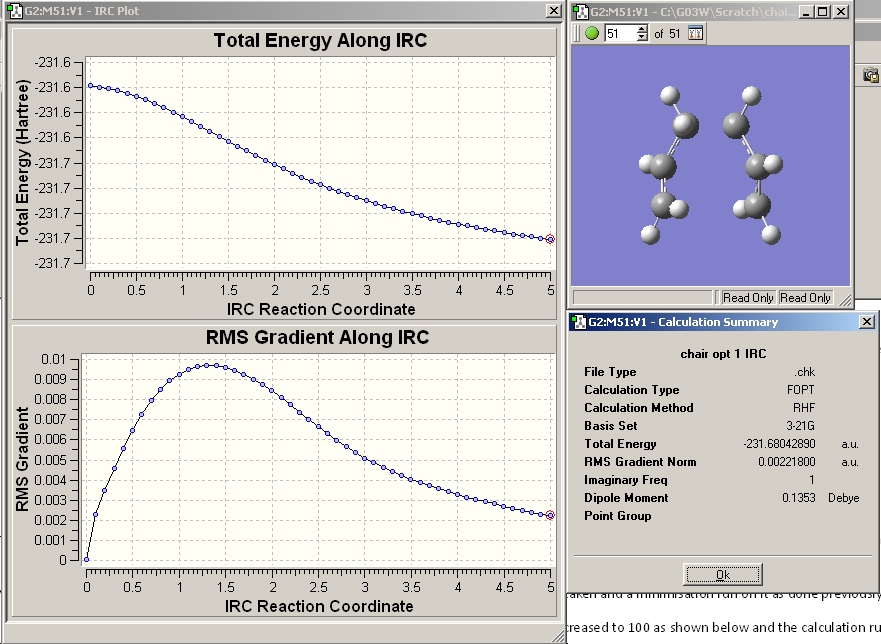
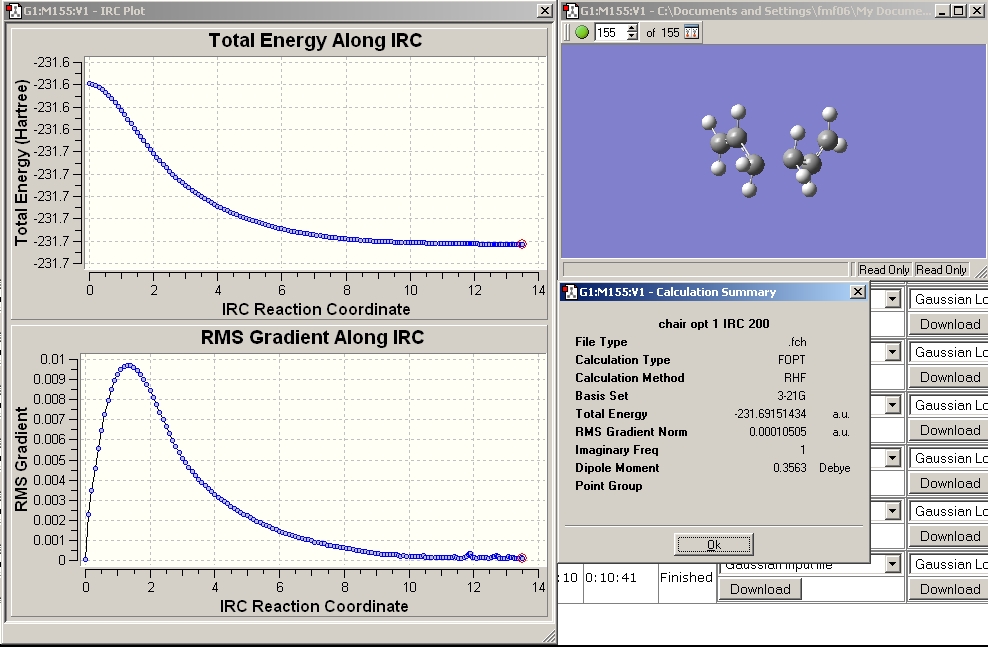
After the calculation had finished the output file was opened in gaussview.

Examination of the RMS gradient showed it was not smaller than 0.001. Examining the graph of the energy and the RMS gradient and comparing the energy of the final structure to that of the low energy conformers in appendix1 lead me to conclude that the calculation hadn't reached a minimum yet. In order to find the minimum three calculations were run.

i)

The last point in the IRC was taken and a minimisation run on it as done previously

The structure was optimised to a minimum energy to the HF/3-21G level. This calculation can be found on D-space at:http://hdl.handle.net/10042/to-2048

The resulting structure is shown below. The RMS gradient is smaller than 0.001 indicating the calculation converged.

This energy and the C2 symmetry correspond to the gauche 2 conformation found in Appendix 1.

ii)

The number of points was increased to 200 as shown below and the calculation run again until a minimum was reached.

The chk file was opened and the IRC and results summary viewed.

The calculation can be found on D-space at:http://hdl.handle.net/10042/to-2049

This structure is also of C2 symmetry but is of a slightly higher energy than the one obtained in part i)

The C1-C2-C3-C4 dihedral angle and the C1-C2-C3 angle has decreased making this structure closer to that of the gauche4 conformer found in Appendix1. The energy also corresponds best to this.

Note that the calculation had to compute155 points before it reached a minimum (hence why when a calculation to compute 100 points (run before this one) did not reach a minimum). This is very computationally expensive and time consuming – the calculation took over 4 hours! This is a limitation of this method.

Comparison of methods

Method	i)	ii)
Energy	-231.69166702	-231.69151434
C1-C2-C3 Angle	125.0	125.1
C1-C2-C3-C4 Dihedral	123.9	117.0
Corresponding product structure	Gauche 2	Gauche 4
Time taken	10minutes and 9 seconds	4 hours, 58 minutes and 30seconds

As can be seen in the table above the two methods gave different structures. Method ii) is more reliable than method i) and hence the structure obtained by it is more likely to be accurate. However gauche 2 and gauche 4 conformers are similar and hence there is not a huge difference between the two methods. The big disadvantage of using the more accurate method ii) is that it is much much more computatuionaly demanding and time consuming!

Activation Energies

Optimising the transition states

The chair and boat transition state structures obtained from the HF 3-21G level calculations were optimised to the B3LYP 6-31G (d) level. The first line of the input file read:

# opt=(calcfc,ts) freq rb3lyp/6-31g(d) geom=connectivity

The resulting structures are shown below.

Chair

Found on D-space at:http://hdl.handle.net/10042/to-2046

Boat

Found on D-space at:http://hdl.handle.net/10042/to-2047

Comparisons of methods

Numbering system

Geometry of boat

	HF/3-21G	B3LYP/6-31G*
C1-C2 length	1.38	1.39
C3-C4 length	2.14	2.21
C1-C2-C3-C4 dihedral angle	-64.8	-64.2
C2-C3-C4-C5 dihedral angle	0.0	0.0

Geometry of chair

	HF/3-21G	B3LYP/6-31G*
C1-C2 length	1.39	1.41
C3-C4 length	2.02	1.97
C1-C2-C3-C4 dihedral angle	68.5	68.2
C2-C3-C4-C5 dihedral angle	-54.9	-54.0

As can be seen from the two tables above the geometry has changed very little upon re-optimising to the higher B3LYP/6-31G* level with bond lengths differing by less than 0.05 amstrongs. Hence running a fast, low level pre-optimisation prior to a high level one is advisable as this optimises the molecule to a structure very close to the one that will be obtained from the higher level calculation and hence reduces the time and computational demand of the calculation.

Energies

These energies were found to be in accord with those found in Appendix 2

Level	HF/3-21G	HF/3-21G	HF/3-21G	DFT/B3LYP/6-31G*	DFT/B3LYP/6-31G*	DFT/B3LYP/6-31G*
Structure	Electronic energy	Sum of electronic and zero-point energies at 0K	Sum of electronic and thermal energies at 298.15 K	Electronic energy	Sum of electronic and zero-point energies at 0K	Sum of electronic and thermal energies at 298.15 K
Anti 2 reactant	-231.692535	-231.539542	-231.532571	-234.61170743	-234.469201	-234.461855
Boat TS	-234.54309307	-231.450921	-231.445295	-234.54309307	-234.402342	-234.396008
Chair TS	-231.619322	-231.466702	-231.461342	-234.556983	-234.414930	-234.409009

The table above shows that the energies obtained for the different methods are significantly different. This is due to having used a larger basis set for the DFT B3LYP calculations and due to different approximations being made by the two different methods. Below is a discussion of some of the reasons the two differ, (as found in Module 1 of this course).

Hartree Fock is a semi-empirical method that uses a LCAO approach, using gaussian type functions (of the form -ar2) to describe the wavefunctions . In this case a small basis set was used meaning some core electrons have been emitted from the calculation. Some two electron repulsion terms are also omitted in this method. This gives rise to errors which are corrected for by introducing parameters to correlate results to those obtained experimentally or by using ab initio methods which do not omit any terms. The solutions obtained from the schrodinger equation are then minimised using variational techniques. The energy obtained will always be higher than the real energy (according to the variational theorum). The limiting smallest value to which the calculations converge is known as the Hartree- Fock limit.

One of the limitations of the HF calculation method is that it calculates the average effect of electron repulsion but doesnt calculate/account for explicit interaction between individual electrons (electron correlation). The approximations used are summarised below, these are the major causes of error/inaccuracy in the calculations.

1. The Born Oppenheimer approximation

2. Omitting core electrons (incomplete basis set)

3. Central Field approximation (incomplete correlation)

4. The omission of relativistic effects

Density functional calculations give more accurate results than semi-empirical ones do (although they take longer and are have higher computational requirements).

The main difference in DF calculations is that they compute the energy of the molecule from the electron density and not from the wavefunction. So rather than forming a linear combination of atomic orbitals to find the wavefunction, a linear combination of basis functions is used to find the electron density (Kohn-Shan orbitals). This expression is then put into a determinant and the electron density obtained from this is used in subsequent calculations (put into density functionals, in this case B3LYP to find the energy.

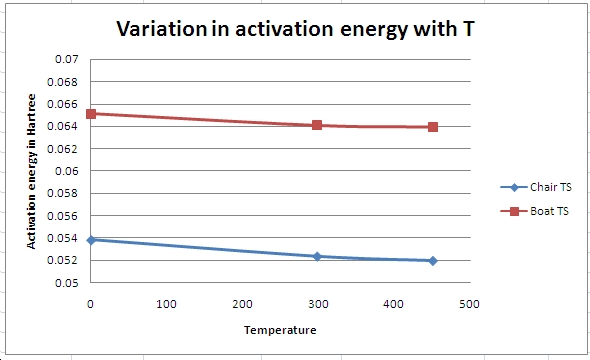
The energies at different T and 1 atmosphere were also obtained for the DFT optimised structures (important as can only compare within the same calculation method) using the FreqChk program and entering 1 (for 1K), 0 (for default, 298.15K) and also 450 (for 450.00K) when prompted by the line “Temperature (K)? [0=>298.15]” The results were plotted on an excel spreadsheet and can be seen below.

As shown above the energies of the reactant and transition states get closer and hence activation energies get smaller as temperature is increased, but the boat transition state remains higher energy than the chair. They show the expected trend, i.e. that the reaction can be thermally activated.

Activation energies

The energies of the reactant and transition states were converted to kcal/mol using the relation 1 hartree = 627.509 kcal/mol and the activation energies calculated.

	HF/3-21-G 298.15K	DFT/B3LYP/6-31G* 298.15K	HF/3-21-G 0K	DFT/B3LYP/6-31G* 0K	Experiment 0K
Activation energy Chair	44.69	33.17	45.70	31.06	33.5 ± 0.5
Activiation energy Boat	74.76	41.32	55.60	41.96	44.7 ± 2.0

As can be seen the activation energies that correspond best to those found experimentally are those calculated at the DFT B3LYP/6-31G level at 298.15 K . This is in agreement with what is expected when the level of calculation is taken into account. The boat transition structure is, in all cases, found to be of a higher energy than the chair. This makes intuitive sense as the steric strain in the boat transition structure is larger than in the chair. The activation energies for the boat transition state are higher and hence the preferred mechanism is via a chair transition state, which links the Ci anti conformer to the gauche 2 or gauche 4 conformer. The experimental value is given at 0K but examination of the literature revealed the actual experimentally derived activation energy to be valid at 298.15K and hence the results agree very accurately with the experimental values.

The results at 450K show a very small activiation energy in comparison and this shows that the reaction can be thermally activated and will proceed faster when heated. This is in accord with the pericyclic selection rules that state a 4n+2 reaction will occur via a huckel aromatic transition state under thermal conditions.

The Diels Alder Cycloaddition

Cis Butadiene and Ethene

The reaction of cis butadiene with ethylene is a [4+2] cycloaddition. This is thermally allowed by the pericyclic selection rules as it involves 6 pi electrons. It should therefore proceed via a Huckel transition state will all suprafacial components.

Optimisation of Cis Butadiene

Cis butadiene was drawn in GaussView and it's geometry optimised first to the HF 3-21G level and then optimised to the DFT 6-31G(d) level. The frequencies were computed at the same time to ensure that the calculation had reached a minimum.

The first lines of the input files are shown below.

HF 3-21G : # opt freq hf/3-21g geom=connectivity

The resulting structure was planar and of C2v symmetry.

Found on D-space at:http://hdl.handle.net/10042/to-2057

DFT B3LYP/6-31G* : # opt freq rb3lyp/6-31g(d) geom=connectivity

Found on D-space at:http://hdl.handle.net/10042/to-2058

The resulting fully optimised structure can be loaded below:

The molecular orbitals were then computed using the AM1 method. The calculation set up is shown below:

Note the keyword”pop=full” to turn on MO analysis.

The MO calculation can be found on D-space at:http://hdl.handle.net/10042/to-2059

Ethene was also optimised to the B3LYP 6-31G* level and the MO's computed.

This calculation can be found on D-space at:http://hdl.handle.net/10042/to-2064

The MO calculation can be found on D-space at:

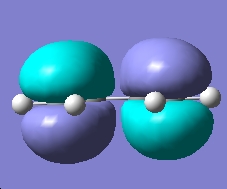
The HOMO of cis-butadiene is plotted below and has an energy of -0.343 Hartree

The symmetry of the HOMO with respect to the reflection plane of the molecule is antisymmetric.

The LUMO of ethene is plotted below and has an energy of 0.051 Hartree

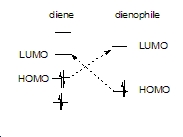
The symmetry of the LUMO of ethylene is also antisymmetric so these two orbitals can interact.

The LUMO of cis-butadiene is plotted below and has an energy of 0.017 Hartree

The symmetry of the LUMO with respect to the reflection plane of the molecule is symmetric.

The HOMO of ethene is plotted below and has an energy of -0.387 Hartree

The HOMO of ethylene is also symmetric with respect to the reflection plane so these two orbitals can interact.

Computing the transition state geometry

Method 1

The transition state was optimised using the QST2 method.

The starting materials and products in the input file were drawn and labelled as shown below.

This was then optimised, the first line of the input file read:

# opt=(qst2,noeigen) freq hf/3-21g geom=connectivity

Note the 'opt=NoEigen' addtiional keyword is to stop the calculation crashing if more than one imaginary frequency is detected during the optimization.

The .fchk file was opened and the vibrations examined. It was found that the transition state displayed one imaginary frequency at that corresponded to a concerted reaction mechanism where the two sigma bonds in the product form simultaneously and the three double bonds breaking stretch. The single bond that is forming a double bond is shortened in this vibration. Hence the computed imaginary vibration of the transition state corresponds to a pericyclic mechanism.

The calculation can be found on D-space at:http://hdl.handle.net/10042/to-2061

Vibration

The energy was found to be -231.60320842 Hartree.

This structure was then re-optimised to the DFT B3LYP/6-31G* level.

The first line of the input file is shown below.

# opt=(calcfc,ts,noeigen) freq rb3lyp/6-31g(d) geom=connectivity

This calculation can be found on D-space at: http://hdl.handle.net/10042/to-2062

The .fchk file was opened and the vibrations viewed. The negative frequency corresponding to the reaction mechanism was this time at -525 cm-1 and is animated below. The energy was found to be -234.54389648. This is lower and significantly different to that obtained from the lower level HF/3-21G calculation even though the geometry has not changed much, for reasons described in the Cope rearrangement tutorial section.

Frequencies

The negative frequency can be viewed below and clearly shows that the two sigma bonds are formed simultaneously (concerted mechanism). The lowest positive frequency corresponds to the ethene fragment rocking across the top of the cis-butadiene fragment. This vibration does not correspond to any bond forming or breaking and is not an imaginary vibration so this makes sense.

	Negative ferquency	Lowest positive frequency
Wavenumber (cm-1)	-525	136
Image
Jmol	Vibration	Vibration

Resultant geometry

	TS optimisation results B3LYP/6-31 G*	HF/3-12G	Literature HF/3-12G
Jmol
Image
Bond lengths C1-C6/ C4-C5 (amstrongs)	2.27	2.21	2.2-2.3
Bond length C1-C2/ C3-C4 (amstrongs)	1.38	1.37	1.37
Bond lengths C5-C6 (amstrongs)	1.39	1.39	1.39
Bond length C2-C3 (amstrongs)	1.41	1.40	1.40
Covalent radius Carbon amstrongs)	0.77
Typical C-C bond length (amstrongs)	1.54
Typical C=C bond length (amstrongs)	1.35
Typical sp2-sp3 C-C bond length	1.50

Literature data from table

Bond lengths from Fox, MA and JK Whitesell. Organische Chemie. 1994. Spektrum.

Covalent radius of carbon from Covalent radii of carbon and the conjugation problem,Russian Chemical Bulletin, Springer New York, 1066-5285 (Print), Volume 9, Number 8 / August, 1960.

The literature data for the HF/3-21G calulation is from the paper C. Spino, M. Pesant and Y. Dory, Angew. Chem. Int. Ed. Engl., 37, 3262 (1998).

Discussion The HF/3-21G calculation results exactly matched those found in literature implying that the calculations ran sucessfully. As can be seen from examination of the table above, the bond length of the forming C-C sigma bonds is larger than a typical C-C bond length as these have not fully formed yet. The C1-C2 and C3-C4 bonds go from being double in the reactant to single in the product. In the transition state they are closer to double than they are to single implying that the transition state resembles the reactants more than the products (early transition state). The C2-C3 bond goes from being single to double and is longer in the transition state than the C1-C2 bonds further backing up this idea. The C5-C6 bond goes from double to single and in the transition state is closer in length to a double bond. These results show that in the transition state the bonds form/break in a concerted manner but the bond lengths are not uniform around the system. The covalent radius of SP3 carbon shows that all bonds of length smaller than 1.54 amstrongs have a bond order of larger than 1. (i.e. all bonds except the forming sigma bonds which have a bond order less than 1).

Computing the MO's

The MO's were then computed on the DFT B3LYP 6-31G* optimised transition state.

The first line of the input file read:

# opt=(calcfc,ts) ram1 geom=connectivity pop=full

This calculation can be found on D-space at:http://hdl.handle.net/10042/to-2063

The MO's can be seen below:

	HOMO-1 (MO 16)	HOMO (MO 17)	LUMO (MO 18)
Orbital
Energy	-0.325	-0.323	0.023
Symmetry with respect to the plane	Symmetric	Antismmetric	Symmetric
Orbitals comprised of	HOMO butadiene and LUMO ethene*	LUMO butadiene and HOMO ethylene	HOMO butadiene and LUMO ethene

*The HOMO-1 also looks like it could feasibly be comprised of the HOMO-2 of cis-butadiene (fully delocalised pi bonding orbital across the entire structure) and the HOMO of ethene. The HOMO-2 of cis-butadiene has an energy of -441 Hartree so this is closer in energy to the HOMO of ethene and they are both of the same symmetry so this mixing of orbitals is also is feasible.

As can be seen in the table above the HOMO is bonding between C1 and C6 and C1 and C5 (dorming sigma bonds) wheras the HOMO-1 and the LUMO have a nodal plane between these atoms (and are thus antibonding in this area). The HOMO and HOMO-1 are close in energy, but of different symmetries.

The MO calculation was then re-run on the B3LYP/6-31g* optimised transition state model to the MP2 level.

The first line of the input file is shown below.

#opt=(calcfc,ts) freq rmp2 geom=connectivity pop=full

This can be found on D-space at:http://hdl.handle.net/10042/to-2069

The MO's were viewed and the results are shown below.

	HOMO-1 (MO 22)	HOMO (MO 23)	LUMO (MO 24)
Orbital
Energy	0.249	-0.240	-0.242
Symmetry with respect to the plane	Antiymmetric	Symmetric	Symmetric
Orbitals comprised of	HOMO butadiene and LUMO ethene	LUMO butadiene and HOMO ethene*	LUMO butadiene and HOMO ethene*

Negative vibration frequency	-839.51
Energy of TS	-230.41189092 Hartree
Bond lengths C1-C6/ C4-C5 (amstrongs)	2.24
Bond length C1-C2/ C3-C4 (amstrongs)	1.39
Bond lengths C5-C6 (amstrongs)	1.39
Bond length C2-C3 (amstrongs)	1.45

From the table above it is clear that the HOMO now has a nodal plane between the C1-C6 and C4-C5 and the distance between these carbons has lengthened. However the HOMO-1 is filled and it has a bonding interaction between these atoms in this MO, examination of other lower MO's also showed bonding character in this region. Hence bonding interactions in lower orbitals that the HOMO mean there is still net bonding between them.

Comparison

In the AM1 method the HOMO was MO17 and the LUMO was MO 18 wheras in the MP2 level calculation the HOMO was MO 23 and the LUMO was MO 24. This is as the AM1 method has excluded some core electrons in the calculation wheras the MP2 has computed MO's for them.

The MP2 method gives a structure in which the distance between carbons forming double bonds from single and those forming single bonds from double are the same (i.e. the transition state is midway between the product and the reactant) wheras the AM1 predicts an early transition state.

Both calculations give the HOMO and HOMO-1 similar energies relative to each other (energies are not comparable between methods due to different approximations made in the calculations). However the two methods give the HOMO and HOMO-1 in different orders. The MP2 level calculation is more likely to represent the real transition state as this calculation is much more accurate than AM1. Both imply a bonding interaction is occurring between C1-C6 and C4-C5 which is in agreement with the reaction mechanism.

Reason the reaction is allowed

This reaction is allowed as it obays the pericyclic selection rules. It involves 4 pi electrons from the cis-butadiene and 2 pi electrons from the ethene making it a 6 electron process [i.e. a 2n+2 where n=2]. The pericyclic selection rules state that this reaction will proceed under thermal activation (as a pose to photochemical).

The Woodward-Hoffman selection rules state that this must go via all suprafacial components. Examination of the topology of the transition state MO's and the frontier molecular orbitals in the reactants shows this to be the case. Both bonds are formed on the same face of the diene via a concerted mechanism. The orbitals which mix to give the MO's in the product are of similar energies and the same symmetry hence mixing is allowed. The orbital correlation diagram below shows this.

Orbital correlation diagram

Online example

A very nice simulation of how the MO's of the reactants change into those of the transition state along the reaction co-ordinate of a diels alder reaction can be viewed here: http://www.springer.com/carey-sundberg/dielsalder/dielsalder.php. (Scroll down and follow link, popups must be enabled). Or alternately try the direct link (doesn't always load) : http://www.springer.com/carey-sundberg/dielsalder/views/damoall.html.

To Study the regioselectivity of the Diels Alder Reaction

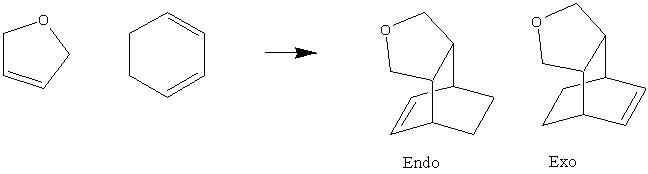
The reported selectivity of the diels alder reaction is to be investigated by calculating the transition states (along with products and ractants) for the endo and exo products in order to rationalise the predominance of the endo product.

Optimising the transition states

The transition states for the endo and exo forms were then modelled by creating a guess structure in Gaussview as shown in the picture below. This was done by using the frozen co-ordinate method.

The distances between the two sets of carbons forming sigma bonds to each other were frozen at 2.2 amstrongs and the structure optimised to a minimum at the Hartree Fock/3-21G level. The first line of the input file was:

# opt=(calcfc,modredundant) freq hf/3-21g geom=connectivity

This was then optimised to a TS(berney) to the same level but without calculating the force constants (this was set to Never). The first line of the input file was:

# opt=(ts,modredundant,noeigen) freq rhf/3-21g geom=connectivity

Guess endo TS input

Guess exo TS input

Starting from the HF optimised structure the transition state was then optimised by the same method to the higher DFT B3LYP/6-31G* level.

The first line of the input files are shown below:

# opt=(calcfc,modredundant,noeigen) freq rb3lyp/6-31g(d) geom=connectivity

# opt=(ts, calcfc, noeigen) freq rb3lyp/6-31g(d) geom=connectivity

The two optimisation geometries were compared and it was found that, like in previous calculations, the DFT B3LYP/6-31G* gave a slightly looser transition state structure with slightliy longer bond lengths, but that the overall geomtries and MO's were very similar. The B3LYP 6/31G* calculations can be considered more acurate as discussed previously and so these are the ones I have based my analysis on.

The HF 3-21G optimised transition states can be found on D-space:

Endo :http://hdl.handle.net/10042/to-2075

Exo:http://hdl.handle.net/10042/to-2073

The resulting DFT B3LYP/6-31G* optimised transition state geometries can be loaded below.

Endo Transition State

D-space link:

Exo Transition State

D-space link:

Imaginary Vibrations

Both files were checked to ensure they had an imaginary vibration, which they did confirming a transition state had been calculated.

Transition State	Endo	Exo
Vibration	Vibration	Vibration
Snapshot
Imaginary Frequency (cm-1)	-447	-449

As can be seen above the two have similar imaginary frequencies that correspond to concerted formation of the two sigma bonds in the product and lengthening of the pi bonds (that break), confirming that the reaction is in fact a pericyclic cycloaddition reaction.

Geometries

Assume for the numbering in the other form that the double bonds move (so different numbered C's are double bonded) but the atoms stay in the same places.

Transition State	Endo	Exo
C-C sigma bond length (amstrongs)	2.27	2.29
C11-C14/C12-C16 length (amstrongs)	2.99	3.03
Closest H on C14 and C11 distance	3.14	2.53
Dihedral C11-C6-C2-C14 (degrees)	54.8	48.8

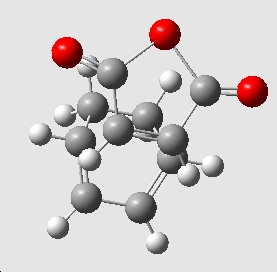
The optimised transition states reveal that the exo transition state lies at a point where the O=C-O-C=O fragment of the maleic anhydride is significantly further from C14-C16 than in the endo transition state. As a result of this the length of the forming C-C sigma bonds is longer in the exo transition state.

This can be rationalised by examination of the distances between the C's in the O=C-O-C=O fragment of the maleic anhydride and the closest H's on the C14-C16. In the exo form the C14 and C16 are singly bonded to each other (and sp3 hybridised) and have two attached H's. The distance between the 'top' H and the maleic anhydride fragment is significantly shorter in the exo form, despite the maleic anhydride being further away. In the endo form the C14 and C16 are doubly bonded and sp2 hybridised. Thus they each only have one H attached and this likes in the plane of the molecule. Hence the steric repulsion is much less in the endo form, and the maleic anhydride unit can lie closer to the cyclohexa 1,3-diene unit in the TS.

As the sigma bonds form (progress along reaction co-ordinate to products) the C11-C12 and C14-C16 are pushed closer to each other (typical C-C single bond length is 1.54 amstrongs) although the molecule will orientate ittself to minimise steric repulsions, the exo form will still experience significantly more strain than the endo form and hence the resultant product will be higher energy.

It has also been postulated that there is a favourable secondary orbital overlap between the pi systems in the endo form which leads to a shortening of the distance between them in the transition state nd a lowering of the transition state energy. The MO's of the transition states will be examined to investigate this.

Energies

In order to predict the major product of the reaction between maleic anhydride and cyclohexa 1,3-diene the energies of the transition states were retrieved from the log files. These were compared to the energies of the B3LYP/6-31G* optimised reactants and activation energies calculated.

The calculations for the optimised reactants can be found on D-space at:

Cyclohexa 1,3-diene:http://hdl.handle.net/10042/to-2067

Maleic Anhydride:http://hdl.handle.net/10042/to-2068

	Endo TS	Exo TS	cyclohexa1,3-diene	maleic anhydride
Electronic Energy in Hartrees	-612.68339677	-612.67931092	-233.41891049	-379.28954454
Activation energy in Hartrees	0.02505826	0.02914411
Activation energy in Kcal/mol	15.72428367434	18.28819132
Sum of electronic and zero-point energies at 0K in Hartrees	-612.502141	-612.498012	-233.296099	-379.233654
Activation energy in Hartrees	0.027612	0.031741
Activation energy in Kcal/mol	17.3267785	19.9177631
Sum of electronic and thermal energies at 298.15 K in Hartrees	-612.491787	-612.487662	-233.290923	-379.228470
Activation energy in Hartrees	0.027606	0.031731
Activation energy in Kcal/mol	17.3230134	19.9114880

The units were converted from Hartree to Kcal/mol using the relationship 1 hartree = 627.509 kcal/mol

The activation energies are calculated from the total energy of the reactants (i.e. summation of the energies of cyclohexa1,3-diene and malaic anhydride which are given in the table below.

Total Electronic Energy in Hartrees	-612.70845503
Total Sum of electronic and zero-point energies at 0K in Hartrees	-612.529753
Total Sum of electronic and thermal energies at 298.15 K in Hartrees	-612.519393

The endo and exo products were also draw in in gaussview and optimised to the DFT B3LYP 6/31-G* level in order to see which was the most thermodynamically favoured product.

The calculations can be found on D-space:

Endo product:http://hdl.handle.net/10042/to-2076

Exo product:http://hdl.handle.net/10042/to-2083

Product	Endo	Exo
Electronic Energy in Hartrees	-612.75828991	-612.75528528
Sum of electronic and zero-point energies at 0K	-612.572059	-612.569384
Sum of electronic and thermal energies at 298.15 K	-612.562591	-612.559981

The table above shows that the endo transition state is lower energy than the exo, and hence one can conclude that when the reaction is under kinetic control and when it is under thermodynamic control the endo isomer will be the favoured product. This is as it has both a lower activation energy (kinetically favoured pathway) and leads to a lower energy product (thermodynamically favoured).

Both activation energies are relatively low and hence the reaction would be predicted to require gentle heating only.

Visualising the MO's

It has been potulated that the endo selectivity observed in many diels alder reactions is caused by a lowering in the energy of the endo transition state by favourable secondary orbital overlaps.

In order to investigate the postulated secondary orbital overlaps in the endo transition states the MO's of the B3LYP/6-31G* optimised transition states were visualised. In order to gain a clearer picture of what orbitals these MO's are comprised of the MO's of the B3LYP/6-31G* optimised products were also visualised. However as the MO mixing is complex, this is hard to deduce but a reasonable idea can still be seen.

Molecule	Endo TS	Exo TS	cyclohexa1,3-diene	maleic anhydride
HOMO-1
Energy	-0.266	-0.263	-0.299	-0.326
Symmetry	Symmetric	Symmetric	Symmetric	Symmetric
HOMO
Energy	-0.242	-0.242	-0.205	-0.229
Symmetry	Antisymmetric	Antisymmetric	Antisymmetric	Asymmetric
LUMO
Energy	-0.067	-0.078	-0.017	-0.117
Symmetry	Antisymmetric	Antisymmetric	Asymmetric	Asymmetric

Secondary Orbital Overlap Effect

Secondary orbital interactions are defined as interactions occurring other than those used to define wether or not a reaction is allowed. The primary orbital interactions are the ones that form the formal bonds.

The endo selectivity of the diels alder reaction was proposed to be due to these kind of interactions by Woodward and Hoffmann in 1965, who proposed that the p-orbitals of the two pi systems formed a favourable overlap in the endo transition state, lowering it's energy. This overlap is not present in the exo transition state and so this is higher energy. Alder and Stein proposed a similar 'endo rule' which says that the endo transition state is favoured as it has the maximium accumulation of double bonds..

However the endo selectivity can be due to other factors. It has been proposed that steric hindrance in the exo transition state and increased van der waals attractive interactions in the endo transition state. Some other theories include ones based on differential volumes of activation and different polarities of the transition states. The endo transition state is also postulated to allow more favourable charge transfer between the reactants. The existance of secondary orbital overlap is still an unresolved matter. Computational chemistry can help to visualise MO's and reaction pathways and thus answer this question for individual systems modelled at least. Extensive calculations have been published in recent literature on this issue and it is still an area of current research.

Thus it is necesary to model the MO's of the individual system in order to gain an answer.

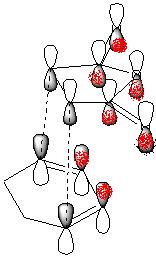
A diagram showing the primary (grey P-orbitals) and postulated secondary (red p-orbitals) interactions for the reaction I am modelling, according to the Woodward-Hoffman SOI theory for this reaction is shown below.

Examining the computed MO's of the two transition states above leads me to believe that no secondary orbital overlap is occurring in the HOMO.

This is as the side view of the HOMO of the endo isomer shows that the p-like lobe on the carbonyl oxygens is parallel to the pi system on the doubly bonded carbons below it. Thus any bonding type interaction is cancelled by an equal amount of antibonding. The two are of differenct symmetry and do not mix. No increase in the size of the lobes between the O=C-O-C=O fragment and the pi system below is seen, which would be expected if a secondary interaction was occuring. Electron density is not polarised towards the expected region and only the primary interaction can be seen.

This result can be rationalised by considering the fact that in both the reactants and the transition states there are no 'p atomic orbitals' as such, as these have mixed to form molecular orbitals. These MO's can of course mix with each other when of the correct symmetry and similar energy. If mixing did occur between an MO which resembled the pi orbital of the cyclohexa1,3-diene and one which resembled the conjugated system in the maleic anhydride it would lead to the MO's of the transition states being markedly different, which is not seen.

The HOMO of the exo isomer looks identical to that on the endo except with the maleic anhydride component flipped over. If a secondary interaction was occuring I would expect the MO's to be different shapes.

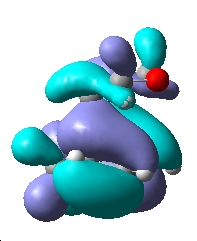
In the HOMO-1 there does appear to be an area between the maleic anhydride unit and the diene unit in which pi-like orbitals on the C=O are of the same phase and are pointing towards pi-like oprbitals on the diene. The orbitals have not mixed in the MO but a weak interaction may be present. In order to investigate this further calculations were carried out using a similar system in which the two carbonyl groups are replaces by CH2 groups, removing this interaction.

Further investigation

Introduction

In order to try to deduce if secondary orbital interactions are occurring and stabilising the endo transition state in the reaction of cyclohexa1,3diene and maleic anhydride, the transition states for the reaction shown below were computed. This system is similar but the carbonyl pi system thought to be responsible for the secondary overlap interactions has been removed and no carbon p-orbitals are present to overlap as the relevant carbons are now sp3 hybrised.

Computing transition states

Calculation of the transition states was done using the frozen co-ordinates method as for the previous reaction. The calculations were done first to the HF 3-21G level and then to the DFT 6/31G* level.

The products and reactants were also optimised up to this level in order to compute the activation energies.

D-space calculations All the calculations can be found on D-space.

Reactant:http://hdl.handle.net/10042/to-2079

Endo TS:http://hdl.handle.net/10042/to-2088

Exo TS:http://hdl.handle.net/10042/to-2089

These files were checked to ensure that a negative vibration corresponding to the diels alder reaction mechanism was present, which it was in bothe cases.

	Endo TS	Exo TS
Image of vibration
Frequency cm-1	-504	-503

Energies

If a secondary orbital overlap was significantly stabilising the endo transition state with respect to the exo in the cyclohexa1,3diene and maleic anhydride system, then I would expect that upon removal of this overlap the endo transition state would be destabilised with respect to the exo and hence the two would be closer in energy. Obviously upon making the carbons SP3 hybridised the steric interactions between the two reactants will increase and so both transition states are of a higher energy than those in the previous system. The activation energies were calculated as before.

Energy of cyclohexa1,3diene = -233.41891049

Energy of 2,5 dihydrofuran = -231.21587020

Total energy of reactants = -464.63478069

Comparison table

Endo	Exo	Difference
Electronic TS energy	-464.59322718	-464.59144986	0.00177732
Activation energy	0.04155351	0.04333083	0.00177732
Maleic Anhydride system TS Electronic energy	-612.68339677	-612.67931092	0.00408585
Maleic Anhydride system Activation energy	0.02505826	0.02914411	0.00408585

Energies all given in Hartree.

The data above show that the difference between the activation energies (i.e. energies of transition states) are in fact smaller in the 2,5 dihydrofuran reaction. This implies that there is a stabilising secondary orbital interaction in the maleic anhydride reaction lowering the energy of the endo transition state that does not occur in the case of the 2,5 dihydrofuran reaction. However it could be due to a number of other factors also so further investigation into the geometry and MO's in the system is needed.

Geometries

The geometries of the two transition states were examined and the results shown below. (Using the same numbering system as was used for the maleic anhydride reaction.)

	Endo	Exo
C6-C2 length in amstrongs	2.28	2.30
C11-C14 length in amstrongs	3.20	3.18
C14-C2-C6-C11 dihedral angle	57.8	50.9

As can be seen from the table above the forming C-C simgma bond distance is only very slightly longer in the exo transition state. The distance between the C11 and C14 however is slightly shorter. This is not in keeping with the idea that a secondary orbital interaction is occurring as the endo transition state would be expected to have a shorter distance in that case. The dihedral angle is significantly larger in the endo transition state which again is not in keeping with the proposed secondary orbital overlap. Thus the geometry also implies that this is not occurring and that the steric interactions dominate the structure and energy of the transition states.

MO's

The MO's were visualised in order to see how they differed for each case and to rationalise the difference in energy seen between the two transition states.

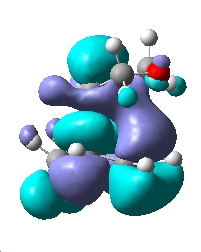
MO	HOMO-1	HOMO	LUMO
Endo TS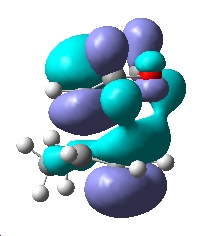
Symmetry	Symmetric	Antisymmetric	Symmetric
Exo TS
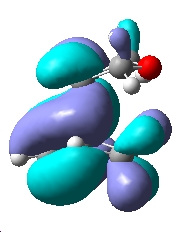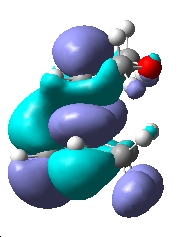
Symmetry	Symmetric	Antisymmetric	Symmetric

As can be seen above the HOMO of the transition states appear simialr to those in the previous system and do not show any significant secondary orbital overlap. The lumo-1 shows there is definate interaction of the diene pi system with the atoms situated vertically above it. This orbital is unoccupied though and so is unlikely to have a great effect. However the HOMO-1 shows a significant overlap of orbitals on the diene and those corresponding to the C-H sigma bond. The result is the MO has a region between these two groups of increased electron density. This is not present in the exo isomer, whose HOMO-1 is markedly different. Hence upon going from a conjugated to a non conjugated system it appears secondarty orbital interactions have increased! There is still antibonding interactions present in the region between the oxygen and the pi-cloud based orbital regions which may account for why a significant energy stabilisation and effect on geometry is not seen. As the orbitals discussed have in fact mixed to give the MO shown, it is not strictly a 'secondary orbital interaction' as the isolated orbitals do not exist. Rather it is a change in the shape of the MO's resulting in a region of bonding nature between the conjugated part of the diene and the two SP3 hybridised carbons on the 2,5 dihydrofuran. Hence the geometry and energy differences in the transition states imply that a secondary orbital overlap occurs in the maleic anhydride system but not (or much less so) the 2,5dihydrofuran system, the MO analysis seems to be implying the opposite.

Conclusions

From my investigations I have found that secondary orbital overlap, in terms of those proposed by Woodward-Hoffman fromtier molecular orbitals approach do not strictly exist. The AO's in molecules mix to form the MO's. Thus the expected overlaps are not seen. What is possible is mixing of the AO's to generate MO's in which the region reminiscant of the diene pi-bond clearly interacts with the atoms above it to form an MO with some bonding character in this region. The result is a shortening of the distance between these two fragments.

As the MO's have all mixed the presence or magnitude of this overlap cannot be predicted, nor can its effect. This is shown in the two reactions studied where one would expect a good overlap between the conjugated pi systems on the diene and maleic anhydride, and a smaller one in the 2,5-dihydrofuran which has no such pi system. Hence a computation of MO's must be run for each individual system of interest. However the energy difference and geometry of the maleic anhydride transition states imply they have the larger secondary orbital overlaps.

Even though there was some interaction between the CH2 and diene in the HOMO-1 of the endo transition state of the 2,5-dihydrofuran system, a significant increase in stability of the endo transition state relative to the exo was not seen compared to the maleic anhydride transition state. This implies that even when overlap between these groups occurs it is not the dominant factor stabilising the endo transition state.

My results lead me to believe that secondary orbital overlap is not a sound theory on which to base predictions or explinations of diels alsder selectivity. Although it provided a logical rationalisation of endo selectivity in the past, this approach has been surpassed by advances in technology allowing the MO's to be calculated and the explicit interactions viewed. This is a much better method and has found recent uses in designing diels alder reactions with desired endo or exo selectivities.

Notes on the calculations

The calculations I carried out were in the absence of other molecules and just considered the reactants, transition states and products as isolated molecules. In reality of course this reaction is done in a solvent and there are thus many surrounding solvent molecules. Othe reactant and product molecules will also be present in the solution. Many interactions between these molecules will obviously occur and this could give rise to a change in energy/geometry or favour a paticular reaction pathway over another. The kinetic energy of the reacting molecules has also been ignored and the calculations carried out just look at the energies on a static potential energy surface. Thus the good correlation of my calculations on the cope rearrangement with those observed experimentally is somewhat surprising given that these interactions have been ignored.