Rep:Mod:FirstAttempt
NH3 Molecule Properties
Bonding in NH3
(After Optimization)
Bond Length: 1.01798 Angstroms
Bond Angle: 105.74115 Degrees
Calculation Method: RB3LYP
Basis Set: 6-31G(D,P)
Final Energy: -56.55776862au
Point Group: 3Cv
File:NICHOLAS WOOD NH3 OPTIMISATION CALCULATION 2.LOG
Optimized NH3 Molecule |
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986271D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
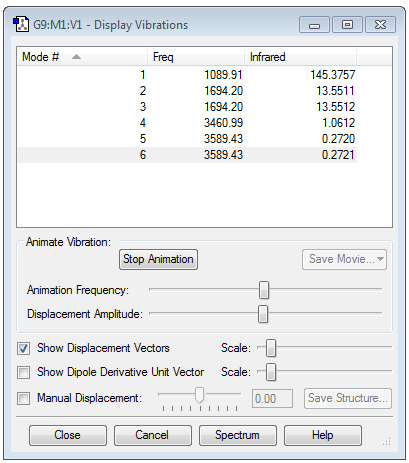
Vibrational Modes in NH3
6 Vibrational Nodes are seen due to the 3N-6 rule being (3x4)-6 as there are 4 atoms involved
Modes 2 and 3 and Modes 5 and 6 have the same energy as each other respectively and so are degenerate
Modes 1,2 and 3 are all 'Bending' while Modes 4,5 and 6 are all 'Bond Streching' and Mode 4 is highly symmetric
Mode 1 is known as the 'umbrella' mode due to the way the bonds bend in its vibrational state
As Modes 2 and 3 and Modes 5 and 6 have similar energies only 4 bands would be seen in the spectra of this molecule. However due to the low intensities of Modes 5 and 6, and even possibly Mode 4, it is possible that they may get caught up in the background noise of the spectrometer and not be seen either.
Charge Distribution in NH3
The charge distribution shows the expected results due to the electronegativity of the nitrogen atom. This means there is a higher distribution of electrons surrounding the nitrogen as it has drawn some of the electron density away from the hydrogens, producing the expected negative charge on the nitrogen. However as the hydrogens are less electronegative than the nitrogen, the values are positive as they are slightly electron deficient.
N2 Properties
(After Optimization)
Bond Length: 1.10550 Angstroms
Bond Angle: 180 Degrees
Calculation Method: RB3LYP
Basis Set: 6-31G(D,P)
Final Energy: -109.52412868au
Point Group: D*H
File:Nicholas Wood N2 OPTIMIZATION.LOG
Optimized N2 Molecule |
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400936D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
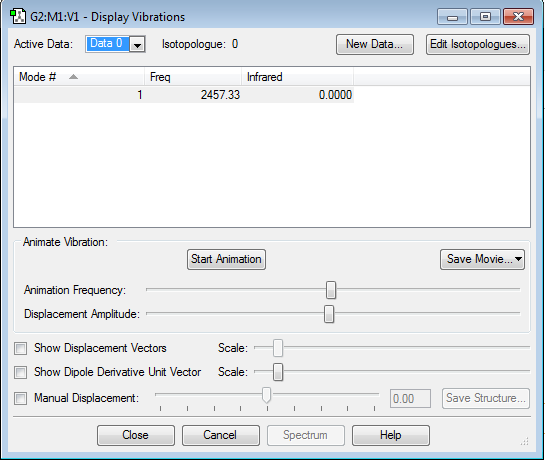
As shown by the table, only one vibrational state is observed as the molecule is linear.
H2 Properties
(After Optimization)
Bond Length: 0.74279 Angstroms
Bond Angle: 180 Degrees
Calculation Method: RB3LYP
Basis Set: 6-31G(D,P)
Final Energy: -1.17853936au
Point Group: D*H
File:Nicholas Wood H2 OPTIMIZATION.LOG
Optimized H2 Molecule |
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164079D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
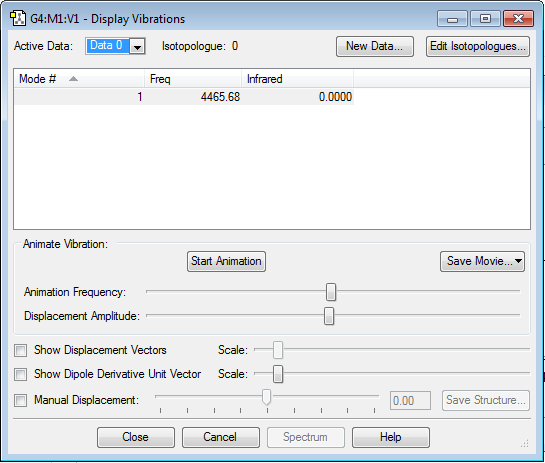
As shown by the table, only one vibrational state is observed as the molecule is linear, but with a higher frequency than N2
Reaction Energy of Haber-Bosch Process
E(NH3)= -56.55776862au
2*E(NH3)= -113.11553736au
E(N2)= -109.52412868au
E(H2)= -1.17853936au
3*E(H2)= -3.53561808au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= (-113.11553736) - (-109.52412868-3.53561808) = -0.0557906au
ΔE in kJ/mol = -146.4782203
Due to the ΔE of the Haber process being negative, this shows that the reaction is thermodynamically favourable as the reaction gives out energy as it is formed, showing that the ammonia product is more thermodynamically stable.
H2O Properties and Molecular Orbitals
(After Optimization)
Bond Length: 0.96522 Angstroms
Bond Angle: 103.745 Degrees
Calculation Method: RB3LYP
Basis Set: 6-31G(D,P)
Final Energy: -76.41973740au
Point Group: C2v
File:Nicholas Wood H2O OPTIMIZATIOB 3.LOG
Optimized H2O Molecule |
Item Value Threshold Converged?
Maximum Force 0.000099 0.000450 YES
RMS Force 0.000081 0.000300 YES
Maximum Displacement 0.000128 0.001800 YES
RMS Displacement 0.000120 0.001200 YES
Predicted change in Energy=-1.939669D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.9652 -DE/DX = 0.0001 !
! R2 R(1,3) 0.9652 -DE/DX = 0.0001 !
! A1 A(2,1,3) 103.7454 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
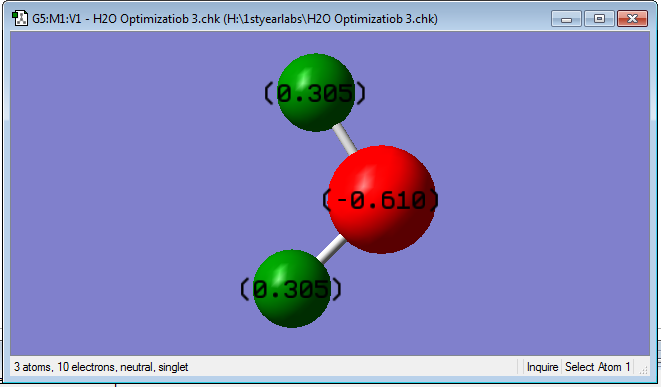
Due to the electronegativity of the oxygen, electron density is drawn towards it, shown by the negative charge on the atom, while the hydrogens are therefore electron deficient so have a slightly positive charge. The charge distribution is equal across both hydrogens due to it's linear structure so both hydrogens have the same charge value.
The occupied molecular orbitals in H2O
The 1st MO is the 1s AO for the oxygen atom which has a very low energy value of -19.13799 and so there is no mixing of it with any other AOs from the hydrogen. The next highest MO is a mix of the 2s AO on the oxygen and the 1s on the Hydrogens and is the bonding orbital, which is lower in the energy than the anti-bonding orbital between these AOs. The anti-bonding orbital is actually the 4th highest in energy, with the MO from the interaction between the 2px in the Oxygen and 1s in the Hydrogens contributing to it's value. The third highest occupied MO is from the 2px in the Oxygen and the 1s in the Hydrogens. The highest occupied MO (HOMO) is the 2pz AO with a pair of electrons in which have not interacted with the AOs from the Hydrogen. MO 6 is the LUMO in the H2O molecule, which has a value just over 0.