Rep:Mod:Fionnswiki
NH3 Molecule
Summary
| Calculation method | RB3LYP |
| Basis Set | 6-31G(D.P) |
| Energy | -56.55782 |
| RMS Gradient | 0.00000485 |
| Point Group | C3v |
| N-H bond length | 1.01798 Å |
| H-N-H bond angle | 105.741° |
Item Table
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986261D-10 Optimization completed. -- Stationary point found.
3D Jmol
test molecule |
The optimisation file is linked here
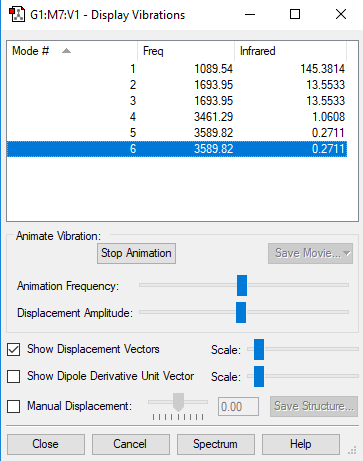
Frequency Analysis
| Frequency | Infrared |
|---|---|
| 1090 | 145 |
| 1694 | 14 |
| 1694 | 14 |
| 3461 | 1 |
| 3590 | 0 |
| 3590 | 0 |
From the 3N-6 rule, you would expect 6 vibrational modes (3x4-6=6).
Modes 2 & 3 and 5 & 6 are degenerate
Modes 1 , 2 & 3 are bending vibrations Modes 4 , 5 & 6 are bond stretch vibrations
Mode 4 is highly symmetric Mode 1 is the umbrella mode
You would expect to see 2 bands in an experimental spectrum of gaseous ammonia
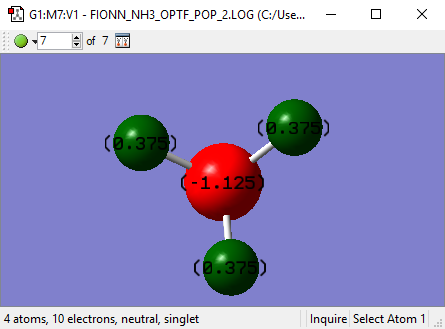
Charge Analysis
The Charge on the nitrogen is -1.125 and the charge on the hydrogen is +0.375 which is as you would expect due to the electronegativity of nitrogen.
N2
Summary
| Calculation method | RB3LYP |
| Basis Set | 6-31G(D.P) |
| Energy | -109.52413 au |
| RMS Gradient | 0.00000060 au |
| Point Group | Dinf h |
| N-N bond length | 1.10550 Å |
Item Table
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000002 0.001800 YES
RMS Displacement 0.000003 0.001200 YES
Predicted change in Energy=-1.248808D-11
Optimization completed.
-- Stationary point found.
3D Jmol
test molecule |
The optimisation file is linked here
Frequency Analysis
| Frequency | Infrared |
|---|---|
| 2457 | 0 |
As you can see, there is only one vibrational mode. We can find this out, because we know that N2 is a linear molecule, so we use the 3N - 5 rule which gives us an answer of 1 vibrational mode.
H2 Molecule
Summary
| Calculation method | RB3LYP |
| Basis Set | 6-31G(D.P) |
| Energy | -1.17854 au |
| RMS Gradient | 0.00013423 au |
| Point Group | Dinf h |
| H-H bond length | 0.74247 Å |
Item Table
Item Value Threshold Converged?
Maximum Force 0.000232 0.000450 YES
RMS Force 0.000232 0.000300 YES
Maximum Displacement 0.000305 0.001800 YES
RMS Displacement 0.000431 0.001200 YES
Predicted change in Energy=-7.091616D-08
Optimization completed.
-- Stationary point found.
3D Jmol
test molecule |
The optimisation file is linked here
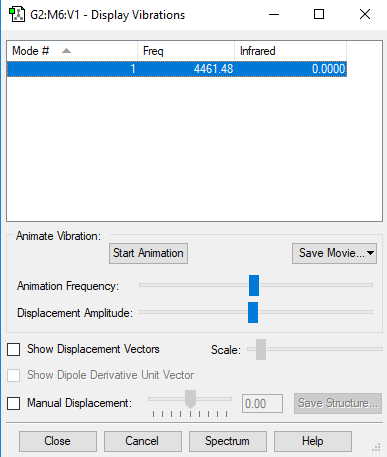
Frequency Analysis
| Frequency | Infrared |
|---|---|
| 4461 | 0 |
As you can see, there is only one vibrational mode. We can find this out, because we know that H2 is a linear molecule, so we use the 3N - 5 rule which gives us an answer of 1 vibrational mode.
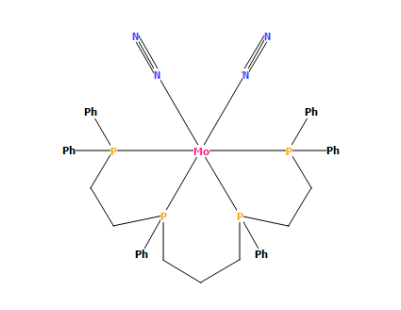
Bis(dinitrogen)-(1,1,4,8,11,11-hexaphenyl-1,4,8,11-tetraphosphaundecane)-molybdenum ([AQUVOY])
([AQUVOY])==
The N2 bond lengths in the molecule are 1.111 & 1.121 Å
However the N2 bond length when it isn't a ligand is 1.106 Å
The bond length of N2 is longer when it's a ligand than when it is on its own. This is because the central transition metal in the complex is electron withdrawing, which weakens the N-N bond and hence it is slightly longer. Also, the transition metal complex is in solid phase, and the N2 molecule is in gaseous phase. In solid phase, there are lots of molecules closely packed together that all interact and so electron density is spread even more, further weakening the N-N bond. In gaseous phase, the molecules are spread out so the intermolecular interactions have less effect.
The Energy Changes of the Harber-Bosch Process
N2 + 3H2 => 2NH3
| Molecule | Energy (au) | Number of Moles in reaction | Number of Moles x Energy |
|---|---|---|---|
| N2 | -109.52413 | 1 | -109.52413 |
| H2 | -1.17854 | 3 | -3.53562 |
| NH3 | -56.55782 | 2 | -113.11564 |
ΔE for this reaction is equal to the sum of the product energies - the sum of the reactant energies:
ΔE calculation
=2xE(NH3)-[E(N2)+3xE(H2)]
= [-113.11564]-[-109.52413 -3.53562]
= -0.05589 au
= -146.74 kJ/mol
From this information we can conclude that the gaseous products ammonia is more stable as the overall energy decreases during the reaction (exothermic).
Cl2
Summary
| Calculation method | RB3LYP |
| Basis Set | 6-31G(D.P) |
| Energy | -920.34988 au |
| RMS Gradient | 0.00002511 au |
| Point Group | Dinf h |
| Cl-Cl bond length | 2.04174 Å |
Item Table
Item Value Threshold Converged?
Maximum Force 0.000043 0.000450 YES
RMS Force 0.000043 0.000300 YES
Maximum Displacement 0.000121 0.001800 YES
RMS Displacement 0.000172 0.001200 YES
Predicted change in Energy=-5.277268D-09
Optimization completed.
-- Stationary point found.
3D Jmol
test molecule |
The optimisation file is linked here
Frequency Analysis
| Frequency | Infrared |
|---|---|
| 520 | 0 |
As you can see, there is only one vibrational mode. We can find this out, because we know that Cl2 is a linear molecule, so we use the 3N - 5 rule which gives us an answer of 1 vibrational mode.
Charge Analysis
The charge on both chlorine atoms is 0, which we would expect because they have the same electronegativity.
Molecular orbitals
3σg
Energy= -0.933 au
This is the bonding molecular orbital form fromed the combination of the 3s orbitals on the Cl atoms. It contains 2 electrons.
3σ*u
Energy= -0.777 au
This is the antibonding molecular orbital formed from the combination of the 3s orbitals on the Cl atoms.
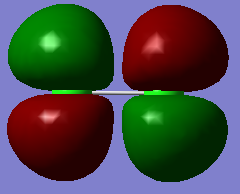
4σg
Energy= -0.474 au
This is the bonding molecular orbital formed from the combination of one of the 3p orbitals from each Cl atom, the one that runs along the bond which we will call 3pz. Because the 4σ*u orbital is empty, and this orbital contains 2 electrons, there is a σ bond between the two Cl atoms.
2πu
Energy= -0.407 au
There are 2 degenerate 2πu orbitals, one formed from the combination of the two 3px AOs and one formed from the two 3py AOs. Both orbitals are filled with 2 electrons. The p orbitals are in phase with each other and therefore this is a bonding MO.
2π*g
Energy= -0.314 au
Similarly to the 2πu orbitals, the 2π*g orbitals are formed from the combination of two 3px AOs or two 3py AOs, however the two AOs are out of phase this time which means the 2π*g orbital is an antibonding orbital. Both of these orbitals are filled too and so there is no π bonding in the system. This orbitals is also the highest energy filled orbital, so is called the HOMO.
4σ*u
Energy= -0.142 au
This orbital is not filled, and is the lowest energy unfilled orbital so is called the LUMO. It is formed from the out of phase combination of two 3pz orbitals.
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have recieved your grade from blackboard.
Wiki structure and presentation 0.5/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
However you have left the caption for each of your jmol files as "test molecule" which is unhelpful for the reader.
NH3 0.5/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
No
Have you included answers to the questions about vibrations and charges in the lab script?
You have answered the vibrational questions correctly, well done.
However an explanation of why you only see two peaks in the spectrum is missing.
Your explanation of the charges is also incomplete - you need to compare the electronegativity of N to that of H to explain the electron distribution.
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES - well done!
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 5/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES - very good explanations for both.
Independence 0/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or Do some deeper analysis on your results so far
No independent work included.