Rep:Mod:FR0261

Introduction

In this computational experiment, the transition structures of the Cope Rearrangement and several Diels-Alder reactions will be characterised on potential energy surfaces using GaussView. The geometries and energies of these structures will be computed at two levels of theory: HF/3-21G and B3LYP-3-61G*. 3-21G is a simple basis set, while B-31G* improves on it by adding polarization to all atoms and improving the modelling of core electrons. The geometries and energies of the structures will be compared to previous studies using similar computational methods and to experimental data.

The Cope Rearrangement

Introduction

Cope rearrangement

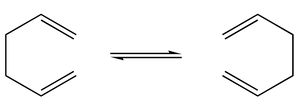
The Cope rearrangement of 1,5-hexadiene is [3,3]-sigmatropic reaction proceeding via either a chair or a boat transition structure. The energies and geometries of both transition structures as well as the reactant and product will be studied computationally to determine the preferred reaction mechanism.

Optimisation of Reactants and Products

Before studying the transition structures, the geometries and energies of the reactant and product molecules must be calculated. Multiple conformations of 1,5-hexadiene exist with similar energies . The molecule has 3 C-C single bonds which can rotate, each of which has 3 rotational minima, giving rise to 27 conformations. Only 10 of these are energetically distinct, these are shown in Appendix 1.

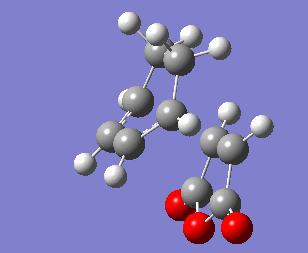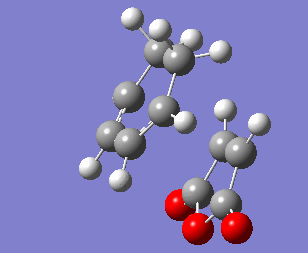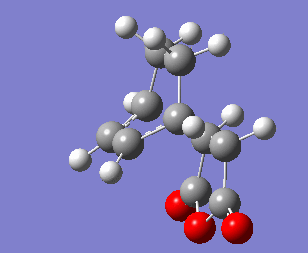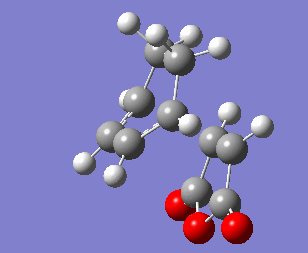
A molecule of 1,5-hexadiene (conformer 1) was drawn in GaussView with an anti linkage between the central four carbon atoms (a dihedral angle of 180°) and the structure was cleaned. It was then optimised to a minimum using the Hartree-Fock method with a 3-21G basis set, henceforth referred to as the HF/3-21G level of theory, generating chk and log files of the optimised structure. Its geometry and energy match the anti1 conformer.

A second molecule of 1,5-hexadiene (conformer 2) was drawn with a gauche linkage (dihedral angle: -60°) then cleaned. This structure is expected to have a higher energy than its anti-linkage counterpart due to steric repulsions between hydrogens on terminal carbon atoms. This was confirmed by the calculation, although the difference in energies is small.

The lowest energy conformation of 1,5-hexadiene is predicted to have a gauche(120°)/anti/gauche(120°) conformation. This structure was drawn, cleaned and optimised as above. The structure generated corresponds to the anti1 conformer.

The anti2 conformer (conformer 3) was drawn with gauche(-120°)/anti/gauche(120°) dihedral angles. It was cleaned, locked to Ci symmetry and optimised to a minimum. The energy obtained matched the energy given in the table.

Conformer	Structure	Point Group	Energy/Hartrees HF/3-21G
1		C1	-231.69260
2		C1/C2	-231.691667
4		Ci	-231.692535

This structure was re-optimised at a higher level (B3LYP/6-31G*) using the DFT method and the 3-61G basis set. The final energy was close to, but slightly higher than the result in the table at -234.55971588 a.u.

Optimised Reactant (anti2).

A frequency calculation was run on the re-optimised structure at the B3LYP/3-61G* level. The calculation was repeated at T = 0.1 K in order to see results close to those at T = 0 K (Gaussian would not run that calculation).

	Sum of Electronic and Zero Point Energies	Sum of Electronic and Thermal Energies	Sum of Electronic and Thermal Enthalpies	Sum of Electronic and Thermal Free Energies
298.15K	-234.416222	-234.408946	-234.408002	-234.408002
0K	-234.416222	-234.416221	-234.416220	- 234.416221

Optimising the Chair and Boat Transition Structures

1,5-hexadiene can undergo Cope rearrangement via either a chair or a boat transition state. Both transition states will be drawn and optimised at two levels of theory and their energies compared to determine the preferred reaction path. The intrinsic reaction coordinate from each transition state will be calculated to determine the conformation of 1,5-hexadiene generated by the rearrangement.

Chair Transition State	Boat Transition State

The Chair Transition State

A CH₂CHCH₂ fragment was drawn and optimised at the HF/3-21G level. It was duplicated then oriented so the two allyl fragments were arranged in the chair transition state. The distances between terminal carbons from each fragment were set to 2.20Å. The structure was copied so two different optimisation methods could be tested:

• Optimisation to Berny Transition State

The structure was optimised to a transition state (Berny) and a frequency calculation carried out.

The frequency calculation gave one imaginary frequency of magnitude 817.94 cm^-1, giving rise to the vibration below.The bond forming/breaking distances after optimisation were 2.02017 Å and 2.02010 Å.

• Optimisation using the Frozen Coordinate Method

The bond coordinates were frozen at 2.20A using the redundant coordinate editor. Optimisation was carried out as above, generating a structure that resembled the structure from the previous structure.

The bond forming/breaking distances were unfrozen in order to optimise them too. The distances were shortened to 2.02070 Å and 2.02075 Å.

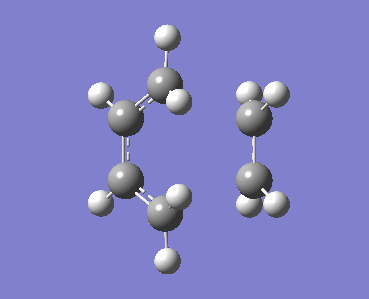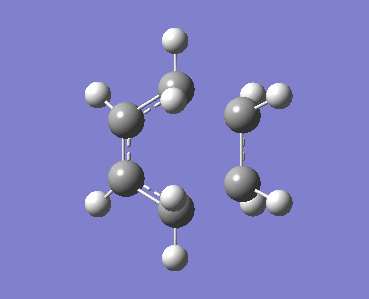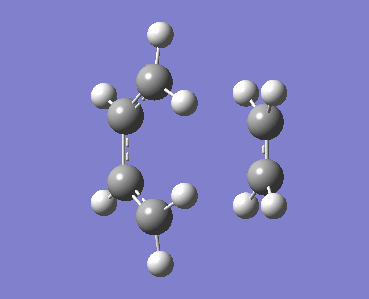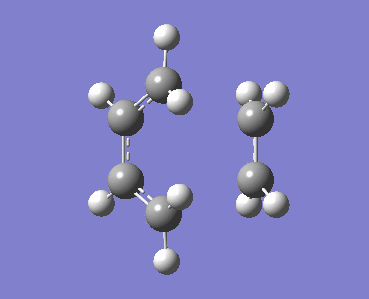
Optimised Chair Transition Structure.

The Boat Transition State

The optimised Ci reactant molecule created earlier was copied and pasted into two windows in GaussView, the first window corresponding to the reactant molecule and the second to the product. The atoms of the product molecules were renumbered to match the reactant molecule.

The structure was optimised to a transition state (QST2) and a frequency calculation run. The calculation fails and the structure generated is a dissociated chair with bonds beginning to form diagonally between the two fragments.

The original gjf file was reopened so that the reactant and product geometries could be modified before running the calculation. The central C-C-C-C dihedral angle was changed from 180° to 0° and both inside C-C-C angles set to 100° on both the reactant and product molecules so that they more closely resembled the boat transition structure. The QST2 calculation was run again, now generating a C2V boat transition state structure with one imaginary vibration of magnitude 840.00 cm^-1.

The boat transition state generated using the QST2 method was then used added as a third molecule group to the file with reactant and product structures. After inputting the geometry of a guess transition state, the QST3 method can be used to give a more reliable transition state structure. A C2V boat transition structure is generated again, with one imaginary vibration of magnitude 839.93 cm^-1. The difference in bond lengths and angles between the structures generated with the QST2 and QST3 methods is negligible.

Optimised Boat Transition Structure.

Chair Transition State	Boat Transition State

Intrinsic Reaction Coordinate

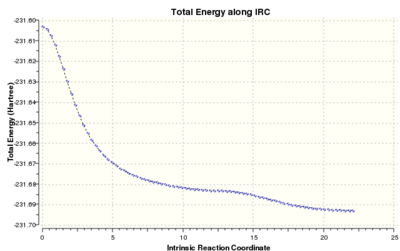
The optimised boat structure generated previously with the QST2 method was reopened to determine the intrinsic reaction coordinate (IRC) of the reaction passing through the boat transition state. The IRC was computed only in the forward direction since the reaction is symmetrical, calculating the force constants at each of the 50 steps at the HF/3-21G level of theory. 51 intermediate geometries were generated, the last of which had still not reached the minimum (product) geometry. This was confirmed by reading the log file, which stated "Maximum number of steps reached. Calculation of FORWARD path complete. Reaction path calculation complete."

The structure from the last point on the IRC was optimised to a minimum at the HF/3-21G level. This method optimised the structure to a local minimum where the two fragments were seperate rather than the product molecule, so a different approach was required.

Product from Boat Transition State

The IRC was recalculated as above, with the number of steps increased to 100. Only 77 steps were calculated because the PES minimum had been reached. As predicted, the minimum geometry was a molecule of 1,5-hexadiene. The central C-C-C-C bond angle was -67°, indicating that the boat transition structure connects gauche geometries. Its energy and geometry most closely resemble the gauche3 conformer from Appendix 1. The conformer has the lowest energy of all the 1,5-hexadiene conformers studied.

The IRC from the chair transition state was calculated starting with the structure generated initially by Berny optimisation to the transition state. The PES minimum was detected after 44 steps. The product structure is closest in appearance to the gauche3 conformation.

IRC from Boat TS	IRC from Chair TS

IRC path - Boat TS	IRC path - Chair TS

Transition Structure Activation Energies

The chair and boat transition structures optimised at the HF/3-21G level were reoptimised at the B3LYP/6-31G* level. Frequency calculations were then carried out at the same level on the reoptimised structures. At both levels of theory, the activation energy for the chair transition state is lower, indicating that this is the preferred reaction pathway.

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466698	-231.461340	-234.505467	-234.362681	-234.356766
Boat TS	-231.602802	-231.450928	-231.445298	-234.492914	-234.351364	-234.408572
Reactant (gauche3)	-231.692661	-231.539486	-231.532647	-234.559337	-234.415745	-234.408572

*1 hartree = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.68	44.75	33.30	32.51	33.5 ± 0.5
ΔE (Boat)	55.57	54.81	40.40	39.85	44.7 ± 2.0

At the HF/3-21G level of theory, neither reaction pathway had an activation energy in agreement with experimental data. The activation energies calculated using the higher B3LYP-3-61G* level were closer to experimental data and in the case of the chair transition state, in very good agreement.

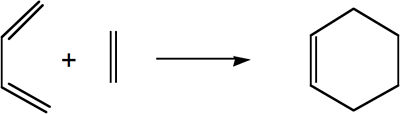
The Diels Alder Cycloaddition

The Diels-Alder reaction is a cycloaddition of two conjugated π systems, one contributing 4π elections and the other 2π elections. It is a 4n + 2 thermally allowed reaction and therefore proceeds via Hückel topology and has only suprafacial components.

The simplest Diels-Alder reaction is that of cis-butadiene (diene) with ethylene (dienophile), a [π4s + π2s] cycloaddition. The reaction occurs in a concerted stereospecific manner if the HOMO of one reactant can interact with the LUMO of the other so there must be significant overlap between the two molecular orbitals.

Ethylene+Butadiene cycloaddition

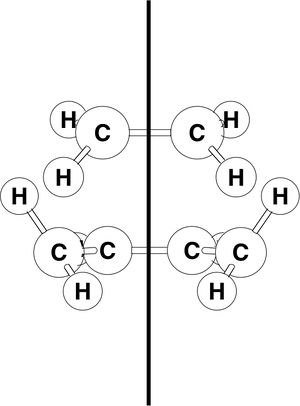
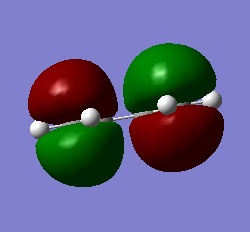
A molecule of cis-butadiene was drawn in GaussView and otpimised at the B3LYP/3-61G* level of theory using Gaussian. The HOMO and LUMO of the optimised structure were visualised. The LUMO is symmetric with respect to the reflection plane, while the HOMO is anti-symmetric. The HOMO of ethylene is symmetric and the LUMO anti-symmetric with respect to the plane shown to the right.

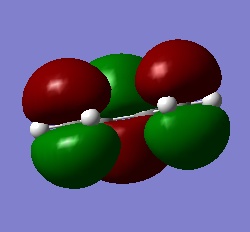HOMO of cis-butadiene (a)	LUMO of cis-butadiene (s)

Computation of the Transition State Geometry

A guess transition structure was drawn by first creating a bicylic system, deleting the CH₂-CH₂ fragment, then setting the two σ bonds formed in the reaction to partial bonds with the fragments 2.21Å apart. The structure was optimised to a transition state (Berny) at the HF/3-21G level. The geometry of the guess transition state was chosen to match previous computational studies at the same level of theory.

A frequency calculation was run at the same level of theory. The optimised structure had one imaginary frequency of magnitude 818.41cm^-1, confirming that it is a transition state. It had Cs/C1 symmetry. The structure was further optimised at the B3LYP-3-61G* level. The geometrical parameters of both optimised structures were compared to previous studies using the same basis sets and found to match well.

Diels-Alder Transition State

Bond Lengths in Å

	HF/3-21G				B3LYP/6-31G*
	C1-C2	C2-C3/C1-C6	C3-C4/C5-C6	C4-C5	C1-C2	C2-C3/C1-C6	C3-C4/C5-C6	C4-C5
Calculated TS	1.376	2.210	1.370	1.394	1.393	2.264	1.389	1.408
Reference TS	1.376	2.210	1.370	1.395	1.383	2.202	1.377	1.393

The distance between the carbons forming σ bonds was in both cases longer than the sp³ C-C bond length of 1.54 Å but shorter than the sum of carbon's Van der Waals radius (1.7 + 1.7 = 3.4 Å). There is a bonding interaction between the two carbon atoms in the transition state, but it is not as strong as a single bond. Where π bonds are being broken or formed, the bond length is only slightly greater than in an alkene (1.34 Å), indicating a high degree of π character to the bonds involved in the mechanism.

Numbering Scheme	Bond Lengths in TS

The vibration with an imaginary frequency corresponds to the reaction path at the transition state. The formation of the two bonds is synchronous based on this vibration, since it is symmetric with respect to the plane. The lowest positive frequency is asymmetric with respect to the plane: as two of the atoms forming a σ bond approach each other, the other two are separated. This would lead to stepwise formation of the two σ bonds.

Vibration of Imaginary Frequency	Vibration of First Positive Frequency

The HOMO and LUMO of the transition structure were both visualised and were both symmetric with respect to the plane. These MOs have been formed from the HOMO of cis-butadiene donating into the LUMO of ethylene, which are both antisymmetric and have significant overlap density. As a result the two MOs can interact so the reaction is allowed and will proceed via a concerted stereospecific mechanism.

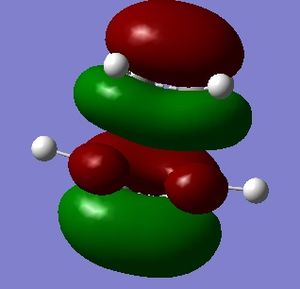HOMO of transition state (s)	LUMO of transition state (s)

Regioselectivity of the Diels-Alder Reaction

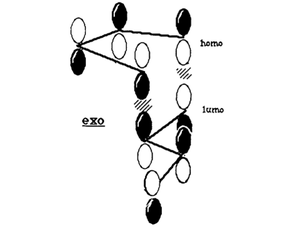
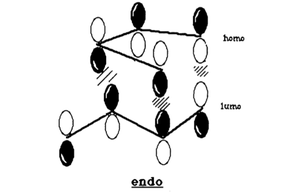
Unlike the example above, the Diels-Alder reaction of cyclohexa-1,3-diene with maleic anhydride can give rise to two distinct products via two different transition states: the exo and endo forms. The product will take the exo form if both new σ bonds are formed on the top face of the ring, or the endo for if the bonds are formed on the bottom face. The two transition structures will be optimised and compared.

The transition strucutre for the exo product was drawn in GaussView then optimised to a Berny transition state at the HF/3-21G level of theory using the redundant coordinate method. The optimised structure was reoptimised at the B3LYP/3-61G* level of theory. The presence of one imaginary frequency giving rise to the vibrations shown below confirms that these structures are transition states.

Exo Transition State

The same method was applied to a guess endo structure, but optimisation led to an exo structure. As well as freezing the length of the σ bond being formed, the angle between the maleic anhydride and the cyclohexadiene ring was frozen while the structure was optimised to a minimum, this time giving the endo structure. The bonds were unfrozen and the structure optimised to a Berny transition state at the HF/3-21G level of theory, then again at the B3LYP-6-31G* level.

Endo Transition State

Frequency calculations confirm that this is a transition structure, with the vibration of the imaginary frequency shown below.

Exo Transition State	Endo Transition State

Summary of energies (in hartree)

	B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Relative energies
Exo TS	-609.311169	-609.127792	-609.119248	3.18
Endo TS	-612.495478	-612.313973	-612.303642	0.0

Bond Lengths in Å

	B3LYP/6-31G*
	C1-C2	C2-C3/C1-C6	C3-C4/C5-C6	C4-C5
Endo TS	1.403	2.267	1.398	1.404
Exo TS	1.373	2.261	1.370	1.398

Bond Lengths in Transition Structures

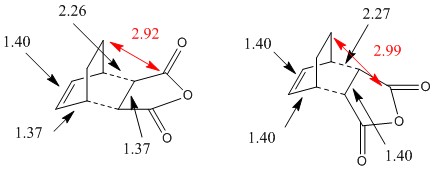
As with the previous Diels-Alder reaction, the bond lengths where π bonds are being formed and broken are slightly longer than C=C bonds but shorter than C-C, indicating π character to the bonds in the transition state.

The exo structure is higher in energy than the endo structure. It is strained by proximity of the -(C=O)-O-(C=O)- fragment to the -CH₂ group (2.92Å, smaller than twice the Van der Waals radius of carbon of 3.40Å). In the endo structure, the carbons of the -(C=O)-O-(C=O)- fragment are separated from those of the -CH=CH- fragment by 2.99Å so the structure suffers from less steric repulsion.

Secondary orbital overlap is the positive overlap of non-reacting orbitals in the frontier molecular orbitals of a pericylic reaction. In the endo transition state, there are strong secondary orbital interactions lowering the overall energy. These interactions are absent in the exo transition state. The frontier orbital interactions of the diene HOMO with the dienophile LUMO are shown below.

These orbital interactions can also be seen in the calculated HOMOs and LUMOs of the transition states, all antisymmetric with respect to the plane.

HOMO of Exo TS

HOMO of Endo TS

LUMO of Exo TS

LUMO of Endo TS

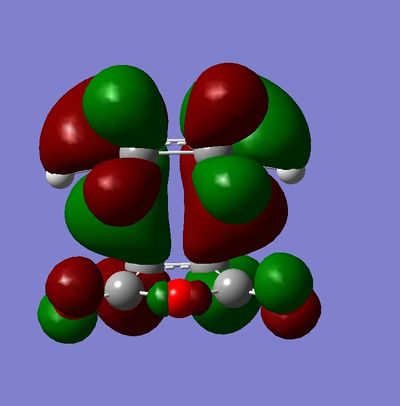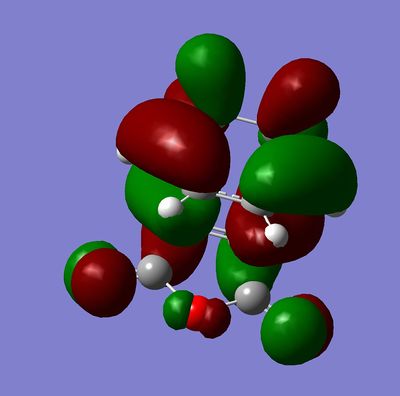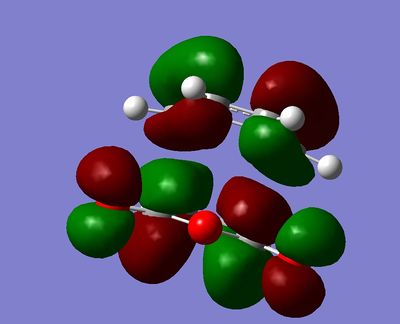This regioselectivity for the endo product is confirmed both by other computational studies and experimentally for this and many other Diels-Alder reactions.