Rep:Mod:FITF92

Part One: Conformational analysis using Molecular Mechanics

The Hydrogenation of Cyclopentadiene Dimer

Two equivalents of 1,3-cyclopentadiene (CPD) dimerises at room temperature to form dicyclopentadiene (DCPD) via a Diels-Alder reaction. One molecule of CPD behaves as the diene, whilst the other as the dienophile. The reaction results in two stereoisomers because the two molecules of CPD can approach each other in two distinct orientations.

Figure 1: Formation paths of exo- and endo- DCPD.

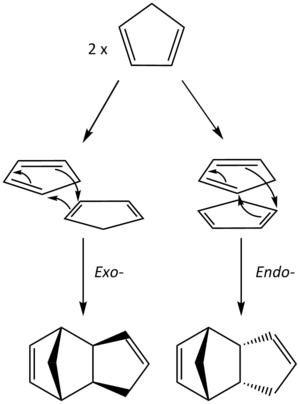
The exo- stereoisomer is formed when the substituent (non-reacting double bond) on the dienophile is directed away from the diene whereas the endo- isomer is formed when the substituent is directed towards the diene (Figure 1).

The reaction favours endo-DCPD formation over exo-DCPD (the endo rule). Using 3D modelling programs, Avagrado and ChemBio3D, it was possible using molecular mechanic calculations to determine why this is and whether the reaction is kinetically or thermodynamically controlled.

• 
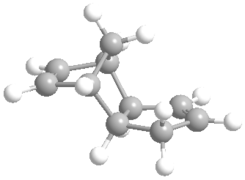
  Ball and stick model of Exo-DCPD.
• 
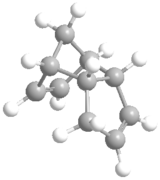
  Ball and stick model of Endo-DCPD.

The geometries of both isomers were optimised using Avagrado (Force Field=MMFF94s and Algorithm=Conjugate gradients). The following data was tabulated:

Table 1: Relative energies of Exo- and Endo- dimers.

Property	Exo- (kcal/mol)	Endo- (kcal/mol)
Stretch	3.54	3.46
Bend	30.78	33.22
Stretch-bend	-2.04	-2.08
Torsion	-2.73	-2.95
Van der Waals	12.79	12.33
Electrostatic interactions	13.01	14.18
Total energy	55.37	58.19

Figure 2: Mechanism of endo-DCPD formation showing the transition state.

Figure 3: Frontier orbitals of endo-DCPD.

From Table 1, it is clear that the more thermodynamically stable diastereoisomer is the exo-DCPD because its total energy is lower by 2.82 kcal/mol. This lower energy results from the exo- dimer having lower torsional strain (resistance to bond rotation between atoms that are vicinal) and lower angle bending energy (angle bending between geminal atoms). These relative energy terms represent deviations from "natural" values for the specific function, so the torsional and bending term are deviations from optimal dihedral and bond angles respectively. The bond between the norbornene and cyclopentene rings of the endo-dimer has a greater torsional strain because the two rings are in an eclipsed formation (or are facing each other). As a result, there is more van der Waals repulsion between the two rings which increases the potential energy of the molecule.

The reaction is kinetically controlled because the kinetic product (endo-) is formed more favourably over the more stable thermodynamic product (exo-). This suggests that the transition state of endo-DCPC must be lower (lower activation energy, greater rate constant) therefore it forms more quickly than exo-DCPD.

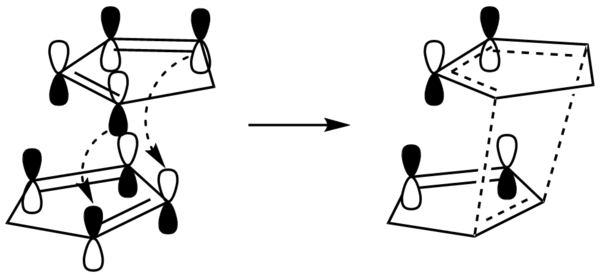
By studying the frontier orbitals (HUMO and LUMO orbitals) of endo-DCPD (Figure 3) it is apparent the back orbitals of the diene have the correct symmetry for favourable interactions with the back orbitals of the dieneophile. Although no bonds form between these orbitals, this favourable through space interaction stabilises the transition state and therefore lowers its energy hence endo-DCPD is the kinetic product.

A single step hydrogenation of DCPD breaks a single double bond, however since there are two distinct double bonds, the reaction is regioselective. The hydrogenation can either take place in the cyclopentene ring to yield dimer A or in the norbornene ring to yield dimer B. (Figure 4.)

Figure 4: Hydrogenation pathways of endo-DCPD.

Again, using molecular mechanical calculations, the relative ease of hydrogenation at each specific double bond can be obtained. The following data was tabulated:

Table 2: Relative energies of Dimer A and B.

Property	Dimer A (kcal/mol)	Dimer B (kcal/mol)
Stretch	3.31	2.82
Bend	30.85	24.68
Stretch-bend	-1.93	-1.66
Torsion	0.07	-0.38
Van der Waals	13.28	10.64
Electrostatic interactions	5.12	5.15
Total energy	50.72	41.26

Studying Table 2, dimer B is lower in total energy compared to dimer A by 9.46 kcal/mol thus dimer B is more thermodynamically stable. This difference in total energy mainly arises from the bending term (as discussed previously this is the deviation from optimal bond angle).

• 
  Figure 5: Dimer A showing bond angle of alkene in the norbornene ring.
• 
  Figure 6: Dimer B showing bond angle of alkene in the cyclopentene ring.

The optimal bond angle for an alkene is 120° but as shown clearly by Figure 5 and 6, both the bond angles for the alkene in dimer A and B are not at optimal, thus producing strain on the double bond. However, the bond angle for the double bond in dimer B is closer to optimal than in dimer A therefore is less strained. As a result, the double bond (being more strained) in the norbornene ring is more likely to break during hydrogenation to form dimer B.

Atropisomerism in an Intermediate related to the Synthesis of Taxol

Paclitaxel or its trademark name Taxol is a drug used in cancer chemotherapy. Figure 7 shows an important intermediate, compound C, in the synthesis of Taxol. Compound C, carbonyl group pointing up, can isomerise to an atropisomer where the carbonyl group in the molecule is pointing down, compound D. Furthermore, the alkene functional group in both compounds C and D show uncharacteristic slowed reactivity.

Figure 7: Intermediates C and D.

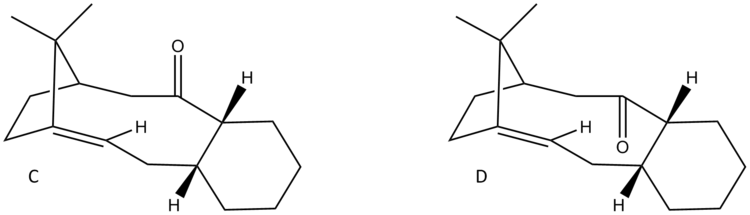
Atropoisomers are stereoisomers that arise due to restricted rotation about single bonds; the steric strain barrier to rotation is too high resulting in separate isomers. It was found (using 3D modelling and geometry optimisation) that both compounds C and D each have a possible of four different conformers; two chairs and two twist boats. Twist boat conformations are higher in energy and therefore are less stable than chair conformations due to greater angle and torsional strain. The more thermodynamically stable conformation (lowest total energy) is the major product and to find this, molecular mechanic calculations were performed on the chair conformations of both C and D. (The energies of the twist boat conformations of both C and D were not regarded as their energies are already too high.)

The following data was collected after optimising the geometries (using MMFF94s force field) of the species C and D.

Table 3: Relative total energies of the chair conformers of C and D.

Property	C conformer 1	C conformer 2	D conformer 1	D conformer 2
Total energy (kcal/mol)	70.54	82.82	60.56	74.58

For each compounds C and D, its conformer 1 is the most thermodynamically stable (lowest in energy). In Table 4 below, they are compared in greater detail to explain why conformer 1 of isomer D is more stable than conformer 1 of isomer C.

Table 4: Relative energies of the conformer 1 of C and D.

Property	C conformer 1	D conformer 1
Stretch (kcal/mol	7.71	7.59
Bend (kcal/mol	28.31	18.82
Stretch-bend (kcal/mol	-0.07	-0.14
Torsion (kcal/mol	0.10	0.27
Van der Waals (kcal/mol	33.23	33.23
Electrostatic interactions (kcal/mol	0.30	-0.05
Total energy (kcal/mol	70.54	60.56

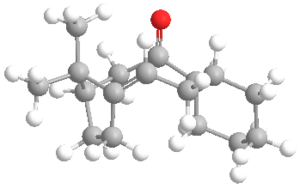
The 3D molecular structure of the most stable conformer of species C and D is shown below:

Molecule C Chair conformer 1

Molecule D Chair conformer 1

Figure 8: Bond angle of the carbonyl carbon center for conformer 1 of C.

Figure 9: Bond angle of the carbonyl carbon center for conformer 1 of D.

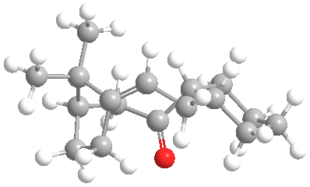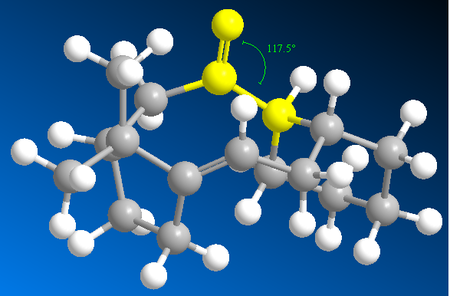
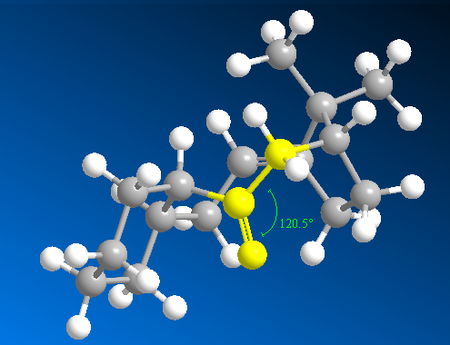
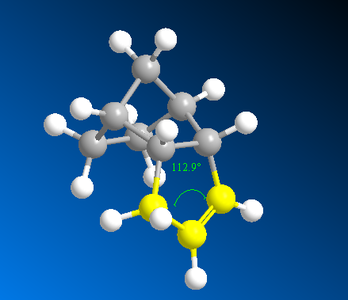
Studying Table 4, it is clear the energy parameter with the largest difference between molecule C and D is the bending term (the deviation from optimal bond angles). The bending term is 9.49 kcal/mol lower for conformer 1 of D than conformer 1 of C. This suggests that the bonding angle for conformer 1 of D is closest to optimal angle thus the overall energy of the molecule is lower since the angle strain is lower (and thus less repulsion from steric clashing). The optimal bond angle for the carbonyl carbon (sp² hybridised) is 120°. For conformer 1 of D, the bond angel for this carbon is 120.5° (Figure 9) and for conformer 1 of C it is 117.5° (Figure 8).

Hyperstable alkenes are a class of molecules which are less reactive than the more ‘traditional’ alkenes. They have less strain than their corresponding parent hydrocarbon (and therefore negative Olefinic Strain Values – a measure of strain which is calculated by taking the difference between the strain energy of the alkene and its parent hydrocarbon). This reduced reactivity is not because of steric hindrance or a stronger π-bond but because of a cage structured (resulting in unfavourable H-H interactions which make the double bond unreactive) and the greater strain of the parent alkane. To prove this statement, the bending and torsional energies of the parent cycloalkane of isomers C and D were calculated.

The bending term increases by 3.75 kcal/mol (from 28.31 to 32.06 kcal/mol) going from isomer C (conformation 1) to its parent alkane and by 5.83 kcal/mol (from 18.82 to 24.65 kcal/mol) going from isomer D to its parent alkane. Similarly, for the torsional term, the torsional strain increases by 9.35 and 8.42 kcal/mol for isomer C and D respectively.

These increases in the bending term for the parent alkanes can be shown by studying the 3D molecular structures of the parent alkanes. The bond angles at where the alkene was positioned before hydrogenation were measured. The bond angles for isomer C and D were 117.3° and 123.7° respectively. The optimal bond angle for a sp³ hybridised carbon (alkane carbon) is 109.5°, therefore these bond angles are very unfavourable thus causing considerable strain in the molecule.

Furthermore, there are also unfavourable Van der Waals (VDW) interactions between the vicinal hydrogens in the parent alkanes because the structure is ‘cage-like’.

Spectroscopic Simulation using Quantum Mechanics

Figure 10: Molecule 17, a derivative of Molecule C.

In this part of the experiment, molecule 17 (Figure 10, DOI:10042/25789 ) was drawn, its structure was optimised (using MMFF94s force field) and then using GaussView, the proton and carbon NMR of the species was predicted (Figure 11 and 12 respectively). Finally, the calculated NMR spectrums were compared with literature to test the legitimacy of quantum mechanically deriving an NMR spectrum.

Figure 11: Calculated ¹H NMR of Molecule 17.

Figure 12: Calculated ¹³C NMR of Molecule 17.

Table 5: Calculated ¹H NMR of 17 compared with literature values.

QM calculated δ/ppm	Literature δ/ppm (Extra comments)
5.23	4.84 (dd,J=7.2,4.7Hz, 1 H)
3.43-3.23	3.40-3.10(m,4H
3.08	2.99(dd,J=6.8, 5.2 Hz, 1 H)
2.83-1.57	2.80-1.35 (series of m, 14 H)
1.17	1.38 (s, 3 H)
1.07	1.25 (s, 3 H)
1.05-1.02	1.10 (s, 3 H)
0.71	1.00-0.80 (m, 1 H)

Table 6: Calculated ¹³C NMR of 17 compared with literature values.

QM calculated δ/ppm	Literature δ/ppm
206.36	218.79
135.05	144.63
115.13	125.33
81.67	72.88
51.13	56.19
47.89	52.52
43.16	48.50
42.00	46.80
36.93	45.76
34.77	39.80
34.62	38.81
29.91	35.85
22.71	32.66
21.76	28.79
21.46	28.29
18.91	26.88
17.56	25.66
16.60	23.86
15.81	20.96
10.12	18.71

Table 5 shows that the difference between the quantum mechanically derived proton chemical shifts and the chemical shifts taken from literature were not so large. Therefore, the values calculated using Gaussian produced somewhat accurate results. Furthermore (further confirming the accuracy of the results) from the table, the protons that are greatly deshielded (have a high chemical shift) are those which are attached to an electron withdrawing group; such as the proton (δ = 3.43-3.23 ppm) attached to a carbon which is attached to a sulphur atom. Or the proton (δ = 5.23) attached to the double bond.

Although the proton NMR yielded good results, the same can’t be said for the carbon NMR. The difference between the predicted chemical shifts and those chemical shifts of literature exceeds more than 5 ppm. This suggests that the conformation of molecule 17 used for the quantum mechanical calculations was different from the conformation of molecule 17 used experimentally in the literature report. However, another possibility is that the predicted chemical shifts or the chemical shifts stated in literature were not accurate.

In molecule 17, three carbon atoms are attached to a(or two) ‘heavy’ sulphur atom(s), and as a result the chemical shifts for these specific carbon atoms need to be corrected (need correction for spin-orbit coupling errors). However since the correction value for a carbon attached to a sulphur is not known and the results produced are far from literature values (therefore likely to be inaccurate), no such corrections where performed.

Though the chemical shifts of the calculated carbon NMR were not similar to those of literature, the carbon’s chemical shifts were in the right order. For example, the first three carbon atoms which had the highest chemical shifts (deshielded the most) were the atoms bonded to the electronegative oxygen atom (in the carbonyl bond) and to the double bond. These chemical shifts were 218.79, 144.63, 125.33 ppm respectively. Other carbons with high chemical shifts included the carbon attached to two (more electronegative) sulphur atoms (δ = 72.88 ppm) and the tertiary and quaternary carbons.

One possible reason why the hydrogen NMR was more accurate than the carbon NMR could be that the hydrogen atom is much smaller in size and therefore the quantum mechanical calculations are easier to perform and more accurate (due to less approximations).

Part Two: Analysis of the properties of the synthesised alkene epoxides

The crystal structures of Shi and Jacobsen catalysts

Figure 13: Synthetic pathway to an asymmetric epoxide using Shi catalyst.

Figure 14: Synthetic pathway to an asymmetric epoxide using Jacobsen catalyst.

Shi and Jacobsen are both asymmetric epoxidation catalysts. Shi asymmetric epoxidation of olefins require oxone and a fructose-derived catalyst. It is notable because it does not require a metal catalyst. Whereas Jacobsen asymmetric epoxidation uses Jacobsens catalyst which is salen-type ligands coordinated to a manganese metal centre.

Figure 13 shows the synthetic pathway to an asymmetric epoxide as described by Hanks et al. Species E is the precursor to Shi’s catalyst and F is the activated catalyst which was generated from persulfuric acid.

Figure 14 shows the synthetic pathway to the asymmetrical epoxidation of cis-alkenes which was adapted by Hanson. Species G is the precursor to Jacobsen’s catalyst and H is the activated catalyst generated from hypochlorite.

Figure 15: Precursor of Shi catalyst, E

Figure 16: Precursor of Jacobsen's catalyst, G

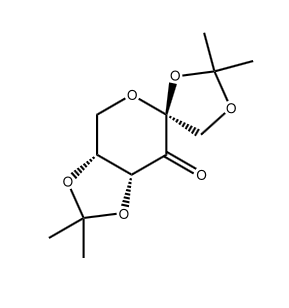
The structures of species E and G (the precursors to Shis and Jacobsens catalysts respectively) were found in the Cambridge Crystal database (using the program ConQuest) and then analysed using Mercury. Species E, as shown in Figure 15, has two anomeric centres. Fructose, a monosaccharide, can exist in linear or ring forms. When in the ring form, a hydroxyl group can react with a carbonyl group to form a ketal group (fructose is a type of ketose). The hydroxyl group can attack the carbonyl group from above or below therefore there are a possible of two anomers, and the anomeric center is the carbon where the carbonyl group was.

In Figure 15, in both of the anomeric centers the two C-O bond lengths are different from each other. At one anomeric center, one C-O bond length is 1.456Å whereas the other is 1.428Å. Similarly at the other anomeric center, one C-O bond length is 1.454Å and other is 1.423Å. This is a difference of 0.028Å and 0.031Å respectively. Since one bond is shorter than the other, it suggests that due to orbital interactions, one bond is becoming weaker whilst the other is becoming stronger. Bond weakening is caused by the oxygen atom of the stronger shorter bond donating its lone pair of electrons into the other C-O σ* orbital. Since electron density is going into an antibonding orbital, the bond order of the C-O decreases, therefore the bond lengthens and becomes weaker.

Figure 16 shows intramolecular interactions between the methyl groups of the tert-butyl groups attached to the benzene rings. Whether these interactions are favourable or unfavourable depends on the distance separating the methyl groups (or more specifically the distance between the hydrogens on the methyl groups) and the sum of the van der Waals radii of the two hydrogens. In Figure 16, the smallest distance separating two hydrogens is 2.421Å. The total sum the van der Waals radii of two hydrogens is ~2.40Å. If the distance between the two hydrogens is similar or smaller than this value, then there is a repulsion interaction between the hydrogen atoms (repulsive electron interactions). Since all the H-H distances in Figure 16 are greater than 2.40Å except the smallest distance, most hydrogen interactions are attractive.

The .log file of the calculations also yielded the free energy ΔG:

ΔG (Hartree) of molecule 17 = -1651.46

The calculated NMR properties of Styrene oxide and trans-Stilbene oxide

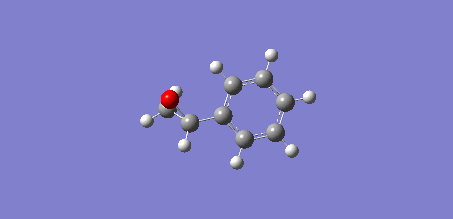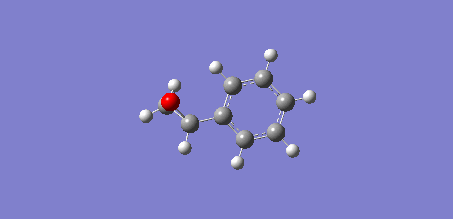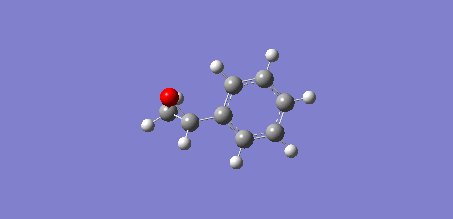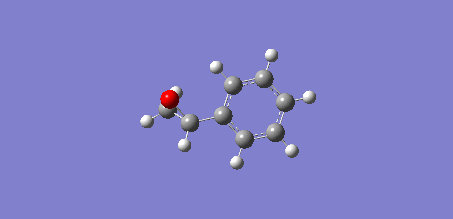
Figure 17 shows a molecule of Styrene or more technically vinyl benzene. This colourless oily liquid is the precursor to polystyrene and many other polymers due to the presence of the vinyl group (allows polymerisation).

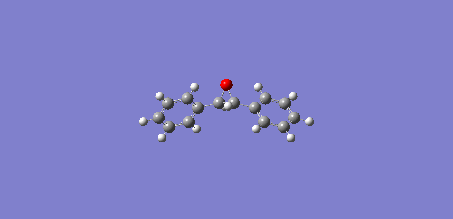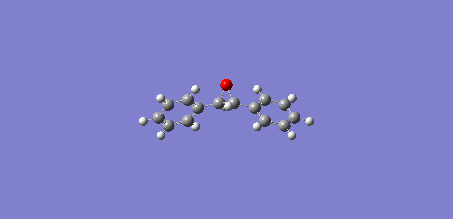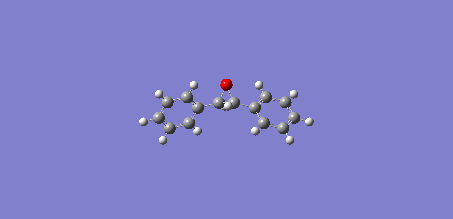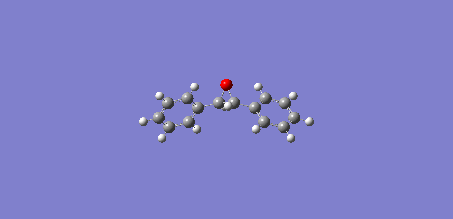
Figure 18 shows a molecule of trans-stilbene, a type of diarylethene.

Figure 17: Molecule of styrene.

Figure 18: Molecule of trans-stilbene.

Figure 19 and 20 show styrene oxide (DOI:10042/25790 ) and trans-stilbene oxide (DOI:10042/25791 ) respectively, the products of styrene and trans-stilbene after epoxidation using either a Shi or Jacobsen catalyst.

Figure 19: Molecule of styrene oxide.

Figure 20: Molecule of trans-stilbene oxide.

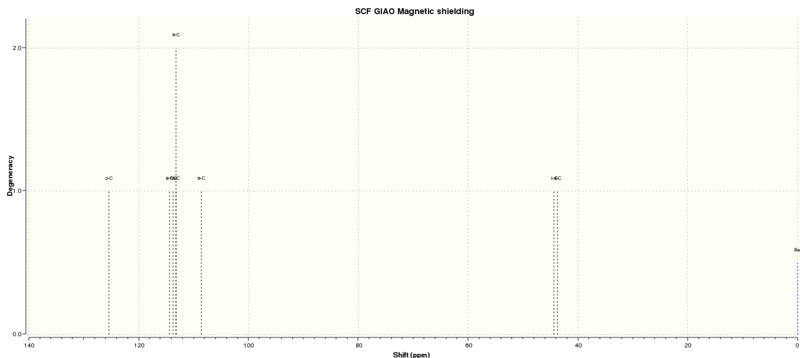
The calculated using quantum mechanics ¹H and ¹³C NMR spectrums of Styrene oxide is shown below:

Figure 21: Predicted ¹H NMR of styrene oxide.

Figure 22: Predicted ¹³C NMR of styrene oxide.

Table 7: Calculated ¹H NMR of styrene oxide compared with literature values.

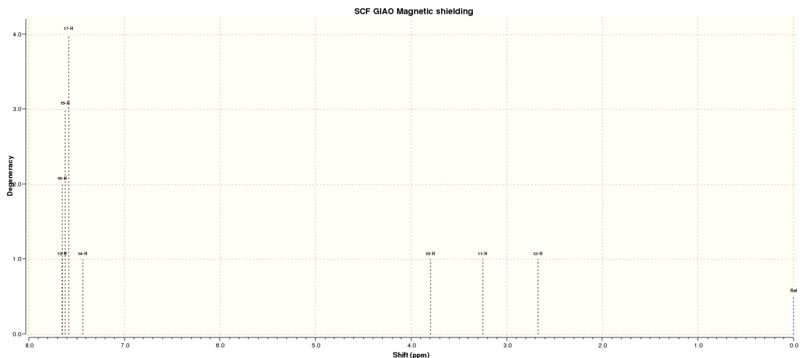
Proton Letter	QM calculated δ/ppm	Literature δ/ppm (Extra comments)
A	7.43-7.65	7.29-7.39 (5H, m, Ar)
B	3.80	3.88 (2H, dd, J1 = 3.8, J2 = 2.7, OCH)
C	3.25	3.17 (1H, dd, J1 = 5.4 Hz, J2 = 4.1 Hz, OCH2)
D	2.67	2.80 (1H, dd, J1 = 5.5 Hz, J2 = 2.6 Hz, OCH2)

Table 8: Calculated ¹³C NMR of styrene oxide compared with literature values.

Carbon Letter	Predicted chemical shift/ppm	Literature chemical shift/ppm
A	125.43	137.6
B	113.71-114.43	128.5
C	113.25	128.2
D	108.57	125.5
E	44.35	52.3
F	43.77	51.2

The calculated using quantum mechanics ¹H and ¹³C NMR spectrums of trans-Stilbene oxide is shown below:

Figure 23: Predicted ¹H NMR of trans-Stilbene oxide.

Figure 24: Predicted ¹³C NMR of trans-Stilbene oxide.

Table 9: Calculated ¹H NMR of trans-stilbene oxide compared with literature values.

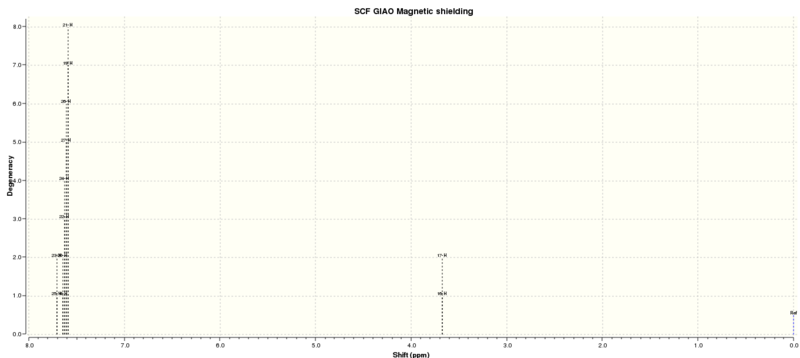
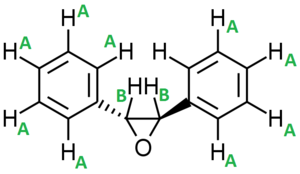
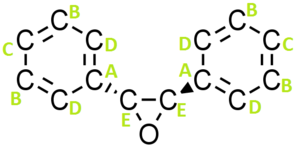
Proton Letter	QM calculated δ/ppm	Literature δ/ppm (Extra comments)
A	7.59-7.71	7.40-7.55 (s, 2H)
B	3.67	3.95 (m, 10H)

Table 10: Calculated ¹³C NMR of trans-stilbene oxide compared with literature values.

Carbon Letter	QM calculated δ/ppm	Literature δ/ppm
A	137.1	124.38
B	128.5	114.52-113.81
C	128.2	113.51
D	125.5	113.37-108.56
E	62.7	56.72

Assigning the absolute configuration of Styrene and Trans-stilbene

The reported literature for optical rotations

There are two enantiomers of Styrene oxide (Figure 25) because there is a chiral center at the carbon attached to the epoxide functional group: (R)-styrene oxide and (S)-styrene oxide.

Similarly there are two enantiomers of trans-Stilbene oxide (Figure 26) because there is a chiral center at the carbons attached to the epoxide functional groups: (R,R)-trans-stilbene oxide and (S,S)-trans-stilbene oxide.

The optical rotations (at wavelength 568 nm) for (R)-styrene oxide and (R,R)-trans-stilbene oxide was found in literature:

(R)-styrene oxide: [α]_D²⁰ = -19.5° (c 1, C_HCl₃, ee> 99%)

(R,R)-trans-stilbene oxide: [α]_D²⁷ = +310° (c 2.5, C₆H₆, ee= 98%)

The calculated chiroptical properties of the product

Optical Rotation (OR)

Figure 25: Enantiomers of Styrene oxide.

Figure 26: Enantiomers of trans-Stilbene oxide.

Table 11: Calculated optical rotation power of Styrene oxide at 589 nm.

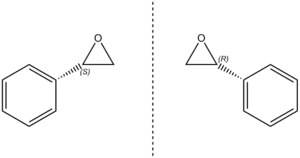
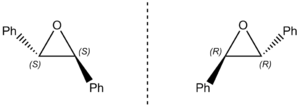
Enantiomer	Optical rotation (°)
(R)-Styrene oxide	-30.42
(S)-Styrene oxide	+30.42

Table 12: Calculated optical rotation power of trans-Stilbene oxide at 589 nm.

Enantiomer	Optical rotation (°)
(R,R)-trans-Stilbene oxide	+304.60
(S,S)-trans-Stilbene oxide	-304.60

This method for calculating optical rotation (Gaussian) for a specific enantiomer becomes increasingly unreliable for values [α]_D < 100°. Hence why the calculated optical rotation of trans-stilbene oxide is very similar to its literature value and its two enantiomers have exactly the same degree of optical rotation (how much they can turn the plane of linearly polarised light) though opposite signs (opposite directions of rotation). Whereas the calculated optical rotation for styrene oxide is not as close to its literature value even though its two enantiomers have exactly the same degree of optical rotation.

Electronic Circular Dichroism (ECD) Spectrum

The UV/Vis and ECD spectrums of Styrene oxide:

Figure 27: UV/Vis spectrum of Styrene oxide.

Figure 28: ECD spectrum of Styrene oxide.

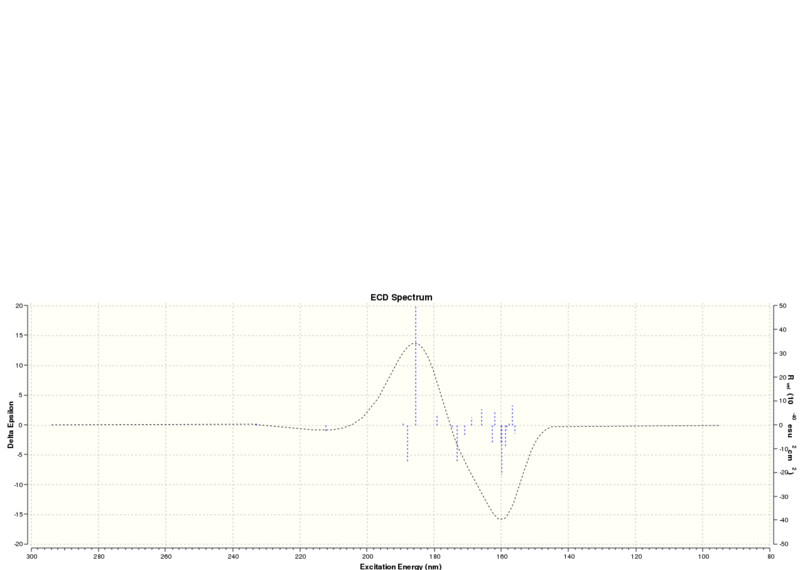
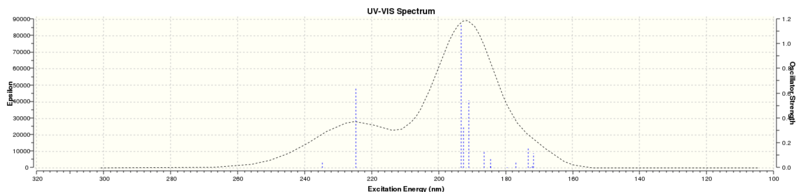
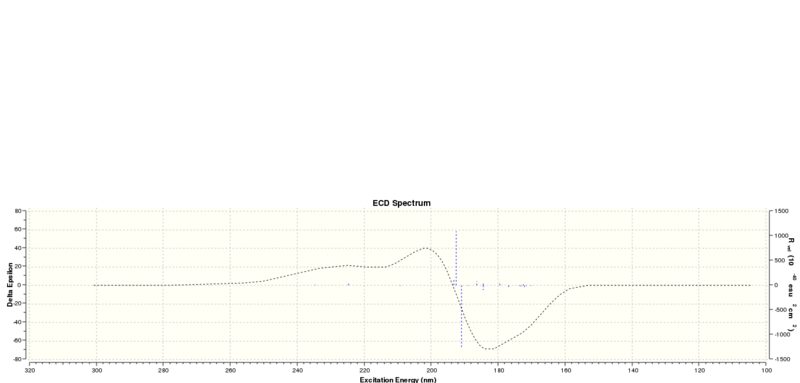
The UV/Vis and ECD spectrums of trans-Stilbene oxide:

Figure 29: UV/Vis spectrum of trans-Stilbene oxide.

Figure 30: ECD spectrum of trans-Stilbene oxide.

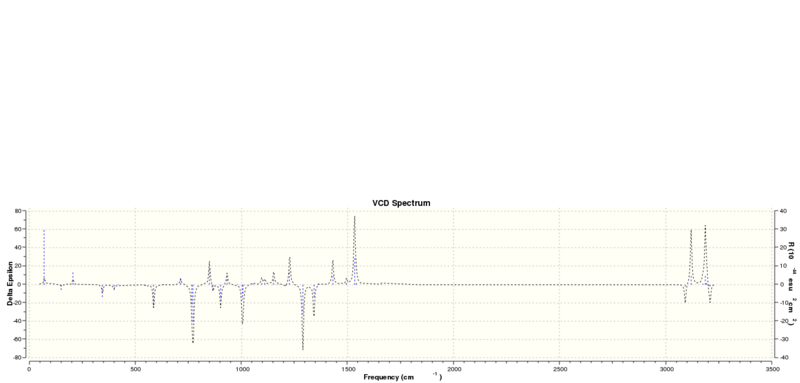
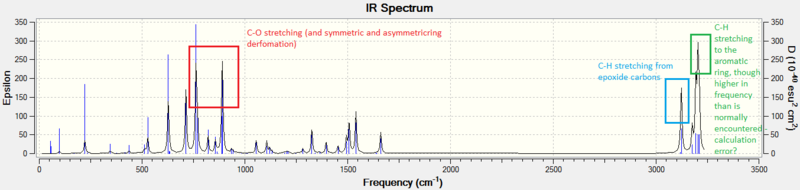
Vibrational circular dichroism (VCD) spectrum

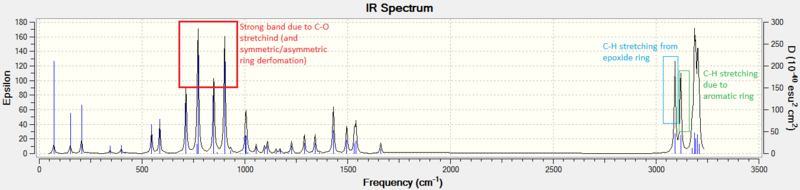
The IR and VCD spectrums of Styrene oxide:

Figure 31: IR spectrum of Styrene oxide. For unlabelled version click here.

Figure 32: VCD spectrum of Styrene oxide.

The IR and VCD spectrums of trans-Stilbene oxide:

Figure 33: IR spectrum of trans-Stilbene oxide. For unlabelled version click here.

Figure 34: VCD spectrum of trans-Stilbene oxide.

Below are animations of the vibrations in Styrene oxide (left) and trans-Stilbene oxide (right):

Using the calculated properties of transition state for β-methyl styrene

Shi catalyst

In this part, the energies of eight different transition states for the reaction between β-methyl styrene and Shi catalyst is studied to predict the major epoxide product – either the (R,R)- or (S,S)- enantiomer. There are several factors which give rise to the eight possible transitions states: whether the product is (R,R)-epoxide or (S,S)-epoxide, which of the two dioxirane oxygens (non-equivalent) in the catalyst is transferred and the whether the orientation of the phenyl group (in the product) is endo- or exo- with respect to the catalyst. The transition states are studied because the epoxidation reaction is kinetically controlled therefore the major enantiomeric product is formed through the pathway with the lowest energy transition state.

The quantum mechanical based calculations for the lowest transition state energies for each the (R,R)- and (S,S)- enantiomers is shown below in Table 13. Each energy value was corrected for entropy and zero-point thermal energies and also for solvation (water is solvent).

Table 13: The energies of the lowest transition states (TS) for Shi epoxidation of β-methyl styrene.

Free energy for (R,R)-TS (Hartree)	Free energy for (S,S)-TS (Hartree)	ΔG (Hartree)	ΔG (kJ/mol)
-1343.032443	-1343.024742	-0.007701	-20.218977

The energy difference between the two enantiomeric transition states was converted to K (the concentration ratio of the two enantiomers, [R]/[S]):

$$\begin{gathered} \mathrm{\Delta }G \\ =-RT\ln K \end{gathered}$$

Rearrange, $K=exp(-\mathrm{\Delta }G/RT)$

$K=exp\frac{(-(-20.2190\times 10^3))}{(8.3144\times 298)}\approx 3499.7$

$[R]$ = concentration of (R,R)-epoxide
$[S]$ = concentration of (S,S)-epoxide

$\text{Enantiomeric excess}(ee\mathrm{\%})=(R\mathrm{\%}-S\mathrm{\%})=\frac{([R]-[S])}{([R]+[S])}=\frac{([R]/[S]-1)}{(R]/[S]+1)}=\frac{(K-1)}{(K+1)}$

$ee=\frac{(3499.7-1)}{(3499.7+1)}\approx 0.99942=99.94\mathrm{\%}$

The enantiomeric excess of (R,R)-epoxide is over 99.94% therefore it is the major product for the reaction between β-methyl styrene and Shi catalyst. This calculated value for enantiomeric excess agrees with literature (ee=95.5%).

Jacobsen catalyst

Similarly, the transition state energies are studied for the reaction between cis-β-methyl styrene and Jacobsen catalyst to predict the major product: (R,S)-epoxide or (S,R) epoxide. There are four possible transition states (catalyst has a fixed chirality) that is dependent on whether the enantiomeric product is (R,S)-epoxide or (S,R) epoxide and whether the orientation of the substrate is endo- or exo- with respect to the catalyst.

The quantum mechanical based calculations for the lowest transition state energies for each the (S,R)- and (R,S)- enantiomers is shown below in Table 14. Also, the calculated enantomeric excess for (S,R)-epoxide is also shown in Table 14.

Table 14: The energies of the lowest transition states for Jacobsen epoxidation of cis-β-methyl styrene.

Free energy for (S,R)-TS (Hartree)	Free energy for (R,S)-TS (Hartree)	ΔG (Hartree)	ΔG (kJ/mol)	K = [S,R]/[R,S]	Enantiomeric Excess (ee)	ee%
-3383.259559	-3383.251060	-0.008499	-22.314126	≈ 8151.900000	≈ 0.999755	99.975000%

The enantiomeric excess of (S,R)-epoxide is over 99.97% therefore it is the major product for the reaction between cis-β-methyl styrene and Jacobsen catalyst. This calculated value for enantiomeric excess is similar to literature (ee=92%).

Investigating the non-covalent interactions in the active-site of the reaction transition state

A NCI was performed on the (R,R)-epoxide transition state with the third lowest transition state energy (DOI:10.6084/m9.figshare.738028 ).

Figure 35: NCI analysis.

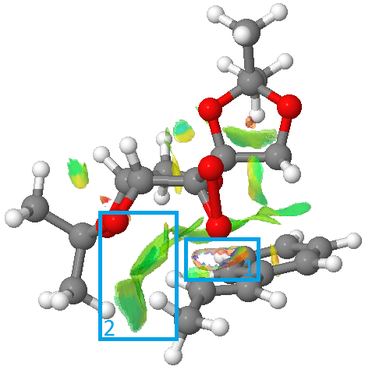
Orbital

Studying Figure 35, right, box 1 shows bond forming in the transition state (between one of the dioxirane oxygen atoms and the double bond in β-methyl styrene). This interaction can loosely be described as ‘half-covalent’ and therefore it is not NCI.

Box 2 indicates a reasonably attractive non-covalent interaction (van der Waals) between the oxygen atoms attached to the anomeric carbon on the Shi catalyst and the hydrogens on the methyl group on β-methyl styrene.

Investigating the Electronic topology (QTAIM) in the active-site of the reaction transition state

QTAIM is similar to NCI however as well as identifying ‘weak’ non-covalent interactions, QTAIM also concentrates on the electron density in the ‘strong’ covalent regions of molecule.

The transition state used for QTAIM analysis was the same used for NCI analysis: (R,R)-epoxide transition state with the third lowest transition state energy.

Figure 36 shows different types of bond critical points (BCPs).

Figure 36: QTAIM analysis on a transition state for the Shi epoxidation of β-methyl styrene. For a non-labelled version of this image, click here

The blue box shows an example of an interaction between covalent bonds. The red boxes show examples of ‘weaker’ interactions e.g. van der Waals.

The atom in the middle of box 1 (blue) is one of the anomeric carbon atoms present in the Shi catalyst. This carbon is bonded to two methyl groups and two oxygen atoms. The BCP for the carbon-oxygen bond is off-centre and is closer to the carbon atom. This suggests the covalent bond has some ionic properties (it is polarised due to the electronegative oxygen atom).

Box 2 (red) shows an interaction between the hydrogen of the catalyst and the phenyl group of the β-methyl styrene. (BCP is closer to the hydrogen.)

Box 3 (red) shows an interaction between an oxygen atom of the catalyst and a hydrogen atom in the methyl group of β-methyl styrene. (BCP is closer to the hydrogen since the oxygen atom is very electronegative.)

Box 4 (red) shows an interaction between a hydrogen atom of the catalyst and a carbon in the alkene bond of β-methyl styrene. (BCP is halfway between the two atoms.)

Suggesting new candidates for investigations

Reaxy was used to search for a different epoxide with an optical rotation >500 or <-500. The following command was inputted in the advanced search box:

ORP.ORP<'-500' or ORP.ORP>'500'

However the search did not yield many suitable results, therefore the following options were set in the standard search box:

And from it, one possible epoxide which can be used for computational experiments: Pulegone epoxide.

Figure 37: Pulegone and pulegone epoxide

Pulegone

The optical rotations (at wavelength 324 nm) for Pulegone oxide found in literature:

cis R-(+)-pulegone oxide: [α]_D²⁵ = +853.9° (c 0.03, EtOH)

Pulegone occurs naturally in nature (found in a variety of plants) and both pulegone and pulegone epoxide can be obtained from chemical suppliers.