Rep:Mod:Enrique's wiki page 1234
Gaussian can be used to model a wide variety of molecules and can provide information on their optimised structure, bond length, bond angles, vibration frequencies, molecular orbitals and many other things. This makes it an ideal tool for chemists to use when they want to quickly and easily simulate a molecule. In this wiki, I'll be using Gaussian to determine numerous properties of NH3, N2, H2 and ClF including charges, MO's and bond lengths.
Note: All bond lengths were set to 1.3 Å before an optimisation was carried out.
NH3 molecule
Calculation method:
RB3LYP
Basis set:
6-31G(d,p)
Final energy E(RB3LYP):
-56.55776873 a.u.
RMS gradient:
0.00000485 a.u.
Point Group:
C3V
Optimised N-H Bond length:
1.01798 Å
Literature value of N-H bond length
A literature value was found which recorded the experimentally determined N-H bond length as 1.012 Å [1] . Compared to our calculated bond length there is only an error of +0.59% since the optimised length is slightly larger than our experimental value, but is a small error (less than 1%) regardless. As a result I would say the 6-31G(d,p) basis set provides a good approximation of the bond length in this case.
Optimised H-N-H bond angle:
105.741°
Literature value of H-N-H bond length
A literature value was also found which recorded the experimentally determined H-N-H bond angle as 106.7° [1] . Compared to the calculated bond angle there is an small error of -0.899% since the optimised value slight underestimates the angle compared to the experimental value. However, this error is still less than 1% and so I still believe that the 6-31G(d,p) basis set provides a good approximation of the bond angle in this case.
Item table
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES Predicted change in Energy=-5.986272D-10
Optimisation file
The optimisation file is linked to here
Jmol image
Optimised NH3 |
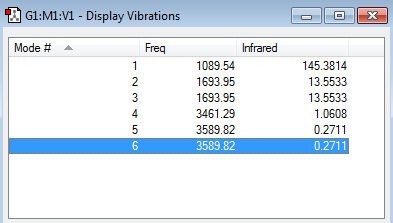
Vibration frequency table
Modes from the 3N-6 rule:
(3x4)-6 = 6 modes
Degenerate modes:
2 and 3 are degenerate, 5 and 6 are degenerate
Bending vibrations:
1,2,3
Bond stretch vibrations:
4,5,6
Highly symmetric mode:
4
Umbrella mode:
1
Number of bands in the experimental spectrum of gaseous ammonia:
2 bands would appear in spectra which are caused by modes 1, 2 and 3. These are the only modes that appear because the other modes are very low in intensity relative to these three and so wouldn't clearly be visible in the spectra. Also modes 2 and 3 are degenerate so they would appear as one band in the spectra (since their frequencies would also be the same), meaning we'd see 2 bands in total on our output.
Charges of N and H
N-atom charge: -1.125
H-atom charge: +0.375
I would expect the Nitrogen to have a negative charge and the Hydrogen to have a positive charge because I know Nitrogen is more electronegative than Hydrogen, meaning the electron density should lie closer to the Nitrogen atom compared to the hydrogen atoms since Nitrogen would attract the electrons away from them. This also explains the hydrogen's positive charge as the electrons would spend less time there and so, relative to the Nitrogen, the hydrogen atoms would have an overall positive charge.
N2 molecule
Calculation method:
RB3LYP
Basis set:
6-31G(d,p)
Final energy E(RB3LYP):
-109.52412868 a.u.
RMS gradient:
0.00000365 a.u.
Point Group:
D∞H
Optimised N-N Bond length:
1.10550 Å
Literature value of N-N bond length
A literature value of 1.09768 Å[2] was found for the N-N bond. Compared to this experimental value, the optimised value only deviates from it by -0.71% since the optimised value slightly overestimates the bond length in this case. This error is less than 1% and so I believe that the 6-31G(d,p) basis set has provided a good approximation of this bond length once again.
Item table
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000006 0.000300 YES Maximum Displacement 0.000002 0.001800 YES RMS Displacement 0.000003 0.001200 YES Predicted change in Energy=-1.248809D-11
Optimisation file
The optimisation file is linked to here
Jmol image
Optimised N2 |
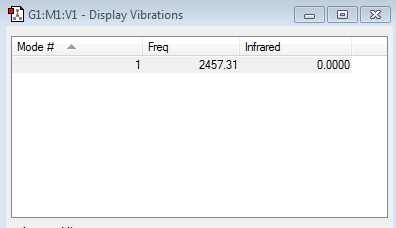
Vibration frequency table
As expected, only 1 vibrational mode is present (as predicted by the 3N-5 rule, which gives 1 when N=2) and no negative frequencies are present. This mode is not visible in the IR spectra of N2 however as it involves a symmetric stretch, which won't cause a change in the dipoles since both the Nitrogen atoms have the same electronegativity and so won't appear as a result.
H2 molecule
Calculation method:
RB3LYP
Basis set:
6-31G(d,p)
Final energy E(RB3LYP):
-1.17853930 a.u.
RMS gradient:
0.00012170 a.u.
Point Group:
D∞H
Optimised H-H Bond length:
0.74309 Å
Literature value of H-H bond length
A literature value of 0.74 Å[3] was found for the H-H bond. Compared to this experimental value, the optimised value only deviates from it by -0.42% since the optimised value slightly overestimates the bond length in this case. This error is still less than 1% however, therefore I believe that the 6-31G(d,p) basis set has provided a good approximation of this bond length.
Item table
Item Value Threshold Converged? Maximum Force 0.000211 0.000450 YES RMS Force 0.000211 0.000300 YES Maximum Displacement 0.000278 0.001800 YES RMS Displacement 0.000393 0.001200 YES Predicted change in Energy=-5.852867D-08
Optimisation file
The optimisation file is linked to here
Jmol image
Optimised H2 |
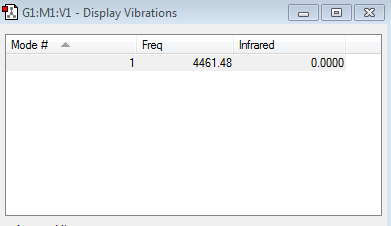
Vibration frequency table
Similar to N2, only 1 vibrational mode is present (as predicted by the 3N-5 rule, which gives 1 when N=2) and no negative frequencies are present. This mode is not visible in the IR spectra of N2 however as it also involves a symmetric stretch, which won't cause a change in the dipoles in this case since both the Hydrogen atoms have the same electronegativity and so won't appear as a result.
Reaction energy of Haber-Bosch process
The reaction is: N2 + 3H2 -> 2NH3
E(NH3)= -56.55776873 a.u
2*E(NH3)= -113.11553746
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853930 a.u.
3*E(H2)= -3.5356179
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579088 a.u.
ΔE*2625.5= -146.478966598 kJ/mol, which is -146.48 kJ/mol when rounded to 2 d.p
The ammonia product is more stable because the total energy released when forming the NH bonds is slightly greater than the total energy required to break the N2 and H2 bonds, making the ammonia more thermodynamically stable therefore.
Project molecule: ClF
Calculation method:
RB3LYP
Basis set:
6-31G(d,p)
Final energy E(RB3LYP):
-559.94269589 a.u.
RMS gradient:
0.00001254 a.u.
Point Group:
C∞V
Optimised Cl-F Bond length:
1.66392 Å
Literature value of Cl-F bond length
A literature value was obtained for the Cl-F bond which listed it as 1.628 Å [4]. Compared to the this value, the optimised value has an error of +2.2% which is slightly greater than the previous errors which I calculated. This suggests that the 6-31G(d,p) basis set doesn't provide as good an approximation for this bond compared to other diatomic molecules such as H2 or N2 and is probably related to how gaussian considers the electronegativity of each atom when modelling the bond (since this can cause the bond length to shorten).
Item table
Item Value Threshold Converged? Maximum Force 0.000022 0.000450 YES RMS Force 0.000022 0.000300 YES Maximum Displacement 0.000038 0.001800 YES RMS Displacement 0.000054 0.001200 YES Predicted change in Energy=-8.279391D-10
Optimisation file
The optimisation file is linked to here
Jmol image
Optimised ClF |
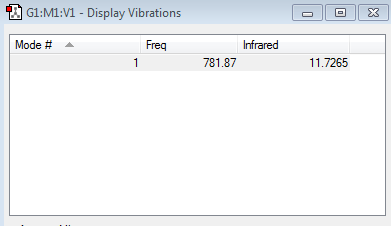
Vibration frequency table
ClF has only 1 vibrational mode (as predicted by the 3N-5 rule, which gives 1 when N=2) and has no negative frequencies. Unlike N2 and H2 however, this mode is visible in the IR spectra of ClF because it involves a symmetric stretch which causes a change in the molecule's dipoles since Fluorine has a higher electronegativity than Chlorine, causing it to appear as a result.
Charges of Cl and F
Cl-atom charge: +0.309
F-atom charge: -0.309
Molecular Orbitals
Molecular Orbital 1
This image shows the σ Molecular orbital between the 2s and 3s orbitals in Fluorine and Chlorine respectively and is occupied by electrons. The resulting MO is bonding and has an energy of -1.21878 a.u, which is the deepest in energy out of all the orbitals I have listed in this section and is probably too low for the molecule to be considered as a possible HOMO for ClF. This MO would normally result in a σ bond being formed, however because the corresponding σ* orbital is also filled no bond will form as the σ* orbital essentially cancels with the σ orbital.
Molecular Orbital 2
This image shows the σ* Molecular orbital between the 2s and 3s orbitals in Fluorine and Chlorine respectively and is occupied by electrons. The resulting MO is antibonding and has an energy of -0.83308 a.u, which is low enough for it to be considered a possible HOMO in ClF. As mentioned before, this σ* orbital is filled and so it prevents the corresponding σ bond being formed between the 2s and 3s orbitals in ClF.
Molecular Orbital 3
This image shows the σ Molecular orbital between the 2p and 3p orbitals in Fluorine and Chlorine respectively and is occupied by electrons. The resulting MO is bonding and has an energy of -0.52320 a.u, which is low enough for it to be considered a possible HOMO in ClF. Unlike the 2s-3s MO, this MO does result in a σ bond being formed because the corresponding σ* orbital is not occupied hence the bond will form.
Molecular Orbital 4
This image shows the π Molecular orbital between the 2p and 3p orbitals in Fluorine and Chlorine respectively and is occupied by electrons. The resulting MO is bonding and has an energy of -0.46721 a.u, which is low enough for it to be considered a possible HOMO in ClF. This MO would normally result in a π bond being formed, however because the corresponding π * orbital is also filled no bond will form as the π* orbital will cancel with the π orbital.
Molecular Orbital 5
This image shows the π* Molecular orbital between the 2p and 3p orbitals in Fluorine and Chlorine respectively and is occupied by electrons. The resulting MO is antibonding and has an energy of -0.32851 a.u, which is the highest energy out of all the occupied orbitals and so this suggests that this orbital is most likely to act as the HOMO in ClF. Similar to the σ* orbital, this π* orbital is filled and so it prevents the corresponding π bond being formed between the 2p and 3p orbitals in ClF.
References
- ↑ 1.0 1.1 Chacon-Taylor MR, McCarthy MI. Ab initio based classical electrostatic potentials for the interaction between molecules and surfaces. The Journal of Physical Chemistry. 1996 May 2;100(18):7610-6.
- ↑ Feifel R, Andersson M, Öhrwall G, Sorensen SL, Piancastelli MN, Tchaplyguine M, Björneholm O, Karlsson L, Svensson S. A quantitative analysis of the N 1s→ π* photoabsorption profile in N 2: new spectroscopical constants for the core-excited state. Chemical physics letters. 2004 Jan 8;383(3):222-9.
- ↑ Liang T, Devine B, Phillpot SR, Sinnott SB. Variable charge reactive potential for hydrocarbons to simulate organic-copper interactions. The Journal of Physical Chemistry A. 2012 Jul 19;116(30):7976-91.
- ↑ Boese R, Boese AD, Bláser D, Antipin MY, Ellern A, Seppelt K. The surprising crystal packing of chlorinefluoride. Angewandte Chemie International Edition in English. 1997 Aug 4;36(13‐14):1489-92.