Rep:Mod:Emily1394
Page List
The Calculations Log files can be found here
For main Introduction/conclusion page click here
For Excerise 1 page click here
For Excerise 2 page click here
For Excerise 3 page click here
Third Year Computational Lab Transition States - Emily Brown
Please note each page has its own references at the bottom of the page.
Introduction
Theory
Transition State: This is a maxima on the reaction coordinate graph. At the point the gradient/first derivative is zero and can be referred to as a turning point on the graph.
Potential Energy Surface: This has 3N-6 dimensions and if you travel in one dimension you can draw a reaction coordinate graph as shown below. [1] The PES is a function of energy vs every coordinate. [2]
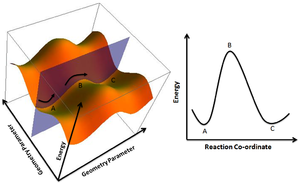
Due to the transition state being a turning point on the reaction coordinate graph it can be found by setting the first derivative to zero as at a minima/maxima the gradient is zero. The potential energy surface allows you to travel in directions which may be away from the reaction coordinate you are trying to locate. The potential energy surface has 3N-6 dimensions.[2] Programs like GuassView take advantage of the fact that all these dimensions are positive in curvature apart from one which is the minimum energy path. This results in an imaginary frequency which is the single negative frequency found in the frequency calculation of a transition state geometry. Energy minimas have zero negative frequencies in their frequency calculations and saddle points have multiple. [2] Nf710 (talk) 22:05, 14 December 2016 (UTC) First order Saddle points (whihc are Tss) only have one negative frequency.
Reactions can be controlled by a number of different factors some of these being sterics and secondary orbital effects. Reactions often compromise between multiple aspects for example a reaction may be sterically disfavored but that particular reaction path could result in good orbital overlap. Secondary oribtal interactions tend to favor the endo-adduct being formed in Diels-Alder reactions.
The reactants tend to form the products via the higher energy transition state which is shown as an energy maximum on the above graph, the energy required to overcome this barrier is known as the activation energy and can be seen in the arrhenius equation as the symbol Ea. The activation energy depends on many factors and programmes like gaussian can be used to estimate this energy and predict whether reactions are likely to occur. For example there are two cis dienes present in the reactant in exercise 3 but only one is involved int he dies alder reactions as the other is known to have a high transition state making it very kinetically unfavourable.
Diels Alder reactions are classified as [4+2] cycloadditions typically between a diene and a dieneophile. The reactions occur via a concerted mechanism with a cyclic transition state. The reaction involves the breaking of 2π bonds and the formation of 2 new σ bonds and a single new π bond. The breaking of the pi bonds is the enthalpic driving force in the reaction as breaking a carbon carbon double bond releases a lot of energy. Cycloaddition reactions have been categorised by Woodward Hoffman to state whether they are thermally or photochemically allowed. Diels-alder reactions can also be classified as normal electron demand or inverse electron demand. Normal electron demand is the case when the HOMO of the diene reacts with the LUMO of the dieneohile, where as inverse electron demand is when the LUMO of the diene reacts with the HOMO of the dieneophile. It has been shown that adding electron donating groups/ electron withdrawing groups to certain positions on the diene/dieneophile can facilitate the Diels-Alder reaction by effecting the energy levels of their HOMO/LUMO thus narrowing the energy gap between the interacting HOMO and LUMO thus facilitating a better orbital overlap.
Cheleotropic reactions is a class of pericyclic reactions which present themselves in exercise 3 which is the cyclic addition of SO2 to a diene. These reactions were exploded in the Woodward and Hoffman's famous publication. [3]
Nf710 (talk) 22:09, 14 December 2016 (UTC) This section was excellent
Computational
Initially structures will be optimized using method1 and then using method2. Doing the initial 'tidy up' allows computational time to be saved. Locating transition states has proved difficult for certain systems which results in different approaches being undertaken such as freezing certain bonds by using the opt=modredundant keywords thus locking atoms together to perform initial optimizations. Another approach is to start from the products or reactants and lengthen certain bonds in an attempt to locate the transition state. Structures were confirmed via frequency calculations: the lack of negative frequencies in the frequency calculation indicates that the structure is optimised to a true minimum, the presence of one negative frequency indicates that a transition state has been reached, more than one negative frequency means that a saddle point structure has been reached. [4]
It proved necessary at times to freeze bonds to locate a transition state however once found all structures were later re-optimised under no symmetry constraints. The int=ultrafine keywords are expressed in the DFT calculations as optimisation with many low level vibration modes will often proceed more reliably when a larger DFT integration grid is requested. [5]
Method 1: Opt+Freq, semi empirical, PM6.
Method 2: Opt+Freq, DFT B3LYP/631G(d).
Both the density function theory (DFT) and semi-empirical methods are able to describe quantum states as many electron systems; they both use the born-opinhiemer approximation where you first solve for the electronic degrees of freedom. [6] In DFT the many-electron wavefunction is completely bypassed in favor of the electron density, the variational principle is used to minimise the energy with respect to electron density. However a key problem with this method is that the energy functional is not know. [6] Semi-empirical Methods are a simplified versions of Hartree-Fock theory using empirical corrections in order to improve performance; these can be preformed prior to DFT calculations in order to save computational time. [7] The PM6 part of the calculation specifics that the PM6 hamiltonian is to use in the semi-empirical calculation. [8]
Notes: When optimising to a transition state I used: TS (Berry), Force constants allowed to calculate once. When optimising to a minimum use: minimum and force constants are allowed to calculate never. Occasional calculations were run on the colleges HPC to save computational time as these servers use more processors than my local computer in college. The 09 version of gaussian suite was used when on windows college computers.
Nf710 (talk) 22:18, 14 December 2016 (UTC) Very nice general overview of the methods. Excellent intro. The first I have given full marks to.
Exercises
Each exercise is contained on its own page which are linked to below and above the contents section of each page. Each page containing an exercise has Jmol files of all structures used in that exercise at the end of the page, they are accompanied by the 'results summary' section of their opt/freq calculation to confirm the existence of the correct number of negative frequencies and to allow the geometry of each structure to be viewed.
Conclusion
The transition states were successfully located for multiple reaction following a similar procedure in each case. Orbital analysis was undertaken and HOMO+1, HOMO, LUMO and LUMO-1 levels were explored. The transition states were be further identified by looking into the IRC, thus allowing endo/exo transition states to be confidently labeled. The IRC also revealed information about the reaction coordinate such that no other intermediates existed and that no other transition states were encountered for our reactions.
This computational lab has also highlighed some key difference between the semi-empirical based basis sets and those of basis sets belonging to the density functional theory family. The lab has drawn attention to the importance of chosen the correct basis set and has given me the ability to use Gaussian programs to confidently locate transition states for reactions and highlighted some key methods to further understand the transition states found such as IRC.
References
- ↑ 1.0 1.1 https://commons.wikimedia.org/wiki/File:Potential_Energy_Surface_and_Corresponding_Reaction_Coordinate_Diagram.png (accessed 23rd November)
- ↑ 2.0 2.1 2.2 Dr. Hunt's year 4 lecture course: "Computational Inorganic Chemistry" Lecture4, Handout3. http://www.huntresearchgroup.org.uk/teaching/teaching_comp_chem_year4/L4_PES.pdf (accessed 25th November 2016)
- ↑ Woodward, R.B.; Hoffman, R. Angew. Chem. Int. Ed. Engl. 1969, 8, 781. DOI:10.1002/anie.196907811
- ↑ Foresman, J. and Frisch, A. (1996). Exploring Chemistry With Electronic Structure Methods: A Guide to Using Gaussian. 2nd ed. Guassian, Chapter 1.
- ↑ http://www.gaussian.com/g_tech/g_ur/k_opt.htm (accessed 25th November 2016)
- ↑ 6.0 6.1 https://www.quora.com/What-is-the-difference-between-density-functional-theory-and-hartree-fock (accessed 25th November 2016)
- ↑ http://www.cup.uni-muenchen.de/ch/compchem/energy/semi1.html (accessed 25th November 2016)
- ↑ http://www.gaussian.com/g_tech/g_ur/k_semiempirical.html (accessed 25th November 2016)
