Rep:Mod:Elizabeth Mogaji MgO

The Free Energy and Thermal Expansion of MgO

Introduction

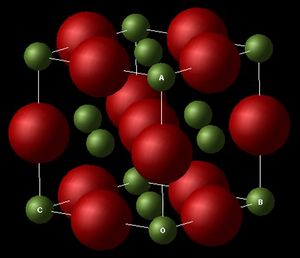
Atomic vibrations can provide various information about a system such as its thermal properties, electronic properties, conductivity, phase transitions and its free energy. In this experiment, the system under study is an ideal, 3D periodic crystal structure of Magnesium Oxide (MgO), represented as a primitive unit cell and as a conventional face centred cubic lattice (fcc).

MgO Primitive Lattice, illustrating the lattice parameters a,b and c.
MgO Conventional Lattice (FCC), Illustrating the lattice parameters a,b and c.

Two approaches would be adopted and compared. A Quasi-Harmonic Approximation (QHA) and Molecular Dynamics (MD). Both models would be used to simulate the vibrations in the crystal, investigate a thermal property of the material as temperature is increased and thus quantify the thermal expansion by calculating the volume thermal expansion coefficient. The QHA uses a simple parabolic function as that of the harmonic oscillator to compute the vibrational modes of MgO whist changing the equilibrium bond displacement in order to minimize the free energy. Contrarily, the MD simulates the actual random motions of the atoms by applying newton’s law of motion, following the trajectories and computing thermodynamic properties as time averages of their behavior.

RedHat Linux, DLVisualize and GULP (General Utility Lattice Program) will be used. These provide an interface for the construction and visualization of the crystal structure as well as the ability to analyse and calculate related thermodynamic properties.

Reciprocal space & k-vectors

A crystal is an infinite repetition of a fundamental unit which exhibits translational periodicity. This periodicity can be transformed under Fourier's theorem as the sum of periodic sine or cosine terms called the Fourier series. In so doing, a crystal lattice in real space is converted to a reciprocal lattice in reciprocal, momentum or k-space, and this is a consistent process as k is defined as 2π/λ, which is the inverse of (wave)length. This transformation is useful as it allows the investigation of real, physical properties; for example, the Fourier coefficients generated are pertaining to scattering intensities in X-ray crystallography. More applicable to this experiment is that this conversion enables us to compute the vibrations within the crystal by associating a k-vector to every possible vibrational mode which describes the propagation of the wave in 3D k-space, allowing us to plot the phonon dispersion curves and the density of states from which we can calculate the free energy of the system and its thermal behavior.

Phonons, Dispersion Curves & Density of States

Vibrations in solid crystals occur in a coupled fashion, due to the spatial positioning of each atom. These collective vibrations are called phonons. They are the discrete unit or quantum of vibrational energy, in the same way a photon is described as a quantum of light energy. Due to the periodic nature of the crystal structure, only one unit cell is required to visualize this vibration as the relative motion of its neighboring cells will be computed to generate the propagating wave. A wave vector k=2π/λ, of a given wavelength can be associated with each of the possible vibrational modes within the system. When λ=0, each unit is moving in the same direction and there is no change in energy, thus this would correspond to the lowest energy vibrational mode, so k=0; when λ= 2a, with a being the lattice spacing, k=π/a, this corresponds to the highest energy vibrational mode as each of the units are moving out of phase with each other.

The wave vector is related to the momentum via, the de Broglie equation, λ=h/p, so k=ħp, likewise if E=hν or ħω (where ω = 2πν - angular velocity) and p=mv we can obtain the kinetic energy, E_k=1/2mv²; seeing that each possible vibration within the crystal has an associated k descriptor, of a given energy, we are able to plot the vibrational frequency as a function of k giving rise to a dispersion curve.

The phonon density of state (DOS) provides the number of states available for a given energy interval. It shares a common frequency axis with the dispersion curve thus allowing conversion between the two.

Computing the Lattice Vibrations (Phonons) of MgO

The phonons are computed along 50 k points in the reciprocal space, this gives rise to a dispersion curve as below.

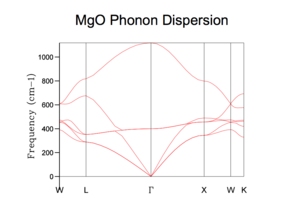
Being a hetero-diatomic, we observe 6 phonon branches in the graph, corresponding to vibrations modes of each atom in the k_x, k_y, k_z direction, consequently, we also observe branches that run downwards to converge at the origin, Γ(0,0,0), which are referred to as the acoustic branch while others that do not converge to Γ are termed optic branch.

In order to simplify the visualization of the phonons in 3D k-space, specific points are chosen, with given k_x, k_y, k_z, values, W, L, Γ, X, K, which possess characteristic symmetry properties. The phonons are computed along the path set out by these points.

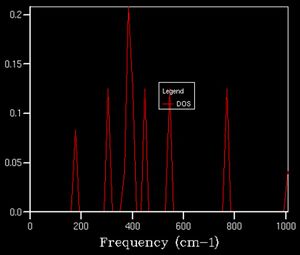
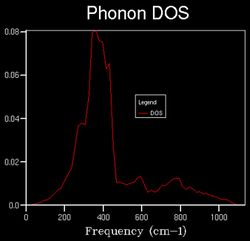
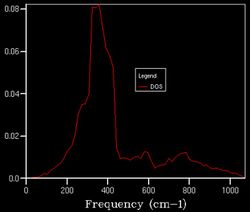
The number of vibrational modes accessible at a given energy (corresponding to a k value) is given by the density of state. For example, the image below indicates the density of states computed from one k point, given by the size of the k-grid we have chosen to sample.

Here we see 4 distinct peaks. The k-point for which this corresponds to is the symmetry position L(0.5, 0.5, 0.5). Upon examining the dispersion curve, we see that 4 branches cross that point with respective frequencies as indicated on the DOS plot; however, the relative intensities of the peaks could be explained by the convergence of two of the bands at that point, analogous to a degenerate state, 2 states present at the same energy.

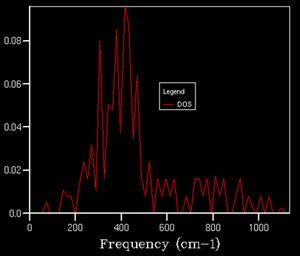
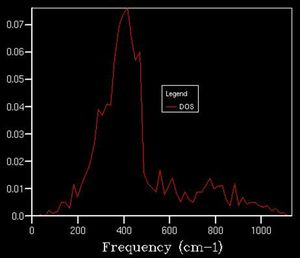
As we increase the k-point grid size, the density of states increases, this is because it allows us more access to the k space so that we can sample a greater number of phonons, giving us a better representation of the distribution of vibrational states available to the system and thus we can better calculate various properties of the system. This effect is illustrated below.

2x2x2
5x5x5
10x10x10
15x15x15
20x20x20
25x25x25
35x35x35

After a grid size of about 15, we can clearly observe a defined shape for the density of state thus this can be used as a suitable approximation to the total DOS. In plots beforehand, there is less of a defined structure to the plot as the structure of the DOS changes significantly, whereas afterwards, the curvature of the plot simply smoothens out without necessarily altering the overall shape.

This optimal grid size would be appropriate for calculation on other materials with the same crystal structure such as Calcuim oxide (CaO) but not on a metal such a body centred cubic Lithium or a Cubic hexoctahedral zeolite such as Faujasite as these possess different crystal structures corresponding to different lattice in the reciprocal space.

The Free Energy - The Harmonic Approximation

The Helmholtz free energy is computed in the quasi-harmonic approximation by summing over all the vibrational modes of the crystal, i.e. over all the k-values. This is achieved in a similar manner as above, and by setting the temperature to 300 K.

The size of the k-grid affects the accuracy of the calculation, so in order to assign the most suitable grid size, the Helmholtz free energy was extracted for runs at increasing grid size and plotted as a graph illustrate this effect and to resolve the grid size at which the free energy remains unaffected, indicated on the graph as the point where it begins to plateau, 18x18x18 (-40.926483).

Seeing that the grid size affects the accuracy of the calculations. Using a grid size of 3x3x3 would give results accurate to 1 meV (-40.926432), 4x4x4 to 0.5 meV (-40.926450), and 5x5x5 to 0.1 meV (-40.926463) thus saving processing power and time of the calculations.

Using the resolved optimal grid size for this system, (18*18*18), would be inappropriate to calculate the free energies for other structures such as CaO, Faujasite or Lithium, as they possess different interatomic potentials.

Thermal Expansion of MgO

QHA

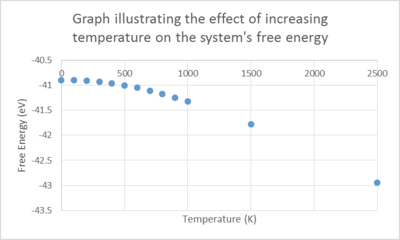
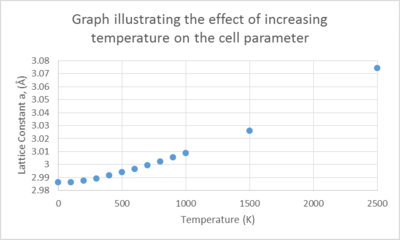
Changes in the free energy and the lattice constant were followed as the temperature was increased from 0 to 1000 K using the optimized grid size as above. The outcome of the experiment is plotted on the graph below.

The trends of these 2 plots are opposing as the temperature is increased. The free energy decreases non – linearly with temperature while the lattice parameter increases with temperature. Under the QHA, the Helmholtz free energy (F) is defined as

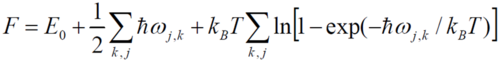
where the first term is the internal energy, the second term, the zero point energy and final term the vibrational entropic contributions (as the solid vibrates, disorder is introduced). The dependence of the entropy on temperature gives rise to the non-linearity observed.

The non-linearity of the lattice parameter plot arises due to the parabolic approximation given by the QHA, relating the lattice constant to the equilibrium ‘bond distance’ between the unit cells. A fundamental flaw in the approximation is that it is only accurate at ‘displacements’ close to the equilibrium value, thus as we increase the temperature towards the melting point of MgO, the computed phonon modes would not represent the reality of the motions of the ions as it does not take into account anharmonicity leading to bond dissociation and consequent break down of the lattice structure.

In a diatomic molecule being modelled by a harmonic potential, as we increase the temperature, thermal excitation of the higher vibrational modes occur resulting in intense vibrations, whilst retaining the equilibrium bond length. It does not allow for changes in the atomic positions. On the contrary, In the QHA, we observe an increase in bond length because the geometry changes in order to minimize the free energy of the system.

As a material is heated, its kinetic energy increases, the increased motion within its molecules generate a greater average separation leading to an expansion of its volume. The degree by which this material has ‘expanded’ in relation to the changes in temperature, is given by the thermal expansion coefficient:

α_{V} = \frac{1}{V} {(\frac{\partial V}{\partial T})}_{p}

This value is dependent on the temperature and vary between materials due to varying bond energies.

The volume thermal expansion of MgO was represented by a second order polynomial to give alpha as 2.20 x 10^-5 K^-1 at 300 K under QHA (using: y = 2E-07x² + 0.0003x +18.809) and 2.79 x 10^-5 K^-1 at 300 K under MD (using: y = 2E-06x² + 0.0155x +597.78), compared to the literature value of around 34 x 10^-6 ± 6% between 77-1315 K^-1.^[1] These values are far from the experimental values. A major approximation being made in the case of the QHA is that the interatomic potential is based on a harmonic behavior which does not account for changes in the average interatomic separation so no thermal expansion should be observed, however, due to the natural anharmonicty of the potential surface, thermal expansion is predicted. If the thermal coefficient was plotted at each values of increasing temperature, a linear dependence would be observed.

MD

Simulating the thermal expansion of the MgO crystal using molecular dynamics, under the NPT ensemble, employs classical mechanics as opposed to quantum mechanics in the case of the QHA. Due to the nature of this calculation, a primitive cell is no longer representative of the whole material as it would indicate every cell moving in phase, which has no physical meaning in the realms of MD. A supercell containing 32 MgO units is used instead, in order to allow a representative depiction of the physical vibrations occurring in the system.

In order to compare the results of the MD calculation with that of the QHA, the primitive cell volume of the QHA was multiplied by 32.

According to MD, thermal expansion proceeds in a linear fashion with temperature, compared to the parabolic form the QHA takes. Plotting the volumes up to 2500 K highlights this difference clearly, indicating the progressive linearity and parabolic nature, as opposed to a quasi-convergence at 1000 K.

At 0 and 10 K, the system was unable to compute any values for the system. This is due to the classical approach of this model, the system does not have enough thermal energy to be distributed across the system leading to vibrational motion, unlike the quantum approach of the QHA which attributes a zero point energy to the system, arising from the Heisenberg uncertainty principle.

Conclusion

From this experiment, we can conclude that the Quasi-Harmonic approximation is a better model for the thermal expansion of the MgO crystal at lower temperatures as it exhibits zero-point energy, while the Molecular Dynamics model is suitable at higher temperatures where is it able to give a macroscopic representation of what naturally occurs. Close to the melting temperature, both models would break down as the QHA doesn’t account for bond dissociation arising from anharmonicty and a larger supercell would be required to observe the long range disorder within the crystal structure as it undergoes the transition from a solid to liquid, under the MD simulation; nevertheless, this would not be attributed to a phase transition behavior, as the system is under a rigid-ion model with no concept of 'bonds', instead it would simply be regarded as a very high energy vibration mode attainable due to the amount of energy present in the system, but this does not represent reality.

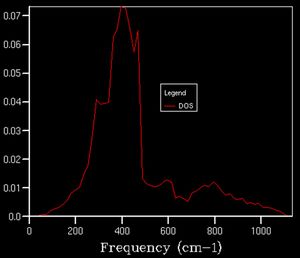
An observation made while computing the thermal expansion under QHA was the effect of increasing temperature on the structure of the DOS plot as a slight shift to lower frequencies. This proceeding is one requiring further investigation, given that the DOS is supposedly independent of temperature.

18x18x18 at 1000 K
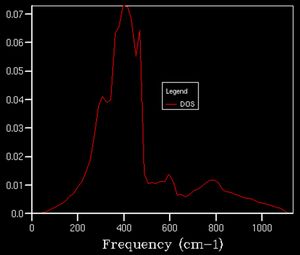
18x18x18 at 1500 K
18x18x18 at 2500 K

Bibliography

J. R. Smyth, S. D. Jacobsen. Comparative Crystal Chemistry of Dense Oxide Minerals. Reviews in Mineralogy, 40. 9. Available from: http://ruby.colorado.edu/~smyth/Oxides.pdf
MSE 2090: Introduction to Materials Science Chapter 19, Thermal Properties. Available from: http://people.virginia.edu/~lz2n/mse209/Chapter19.pdf
R. Hoffmann, "How Chemistry and Physics Meet in the Solid State", Angew. Chem. Int. Ed. 1987, 26, 846-878