Rep:Mod:Ekang912
In this Wiki report, I aimed to learn how to use GaussView programme to optimise a molecule, calculate reaction energies, and compute MOs. NH3, N2 and H2 were analyzed, and their optimisation summaries are atttached as log files. I chose H2O to investigate further, and its molecular orbitals were computed and their images are shown as png files below.
Ammonia, NH3
- Molecule Name: Ammonia, NH3
- Calculation Method: B3LYP
- Basis set:6-31G(d,p)
- Final energy E(RB3LYP): -56.55776873 a.u.
- RMS Gradient: 0.00000485 a.u.
- The point group of your molecule: C3v
- H-N-H bond angle:105.7412°
- H-N bond length: 1.018Å
The optimisation file of NH3 is linked here
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986278D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
- optimised N-H bond distance: 1.01798 Å
- optimised H-N-H bond angle : 105.74115°
NH3 Molecule |
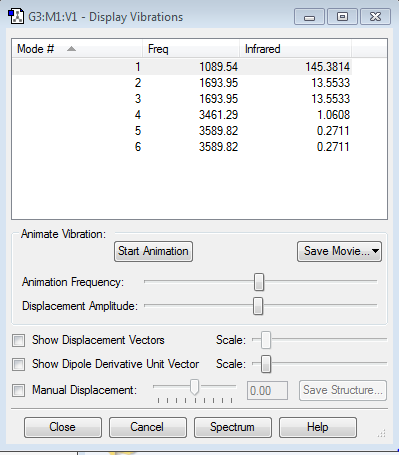
Vibration Modes
- how many modes do you expect from the 3N-6 rule?
6 modes. 3*4-6 = 6
- which modes are degenerate (ie have the same energy)?
2&3 are degenerate 5&6 are degenerate
- which modes are "bending" vibrations and which are "bond stretch" vibrations?
1, 2&3 are bending vibrations 4,5& 6 are stretching vibrations, where 4 is a symmetric stretch and 5&6 are asymmetric stretch
- which mode is highly symmetric?
4 is highly symmetric, as its point group does not change throughout the stretching motion. 1 is not highly symmetric as its point group keeps changing while bending.
- one mode is known as the "umbrella" mode, which one is this?
1 is an umbrella mode
- how many bands would you expect to see in an experimental spectrum of gaseous ammonia?
2 bands at 1089.54 cm-1, and 1693.95 cm-1. There are infrared absorptions at 3461.29 cm-1, and 3589.82 cm-1 but the transmittance is close to 0 for those vibrations. This is because, for the vibration modes 4, 5 and 6, there is not a huge change in dipole.
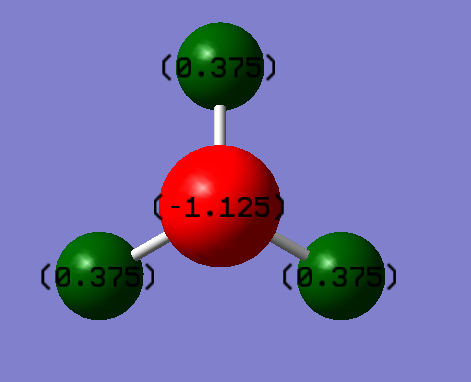
Charge Distribution
Because Nitrogen atom is more electronegative than Hydrogen atom, Nitrogen atom has a negative charge and Hydrogen atoms have positive charges. According to Pauling Scale, Nitrogen's ectronegativity is 3.04 and Hydrogen's electronegativity is 2.20
Charge on the Hydrogen atom: +0.375
Charge on the Nitrogen atom: -1.125
Nitrogen, N2
Gaussian Calculation Summary
- Molecule Name: N2
- Calculation Method: B3LYP
- Basis set:6-31G(d,p)
- Final energy E(RB3LYP): -109.52412868 a.u.
- RMS Gradient: 0.00000217 a.u.
- The point group of your molecule: D∞h
- N≡N bond angle: 180°
- N≡N bond length: 1.1055Å
The optimisation file of N2 is linked here
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000001 0.001800 YES
RMS Displacement 0.000002 0.001200 YES
Predicted change in Energy=-4.428714D-12
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Vibration Modes
1 vibration mode at 2457.34 cm-1
N2 Molecule |
Hydrogen, H2
Gaussian Calculation Summary
- Molecule Name: Hydrogen, H2
- Calculation Method: B3LYP
- Basis set:6-31G(d,p)
- Final energy E(RB3LYP): -1.17853936 a.u.
- RMS Gradient: 0.00000017 a.u.
- The point group of your molecule: D∞h
- H-H bond angle: 180°
- H-H bond length: 0.7428Å
The optimisation file of H2 is linked here
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Vibration Modes
1 vibrational mode at 4465.68 cm-1
H2 Molecule |
Reaction energy of Haber process
- (NH3)= -56.55776873 a.u.
- 2*E(NH3)= -113.11553746 a.u.
- E(N2)= -109.52412868 a.u.
- E(H2)= -1.17853936 a.u.
- 3*E(H2)= -3.53561808 a.u.
- ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 a.u. = -146.4784828 kJ mol-1
My own choice of small molecule 1: Water, H2O
Gaussian Calculation Summary
- Molecule Name: Water, H2O
- Calculation Method: B3LYP
- Basis set:6-31G(d,p)
- Final energy E(RB3LYP): -76.419737 a.u.
- RMS Gradient: 0.00006276 a.u.
- The point group of your molecule: C2V
- H-O-H bond angle: 103.7454 °
- H-O bond length: 0.9652 Å
The optimisation file of H2O is linked here
Item Value Threshold Converged?
Maximum Force 0.000099 0.000450 YES
RMS Force 0.000081 0.000300 YES
Maximum Displacement 0.000128 0.001800 YES
RMS Displacement 0.000120 0.001200 YES
Predicted change in Energy=-1.939669D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.9652 -DE/DX = 0.0001 !
! R2 R(1,3) 0.9652 -DE/DX = 0.0001 !
! A1 A(2,1,3) 103.7454 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
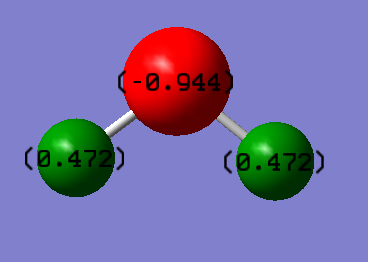
Charge Analysis
Oxygen has a negative charge since it is more electronegative. Pauling scale says that oxygen's electronegativity is 3.44 and hydrogen's electronegativity is 2.20.
- Charge on hydrogen atom: +0.472
- Charge on oxygen atom: -0.944
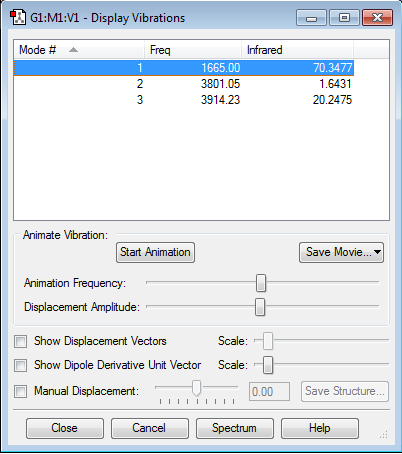
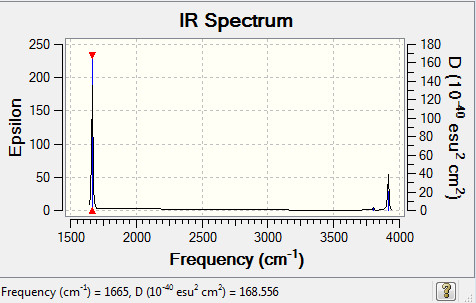
Frequency Analysis
Vibration Mode
- how many modes do you expect from the 3N-6 rule?
3 modes
- which modes are "bending" vibrations and which are "bond stretch" vibrations?
1 is bending vibration 2&3 are stretching vibrations, where 2 is a symmetric stretch and 3 is an asymmetric stretch
IR Spectrum:
My own choice of small molecule 2: Methane, CH4
Gaussian Calculation Summary
- Molecule Name: Methane, CH4
- Calculation Method: B3LYP
- Basis set:6-31G(d,p)
- Final energy E(RB3LYP): -40.52401404 a.u.
- RMS Gradient: 0.00003263 a.u.
- The point group of your molecule: TD
- H-C-H bond angle: 109.47122 °
- H-C bond length: 1.09197 Å
The optimisation file of CH4 is linked here
Item Value Threshold Converged?
Maximum Force 0.000063 0.000450 YES
RMS Force 0.000034 0.000300 YES
Maximum Displacement 0.000179 0.001800 YES
RMS Displacement 0.000095 0.001200 YES
Predicted change in Energy=-2.256043D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.092 -DE/DX = -0.0001 !
! R2 R(1,3) 1.092 -DE/DX = -0.0001 !
! R3 R(1,4) 1.092 -DE/DX = -0.0001 !
! R4 R(1,5) 1.092 -DE/DX = -0.0001 !
! A1 A(2,1,3) 109.4712 -DE/DX = 0.0 !
! A2 A(2,1,4) 109.4712 -DE/DX = 0.0 !
! A3 A(2,1,5) 109.4712 -DE/DX = 0.0 !
! A4 A(3,1,4) 109.4712 -DE/DX = 0.0 !
! A5 A(3,1,5) 109.4712 -DE/DX = 0.0 !
! A6 A(4,1,5) 109.4712 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -120.0 -DE/DX = 0.0 !
! D2 D(2,1,5,3) 120.0 -DE/DX = 0.0 !
! D3 D(2,1,5,4) -120.0 -DE/DX = 0.0 !
! D4 D(3,1,5,4) 120.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
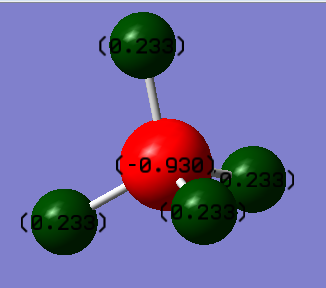
Charge Analysis
- Charge on Carbon atom: -0.930
- Charge on Hydrogen atom: +0.233
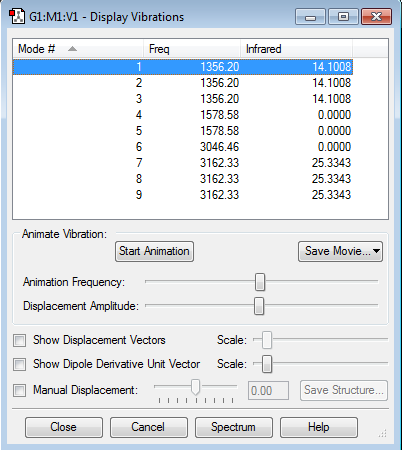
Frequency Analysis
Vibration Mode
- how many modes do you expect from the 3N-6 rule?
9 modes
- which modes are degenerate (ie have the same energy)?
1,2&3 are degenerate 4&5 are degenerate 7,8&9 are degenerate
- which modes are "bending" vibrations and which are "bond stretch" vibrations?
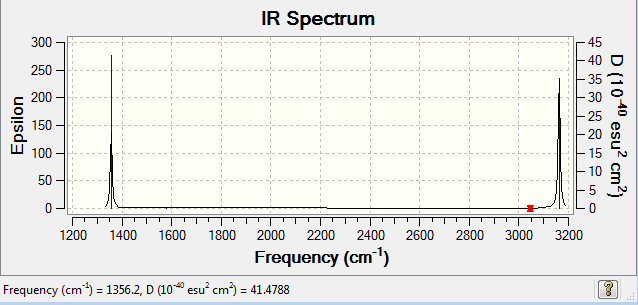
1 to 5 are bending vibrations 6 to 9 are stretching vibrations, where 6 is a symmetric stretch and 7,8& 9 are asymmetric stretch
IR Spectrum:
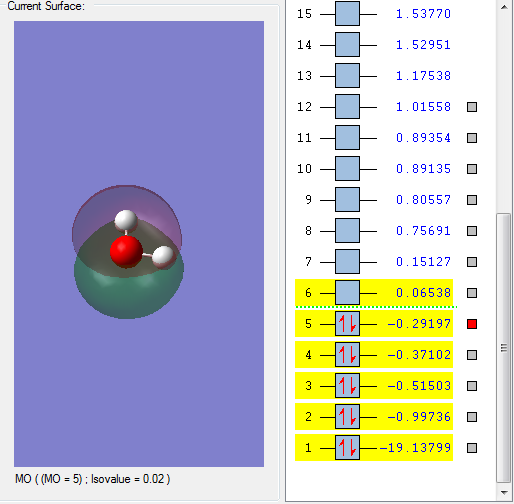
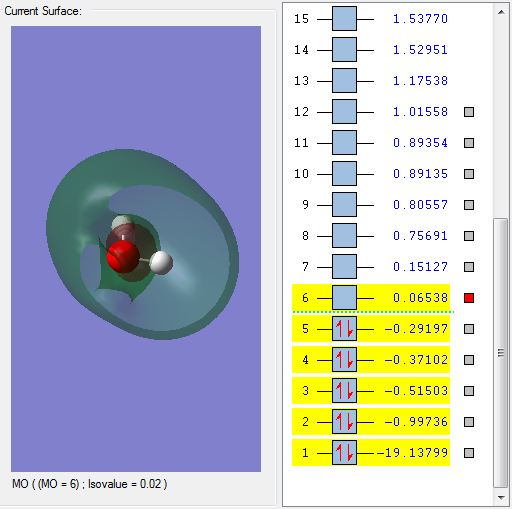
Molecular Orbitals of H2O
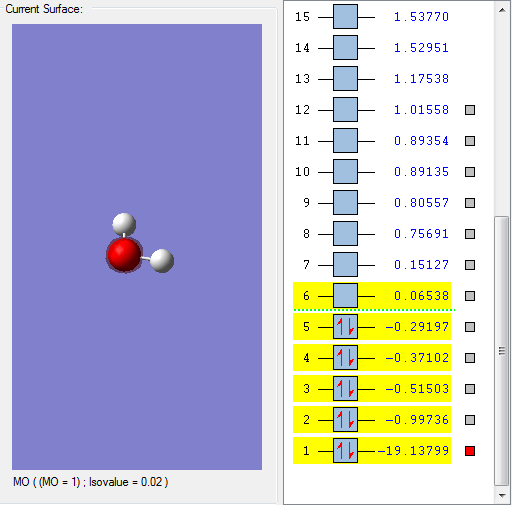
This molecular orbital is assigned to be 1a1. This is the oxygen's 1s AO. However, this molecular orbital is not so important in terms of reactivity, and it is not generally shown in the MO diagram because it has such a low energy.
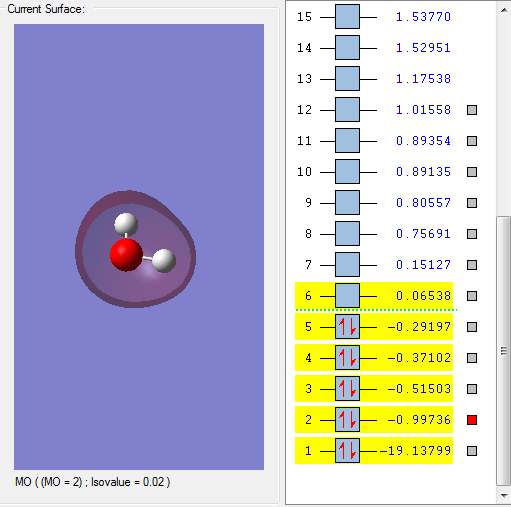
This molecular orbital is assigned to be 2a1.
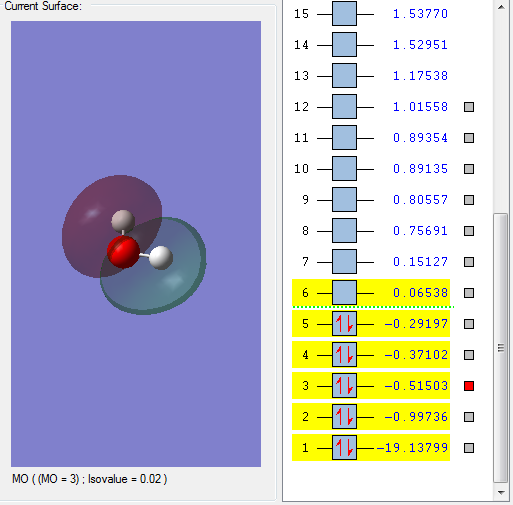
This molecular orbital is assigned to be 1b1. Fragment orbitals are closer in energy and so the interaction between the orbitals is larger for the 1b1than the 2a1 MO.
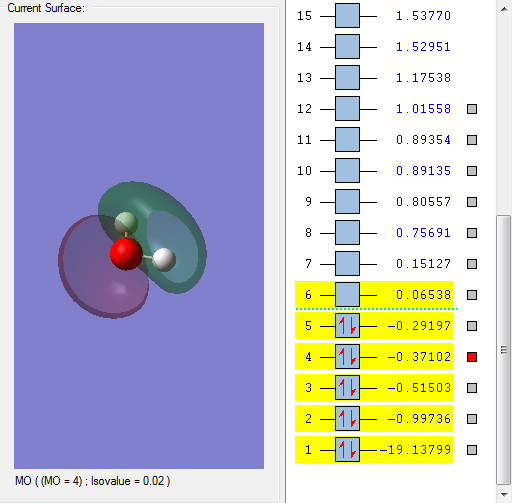
This molecular orbital is assigned to be 3a1. This molecular orbital is special because it gets mixed with 4a1 and results in net stabilization. As planar molecule 1πu and 3σg + cannot mix as they do not have the same symmetry. However, when a molecule gets geometrically distorted they become the same symmetry and mixing occurs. 1πu goes to 3a1 and 3σg + goes to 4a1. By mixing, 3a1 is stabilized.
This molecular orbital is assigned to be 1b2. b2 fragment orbital is left non- bonding as there is no other fragment orbital of this symmetry for it to interact with.
This molecular orbital is assigned to be 2b1, an anti- bonding molecular orbital. The 4a1 lies above the 2b1 MO because there is strong directional anti-bonding overlap in the 4a1 MO and weaker less directional overlap in the 2b1 MO.