Rep:Mod:Ef111

1C Part 1

The Hydrogenation of Cyclopentadiene Dimer

Scheme 1: Dimerisation of Cyclopentadiene

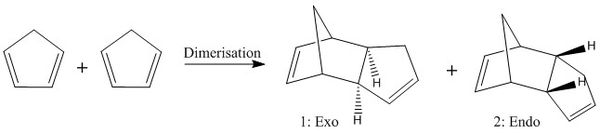
The Diels-Alder reaction is one of the most prominent pericyclic reactions within chemistry. An example of this reaction is the dimerisation of cyclopentadiene - where the diene of one molecule reacts with one of the two double bonds of the second molecule, as shown in scheme 1.

It is well known to those who have studied this reaction that the endo dimer is specifically favoured over the exo dimer. The aim for this section is to explain whether the dimerisation and the further hydrogenation of the dimer are kinetic or thermodynamic processes.

The dimerization is an example of a cycloaddition reaction where two new sigma bonds are made between the two rings. The reaction is governed by selection rules, as there are 4n+2 (where n=1) π electrons, when the reaction is subjected to heat, Huckel topology is followed, and when the reaction is subjected to light, Mobius topology is followed. This stems from the aromaticity induced within the system via the transition state, which has a strong influence on the outcome of this reaction - already indicating the possibility of kinetic control.

Both forms have been defined and optimised using Avogadro, specifically the MMFF94(s) force field, to form the lowest energy structure.

	1: Exo (kcal/mol)	2: Endo (kcal/mol)
	Dimer 1	Dimer 2
Bond Stretching Energy	3.54	3.47
Angle Bending Energy	30.77	33.19
Stretch Bending Energy	-2.04	-2.08
Torsional Energy	-2.73	-2.95
Out-of-plane Bending Energy	0.0149	0.0218
Van Der Waals Energy	12.80	12.36
Electrostatic Energy	13.01	14.18
Total Energy	55.37	58.19

The overall energy of the exo form (1) is 55.37 kcal/mol compared to the dominant endo form (2) which has energy of 58.19 kcal/mol. This strongly indicates the reaction is under kinetic control as the lower energy product is not formed. The kinetic product is the fastest formed, where the transition state energy is lower, making the product more accessible, compared to the thermodynamic product which has overall lower energy.

When considering the proximity of the two hydrogen atoms to the bridging methyl groups it would be expected this would cause considerable steric hindrance, and result in a much higher energy conformer. However, the Van Der Waals energy of both conformers are relatively similar - showing that the distance between these atoms exceeds their Van Der Waals radius. The most significant difference in energy between the isomers comes from the angle bending energy contribution. This implies that the downward bending of the cyclopentene ring is a higher energy form.

The Endo product is expected in these reactions due to secondary orbital overlaps, where favourable bonding interactions between the π orbitals of the two rings as they align, stabilise the Endo orientation.

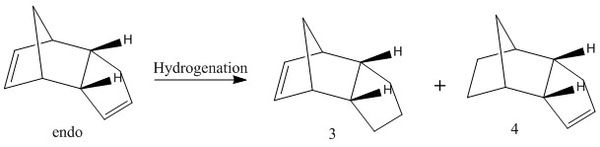
The hydrogenation reaction of the more stable dimerization product can form two possible products, the conformation of each has been optimised to give the lowest energy form using MMFF94(s). The total energy breakdown can then be analysed between the two regioisomers.

Scheme 2: Hydrogenation of Cyclopentadiene Dimer

	3 (kcal/mol)	4 (kcal/mol)
	Dimer 3	Dimer 4
Bond Stretching Energy	3.31	2.82
Angle Bending Energy	31.93	24.68
Stretch Bending Energy	-2.10	-1.66
Torsional Energy	-1.47	-0.378
Out-of-plane Bending Energy	0.0131	0.00028
Van Der Waals Energy	13.64	10.63
Electrostatic Energy	5.12	5.14
Total Energy	50.45	41.26

The total energy of 3 is 50.45 kcal/mol compared to 4 which is 41.26 kcal/mol, this is a significant difference in the energies. The considerably lower energy of molecule 4 would indicate that this would be the preferential form when the dimer is hydrogenated. This would be the thermodynamic product which should be dominant due to the energy difference. The most significant energy difference between the two forms is a result of the angle strain (difference of 7.25 kcal/mol). This can be rationalised by considering the forms of the two products. One possibilty for the difference is related to the bridgehead over the six membered ring, which causes a level of steric hinderance locked within the ring. Having a double bond in this more strained system would be less favourable as a π bond must be fairly planar for good π orbital overlap. This results in an ideal angle of 120 degrees around the sp2 carbon centres, which cannot be formed in this more strained system. Molecule 4 has hydrogenated this higher energy double bond leaving a saturated bicyclic system with more stable bond angles. The double bond within the 5 membered ring is more stable as the ring is able to distort slightly to allow for good π overlap and 120 degree sp2 angles.

Atropisomerism in an Intermediate related to the Synthesis of Taxol

Figure 1: Taxol Intermediates

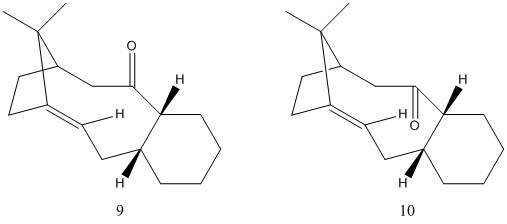
Taxol is a drug used to treat cancers, particularly ovarian. It was originally derived from the Pacific yew tree, and the multi-step synthesis required to industrially synthesise this complex molecule has a number of intermediates . One in particular, shown in figure 1, will be studied to establish the most stable conformation of the carbonyl element, either pointing up (9) or down (10).

These two molecules are examples of atropisomers, a specific type of isomer where hindered rotation around one or more single bonds causes isolated conformers to exist. These exhibit axial chirality relying on the stability of this single bond.

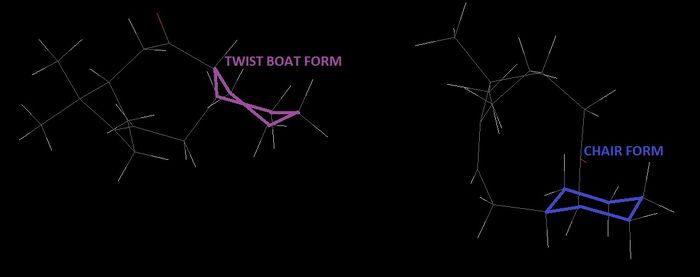
Each conformation has two different forms - one involving the cyclohexane in its chair form and one with it in the twist boat form. The energy of both of these conformers are compared to establish which is the lower energy and therefore the dominant form.

Figure 2: 9 - Chair and Twist Boats Forms

	Chair (kcal/mol)	Twist Boat (kcal/mol)
Bond Stretching Energy	7.641	7.943
Angle Bending Energy	28.27	29.499
Stretch Bending Energy	-0.08264	0.07995
Torsional Energy	0.371	2.776
Out-of-plane Bending Energy	0.995	0.970
Van Der Waals Energy	33.07	34.71
Electrostatic Energy	0.304	0.314
Total Energy	70.56	76.29

Figure 3: Cyclohexane Conformation Diagram

The chair is the more stable form of these conformers with the lower energy. Which is expected for cyclohexane when considering its energy diagram as shown in figure 3. The most significant energy difference between the two conformers resides in the torsional energy which the twist boat has much higher than for the chair, with a difference of 2.405 kcal/mol. This is a result of the nature of the twisted form, which means non-ideal bond lengths and angles are involved, compared to the chair form which has almost ideal bond lengths and angles.

The Van Der Waals energy is also different between the two forms, higher energy for the twist boat by 1.64 kcal/mol. This is a result of Van Der Waals strain between the hydrogen on C1 and the hydrogen on C4, which are pointing towards each other, this causes a certain level of repulsion which results in higher energy.

Figure 4: 10 - Chair and Twist Boats Forms

	Chair (kcal/mol)	Twist Boat (kcal/mol)
Bond Stretching Energy	7.623	7.745
Angle Bending Energy	18.96	19.19
Stretch Bending Energy	-0.1394	-0.1018
Torsional Energy	0.257	3.5157
Out-of-plane Bending Energy	0.861	0.928
Van Der Waals Energy	33.09	35.18
Electrostatic Energy	-0.04827	-0.07756
Total Energy	60.60	66.38

The chair form is also the lower energy of the two conformations for this atropisomer. With a very similar energy difference between the two forms as for atropisomer 9. The differences in energy are influenced by similar factors as mentioned above: torsional strain and Van Der Waals energy.

The table below shows the energy contributions for the lowest energy conformer of each atropisomer - both being the chair forms as rationalised above.

	9 (kcal/mol)	10 (kcal/mol)
	Taxol Intermediate 9	Taxol Intermediate 10
Bond Stretching Energy	7.641	7.62
Angle Bending Energy	28.27	18.96
Stretch Bending Energy	-0.08264	-0.139
Torsional Energy	0.371	0.257
Out-of-plane Bending Energy	0.995	0.8615
Van Der Waals Energy	33.07	33.09
Electrostatic Energy	0.304	-0.0483
Total Energy	70.56	60.60

The lowest energy atropisomer is 10, by a significant amount - this would be the thermodynamic product. The significant contributor to this difference in energy is the angle bending energy - where there is a 10 kcal/mol difference. This relates to the angle strain from the carbonyl pointing up - in the same direction as the bridging carbons and the adjacently bound hydrogen atom. This higher energy conformation is a result of the limited ability of the form to pucker, which results in a less favourable, wider angle between the adjacent carbon atoms, instead of the idealised 120 degrees.

Bridged bicyclic systems containing a double bond have in the past been understood according to Bredt's rule, developed in 1924. This stated that double bonds formed at the bridgehead tended to be less favoured. This idea was rationalised by the strain inflicted on the system by the double bond which results in distortion of the double bond away from planarity, reducing the π overlap. This rule however was developed considering small ring systems, for molecules 9 and 10 the ring being bridged contains 10 carbons. This larger ring is able to reduce the strain and maintain a reasonably planar double bond with strong π overlap. To properly consider the reactivity and therefore stabiltity of molecules 9 and 10 a more recent study must be applied.

The alkene reacts slowly for further reactions due to the nature of bridgehead olefins. To understand the reactivity of the alkene, the olefin strain energy (OS) must be considered. This is associated with the difference in energy between the lowest energy conformer of the alkene molecule and that of the hydrogenated molecule. This can be used to define stability of the bridgehead olefin.

OS is calculated for the lower energy of the two atropisomers, molecule 10, using the lowest energy conformation (the chair form). Molecule 10 has lower overall energy when compared to the lowest energy conformer of the hydrogenated version. This is somewhat unexpected, due to angle strain within the ring and bridgehead, a higher energy alkene molecule would not be surprising.

	Hydrogenated 10 (kcal/mol)	10 (kcal/mol)
Bond Stretching Energy	5.706	7.62
Angle Bending Energy	25.02	18.96
Stretch Bending Energy	0.3039	-0.139
Torsional Energy	7.435	0.257
Out-of-plane Bending Energy	0.00063	0.8615
Van Der Waals Energy	28.499	33.09
Electrostatic Energy	0.00	-0.0483
Total Energy	66.97	60.60

The energy difference and therefore the OS = - 6.37 kcal/mol. This indicates that the formed alkene is a 'hyperstable' olefin as the OS is negative and the alkene molecule is less strained compared to the hydrogenated form. Hyperstable olefins are very unreactive due to stability from the cage-like structure and the higher energy hydrogenated form. This stability is unusually not related to any steric or electronic factors which are normally dominating interactions when considering reactivity.

Spectroscopy of an intermediate related to the synthesis of Taxol

Figure 5: Molecules 17 and 18

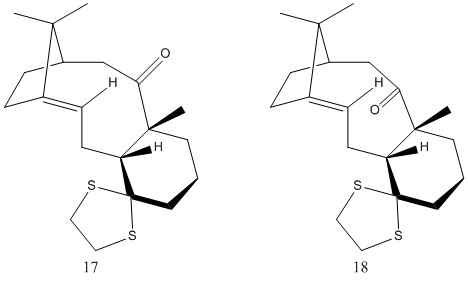
Two further atropisomeric ketone intermediates in the synthesis of Taxol will be considered in this section, molecule 17 and molecule 18 shown in figure 5. These have been energy minimised using the MMFF94s field, ensuring that the lower energy chair forms for the rings are in place when possible, before Gaussian was used to predict the NMR spectra for each compound. Molecule 18 has been particularly focused on as literature has found it to be the most stable form. The ¹HNMR and the ¹³CNMR have been compared to these literature values to establish whether they have been reasonably assigned .

The method used for the Gaussian computation was B3LYP, with the 6-31G(d,p) basis set. Additional keywords were added "SCRF(CPCM,Solvent) FREQ NMR EmpiricalDispersion=GD3" to generate NMR data and vibrational analysis. The vibrational analysis calculates a free energy for the molecule, from the entropy and a zero point energy correction. This means that the more stable isomer can be established and the difference in conformation studied.

Figure 6: Molecules 17 and 18 Lowest energy forms

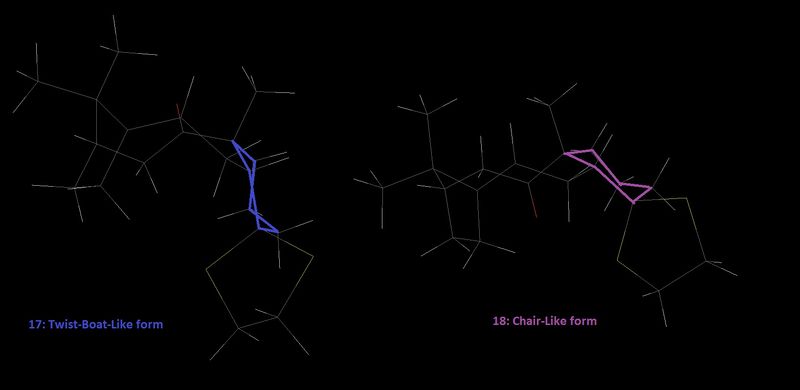
Firstly the lowest energy conformations of the two molecules will be considered. As stated by Elmore et Al. (for the analogous ring, missing a methyl) the isomer involving the carbonyl pointing up forces the conformation to be locked in a more twist boat conformation - one reason why higher energy is expected. When the carbonyl points down a more chair like structure can be formed with greater transannular interactions. This chair form is known to be more stable and therefore the molecule adopting this conformation is the more favourable form of the two atropisomers. The respective structures are shown in figure 6, where the specific conformation is highlighted for reference.

Energy Analysis

	17 (kcal/mol)	18 (kcal/mol)
	17	18
Bond Stretching Energy	15.95	15.01
Angle Bending Energy	31.406	31.00
Stretch Bending Energy	0.3877	0.6529
Torsional Energy	13.62	9.677
Out-of-plane Bending Energy	1.164	0.8688
Van Der Waals Energy	53.56	49.33
Electrostatic Energy	-7.172	-6.045
Total Energy	108.92	100.49
Gibbs Free Energy / Jmol-1	-1651.440536	-1651.461136

The energy values generated by Avogadro are shown in the table above for the optimised lowest energy conformation for the two molecules. The most significant difference in energy between the two molecules comes from the torsional energy and the Van Der Waals. The torsional energy was expected to be greater for the twist-boat like structure in comparison to the typically favoured chair form. The Van Der Waals difference can be rationalised by considering the position of the carbonyl in relation to the vicinal methyl group. For molecule 17 they are pointing in the same direction and therefore most likely overlap there Van Der Waals radii, causing a level of repulsion which causes higher energy interaction. Molecule 18 has lower energy Van Der Waals interaction relating to the increased distance between the methyl and carbonyl centres.

The Gibbs free energy values calculated by Gaussian, shown above for the two molecules are relatively similar, with only a difference of ca. 0.02 J/mol. However due to the more negative free energy for molecule 18, this will be the more stable/favourable form. This is confirmed by literature, which states that 18 is lower in energy by 4.3 kcal/mol. The value from this computation is much lower than this, potentially due to differences in the energy minimised conformations, as well as different methods and basis sets of the computations.

The lower energy observed for 18 explains why molecule 18 is preferred over molecule 17 when the interconversion energy barrier is overcome.

NMR Analysis: Chair Form

Figure 7: 1HNMR - 18

Figure 8: 13CNMR - 18

Above are the predicted NMR spectra for the chair form of molecule 18 with deuterated benzene as solvent, and TMS as a reference. Below the values are tabulated against literature values to give a reasonably clear comparison.

Computational 1HNMR		Experimental 1HNMR		Computational 13CNMR		Experimental 13CNMR
Chemical Shift (ppm)	Integration	Chemical Shift (ppm)	Integration	Chemical Shift (ppm)	Integration	Chemical Shift (ppm)	Integration
5.95	1	5.21	1	211.06	-	211.49	-
3.17	2	3.00 - 2.70	6	147.93	-	148.72	-
3.02	1			120.03	-	120.90	-
2.91	1			93.63	-	74.61	-
2.79	3			60.46	-	60.53	-
2.67	1	2.70 - 2.35	4	54.77	-	51.30	-
2.58	1			53.94	-	50.94	-
2.49	1			49.54	-	45.53	-
2.40	1			49.15	-	43.28	-
2.32	1	2.20 - 1.70	6	46.67	-	40.82	-
1.99	3			41.90	-	38.73	-
1.82	1			41.73	-	36.78	-
1.57	2	1.58	1	38.53	-	35.47	-
1.38	3	1.50 - 1.20	3	34.05	-	30.84	-
1.23	2	1.10	3	33.61	-	30.00	-
1.26	3	1.07	3	28.09	-	25.56	-
1.04	3	1.03	3	26.45	-	25.35	-
				24.40	-	22.21	-
				22.62	-	21.39	-
				21.57	-	19.83	-

The ¹HNMR computed values for the molecule of 18 vary considerably when compared to the literature values. Particularly the most deshielded hydrogen atom (connected to the sp2 carbon centre), which was experimentally found to be 5.21 ppm compared to the computed 5.95 ppm. It is difficult to directly compare the data as the experimental ¹HNMR has not been carefully separated into chemical shifts for each environment - there is a lot of grouping.

Hydrogen atoms are highly sensitive to environment, which results in ¹HNMR being very difficult to accurately compute. One of the reasons for this sensitivity is due to the high gyromagnetic ratio of hydrogen (42.578), particularly in relation to that of carbon-13 (10.708). This essentially means there is a higher probability of error with ¹HNMR than for ¹³CNMR, a fact demonstrated by these results.

One significant reason for the differences in the two sets of data is the time averaged nature of experimental ¹HNMR which is not taken into account in the computational study. This is confirmed by the significant differences in shifts between the three methyl protons which would experimentally be found to be equivalent through rapid bond rotation. This has been taken into account through averaging in the data reported above. Another potential issue is a result of an incorrect minimum energy conformation, which could be the case for this computation. It would be very difficult to know exactly if the literature conformation is the boat or the chair form and the NMR values recorded may be for the different form.

The ¹³CNMR computed values for the molecule of 18 compare much more favourably to the literature values. The top three highest shift carbon atoms are within 1 ppm of the experimental results - which does indicate the conformation used is at least similar to the actual molecular conformation.¹³CNMR are generally very useful for computational studies. This is due to a number of reasons: the carbon chemical shifts are greatly spread over a wide range (considerably more than ¹HNMR), also the data generated is less sensitive to solvent shifts, but sensitive to steric and electronic factors.

The most significantly different carbon shift value is for the carbon attached to the two sulfur atoms - which was computed at 93.63 ppm corresponding to a 74.61 ppm experimental value. A potential reason for this significant difference is the heavy atom effect. Heavy atoms, such as sulfur, have a high level of spin-orbit coupling, this is thought to cause electronic spin polarisation which interacts with the systems nuclear magnetic moments. This is considered to be responsible for a decrease in chemical shift of the nucleus bound to the heavy atom substituent. The computation does not take this into account and therefore gives a chemical shift significantly higher than expected. To improve the calculation additional pseudo potentials could be used to take into account the extra electrons of the heavy atom and correct for this factor to some extent.

NMR Analysis: Twist-Boat Form

For comparison the higher energy conformer of molecule 18, the twist boat form was also computed to give its corresponding NMR shifts shown in the table below.

Figure 9: Twist Boat 1HNMR - 18

Figure 10: Twist Boat 13CNMR - 18

Computational 1HNMR		Experimental 1HNMR		Computational 13CNMR		Experimental 13CNMR
Chemical Shift (ppm)	Integration	Chemical Shift (ppm)	Integration	Chemical Shift (ppm)	Integration	Chemical Shift (ppm)	Integration
5.27	1	5.21	1	210.58	-	211.49	-
3.29	1	3.00 - 2.70	6	148.34	-	148.72	-
3.19	1			118.91	-	120.90	-
3.06	2			88.71	-	74.61	-
2.85	2			67.85	-	60.53	-
2.52	1	2.70 - 2.35	4	55.87	-	51.30	-
2.45	1			55.46	-	50.94	-
2.35	1			49.94	-	45.53	-
2.28	2			48.00	-	43.28	-
2.14	1	2.20 - 1.70	6	44.04	-	40.82	-
1.94	2			41.97	-	38.73	-
1.82	2			37.35	-	36.78	-
1.68	1			35.19	-	35.47	-
1.58	1	1.58	1	30.92	-	30.84	-
1.40	1	1.50 - 1.20	3	28.87	-	30.00	-
1.35	3			28.59	-	25.56	-
1.22	3	1.10	3	25.73	-	25.35	-
1.15	3	1.07	3	25.16	-	22.21	-
1.04	1	1.03	3	23.39	-	21.39	-
				20.98	-	19.83	-

The Gibbs free energy of this conformer is - 1651.4595 J/mol, which is higher energy than the more stable chair conformation. When considering particularly the ¹HNMR the chemical shift data and integrations are a better fit to the literature. Specifically the alkene hydrogen which is within 0.06 ppm of the literature.

Both the ¹HNMR and the ¹³CNMR computed for the twist boat form have a stronger correlation to the literature indicating the possibility of the formed product in their reaction being not the lowest energy conformer as they thought, but the higher energy twist boat structure. This could be confirmed through a higher resolution NMR study as individually classified peaks would be required rather than grouped peaks as in this paper, to conclusively confirm this conformer.

Reactivity of molecules 17 and 18

The close proximity of the carbonyl carbon to the alkene monosubstituted carbon has a great effect of the reactivity of the molecules, particularly to transannular reactions. The optimised structures are studied using Gaussian and the distance between these two centres has been tabulated below with literature values .

	Chair Form 17	Chair Form 18	Twist Boat 18
Computed transannular olefin carbonyl distance (A)	3.025	2.998	3.351
Experimental transannular olefin carbonyl distance (A)	2.674	3.032	---

The differences between the two sets of results are interesting. Firstly the computed values of the chair forms are very similar to each other compared to the experimental values which have a noticeable difference of 0.358 A. The distinct differences indicate that the structures of the minimised forms in the literature and in this computation are not identical (although visually are very similar). Interestingly when the distance for the twist boat is considered instead of the lower energy chair form the difference between the data is very similar to experimental, 0.326 A. Molecule 17 has shorter distance than the twist boat form of 18 as in the literature. This is another potential indication of confusion between twist boat and chair forms of molecule 18 in the literature.

Both atropisomers have close enough distances between these two centre to allow for strong transannular interactions. Illustrated in this paper through reactions with OsO4.

1C Part 2

Catalyst Study

Scheme 3: Shi catalyst scheme

Scheme 4: Jacobsen catalyst scheme

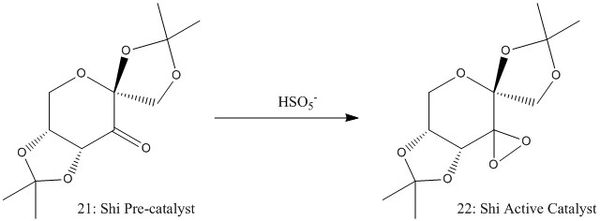
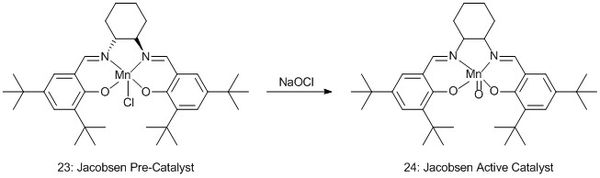
The asymmetric epoxidation of alkenes is a very useful tool in stereoselectively producing new chiral centres. Two different asymmetric catalysts will be considered here: Jacobsen, and the Shi catalyst.

Both of these catalysts have a stable pre-catalyst which reacts in situ to form the active catalyst, structures of the active catalysts 22 and 24 are shown in schemes 3 and 4.

The results of the epoxidation reactions of these catalysts on two alkenes: styrene, and 1,2-dihydronaphthalene will be studied. The general aim will be to predict and rationalise the configuration of the asymmetric epoxide formed, through use of computational modelling, NMR predictions, absolute configuration, and the active site interactions.

Generally the Shi catalyst is used for the epoxidation of trans-alkenes whereas Jacobsen catalyst is better for cis-alkenes.

Shi Catalyst Analysis

Figure 11: Shi catalyst bond lengths

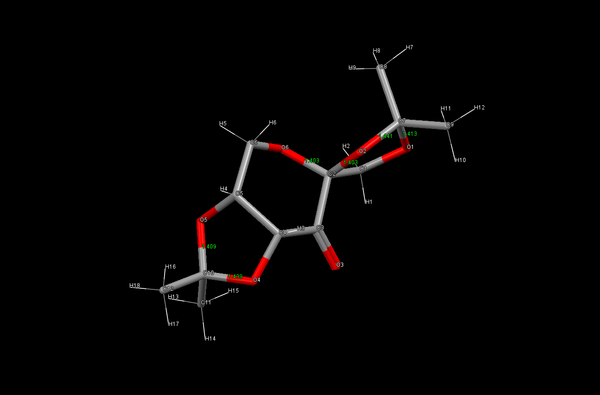
The Cambridge Crystal Database (CCDC) was searched through Conquest to find structure data for the pre-catalyst in Shi's epoxidation catalyst. The resulting structure was analysed using Mercury to give the bond lengths of the C-O bonds at each of the three anomeric centres as shown in figure 11.

Bond	Bond Length (A)
O1 -> C7	1.413
C7 -> O2	1.441
O6 -> C2	1.403
C2 -> O2	1.403
O5 -> C10	1.409
C10 -> O4	1.439

A typical C-O bond length for an ether is 1.42 A, which is midway between a number of these results for the C-O bond length of a ketal. The presence of the oxane and the carbonyl of the ring cause inductive effects to surrounding bonds. This withdrawal of electron density towards the electronegative oxygen atoms causes the differences in bond lengths as shown in the table above. The bond between O2 and C7 is closer to the oxane than O1 to C7, this causes a lengthening in this bond length as reduced electron density weakens the bond. The further away bond between O1 and C7 is shorter, as has greater electron density within the stronger bond.

Similar logic can be applied to the bonds within the O5-C10-O4 acetal group. The longer bond length corresponds to the bond closest to the electron withdrawing ketone group, which inductively weakens this bond. There is not a significant difference in the bond lengths of the two weakened bonds, just 0.002 A. Therefore the electron withdrawing nature of the oxane and the ketone can be considered to be very similar.

Figure 12: Shi Chair form

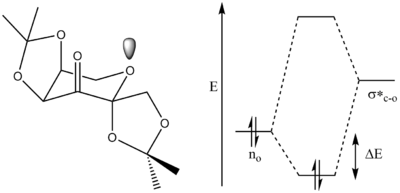
The conformation of the central 6 membered ring is a chair form, expected for a low energy, stable conformation. The conformation is slightly distorted due to the presence of the carbonyl on the ring. This sp2 hybridised carbon causes this distortion as the ideal angle of 120 degrees about this centre is not possible for this ring form. The structure of this catalyst is hugely important to selectively produce a single enantiomer. The two ketal groups are very importantly placed allowing them to act as chiral control elements as well as activating groups due to the oxygen electron density. The ketal groups are orientated so that they block one side on both sides of the catalyst face, which only allows the olefin to approach in a certain way. It has been found that the groups attached to the ketals are highly important for selectivity and reactivity - both parameters are better for smaller groups.

The bond lengths of the anomeric centre between the oxane of the ring and the ketal substituent are considerably shorter than the other anomeric centres. This is due to the strong anomeric effect, between the centres n_o -> σ*_c-o as shown in figure 12. Due to these substiuents being in the 6 membered ring the anti-periplanar positioning of them is locked - resulting in maximum anomeric effect and stronger bonds. This anomeric effect is a strongly stabilising interaction which overall strengthens the conformation, reducing the significance of higher energy axial ring components.

The long bond length of C10 -> O4 can be rationalised by the consideration of short contact interactions in the crystal structure. This distance is less than the sum of the Van Der Waals radii and therefore is not highly attractive. The presence of this interaction however signifies the spread of electron density from the oxygen lone pair, reducing the electron density present in this bond - which overall increases the bond order and lengthens the bond.

The two five membered ketal systems are in the puckered conformation: significantly lower energy than the planar form, due to the reduced steric interactions and lowered torsional strain between the substituents. Another interesting aspect to the conformation can be considered by looking at the Newman projection down the bonds. The 1.439A bond has a typically unfavourable eclipsed conformation, compared to the staggered form of the other anomeric bonds. This could also be a contributing factor to the weakened, long bond as the eclipsed form suffers from greater torsional strain making the bond higher energy.

Jacobsen Catalyst Analysis

Figure 13: Jacobsen catalyst distances

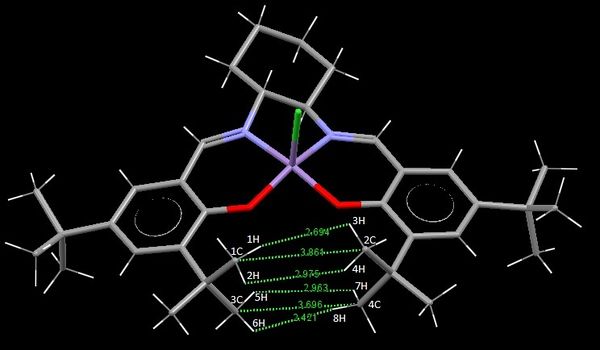
The CCDC has been searched to find a crystal structure of the Jacobsen pre-catalyst. The ring structure around the manganese centre is relatively planar, the chlorine atom protrudes from one face with the bottom face free of ligands. This has been studied and the distances between the tert-butyl groups noted as a point of interest. These two butyl groups approach very closely - unusually so for such bulky groups.

Bond	Bond Length (A)
1H -> 3H	2.694
2H -> 4H	2.975
1C -> 2C	3.861
5H -> 7H	2.963
6H -> 8H	2.421
3C -> 4C	3.696

The Van Der Waals radius for: a hydrogen atom is 1.2 A (when H.....H interaction), a carbon atom is 1.60 A . Van Der Waals, or dispersion forces, operate at greater atomic distances than bond lengths. The distance between atoms relative to the Van Der Waals radius of an atom can be attractive (favourable) or repulsive (unfavourable). The maximum attractive dispersion force between two atoms corresponds to the sum of the two atoms Van Der Waals radius. If the distance is less than this length there will be repulsion between the groups, and if it is higher there will be reduced attraction.

The distances between all of the hydrogen atoms are greater than 2.4 A (sum of Van Der Waals radii), meaning that the dispersion forces between these atoms are attractive, and stabilise the conformation by lowering its energy. 6H -> 8H distance of 2.421 A is the most attractive as it very close to 2.4 A and therefore is strongly attractive. As the distance increase the attraction decrease until there is no interaction at all. The longer distances between these hydrogen atoms are still significant in terms of attractive force as they are only 0.7 A greater than the Van Der Waals, but considerably less than the 2.4 and 2.6 A forces. This can also be applied to the carbon distances which are ca. 0.5 A greater than the Van Der Waals radii sum, and therefore mildly attractive.

The short contacts within the crystal structure of this molecule show the intense effect of the steric bulk of the four tert-butyl groups. They essentially block any significant contacts around the Manganese centre leaving it relatively open. This effect is highly important when considering the selectivity of this catalyst, the orientation of the olefin when approaching the manganese centre is pivotal for formation of a single enantiomer, these large groups block a number of potential trajectories increasing this selectivity.

The conformation of this catalyst is interesting in terms of the different fused ring conformations. The cyclohexane ring takes up the more favourable chair conformation, as shown in figure 12, which pushes the rings slightly out of plane. The five membered ring is in a puckered conformation - lower energy as reduced unfavourable steric interactions. The planar conformation of this large salen ligand is greatly important to its catalytic activity, as blocks the manganese centre, only allowing facial approach. The planar structure is dominated by the aromatic groups, reinforcing there significance.

Epoxide NMR

R-Styrene Oxide

Figure 14: R-Styrene-Oxide

Displayed here are the computed results for the 13-carbon and hydrogen NMR data for the styrene oxide (energy minimised using Avogadro). This is in chloroform with TMS standard to allow direct literature comparison. The literature data is tabulated also to allow easy visual confirmation of the generate structure. Follow links for HNMR and CNMR.

The data calculated is in good agreement with literature results, confirming the structure of the computer generated epoxides. The ¹HNMR is reasonably similar in chemical shift and integration with expected minor differences (rationalised in the taxol study above). The ¹³CNMR is also in agreement, particularly at the low shifts and the highest shift.

Computational 1HNMR		Experimental 1HNMR		Computational 13CNMR		Experimental 13CNMR
Chemical Shift (ppm)	Integration	Chemical Shift (ppm)	Integration	Chemical Shift (ppm)	Integration	Chemical Shift (ppm)	Integration
7.49	4	7.34-7.27	5	135.13	-	137.6	-
7.30	1			124.13	-	128.5	2C
3.66	1	3.84	1	123.41	-
3.12	1	3.13	1	122.96	2C	128.1	-
2.54	1	2.81	1	118.27	-	125.5	2C
				54.06	-	52.4	-
				53.47	-	51.2	-

(1R,2S)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene

Figure 15:(1R,2S)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene

The computed NMR data for (1R,2S)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene is displayed in the table below. The literature values for the HNMR are compared as well as literature values for the CNMR. Follow links for HNMR and CNMR.

This data shows a close match to the literature for both NMR, the slight expected variation is not particularly high for either, confirming the computed structures for this epoxide. Both enantiomers will have very similar NMR results and therefore have not been included.

Computational 1HNMR		Experimental 1HNMR		Computational 13CNMR		Experimental 13CNMR
Chemical Shift (ppm)	Integration	Chemical Shift (ppm)	Integration	Chemical Shift (ppm)	Integration	Chemical Shift (ppm)	Integration
7.49	1	7.39	1	133.84	-	135.6	-
7.39	2	7.28 - 7.18	2	130.38	-	131.5	-
7.19	1	7.08	1	125.55	-	128.5	-
3.59	2	3.84	1	123.83	-	127.4	-
2.88	1	3.73	1	123.42	-	127.3	-
2.27	1	2.89 - 2.71	1	121.44	-	125.1	-
2.22	1	2.54	1	56.43	-	54.1	-
1.56	1	2.41	1	54.83	-	51.7	-
		1.76	1	28.04	-	23.4	-
				24.94	-	20.8	-

Absolute Configuration of Epoxides

Optical Rotation

R-Styrene-oxide	S-Styrene-oxide
R-Styrene	S-Styrene

The two possible isomers of styrene-oxide are shown above. These can be classified through their calculated optical rotations. This has been done using Gaussian using the Cambridge variation on the B3LYP density functional method, added through keywords: "# CAM-B3LYP/6-311++g(2df,p) polar(optrot) scrf(cpcm,solvent=chloroform) CPHF=RdFreq". This gives a good prediction of the optical properties of a chiral compound which can be compared to literature calculations.

R-Styrene optical rotation:

[ALPHA] ( 5890.0 A) = -30.41 degrees
[ALPHA] ( 3650.0 A) = -94.98 degrees

The optical rotation values compare favourably to literature values, - 33.3 degrees for 589 A. Optical rotation is very sensitive to conformation and a computational value within 4 degrees shows a reasonable conformation.

S-Styrene optical rotation:

[ALPHA] ( 5890.0 A) = + 30.45 degrees
[ALPHA] ( 3650.0 A) = + 95.09 degrees

It is expected for opposite enantiomers to have the same magnitude of optical rotation but with the opposite sign, as they are computed with 100% ee. This is the case for styrene, to 0.1 degrees and validates the integrity of the calculation.

(1S,2R)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene	(1R,2S)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene
srnap	rsnap

(1R,2S)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene Optical Rotation:

[ALPHA] ( 5890.0 A) = + 155.82 degrees
[ALPHA] ( 3650.0 A) = + 522.16 degrees

The two possible isomers for 1,2-epoxy-1,2,3,4-tetrahydronaphthalene are shown in the table above. Optical rotations are calculated for one enantiomeric form as above. The styrene calculations above showed both enantiomers have reasonably equal and opposite optical rotation. Literature gives similar values of -144.9 degrees for 1S,2R as expected for these enantiomers.

Figure 16: ECD for Styrene enantiomers

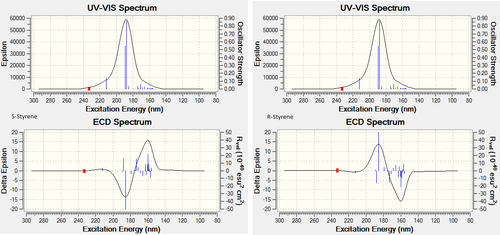
Electronic Circular Dichroism

Electronic circular dichroism has been computed for the styrene enantiomers using Gaussian The method used was CAM-B3LYP with the 6-311+G(d,p) basis set. The keywords "td(NStates=20) scrf(cpcm,solvent=chloroform)" were invoked to generate the ECD and UV-Vis spectra. These spectra are shown in figure 16.

Although literature values are not available for electronic circular dichroism (ECD), the technique can be used in a qualitative way to check chirality of a molecule. The ECD is expected to be opposite signs for the two enantiomers - shown in the graph for the two styrene enantiomers. The UV-Vis spectra are identical - expected for chiral molecules.

ECD is a useful technique to provide 3D structural information on a chiral molecule, it is highly sensitive to absolute configuration. Although the technique can be used to work out molecular structure, it requires complex algorithms which can be difficult to interpret.

Vibrational circular dichroism in this case gives the same results as ECD for this epoxide therefore the calculation was not repeated. However typically they are different, ECD relates to the electronic transitions, and VCD relates to all 3N - 6 vibrational modes. This normally results in VCD being the better technique - providing a greater level of information on the molecular structure.

Transition State Properties

Transition state modelling can be use to determine enantioselectivity through the study of computed free energies of all possible transition states. When substituents have no rotational symmetry there are 8 possible transition state forms for an alkene with the Shi catalyst, 4 for each resulting epoxide enantiomer.

The major structure of the transition state for the Shi epoxidation is either spiro or planar, depending on the position of the olefin to the dioxirane, as shown in figure 17, there are 8 forms of the alkene transition state. For the Jacobsen epoxidation there are only 4 forms for an alkene transition state, depending on the approach of the alkene to the Mn-oxo centre.

To work out the enantiomeric excess of each transition state, the computational result for the Gibbs free energy must be used, to work out K - the ratio of enantiomers resulting from the energy difference between the two potential transition states. This can then be applied to the equation below to work out respective ee values:

Failed to parse (syntax error): {\displaystyle ee = \frac{exp(-deltaG‡/RT) - 1 }{exp(-deltaG‡/RT) + 1}}

This theory is based on a kinetic concept, where the lower energy transition state will be favoured proportionally to the difference in energy between them. This is valid for a theoretical evaluation however when applied to experimental, many problems can arise, particularly variation in temperature as well as solvent effects. The level of computational modelling required is substantial to provide an accurate prediction of experimental results. A difference in energy of 1.8 kcal/mol between distinct transition states leads to ratios of 96:4 for products, showing just how difficult these predictions can be.

Figure 17: Shi Transition State Geometry

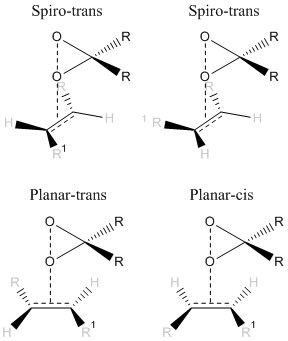
Shi Epoxidation Transition State

Styrene-oxide

Figure 18: Orbital Overlaps

The 8 possible transition state structures have all been studied, and the Gibbs free energy determined, respective values for K and ee shown here. These are calculated at -10 degrees Celsius to allow direct comparison with literature results.

R-Styrene-oxide: Lowest energy T.S	S-Styrene-oxide: Lowest energy T.S
R-Styrene	R-Styrene

Transition state 4 is the lowest energy transition state for the formation of both R and S styrene, with relatively low ee for the S form, of 26.87 %. This low ee value is a result of the low energy difference between the transition states of the two enantiomeric forms. The different enantiomeric forms are a result of the face of the alkene attacked. Forming the oxygen on the Re face produces the R-styrene, whereas the Si face forms the S-styrene enantiomer.

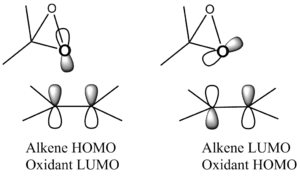
These lower energy forms can be rationalised by the study of the orientation of the two substrates to each other. It is well known that spiro transition states for the Shi catalyst with an olefin are lower energy than planar or hybrids. This can be understood by the consideration of the secondary orbital interactions shown in figure 18. There are two significant HOMO-LUMO bonding interactions between the olefin and approaching oxygen. The alkene HOMO with dioxirane LUMO: π_c-c -> σ*_o-o and alkene LUMO with dioxirane HOMO n_o -> π*_c-c. This interaction involving the oxygen lone pair is maximised when the transition state is spiro, and eliminated in the planar geometry. Figure 19, taken from literature, gives an idea of how the stereochemistry is controlled through minimising unfavourable steric interactions.

Figure 19: Stereochemistry control factors

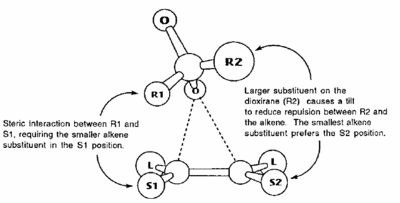
The transition states can be described as synchronous or asynchronous, referring to the equal or unequal C-O bond formation. None of the 8 potential transition states are synchronous planar - preferring to form more of a hybrid structure. Transition state 4 for both enantiomers are highly spiro, the difference in energy resulting from the level of synchronicity and the face of the alkene. The lower energy S form has a more asynchronous structure than the reasonably synchronous structure of the R form. For this highly unsymmetric alkene it is reasonable to think the asynchronous transition state would be more favourable to give higher amounts of the S enantiomer. The asynchronous form increases orbital interactions between the oxygen lone pair and the olefin π* orbital, another reason for the lower energy of this form.

The literature for this olefin states a product with R stereochemistry, and an ee of 15 %. This does not agree with the results of this transition state analysis, however the low ee value shows the R form is not favoured by a vast amount. Reasons for this difference reside in potential inaccuracies in the computation, and the very low energy difference between the two transition states. Being a monosubstituted olefin, styrene has a number of issues when it comes to epoxidations due to the lack of steric interactions on one side of the alkene.

1,2-epoxy-1,2,3,4-tetrahydronaphthalene

The 8 possible transition state structures have all been studied, and the Gibbs free energy determined, respective values for K and ee shown here. These are calculated at -10 degrees Celsius to allow direct comparison with literature results.

1R,2S-epoxy-1,2,3,4-tetrahydronaphthalene: Lowest energy T.S	1S,2R-epoxy-1,2,3,4-tetrahydronaphthalene: Lowest energy T.S
R-Styrene	R-Styrene

This transition state study has given S,R product to be the major form following the lower energy transition state, the enantiomeric excess for this is surprisingly high at almost 100 %. The specific enantiomer formed compared favourably with literature, which also predicted the S,R product, but the enantiomeric excess is significantly different - 32 %.

When considering the form of these two transition states, once again the lower energy S,R geometry has an asynchronous spiro transition state. The slightly higher energy R,S geometry is a synchronous spiro form. This confirms the idea of the more stabilising asynchronous form with better bonding orbital overlaps. Another factor to be taken into account for this alkene is steric repulsions,as shown in figure 19. The benzene ring of the alkene comes into relatively close contact with the methyl groups of the adjacent ketal for the higher energy R,S form. When the alkene is orientated on its Si face these repulsions are avoided for the S,R form, hence reducing its energy.

This indicates that the difference in energy of the transition states is not the only factor in determining which enantiomer is formed, there are a substantial number of experimental and computational factors discussed below.

Computation Analysis

Both of the Shi computational results have substantial variation with literature values for a number of reasons. Difficulties with computer models of the Shi epoxidation are well known, which can provide a reason for discrepancies between experimental and computational. Solvents effects are one significant reason for these. The transition state generated has greater hydrogen bonding which would obviously be significantly stabilised through solvent effects. Without a sophisticated continuum solvation model these effects may not be accurately portrayed, with a result of inaccurate computed enantiomeric selectivity.

Another problem for computational models arises from the many low energy transition states for the Shi epoxidation. These are conformationally distinct, and it is very difficult to be sure that the conformer analysed is the experimental conformer expected. It has also been found that the degree of conformational flexibility is relatively high for the Shi catalyst, meaning that a significant number of forms exist^[28].

Finally the results attained from the Shi epoxidation are highly dependent on the reaction conditions, literature shows a number of different methods using the same catalyst, temperature and olefin however getting a wide variety of results. The effects that go on in these reactions cannot be accurately modeled using computations, as don't consider time dependence as well as side product competition.

Interestingly, it has been noted in literature that the ΔG^‡ calculated from the transition states is systematically overestimated. This led this particular group to reduce this value by 2/3 before calculating ee. This has not been done for this study but should potentially be considered in future studies to establish more feasible ee values^[28].

Jacobsen Epoxidation Transition State

Figure 20: Jacobsen transition state geometry

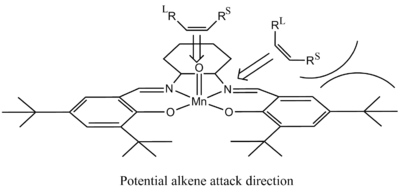
The Jacobsen catalyst is known for good selectivity with cis-alkenes. The alkenes considered here have been shown in literature to form epoxides with good selectivity and yields. The active catalytic species is the Mn^V-oxo complex, and the approach of the alkene to this centre, as shown in figure 20, can be used to understand the high enantiomeric selectivity. This approach is based on repulsive steric and electronic interactions between the alkene and salen ligand. It is generally accepted that the double bond approaches side on, as shown, with two potential angles. Approach from the di-imine bridge avoids interaction with bulky t-butyl groups, however approach over the aryl group could be favoured if π-π interactions occur. Both paths form the same enantiomeric product due to the same orientation of the large and small R groups.

Styrene-oxide

R-Styrene-oxide: Lowest energy T.S	S-Styrene-oxide: Lowest energy T.S
R-Styrene	R-Styrene

All transition states are considered for the Jacobsen epoxidation with the respective values for K and ee shown here. Both transition state possibilities for the different epoxides favour the S-styrene-oxide, as this has lower energy for both cases. The reason for this resides in the form of the lowest energy transition states, which show the side on approach to be valid (all potential transition states approach side-on). Due to the electron rich phenyl group the approach seems to be more over the aryl of the Salen ligand in these models, showing there is a level of electronic dominance over sterics.

The two transition states which follow the orientation of large to small groups as shown above are R2 and S1, which are both the lower energy of the respective R and S possibilities. Overall however the S forming transition states are both lower than corresponding R forming ones. This is potentially due to more favourable π-π stacking interactions as the S form has better overlap between the alkene phenyl ring and those of the Salen ligand. The R form still has these π interactions, but they are not as strongly stabilising as poorer overlap.

The R2 transition state following the necessary large/small orientation is considerably closer in energy to the lower energy S state than the corresponding T.S. 1 values. This results in a lower ee value, ~ 50%, for this transition state compared to 99.97 % for transition state 1. Overall due to the lower energy transition state of transition state 1, this is most likely to be the dominant reaction pathway followed, which would result in high selectivity for the S-Styrene oxide enantiomer.

Literature shows that styrene has a lower ee, 50 - 70 % compared to a number of cis-alkenes. This is thought to be due to the fact that styrene is a terminal olefin which may undergo addition with lower catalyst enantiofacial selectivity than for more substituted olefins. This relates to the transition states considered above, as the correct orientation of the olefin for the R transition state was shown to be higher energy than the opposite orientation for the S transition state, meaning that the selectivity between the orientations is lower. It is agreed that the dominant epoxide formed will be S-styrene-oxide - confirming the computational result.

1,2-epoxy-1,2,3,4-tetrahydronaphthalene

1,2-dihydronaphthalene is a cis-olefin and so already would be expected to yield higher enantiomer selectivities than styrene.

1S,2R-epoxy-1,2,3,4-tetrahydronaphthalene: Lowest energy T.S	1R,2S-epoxy-1,2,3,4-tetrahydronaphthalene: Lowest energy T.S
R-Styrene	R-Styrene

All transition states are considered for the Jacobsen epoxidation with the respective values for K and ee shown here. The S,R-epoxide is favoured by both transition states for this olefin, with higher enantiomeric selectivity: 99.99 % for transition state 1, and 83.45 % for transition state 2. These ee values are considerably stronger than for styrene, showing the greater catalytic ability of the Jacobsen catalyst for cis-olefins. This result compares favourably to the literature which states the product as S,R also with ee of 86 %, a very similar value to our transition state 2.

These transition state models can not be entirely trusted due to the lack of one of the important tert-butyl groups which should effect the orientation of the approaching olefin due to steric reasons. This reason, as well as issues mentioned above for the Shi catalyst, is responsible for discrepancies between literature and computed results.

However Jacobsen epoxides are more accurately predicted using computational models compared to Shi modelling. For both alkenes the computation gives the experimental enantiomer with reasonable ee values. The computational models of these transition states lack a tert-butyl group on the salen ligand, steric interactions with this group would be significant for this active site. Therefore a considerably more accurate study could be undertaken with this bulky group included.

Active site Interactions

The non-covalent interactions and QTAIM were both computed for the lowest energy transition state of the nap S,R-epoxide (T.S. 4 as shown in jmol above). Non-covalent interactions, such as hydrogen bonding, electrostatic, and close approaches, are weaker than covalent interactions however have a great deal of significance when applied to transition state structures.

Non-covalent Interaction

Orbital

It is difficult to fully define a hydrogen bond, whether they are specifically related to the surrounding topology or the presence of a BCP has been heavily debated in the literature. As both of the computational models studies here provide little in terms of an accurate quantitive indication of the strength of interaction, the typical assumption will be made than an interaction involving a hydrogen with an electronegative heteroatom - such as oxygen, constitutes a hydrogen bond. Whereas forces between two similar atoms are considered dispersion forces.

The NCI for this transition state is shown above. The bond forming area is shown by a multicoloured ring between the olefin and an oxygen of the dioxirane, this ring is mainly blue, signifying the strong attractive, half-covalent interaction between these two positions predicting the bond formation.

There are substantial real NCI interactions around this bond forming area between the two reacting molecules, shown by green surfaces. These are mildly attractive interactions which are very important in stabilising and lowering the energy of the transition state. The extent of these attractive interaction gives an indication of why the Shi catalyst is so effective in selectively forming a single enantiomer. Although non-covalent interactions are non-specific the strength and number of these interactions could substantially favour a single orientation over a different one. There are very few repulsive interactions in this transition state, with none residing between the two molecules, this can help to maintain the low energy of this particularly transition state.

The two sites where red, strongly repulsive forces are found are between the two ketal sites on the Shi catalyst. This is repulsive due to the high electron density of both oxygen atoms causing electronic repulsion between the like charges. The ring oxygen of the Shi catalyst is located far enough from substituents that no repulsive interactions arise, just moderately attractive favourable hydrogen bonding interactions with the hydrogen atom of the adjacent methyl group.

Figure 21: QTAIM

Electronic topology

The QTAIM generated for this same transition state is shown in figure 21. The position of the generated bond topological critical points (BCPs: yellow spheres) have been visually analysed, due to software limitations coordinated cannot be found.

There are 7 of these BCPs shown in this QTAIM. Two of these are intramolecular residing within the Shi catalyst. The remaining five are formed between the olefin centre and the Shi catalyst. The hydrogen bonding interaction between the centre of the olefin and the bottom face oxygen of the dioxirane indicates the positioning of the epoxide. This interaction clearly shows the spiro arrangement of the transition state, confirming this orientation for the lowest energy approach.

The four remaining interactions between these groups are focused on the hydrogen atoms of the olefin. Two of these are hydrogen bonding interactions with the two oxygen atoms adjacent to the ring oxygen of the Shi catalyst. The other two interactions are between closer hydrogen atoms of the Shi catalyst with the olefin hydrogen, these are weaker interactions but still provide a stabilising force for this transition state.

This model once again indicates the reasons for the high enantiomeric selectivity - five interactions at the olefin centre is a large number across the four atoms and the exact orientation of all groups in both the catalyst and the substrate is critical in maximising these interactions. The interactions can only occur on this face of the Shi catalyst due to the close orientation of the ketal groups, if these were further away these interactions would be limited at best.

New Potential Candidates

Figure 22: Pulegone epoxide

An interesting potential new candidate for future study is pulegone epoxide, structure shown in figure 22. This has a molecular weight of 168.2 making it suitable for complex computational calculations in short spaces of time. The optical rotation has been confirmed in the literature countless times to be -19.5 degrees for the R enantiomer. NMR data is readily available for comparison, as well as a circular dichroism study, which can be computed to further compare the conformation to experimental data. Due to the presence of the cyclohexane ring, the conformation can be thought of in terms of cyclohexane conformations, relating to the first part of this computational study.

The starting material for this epoxidation is pulegone, a cheap, readily available, low hazard, naturally occurring compound. It is derived from mint essential oils and has a number of interesting properties. It behaves as an insecticide and also is used in flavouring agents due to its sweet smell.