Rep:Mod:EZtransition
Transition States and Reactivity
Ekaterina Zvyagintseva
Introduction
In this experiment chemical reaction pathways were studied and analyzed by computationally predicting, modelling and optimizing different structures using various computational techniques. In particular the study focused on the Cope rearrangement of 1,5-hexadiene and Diels-Alder cycloaddition of a simple system of ethylene and butadiene. A more complex study of regioselectivity between maleic anhydride and cyclohexa-1,3-diene was also carried out.
Transition state of any reaction is an intermediate structure between the reactants and products with the highest energy on a reaction coordinate. Those structures are usually difficult to isolate and study experimentally due to their short lifetime. However those structures can provide us with crucial information with regards to reaction activation barriers and most importantly can help explain products geometric and structural properties. For this reason we focus of studying transition structures using computational methods.
GaussView program was used to compute all of the above reactions. Gaussian uses Molecular Orbital (MO) and Quantum Mechanical (QM) theories to compute the required structures. Throughout this study two different levels of theory were used to optimise our structures. First and most popular is the Hartree Fock (HF/3-21G) level of theory with 3-21G basis set. All the calculations are done by numerically solving the Schrodinger equation using matrices to find the Slater Determinant. HF sets all the electronic wavefunctions to be antisymmetric and employs approximations such as Hartree Potential (making electron movements independent of one another). The second level of theory - Density Functional Theory (DFT B3LYP/6-31G*) was used to further optimise structures at a higher level of accuracy. DFT is based on Hohenburg-Kohn therem and uses the electron density as its fundamental property. DFT calculations are more computationally demanding, but produce more accurate results, which was especially obvious when comparing the activation energies calculated using the two methods.
Nf710 (talk) 16:06, 25 February 2016 (UTC) In general HF methods are more accurate, but this case is an exception. in HF you model the current state of the molecule with a single slate determinant which is antisymetrised.
Cope Rearrangement
Cope rearrangement is classed as a concerted pericyclic type of reaction, namely a [3,3] sigmatropic shift. This reaction is a 4n+2 electron, thermally allowed reaction following Woodward-Hoffmann rules. It has been proposed and now widely accepted that the transition state structure of Cope rearrangement is either a “boat” or a “chair” like structure. In the first part of the experiment different 1,5-hexadiene conformers were analysed in order to locate a low-energy minima and hence find the transition structures of the lowest energy needed to predict the preferred reaction mechanism. Experimentally it was found that chair structure is that of the lowest energy[1] and the main focus of this part of the study was to prove this computationally.
In order to compute the transition states, reactants and products were first optimised. 1,5-hexadiene has different structural conformers due the rotational freedom of the sp3 C-C single bond which splits into two categories – antiperiplanar and synperiplanar, known as anti and gauche respectively.
An anti linkage conformer of 1,5-hexadiene was drawn and cleaned up in GaussView. This structure was then optimised using HF/3-21G level of theory. Results summary of the optimised structure was saved for future reference and the obtained structure was then symmetrised in order to find its point group. All the results are summarised in Table 1.
| Summary | Structure | Point Group | ||
|---|---|---|---|---|

|
Ci |
Comparing results with Apendix 1 it was found that anti 2 conformer was modelled.
Subsequently a gauche linkage conformer was drawn and optimised using the same level of theory in order to compare their relative energies. It was predicted that the anti-conformer would be that of the lowest energy due to a less hindered arrangement of atoms with a 180 dihedral angle of the carbon chain. Against basic chemical intuition optimised gauche conformer was found to have a more negative energy which would suggests that it is in fact a more stable conformer. Resulting structure was also symmetrised and point group was found. Results summarised in Table 2. were compared to those in Apendix 1 and it was established that produced conformer is gauche 3.
| Summary | Structure | Point Group | ||
|---|---|---|---|---|

|
C1 |
At first relative energies might appear to be anomalous, but after further analysis of HOMO and LUMO molecular orbitals it was concluded that this difference in energy might be due to secondary orbital stabilisation interactions of vinyl hydrogens with C-C double bond electron cloud and the two π clouds of C-C double bonds. Those interaction are shown in Table 3. First type of interaction mentioned appears in literature as the C-H π interaction.[2]
Nf710 (talk) 16:16, 25 February 2016 (UTC) Very nice use of the orbitals to explain the relative energy ordering
| C-C pi interactions | C-H pi interactions |
|---|---|

|

|
The anti 2 structure was then further re-optimised using the DFT B3LYP/6-31G* level of theory discussed in the Introduction. Resulting structure had correct energy and point group as before. Geometrically the two optimised structures appeared to the very similar. Bond length of C-C bonds shown in Figure 1 are summarised in Table 4. In general it can be concluded that although DFT method is more computationally accurate, geometry of the structure optimised using HF method is predicted to a high enough level.
Nf710 (talk) 16:18, 25 February 2016 (UTC) Do you have a reference to back this up?

| HF/3-21G
Bond length/A |
B3LYP/6-31G*
Bond length/A | |
|---|---|---|
| C1-C4 | 1.31610 | 1.33352 |
| C4-C6 | 1.50888 | 1.50419 |
| C6-C9 | 1.55230 | 1.54814 |
Re-optimised anti 2 structure was used for frequency analysis calculations in order to find the thermochemical data of the conformer. Frequency analysis can also confirm that the critical point obtained is in fact in a minimum. As can be seen in Figure 2 all the vibrational frequencies calculated
are real and positive which a minimum critical point. Predicted vibrational spectra for the reactant was also produced – Figure 3.


Table 5. summarises the thermochemical data calculated and extracted from the log file. The electronic and thermal energies can be further used to calculate the activation energy of the overall reaction.
| Thermochemical data | Value /Hartree |
|---|---|
| Sum of electronic and zero-point Energies | -234.469212 |
| Sum of electronic and thermal Energies | -234.461856 |
| Sum of electronic and thermal Enthalpies | -234.460912 |
| Sum of electronic and thermal Free Energies | -234.500821 |
Optimising the Chair transition structures
Chair transition structure was built and optimised using two different methods – Berny redundant coordinate method and Frozen coordinate method. Results of each were summarised and compared.
Berny method

A guess structure for the “chair” transition state was drawn using two allyl fragments optimised at the HF/3-21G theory level and positioned in an orientation approximately resembling that of a chair transition state seen in the Apendix 2. Terminal ends of the fragments were placed 2.2Å apart to produce a better model. Optimisation and Frequency analysis was carried out at HF/3-21G level including the calculation of force constants. Unlike the conformer analysis, this time structure was optimised to a transition state TS (Berny) and not the minimum.
It is expected that there will be an imaginary frequency will be found in a true transition state due to a negative force constant being produced as a result of a negative second derivative of the potential energy surface. Hence when frequency is calculated a square root of a negative force constant will result in an imaginary number. Such frequency is indeed found upon the optimisation at -817.94 cm-1 . Animation of the vibration corresponding to this frequency Figure 4 shows that expected Cope rearrangement model has been successfully made.
Frozen coordinate method
A previously made guess transition structure was used again. This time bond distance between terminal carbons on allyl fragments was set to be exactly 2.2Å and then frozen in Create New Coordinate tab. Fixing the distance in place of the proposed new bond allows the structure to be optimised separately. Frozen structure was optimised to a minimum using the HF/3-21G theory. As can be seen in Figure 5 terminal carbons in the resulting structure remained 2.2 Å apart.
Following bonds were then set to be differentiated under the Create New Coordinate tab. Newly set structure was optimised as a transition state using the same level of theory as before. Successful calculation once again produced an expected chair transition structure which can be seen in Figure 6.
Two methods of finding the transition structure were compared using the bond geometries depicted in Figure 7 . Results are summarized in Table 6.
| Berny Optimisation
Bond length/A |
Frozen Coordinate
Bond length/A | |
|---|---|---|
| C1-C6 | 1.38925 | 1.38932 |
| C6-C14 | 2.02039 | 2.02058 |
| H13-H5 | 3.10659 | 3.10637 |
| H12-H4 | 2.63183 | 2.63125 |
| H12-H5 | 2.54556 | 2.54487 |
Nf710 (talk) 16:24, 25 February 2016 (UTC) Good geom comparison
Optimising the Boat transition structure
Boat transition structure was found using QST2 method. In this method GaussView is given both the reactant and the product structures in order to find the most accurate transition state structure. In this example previously optimised anti 2 structure was used as a reactant and its mirror image with re-ordered carbon atoms as a product. Optimisation and Frequency calculation was submitted to find transition state using TS Berny Optimisation at HF/3-21G level of theory. Unfortunately calculation failed due to Gaussian not recognising the possibility of sp3 C-C bond rotation. Previous structures were modified manually to set a dihedral angle between 4 central carbons to 0° and C 2-3-4/C 4-5-6 angle to 100°. New structures are shown in Figure 8. Correct structures were then submitted for Optimisation and frequency analysis at the same level of theory. This time transition structure was found successfully and can be seen in Figure 9.(BoatOpt.mol) As previously discussed if true transition structure is found we would expect to find an imaginary frequency. In this case such frequency appeared to be -840.28cm-1, visualisation of the corresponding vibration shown in Figure 10 confirms that the correct transition structure was found.


Intrinsic Reaction Coordinate Analysis

Upon visually inspecting optimised Chair and Boat transition structures it was concluded that it is virtually impossible to predict which conformers of 1,5-hexadiene they connect. However such information would be very useful for predicting correct reaction paths. It is possible to find those structures using computational modelling. GaussView was used to carry out the Intrinsic Reaction Coordinate analysis where the minimum energy path on the PES can be followed down the slope to its local minimum in a series of steps which can be later analysed.
Previously optimised Chair transition structure was taken for the IRC analysis. The calculation converged after 44 steps at which gauche 2 conformer was found to be the conformer connecting chair transition structure (Figure 10). Graph of total energy along IRC showing that the calculation converged can be seen in Figure 11.
Nf710 (talk) 16:26, 25 February 2016 (UTC) Correct conformer found
Activation energy of Cope rearrangement
Both Chair and Boat transition structures were re-optimized at a higher level of theory (DFT B3LYP/6-31G*) and frequency analysis was carried out to find the activation energy for both reactions. The activation energy was calculated using anti 2 conformer energies as the reference. Table 7 summarizes the total energies found for each transition state. Summary of activation energies at 298.15K can be found in Table 8. It is clear from the values obtained that the B3LYP/6-31G* method produces a much more accurate calculation and hence its activation energies are much closer to the experimentally obtained ones.
| Structure | HF 3-21G | HF 3-21G | B3LYP/6-31G* | B3LYP/6-31G* |
|---|---|---|---|---|
| Electronic energy | Sum of electronic and thermal
energies at 298.15K |
Electronic energy | Sum of electronic and thermal
energies 298.15K | |
| Chair | -231.619322 | -231.461340 | -234.54309307 | -234.409009 |
| Boat | -231.602802 | -231.445296 | -234.55698303 | -234.396008 |
| Anti 2 | -231.692572 | -231.532566 | -234.61170280 | -234.461856 |
| HF 3-21G (kcal/mol) | B3LYP/6-31G* (kcal/mol) | Experimental at 0K (kcal/mol) | |
|---|---|---|---|
| ∆E (Chair) | 45.694 | 33.162 | 33.5 ± 0.5 |
| ∆E (Boat) | 54.762 | 41.320 | 44.7 ± 2.0 |
Nf710 (talk) 16:31, 25 February 2016 (UTC) I think you have worked out your energies without taking account for zero point energies. Other than that this report is good you have done everything asked of you but you havent shown a great deal of understanding in the methods.
Diels-Alder Reaction
Reactants
In this part of the experiment a simple Diels-Alder reaction of cis butadiene and ethylene was modelled and analysed. This Diels-Alder reaction is a Woodward-Hoffman thermally allowed 4s+2s electron type of pericyclic reaction. In order to analyse the reaction pathway and computationally prove that the reaction is thermally allowed a prototype transition state structure was made and optimised using AM1 semi-empirical molecular orbital method. A comparison of HOMO and LUMO molecular orbital of the reactants and their transition state must be made in order to arrive to a necessary conclusion.
First cis-butadiene and ethylene molecules were built and optimised using the method mentioned above. A summary of this optimisation can be seen in Table 9.
| Reactant | Summary | Structure | ||
|---|---|---|---|---|
| cis butadiene | 
|
|||
| ethylene | Find |
(^Placeholder Tam10 (talk) 16:55, 24 February 2016 (UTC))
HOMO and LUMO molecular orbitals were visualised and compared. As can be seen in Table 10. HOMO of cis butadiene and LUMO of ethylene was found to be anti-symmetric with respect to the plane. It would be expected that the symmetry of those molecular orbitals would match. In a classic cycloaddition reaction a HOMO of diene will interact with a LUMO of dienophile. In this case MOs shown prove that a favourable interaction between those orbital is in fact possible. A second corresponding pair of orbitals, LUMO of the butadiene and HOMO of ethylene, was found to be symmetric with respect to the plane.
| HOMO | LUMO | |
|---|---|---|
| cis butadiene | 
|

|
| ethylene | 
|

|
Simple Diels Alder Reaction
A prototype of Diels-Alder transition structure was built by using a GaussView premade bicyclo system and deleting the extra -CH2-CH2- fragment. This way it insured that the calculation will run correctly as all the angles and bond distances are set close enough to the real transition structure. The distance between the terminal carbons was set at 2.1A and the resulting structure was optimised using the same level of theory as for the reactants and the frequency analysis was carried out.
A summary of the optimised transition structure can be seen in Table 11. Presence of one imaginary frequency at -956 cm-1 (animated in the table) confirmed the formation of a true transition state.
| Summary | Structure | TS vibration | ||
|---|---|---|---|---|

|

|

Bond distances of the resulting structure were measured and compared to the typical sp3 and sp2 C-C bond lengths. Table 12 summarises the bong distances of the transition structure labeled in Figure 12.Typically a single C-C bond is approximately 1.54 Å, C-C double bond is around 1.34 Å and the typical van der Waals radius is approximately 1.7 Å. Comparing those values to the ones tabulated above it can be concluded that the C1-C2/C3-C4 and C1-C4 bonds are all intermediate between sp3 and sp2 C-C bond which would correspond to the predicted elongation of terminal end and shortening of the central C-C bond. Distance between the forming/breaking bond in the prototype structure is 2.12 Å which is approximately twice the van der Waals radius of carbon. This shows that carbons are positioned close enough to experience the attractive forces favouring the formation of two new sigma bonds. As can be seen in the animation above, the bond formation is synchronous.
(Twice VdW(C) is 3.4 Å though Tam10 (talk) 16:55, 24 February 2016 (UTC))
HOMO and LUMO molecular orbitals of the transition state can be seen in Table 13 The HOMO MO exhibits a clear resemblance with HOMO of butadiene and LUMO of ethylene combined together to form an anti-symmetric transition state. Similarly LUMO MO was found to be a combination of butadiene LUMO and ethylene HOMO resulting is an overall symmetric MO.
| Carbon number | Bond length/A |
|---|---|
| C1-C4 | 1.39750 |
| C1-C2 | 1.38192 |
| C2-12 | 2.11895 |
| C12-9 | 1.38288 |
| HOMO | LUMO |
|---|---|
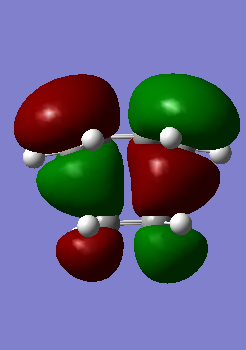
|

|
The Reaction of Maleic Anhydride and Cyclohexadiene
In the last part of the experiment a more complex version of a Diels-Alder reaction was analysed. Due to an increase in structural complexity of a dienophile maleic anhydride reaction can result in two different conformers being formed depending on the direction of anhydride approach at the cyclohexadiene face. The two posisble products are Endo and Exo. Depending on relative energies the two transition state product formed will either be a kinetic product with lover TS energy or the thermodynamic one with higher TS energy. Finding out which product is the most stable and why was the main purpose of this part of the study.
Due to a more complex geometry of the reaction, transition state was found by first building and optimising product molecules and then carrying out the transition state analysis. Optimisation was carried out using the same level of theory as with the previous Diels-Alder reaction. As in all of the previous examples an imaginary frequency was found for each transition structure. Table 14 shows the obtained Endo and Exo transition structures and their corresponding vibrations. Bond formation is synchronous as before.
| Conformer | Total Energy/ Hartree | Structure | Imaginary Frequency/ cm-1 | Animation | ||
|---|---|---|---|---|---|---|
| Endo | -0.05150472 | -806.61 | 
| |||
| Exo | -0.05041985 | -812.27 | 
|
HOMO and LUMO of the two transition structures were obtained and can be seen in Table .. The total energy of Endo transition structure was found to be lower than that of the Exo structure. This would suggest that Endo would be a kinetic product with a more stable transition structure. This relative stability could be explained by the secondary orbital interactions of the C-C double bond pi cloud and the -(C=O)-O-(C=O)- fragment. Those interactions are clearly seen in the HOMO molecular orbital of Endo transition structure.
| Conformer | HOMO side view | HOMO end on view | LUMO side view | LUMO end on view |
|---|---|---|---|---|
| Endo | 
|

|

|

|
| Exo | 
|

|

|

|
(This seems to cut out a little early. No mention of sterics, but it seems like you're on the right tracks for secondary orbital overlap Tam10 (talk) 16:55, 24 February 2016 (UTC))
