Rep:Mod:EYAAWKK&^33

3rd Year Chemistry Computational Labs- Physical, Module 3, Experiment 3-Transition States

In this experiment the transition states of Diels-Alder and Cope rearrangements will be studied. The transition states will be characterised by looking at potential energy surfaces of the reactions. In order to do this molecular mechanics methods such as used in module 1 are not sufficient and molecular orbital based methods will be used. This is because unlike molecular mechanics they can describe bonds being broken and formed, and changes in bonding and electron distribution.

In the first tutorial the Cope rearrangement of 1,5-hexadiene will be investigated.

The Cope Rearrangement is a [3,3]-sigmatropic shift type reaction. The reaction proceeds through a concerted cyclic transition state (pericyclic reaction). It is a six electron process and so is allowed under thermal activation. Here is the reaction with arrow pushing shown:

Cope rearrangement

Specifically the Transition State (TS) of the reaction will be looked at in this experiment. The transition state can either be in a boat of chair type conformation and both of these transition states will be looked at using a variety of methods.

Optimising the reactants and products

Initially a molecule of 1,5 hexadiene is drawn into gaussview with an anti (180degrees) linkage across the central four atoms and the structure is cleaned up. This structure is then optimised using the Hartree-Fock method using the 3-21g basis set. The 3-21g basis set uses gaussian distributions in order to define the radial distibution functions. The first peak has three gaussians used in order to approximate it and then the next two peaks two and one respectively. In order to do this the following script is used at the top of the input:

# opt hf/3-21g

The energy of this conformer is -231.69260237 Hartree.

Then the symmetry of this conformer is found by going edit-->symmetrize. The symmetry of this conformtion is C₂.

Next another molcule is optimised at the same level but this time is given a gauche (60 degrees) linkage. One might expect that the gauche conformers would generally be higher in energy than that of the anti-linkage. This is due to steric reasons where the groups would preferably be furthest away from each other as possible.

The energy of this conformer is -231.69166702 Hartree.

The symmetry of this conformer is C₂.

It does turn out to be the case that the anti is the lower energy of the two tried conformers. This is naive to believe this is definative however as there is a lot of conformational flexibility about the molecule even when this central C-C bond has its defined angle.

So in order to find the lowest energy conformer one would expect it to be anti, and with the side-chain groups as far apart as possible. This idea was trialed and resulted in a conformer with the following information:

The energy of the structure: -231.69253526 Hartree

The symmetry of this conformer: C_i

This energy is not the lowest energy (in agreement with the lab instructions). All energies found also match up with the values in the lab instructions. A couple more conformations are trialed also. These energies also matched with the lab script values. It turns out contrary to what is expected that in fact a gauche conformer (furthest right on below table) it lowest in energy. This is due to an electronic effect where being in the gauche conformation allows for favourable orbital overlap that is not present in the anti form. The stabilising interaction is between the vinyl proton and pi-bonds.

Here is a summary of all the molecules trialed:

-	Conformation 1	Conformation 2	Conformation 3	Conformation 4	Conformation 5
Energy	-231.69260237	-231.69166702	-231.69253526	-231.68907066	-231.69266122
JMol
Symmetry	C2	C2	Ci	C2h	C1
Angle of central C-C-C-C bond (Anti/Gauche)	Anti (-176.892 degrees)	Gauche (-64.176 degrees)	Anti (-179.997 degrees)	Anti (180.000 degrees)	Gauche (67.692 degrees)

Now the C_i energy conformer has been identified it will be optimised more accurately using a better basis set. The basis set that will be used is the 6-31g* (or 6-31g(d)) under the DFT B3LYP method.

This was ran using the script:

# opt b3lyp/6-31g(d)

The result of this lead to an energy of: -234.61170273 Hartree

It really isn't fair to compare energies between different basis sets but the geometries can be compared. This will be done by comparing the 5 C-C bond lengths and by comparing the 3 dihedral angles in the molecule:

-	HF/3-21g	B3LYP/6-31g(d)
Bond length 1 (C=C)	1.31614	1.33351
Bond length 2 (C-C)	1.50893	1.50409
Bond length 3 (C-C central)	1.55300	1.54807
Bond length 4 (C-C)	1.50893	1.50409
Bond length 5 (C=C)	1.31614	1.33351
Dihedral angle 1 (C=C-C-C)	-114.669	-118.522
Dihedral angle 2 (C-C-C-C)	180.000	180.000
Dihedral angle 3 (C-C-C=C)	114.669	118.522

It can be seen that using this higher level basis set/method has made slight changes to the bond lengths but the most significant change that is seen is in the dihedral angles 1 and 3 which have changed noticeably. This shows that it is worth running the higher level basis set/method in order to get a more accurate idea of the minimum energy conformation's geometry.

In order to be able to compare calculated energies with experimental quantities furthur terms are needed and these can be found by running a frequency test on the molecule. This was again done at the same level of theory as the last calculation but the script was edited to read:

# freq b3lyp/6-31g(d)

In the "thermochemistry" section of the output log file different types of energies can be found as follows:

Sum of electronic and zero point energies: -234.469211 Hartree

Sum of electronic and thermal energies: -234.461854 Hartree

Sum of electronic and thermal enthalpies: -234.460910 Hartree

Sum of electronic and thermal free energies: -234.500826 Hartree 

Each of the energies given above include different types of thermodynamic information. The first energy is the potential energy (at 0K) and also includes the zero point energy. The second term then includes the energy at 298.15K/1atom (or defined T/P) plus contributions from vibrational, rotational and translational energies. The third includes a correction made for the the fact that H=E+RT and the third includes a contribution from the entropy (G=H-TS).

These energies can be useful to look into the thermodynamics of reactions or indeed kinetics if similar calculations are run on transition state.

These quantities can also be calculated at 0K. This is done by including Freq=ReadIsotopes in the gaussian input file:

# freq=ReadIsotopes b3lyp/6-31g(d)

also at the bottom of the file has to have extras added to define the temperature and the atomic masses of the atoms in the format:

  blank line
350.0 1.0 temp pressure [scale]
12.0 isotope mass for atom 1
1.0 isotope mass for atom 2
1.0 isotope mass for atom 3
1.0 isotope mass for atom 4
2.0 isotope mass for atom 5
  blank line 

which looked like this for this molecule (at 0K and with C=12.0 and H=1.0):

0.0 1.0
12.0
1.0
1.0
12.0
1.0
1.0
12.0
1.0
12.0
1.0
12.0
1.0
1.0
12.0
1.0
1.0

The above energies can be now seen after running this script as:

Sum of electronic and zero-point Energies=           -234.468774

 Sum of electronic and thermal Energies=              -234.461428

 Sum of electronic and thermal Enthalpies=            -234.460483

 Sum of electronic and thermal Free Energies=         -234.500376

However it turns out that this script didn't actually run the calculation at 0K (actually at 298.15K) but in fact just changed the isotopes mas values according to the above values rather than using the gaussview more accurate values. This is why indeed the energies have changed but it is not due to the temperature change.

Freqchk was then used to try and find these 0K values instead. During using this is was found out the reason the above didn't "work" as it should have is that when 0 is entered in temperature it means set T to 298.15K. In the knowledge of this the previous method was used (more familiar) but with T set to 0.00001K. Here is the result of this:

DOI:10042/to-1150

Sum of electronic and zero-point Energies=           -234.468774

 Sum of electronic and thermal Energies=              -234.468774

 Sum of electronic and thermal Enthalpies=            -234.468774

 Sum of electronic and thermal Free Energies=         -234.468774

Thus running the calculation at effectively 0K gives back the same results for all the energies (as one might expect given that all thermal contibutations will be 0) and is equal to the Sum electronic and zero-point energies.

This can be adapted furthur to change the temperature and pressure in any way (e.g. 1atm and 400K).

DOI:10042/to-1151

Sum of electronic and zero-point Energies=           -234.468774

 Sum of electronic and thermal Energies=              -234.456651

 Sum of electronic and thermal Enthalpies=            -234.455384

 Sum of electronic and thermal Free Energies=         -234.514753

Looking at these obviously the temperature effects have been reintroduced on the energies. The sum of electronic and zero-point energies (0K) obviously doesn't change. The electronic and thermal energies/enthalpies are less negative than in the 298.15K case (addition of additional positive thermal corrections; rotational, vibrational and rotational energies or RT) and the Free energies is more negative at 400K than in the 298.15K case (G=H-TS) due to the more negative -TS term.

Overall this section has shown how the freq calculations can be used in a useful manor to acquire additional energy information about molecules (or TS). Also is is easy to modify the T, P or isotope masses to change the result of the calculation and so to study possible reaction information under different conditions. This could be used potentially to find out what may be required to may a reaction work kinetically (if TS is studied) or thermodynamically.

Optimising "Chair" and "Boat" transition States

In this section transition states will be optimised for this Cope Rearrangement reaction. This will be done by several different methods to demonstrate the number of ways in which it can be done.

The first method involves setting up an allyl fragment and then optimising it using the HF/3-21G level of theory. This fragment is then copy and pasted into one MolGroup. These fragments are then aligned in the window as to roughly resemble the form of the transition state. The distance between the terminal ends of the fragments is set to approximately 2.2 angstroms.

This is then optimised to a TS (Berny) using the 3-21g basis set (Hartree-Fock). Also the frequency analysis of this transition state is run simultaneously. The script used to run this type of calculation is then:

# opt=(calcfc,ts,noeigen) freq hf/3-21g

This resulted in a TS for this reaction.

This resulted in a transition state with the following measurements:

Bonds that are going to be formed lengths: 2.02074/2.02084 Angstroms

Negative frequency value of: -818.05 cm^-1

Energy of: -231.61932239

The next way to do this is to use the "frozen co-ordinate method". Going back to the unoptimised structure the Redundant co-ordinate editor was utilised to freeze the terminal ends of the allyl fragments at the approx. 2.2 angstroms previously set. The ends of the allyl fragments that will react are selected and then defined as a bond and freeze co-ordinate is selected. This is done for both ends of the reacting fragments. This structure is then optimised to a minimum (not TS) using the HF/3-21g method/basis set:

#opt=modredundant hf/3-21g

The output structure is then taken and the same atoms that were defined as: Bond-->Freeze Coordinate are now defined as Bond--> Derivative.

This is then ran as before in a transition state optimisation in order to yield the final transition state structure. The only difference in this case is that the force constants are set to calculate never.

# opt=(ts,modredundant,noeigen) freq hf/3-21g

Bonds that are going to be formed lengths: 2.02066/2.02073 Angstroms

Negative frequency value of: -817.726 cm^-1

Energy of: -231.61932240 Hartree

This has shown that in this case the two methods converge well to an answer. This is not suprising given the simplicity of the reacting fragments and the little conformational freedom they have. The fragments will optimise on the freeze-coordinate calculation to really no different to the input allyl fragments conformation. Hence the high agreement between the answers.

The negative frequency in this case shows that this is transition state. Also the form of this vibration is such that it shows the formation and breaking of these bonds in this reaction. This can be seen in the schematic below:

Negative Vibration in Transition state

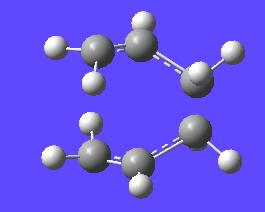
The next thing that will be found is the boat transition structure but this will be done using a completely different method. The method that will be used is QST2. This interpolates between the reactants and products in order to find the transition state between the two.

Nb: I is important that the correct numbering system is used in both the reactants and products in order to get a correct result from the calculation.

The conformation that will be used initially for the reactants and products is the lowest energy C_i found previously.

Here are the products and reactants before the calculation is run (note it is very important how these are numbered to the calculation:

The method selected is the QST2 method and the job type "opt+freq". Also rather than being optimised to a TS(Berny) it will be optimised to TS(QST2).

The result from this calculation is a failure and looks rather like a chair transition state but furthur apart (distance of 3.08631angstroms).

In order to rectify this the conformations of the starting strutures are changed such that the previously "anti" angle is changed to 100 degrees. Here is now what the reactants and products look like before the calculation:

The calculation is ran and here is the resulting "boat" transition structure:

This also has a similar negative vibration as in the chair case. The frequency in this case is at -830.382cm^-1. This again shows the bonds forming and breaking.

The energy of this TS is -231.60280206 Hartree.

This method can be improved on by using the QST3 method in which a guess for the TS is entered into the calculation. This ,ethod often yields a better result. This was done such that the guessed TS was a boat type structure with forming bonds of around 2.2 angstroms. This can be seen below:

The script used to run the calculation is:

# opt=qst3 freq hf/3-21g

The resulting TS was indeed a boat shape structure. The two different TS can be compared in terms of their important characteristics of energy, forming bond lengths and negative frequency value:

-	QST2	QST3
Frequency/cm-1	-830.382	-840.178
Energy/Hartrees	-231.60280206	-231.60280183
Forming Bond lengths	2.13994/2.13994	2.13903/2.13927

This shows that infact that, although the QST3 method most likely produces the most accurate transition state, in this simple scenario the difference between the two is quite small. There is one major advantage to using QST3 and that is that the reactants and products do not need to be modified in order to find the TS (as in the failed example earlier). To back up that the QST3 method finds the more accurate TS, the energy of the QST3 TS is lower in energy than the QST2 TS by 0.0001443 kJmol^-1. Although marginal (showing the similarity of the results of the methods in this case) it does indeed find a lower energy TS.

The next thing to do is to look at Intrinsic Reaction Coordinate (IRC). This calculation will take a transition state and then take small geometrical steps in the direction in the steepest slope of the potential energy surface. This will find then the conformers which the TS connects. This will be done onthe chair TS. This was intially done such that it was only computed in one direction (forward), with force constants caluclated once and for 50 points such that the script used was:

# irc=(forward,maxpoints=50,calcfc) hf/3-21g 

The output from this ended prematurely (but only slightly) at 43steps of the calculation. The reason for this termination is a Link 9999 error in which the gradient of energy to displacment gets too small. However given this got very close to the end number of cycles this was not directly re-run. Here is an image of the IRC calculations energies and RMS gradients throughout the calculation for this case:

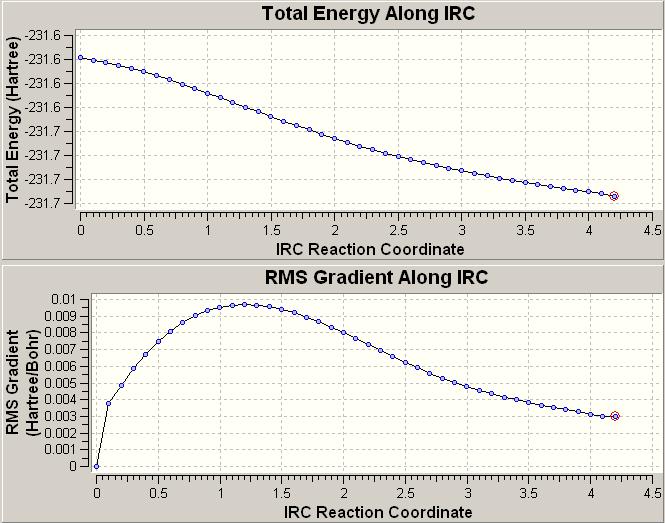
The next step that was taken was to simply optimise the last found geometry in the last calculation this using the HF/3-21G level of theory. This then moved to what should be the correct geometry. This resulted in the geometry of the C₂ gauche type molecule as found above. The fact that this is correct is based on the assumption that the IRC had moved the transition state close enough to the minimum in order to find the correct one.

However even though this IRC calculation ended at 43 cycles it looked similar enough to the C₂ gauche isomer in order for it to be recognised as that. This last geometry is then submitted to a frequency test to check for any negative frequencies. This was to test that this geometry was indeed headed for the suspected geometry and not simply a transition state for any other geometries on the potential energy surface. i.e. Since the IRC ran in one direction and found a minimum close to the gauche C₂ geometry there is no reason that in another direction on the surface there is another energy minimum which this geometry after 43 steps could lead to. This is ran and comes back with all positive frequencies showing that this geometry is not a TS. Thus it is likely the gauche C₂ is the geometry the chair transition state links.

In order to test this another method was trialled in order to locate this structure. The only difference is that the force constant was computed at everystep. This is computationally expensive but the most reliable in order to confirm the above. The script used to run this is:

# irc=(forward,maxpoints=50,calcall) hf/3-21g

This calcultion did in fact confirm the above and this time got to the final number of points (50). Doing the calculation in this way not only got rid of the problem the previous calculation had in finishing but also got alot closer to the expected C₂ gauche conformer. Here is an image of the IRC calculations energies and RMS gradients throughout the calculation for this case:

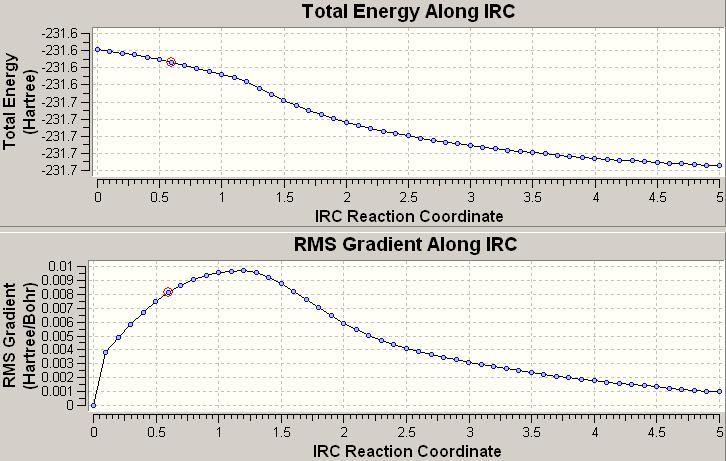
It is interesting to note that the C₂ gauche structure is found using this method and not the lowest energy anti C_i structure that is the lowest energy overall (as seen above). This is because if one follows the IRC it doesn't seem to try an rotate around the gauche C-C bond and thus will not find the anti conformer.

Chair vs Boat Energy

It is not suprising to see then that the chair transition structure is lower in energy than that of the boat transition structure. However to get a more accurate idea of this the final structures will be optimised at a higher level of theory and then can be compared to the lowest energy starting conformer in order to find the activation energy for the reaction for both the chair and boat transition state. This was done along with a frequency analysis and the free energies were extracted from the output files as follows (as well as total potential energies):

Chair Total energy: -234.55698259 Hartree

Sum of electronic and zero point energies: -234.414939 Hartree

Sum of electronic and thermal energies: -234.409017 Hartree

Sum of electronic and thermal enthalpies: -234.408073 Hartree

Sum of electronic and thermal free energies: -234.443825 Hartree 

Boat Total energy: -234.54309287 Hartree

Sum of electronic and zero point energies: -234.402345 Hartree

Sum of electronic and thermal energies: -234.396010 Hartree

Sum of electronic and thermal enthalpies: -234.395060 Hartree

Sum of electronic and thermal free energies: -234.431755 Hartree 

To then calculate the activation energy at 0K simply take the value of the "Sum of electronic and zero point energies"for the reactant (and in this case also product) from the same energies for the transition state (obviously at the same level of theory). In this case the reactant will be the C_i conformer calculated at the higher levwel of theory. Remember also that there is only one activation energy for ths reaction going backwards and formwards as the reactant and product are the same.

The result of this is:

Chair activation energy = 0.054272 Hartree = 34.056 kcalmol^-1

Boat activation energy = 0.066866 Hartree = 41.959 kcalmol^-1

These match fairly well to the experimental values of 33.5 ± 0.5 kcal/mol 44.7 ± 2.0 kcal/mol and shows that the TS calculation is good at predicting real experimental values at this level of theory.

This can also be done at 298.15K this time using the final "Sum of electronic and thermal free energies"

This energy takes into account the entropic contibution to the energy (Gibbs Free energy). This results in:

Chair activation energy = 0.057001 Hartree = 35.767 kcalmol^-1

Boat activation energy = 0.069071 Hartree = 43.343 kcalmol^-1

Also another way of doing this is to look at the "Sum of electronic and thermal enthalpies". Giving:

Chair activation energy = 0.052837 Hartree = 33.156 kcalmol^-1

Boat activation energy = 0.06585 Hartree = 41.322 kcalmol^-1

These calculated values indeed match exactly with the found script values (only given in the script for the 0K and 298.15K wth out entropic contribution). This shows that these results are repeatable which means using these methods is always going to give the same result for a given conformer/TS.

Looking at the final energies then one would expect that the reaction would prefer to go kinetically through the ower energy chair TS. Thus the kinetically controlled reaction would see the reaction go through the chair and not the boat TS.

Theory Level

So what difference has using B3LYP/6-31G* made to the energy and geometries of the transition states when compared to the 3-21G level?

The following table summarises the found energies and geometrical information:

-	Chair		Boat
-	HF/3-21G	B3LYP/6-31G*	HF/3-21G	B3LYP/6-31G*
Energy/Hartrees	-231.61932240	-234.55698259	-231.60280206	-234.54309287
Forming C-C bond lengths/angstroms	2.02066/2.02073	1.96904/1.96875	2.13994 in both	2.20772/2.20648
Internal C=C bond lengths/angstroms	1.38924/1.38920 (in each allyl type fragment)	(1.40735/1.40735) and (1.40752/1.40761)	1.38149 in all lengths	1.39320/1039326 (in each allyl type fragment)
C-C-C angle/degrees	120.492	119.949/119.984	121.694	122.262

This simply shows that changing the level of theory really makes little geometrical difference. Obviously the higher level theory is of different geometry and the most accurate but given the difference in energy between the two this is only small.

The energy between the two theories in is case is:

Chair: 2.9378 Hartrees = 1843.41 kcalmol^-1

Boat: 2.9403 Hartrees= 1845.06 kcalmol^-1

This is clearly a large difference in energies given the small change in geometry in each case. Thus it is good to run a quicker lower level calculation to get the rough geometry and then a higher level calculation to get a more tuned geometry and accurate energy. This thinking will be employed in later on calculations.

Diels-Alder Cycloadditions

In this part of the experiment a Diels-Alder reaction will be looked between ethlyene and butadiene:

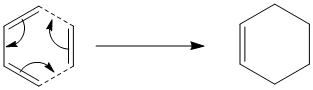
The first thing that is looked at is the butadiene molecule and its MO's symmetries. The molecule is drawn in gaussview and then is put in the cis conformation. This is then optimised using the semi-empirical AM1 method:

# opt freq am1

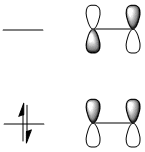
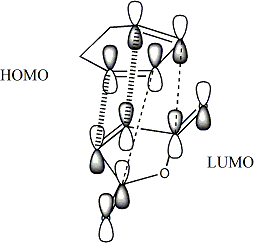
Then once the calculation is run the checkpoint file is opened and the MOs are visualised. Here are the HOMO and LUMO orbitals with their qualitative counterparts adjacent.

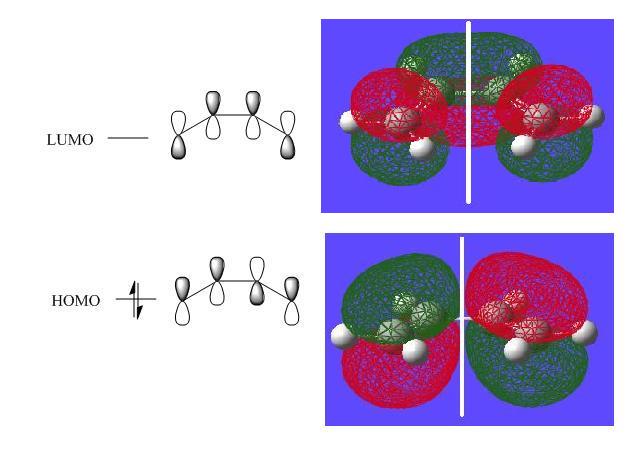
The symmetry of these orbitals can be determined with repect to the plane(as indicated in white in the diagrams above). If the phases of the orbital(s) stay the same phase on reflection in the plane it is symmetric and if they invert it is antisymmetric. Thus the HOMO is anti-symmetric with respect to the plane and the LUMO is symmetric.

A similar analysis of the orbitals can be done in a qualitative fashion also for ethylene yielding:

Here are the calculated MOs also found using the semi-empirical AM1 method:

In this case the HOMO is symmetric with respect to reflection in the plane and the LUMO is antisymmetric. Also note that the HOMO is equivalent to the π-orbital and the LUMO to the π*-orbital.

Next a preliminary reaction is going to be studied in which the transition state of the cycloaddition between ethylene and butadiene will be optimised.

The transition state is set up and the "dashed line" (i.e. where the bond are going to be formed in the reaction) are set to 2.2 Angstroms as in the previous exercise.

The structure is then optimised as in the frozen coordinates method but this time using the Semi-empirical AM1 method. This has resulted in a transition state structure as seen below:

Also a frequency calculation was run on the final structure. There is a negative frequency vibration at -955.579cm^-1. In this vibration the bonds form synchronously between the two fragments. This vibration shows that this is indeed a transition structure. The next highest frequency (now positive) is not related to any bond forming or breaking in the transition state structure i.e. it is simply one of many normal vibrations of the TS.

Here is a still image representation of the negative vibration i.e. the vibration progresses from left to right then right to left etc.):

Negative Vibration of TS

Here is also a labelled diagram of the first positive frequency of the TS (in this case only arrows/vectors indicate the direction of vibration,the larger the arrow the larger the displacement):

One can see that indeed this has no relevance to the bond forming and bond breaking in the TS. However if one had to say whether the motion is synchronous or asynchronous it is asynchronous. The motion can be decribed approximately as the ethylene fragment of the TS moving in a rocking/rotary motion with respect to the butadiene fragment.

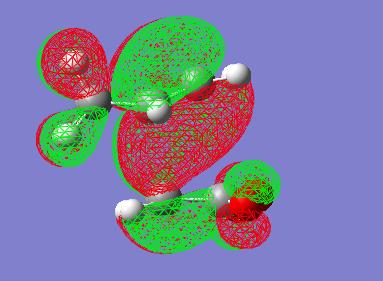
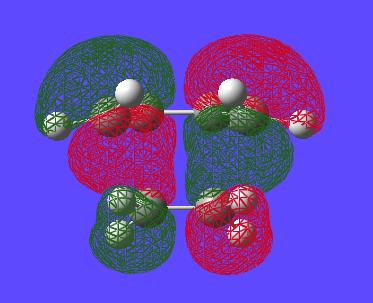
The HOMO and LUMO of the transition state can also be visualised at (Edit--->MOs--->Visualise, then update orbtials that one wants to view):

HOMO	LUMO

An interesting point to note is that if this is ran at a higher level of basis set and method (HF/6-31g) the order of the HOMO and HOMO-1 change. The two orbitals are close in energy in both cases and the HOMO now is:

In terms of symmetry with repect to the plane the HOMO before was antisymmetric with respect to the plane and now (at HF/6-31g) it is symmetric with respect to the plane. The LUMO, which doesn't change on changing method/basis set, is symmetric with respect to the plane. In terms of frontier orbital analysis the first HOMO is equivalent to the reaction of the HOMO of butadiene (antisymmetric with respect to the plane) with the LUMO of ethylene (antisymmetric with respect to the plane)and in the second case is the HOMO of ethylene (symmetric with respect to the plane) reacting with the LUMO of the butadiene (symmetric with respect to the plane). Thus in each case the symmetries of the orbitals must be the same to overlap and react (as one might expect) and the resulting HOMO of the TS also has the same symmetry as the orbitals overlapping to form it.

This reaction is an allowed reaction because it is a 6 electron process (4n+2) under thermal conditions. This can be looked at another way in that in both of the possible TS HOMOs (depending on the level of theory) allow the reactants HOMO and LUMO to line up in a suprafacial fashion (no antarafacial components needed). i.e. the HOMO and LUMO orbtials of the two reacting molecules can overlap in such a fashion that the phases match and the reaction is allowed to occur. The reaction will go in a disrotatory fashion and would be seen evident in a substituted system.

It has also been seen that there is a sensitivity to the HOMO HOMO-1 ordering in the TS depending on method/basis set used. This shows how close in energy the HOMO and HOMO-1 are in this case such that their order can be changed easily by changing the theory level. This could be compared to a situation (as in the next studied reaction) where increasing the level of theory doesn't change the ordering of the HOMO/HOMO-1. Also if one were to put electronegative groups on either the diene of dienophile one might make certain which of the highest two occupied levels is the HOMO; defining the "electron rich" and "electron poor" species in a Diels Alder would make clear which of the reactants HOMO LUMO is reacting and thus which of the top two occupied levels in the TS is the HOMO even at the lower levels of theory.

The bond forming C-C sigma bond lengths can be measured in both levels of theory.

AM1

Length= 2.11900/2.11948 angstroms

HF/6-31g

Length= 2.20341/2.20406 angstroms

These forming bodn lengths are very similar in each method again showing the synchronoous nature of the bond formations. There is also a change in these forming bonds lengths in changing the theory, which ultimately makes no difference to the qualitative aspects of the TS geometry but shows that increasing the theory makes a significant ~1 angstrom difference between the forming bonds in the TS. It ahs been shown that in terms of MO analysis above however that increasing the level of theory is important in determining the true HOMO of the TS.

These distances can then be compared to C-C bond lengths in sp³ and sp² carbons aswell as with the van der waals radius of carbon. These values are:

C-C sp³: 154pm

C=C sp²: 133pm

C Van der Waals radius: 170pm

In all cases these forming sigma bonds are longer. This shows that the "bonding" of the carbon atoms in the TS is not not in realms of a proper covalent bond however it smaller than the sum of two carbons van der waals radii (3.4angstroms). The van der waals radii for C doubled is the closest two carbon atoms can get without forming a proper covalent interaction. Thus in the TS the bonds forming are closer together than this and so there is some some sort of proper covalent interaction occuring but is not fully bonded i.e. is longer than the C-C and C=C bond distances.

Next a more advanced reaction/transition state can be studied. The reaction is of Cyclohexa-1,3-diene and maleic anhydride in a Diels-Alder type [4+2] cycloaddition reaction. This reaction then has the potential to have an endo or exo product depending on the relative orientation of the approaching fragments when they react.

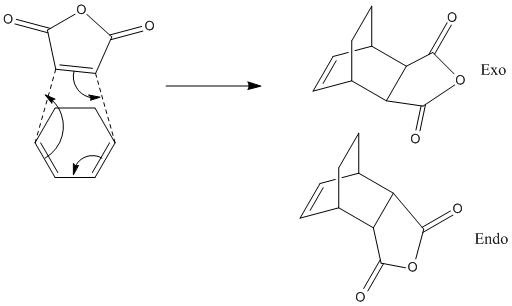
The reaction is supposed to be kinetically controlled. Thus whether the product is endo or exo is decided by the energy barrier to the reaction which can be found by looking at the energy of transition state. The reaction with the lowest energy transition state is the one that will be the dominant product in the reaction.

In each case the TS was set up in gaussview and then the freeze coordinate method was again used in order to find the transition state in each case. The AM1 method was used initally in these calculations.

Here are the found transition states using the AM1 method:

Exo transition state	Endo transition state

Now that these TS structures have been found the HOMOs of each of the molecules can be viewed from the checkpoint file.

-	HOMO	HOMO-1
Endo
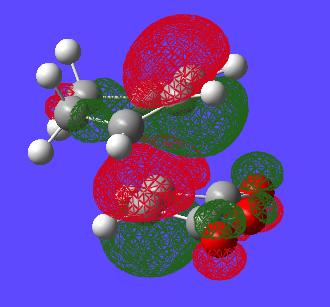
Exo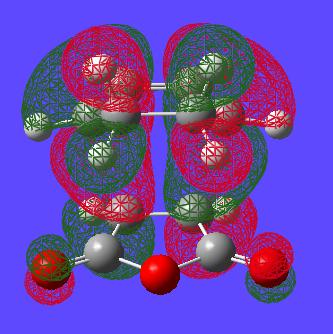

The form of the LUMOs of the two TSs can also be seen visualised below:

-	Endo	Exo
LUMO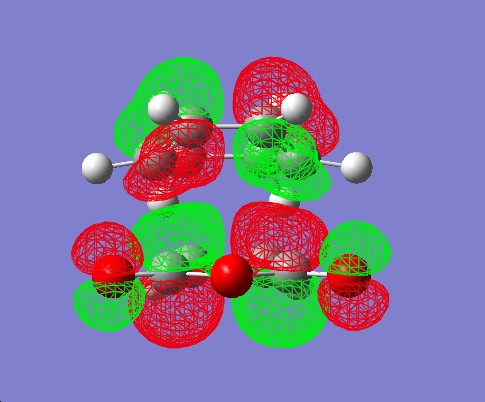

This calculation was run from this end point by increasing the level of basis set to 6-31g (HF)in each case to see if it would (as before) make any difference to the Ordering of the HOMO HOMO-1 of the TS (or indeed the relative energies of the HOMOs and LUMOs in the reacting fragments). Indeed it did not make any difference to the ordering of the levels. Also the overall form of the MOs changed very little with only slight changes thus there is really no need to show them.

In each case the HOMO is antisymmetric with respect to the plane and the HOMO-1 is symmetric for both exo and endo. Also looking at the form of the LUMO in both cases it is symmetric with respect to the plane. Also in both cases the LUMO of the Ts is antisymmetric with respect to the plane.

So these calculated transition states can now be analysed to look at their forming C-C bond lengths:

The distances of the forming C-C sigma bonds are (AM1):

Endo: 2.16242/2.16242 angstroms

Exo: 2.17054/2.17034 angstroms

The distances of the forming C-C sigma bonds are (HF/6-31g):

Endo: 2.22493/2.22415 angstroms

Exo: 2.25165/2.25146 angstroms

The result of the HOMO is interesting because it doesn't fit in with what one would expect from looking at the secondary-orbital interactions analysis of the reaction (discussed in the next section). Thus to ensure that the result is correct the more advanced MP2 level of calculation was run (6-31g* basis set) on the two transition states as to minimise then again to transition states but at a higher level. The MP2 level caluclation takes highly into account dynamic electron correlation which improves the modelling above the previous. This however result again in the energy levels being in the same order as before and so backed up the results from the lower level calulations. The bond lengths of the forming C-C bonds can again be measured at this level.

The distances of the forming C-C sigma bonds are (MP2/6-31G*):

Endo: 2.33892/2.33953 angstroms

Exo: 2.35185/2.35279 angstroms

In both cases given the similarity of the forming bond distances the bond forming is synchronous. This synchronous behaviour can be seen also in the negative vibrations of the TS if they are viewed.

Taking these highest level MP2 level transition states other important distances can be measured and displayed in labelled diagrams:

-	Endo	Exo
Forming C-C bonds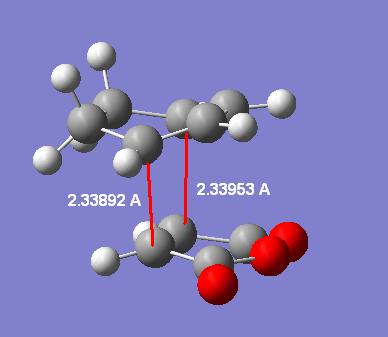
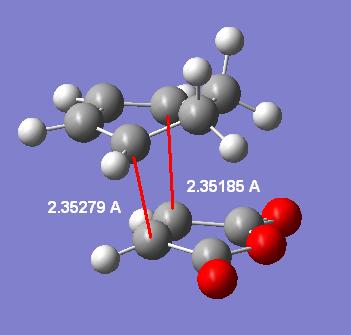
Other C-C bonds

The energies of the endo and exo transition states can also be given (in Hartrees) for each level of theory and compared:

-	Endo	Exo
AM1	-0.05159426	-0.05050326
HF/6-31G	-608.72044758	-608.71380547
MP2/6-31G*	-610.83622437	-610.83087239

In all cases the endo TS is indeed the lowest energy of the two. The difference between the TS in each case is (in favour of endo):

AM1: 0.001091 Hartrees= 0.68461341 kcalmol^-1

HF/6-31G: 0.0064233 Hartrees= 4.030684983 kcalmol^-1

MP2/6-31G*: 0.00535198 Hartrees= 3.35842097 kcalmol^-1

This then shows that indeed if the reaction is kinetically controlled that the major product will be endo. Whether this fits in with the frontier orbital approach will be discussed next.

The exo form of the TS will also have a higher strain than the corresponding endo version. This seems counter intuitive because of the fact that in the endo TS the maleic anhydride ring lays close to the other ring system. However one must consider the hybridisation of the carbon centres laying above the maleic anhyride ring. In the exo case these carbons are sp³ hybridised as oppose to the sp² hybridisation in the endo form. This will then mean the strain in the exo form is higher than in the endo form. Thus the exo form is higher in energy because of the increase of strain and because of the lack of "secondary orbital interaction".

Another measurement that can be made (will be done on the highest level MP2 calculated forms) is the through space distance between the C in the C=O group on the maleic anhydride to the C in the opposite C-C group in the exo and C=C in the endo. Here are the labelled distances:

Endo	Exo

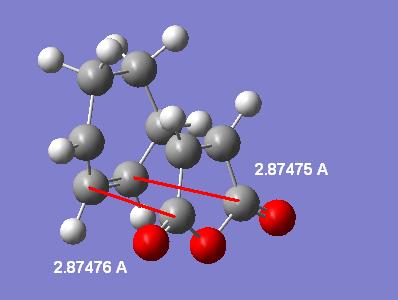
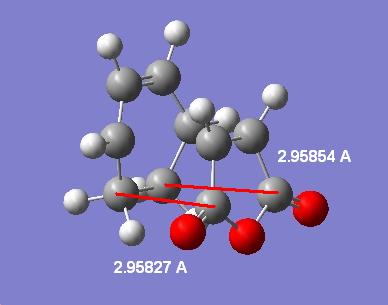
This shows that in the exo case the distance is longer than in the endo case. Despite this the steric strain created in the exo is probably higher than that of the endo due to the aforementioned hybrisation difference. In fact the large distance in the exo is probably down to the higher steric strain. Also since the endo has the "secondary orbital" interactions in the HOMO-1 the pi-CH₂=CH₂ system will be pulled closer to the maleic anhydride O=C-O-C=O fragment.

The hybridisation effect on the sterics can be best shown by looking at the distance between the hydrogens on the opposite to maleic anhydride C-C (exo) or C=C (endo) and the carbons in the O=C-O-C=O moiety. This will again be done on the highest level MP2 forms of the TSs. The resulting distances are 2.97380/2.97366 angstroms in the endo form and a mere 2.44270/2.44341 angstroms in the exo case. This is an average difference of 2.97373-2.443055=0.53 angstroms. This is where the higher sterics in the exo form originates.

Secondary Orbital Overlap

One thing that is interesting to discuss is the theory of secondary orbital overlap. Frontier Molecular orbitals can be looked at easily in order to explain reactivity in many systems. If one looks at the frontier molecular orbtials for the diels alder system one can rationalise why the endo transition state is favoured. This preference for the endo over the exo is explained as a kinetic effect and involves frontier orbitals that are not directly involved in making the bonds in the reaction. In the Endo transition state there are additional orbital interactions that lead to the stabilisation of the transition state.

This can be displayed as shown below (primary interactions shown in bold dashes and secondary in thin dashes):

Is this in agreement with the analysis above of the MOs?

Looking at the HOMO of the endo TS one would expect that the nodal pattern would resemble the qualitative diagram below. In some respects it does actually match up very well but the main problem is that there seems to be no electron density above the maleic anhydride atoms that one would expect to be invovled in the seconday interactions. This can be seen best from the side angle of the HOMO:

However in HOMO-1 there is a similar interaction. It is not from the carbon atoms on the maleic anhydride one would expect from the qualitiative analysis but actually from the oxygen atoms into the forming pi-bond. This could help in increasing the stabilisation of the endo TS thus making it the lowest energy TS. The Exo TS will have no such interaction because the forming pi-bond is not geometricaly in a position where it could occur.

Overall this shows that although Frontier Orbital anlysis is a useful pen and paper method for predicting kinetics in this case, computational analysis of the orbtials show that there is little reality to the analysis. In the HOMO such a "secondary interaction" is not present but is present in a different form in the HOMO-1 rendering the endo TS the lowest energy. So in some respects there is a "secondary orbtial overlap effect" but not in the way FMO theory predicts and utilises.

Both ways of analysing the reaction come to the same result and so although the FMO "secondary orbtial overlap effect" analysis is not 100% true it is still predicts correctly in the ultimate result.

This Secondary orbital interactions analysis are also useful in trying to rationalise the Chair TS being favoured over the boat TS in the cope rearrangement. This can be displayed visually:

Secondary orbital interactions in the Boat-like and Chair-like Transition structure for the Cope rearrangment

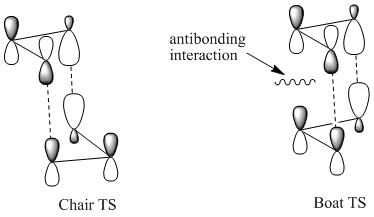
In this case in the boat TS there is an antiboding interaction which is not present in the chair TS. This antibonding interaction obviously raises the energy of the boat TS and thus in a kinetically controlled siutation the TS that would be proceeded through the most would be the chair. This analysis is in line again wit the more complex comutational analysis which did indeed show that the Chair TS is lower in energy than the Boat.

Dimerisation of Cyclopentadiene

In this section the dimerisation of cyclopentadiene will be looked at in terms of exo and endo stability as above and the techniques learned above will be used in order to probe this reaction and look into any phenomena.

Here is the reaction scheme for this dimerisation:

Dimerisation of cyclopentadiene

In order to do this initially the PM3 semiempirical method will be used in the frozen coordination method as before. The transition states were set up and the calculations ran. In the first calculation the script that was run was(note the frozen coordinates at the bottom of the script):

# opt=modredundant pm3

Title

0 1
"Coordinates"
B 12 2 F
B 15 1 F

and then for the TS optimisation:

# opt=(ts,modredundant,noeigen) freq pm3 

Title

0 1
"Coordinates"

B 15 1 D
B 12 2 D

Here are the results for both the exo and endo forms of this reaction at this level of theory:

PM3	Endo	Exo
JMol
Energy/kcalmol-1	100.7593	99.9635
Sum of electronic and thermal Free Energies/kcalmol-1	198.3873	197.5646
Forming bonds lengths /angstroms	2.11906/2.18221	2.12676/2.18408
Negative Frequency/cm-1	-892.335	-898.849

These results are curious in the fact that it is in this case indeed the endo TS that is higher in energy than the exo TS. One thing to notice is that indeed however the asynchronicity of the reaction is larger in the endo TS rather than in the exo TS. This is odd given that the endo product is the one that in fact dominates the reaction. In order to gain more light on this reaction a more advanced calculation was run with a higher level method B3LYP with the basis set 6-31g(d).

The Frozen coordinate method was run again (both opt with frozen coordinates and opt to a TS with derivative/bond as before) at this new level. The results from this calculation are curious and interesting. Before any discussion of the results here are the results from these calculations:

B3LYP/6-31G*	Endo	Exo
JMol
Energy/kcalmol-1	-243581.3359	-243578.504
Sum of electronic and thermal Free Energies/kcalmol-1	-243483.4571	-243480.3346
Forming bonds lengths /angstroms	1.96215/2.89678	2.06333/2.50923
Negative Frequency/cm-1	-377.31	-457.036

These interesting set of results have been published to D-Space:

Endo: DOI:10042/to-1116

Exo: DOI:10042/to-1117

One must notice how in the case of the endo transition state that it in fact highly asynchronous bond forming takes place. The exo transition state is also noticed to be significantly less asynchronous than the endo case. Although in both cases asynchronous character is shown. The difference in bond lengths in each cases is:

Endo: 0.93463 angstroms

Exo: 0.4459 angstroms

After much curiosity into this result and spending time looking for literature into this area, a journal discussing this exact reaction was found . Interestingly enough they had happened also to run this calculation at the same B3LYP/6-31G* level as I. Taking measurements of the geometry of this transition state (lengths exactly matching that of the reference journal's numbers) there is some interesting to note. Here are the labelled important lengths:

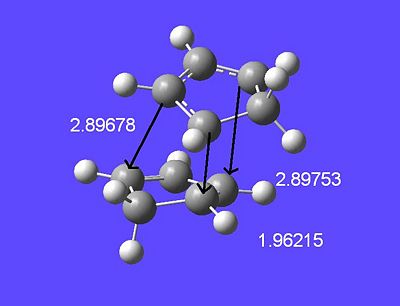
The image seen in the journal that describes possible reactions of cyclopentadiene shows nicely their meausured bond lengths and energies in each case. Note the similarity of the found distances to those found in this experiment:

Energy Profile for reaction

An important thing to notice is the nature of the transition state 7N. The reaction is thought to go through a bis-pericyclic transition state is which there is a [4+2] reaction aswell as a [2+4] reaction in the TS. This can then go from the transition state such that one of the cycloaddition reaction completes and forms a product. The shortest forming bond (1.96 angstroms) shares both of the pericyclic ring systems, which makes sense that this would be the shortest forming bond (strongest interaction between both ring systems).

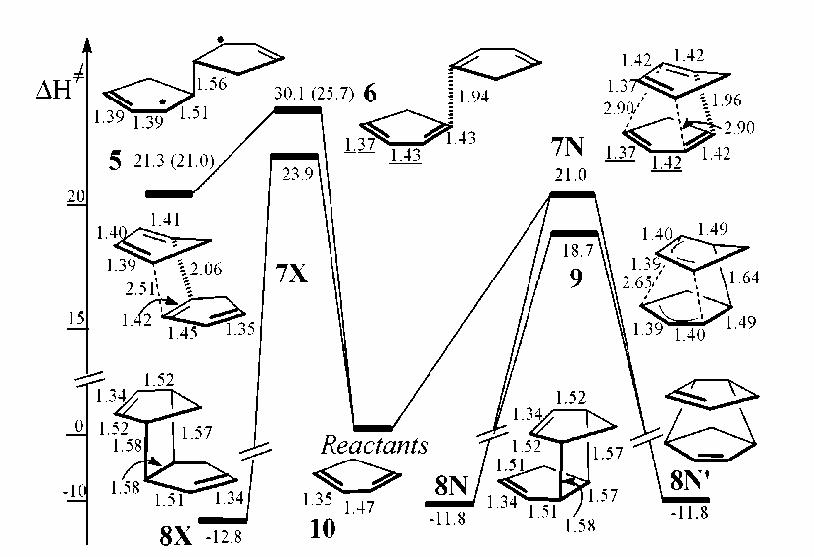
The consequences of the potential energy diagram (2D representation of a surface) will now be discussed. The lowest routes for the dimerization process are through the endo (7N) and exo (7X) TS as investigated in this project and as found the endo is infact the lowest overall. It turns out as expected that the endo dimer is thermodynamically less favourable when compared to the exo. This is down to sterics where the ring are closer together in the endo-product case (more strain) than the exo. As already discussed the shape of the endo TS is the most interesting of the two. The exo although still asynchronous is not anywhere near as pronounced as the endo. An important point to note about the endo TS also is it's C₂ symmetry (also chiral). The endo TS does show some similarities such as bond lengths with the diradical forming TS 6 but is really not the same and is a first-order saddle point along the concerted pathway to the adduct.

IRC calculation run in the Journal show that as the TS moves down the potential energy surface the C₂ symetry is maintained. This calculation was also ran in this project (# irc=(maxpoints=100,calcfc) b3lyp/6-31g(d)) but terminated after only 20 steps. This did indeed confirm the retention of the C₂ symmetry on movement down the surface. After this really the Cope TS 9 must be considered anyway and so any information I wanted from the IRC was received. As the TS heads towards the cope, if it is indeed calculated, the imaginary antisymmetric imaginary frequency of the cope is seen. This vibration breaks the C₂ symmetry of the molecule and allows the reaction to follow the potential surface down to one of the two products (two products are possible form the two different [4+2] pericycles in the TS).

Here is the potential energy surface of the reaction as explained above:

Proposed potential energy surface of the reaction

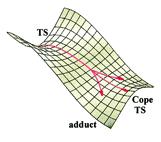
The TS being a mixture of the [4+2]-[2+4] reactions and the diradicaloid appearance of the bipericyclic concerted TS can be explained as follows. The reaction in the exo case is asynchronous as expected due to the polarisation of the orbtials towards the end of the diene units. This can be predicted using Huckel theory. In the case of endo TS it takes advantage of both of these types of stabilising interaction with only a small geometrical distortion. Thus the endo is overall lower in energy than the exo and so the dominant product is endo. The found energies in this experiment can be seen to support this idea next.

The energies of the systems can also be looked at and compared roughly the found literature values. The only difference will be that the journal looks in terms of ΔH whereas this will now look in terms of ΔG ("Sum of electronic and thermal Free Energies")

The reactant cyclopentadiene molecule is ran under the same level of calculation (B3LYP/6-31G*) and the energy found for one cyclopentadiene is: -121758.7535 kcal^-1 or -243517.507 kcal^-1 for two molecules.

Thus the energy change going from the two reactant molecules to the exo transition state is: 63.82889476 kcal^-1

and going from the two reactant molecules to the endo transition state is: 60.99699476 kcal^-1

The energy difference between these two TS is then: 2.8319 kcalmol^-1

This is close to the literature value of 2.9 kcalmol^-1 but one must remember it is the entropy is taken into account in the energies here whereas they were not taken into account in the literature. It is also interesting to note the difference including the entropic contribution makes on the difference between the two cyclopentadienes and the two TS. The values of 23.9 and 21.0 are significantly smaller than that of the values above. This shows how much difference the entropic contribution makes in this case.

In order to investigate the transition state furthur the molecular orbtials of the TS must be visualised, and in particular the HOMO. Here is an image of the HOMO of this endo transition state:

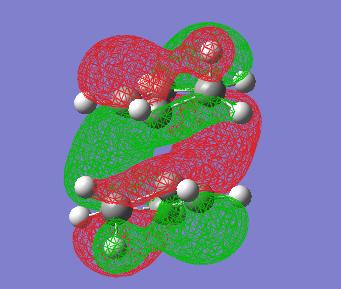
An interesting point to note in the endo-TS is that it is of C₂ symmetry. This can be seen in the above MO picture in which the axis goes through the centre of the two different phases of orbitals. Also one can notice that if indeed a C₂ operation is performed on the TS the HOMO stays the same but the phases invert. It is also interesting to notice that each phase of orbital in the HOMO doesn't infact doesn't resemble the proposed [4+2]-[2+4] systems in the transitions state. Each phase in fact seems to link 3 atoms on one face with 2 atoms on the other face. Thus the mechanism is not as simply explained as FMO theory and arrow pushing would suggest to go through this TS.

The nature of the transition state is also curious because of its nature of being between two transition states but instead of being a second order transition state i.e. a transition state between two other transtion states it is actually a minimum between these extreme [4+2]-[2+4] transition states. This is analagous to some other ground state state situations. A example of this is the norbornane cation, the migration of part of the 6-membered ring to the cation site has a "TS" in which it is the most stable adopted state. This results in a 3c-2e type interaction. This was confirmed with crystallographic data to exist. In order to tell what the true nature of this endo-TS is, is to run a ELF calculation

This analysis of the Endo-TS in this way would then give more light into the nature of the TS itself.

Going back to the unusual nature of this TS being half way between the two other potential [4+2]-[2+4] TS is to be briefly investigated. Below is a diagrammatic representation of the situation (explained afterwards):

The green and black lines show the usual expected siutation of two TSs with a second order TS between them. The green case is just showing a lower activation energy situation than the black.

The red line is showing the case where the point on the reaction coordinate that should be the second order TS is actually the minimum (the case here).

The blue lines are showing a shift of this minimum in either direction such that the minimum is a situation somewhere between the two but not exactly half way. If one was to theoretically keep shifting the blue curve one might expect a second minimum to reappear and revert back to something more like the black and green lines.

In an attempt to switch from one type of regime to another the molecule is altered and the TS recalculated. The TS is given a cyano group on the methylene part of each ring such that the C₂ symmetry of the TS is maintained but the electronic properties altered. Then one can see if this electronic change in the TS will alter the regime i.e. will the prefered TS move such that one [4+2] is prefered over the other?

This calculation was ran but this time with the derivative option on the forming bonds. Thsi resulted in a TS that was actually similar tot he previous and this change did not make a difference to the regime type of the TS. One can look at the important forming bond lengths:

1. 2.01247 angstroms

2. 2.88405 angstroms

3. 2.89146 angstroms

Again this has shown the same phenomena as before. The bond lengths have changed and the amount of asynchronous behaviour in each "pericycle" has decreased marginally however really no major change has occured.

Another proof that this is indeed simply a TS is that in the frequency analysis there is only one imaginary freqency at -370.474cm^-1.

The next attempt into finding this possible second order TS is to actually marginally change the symmetry by introducing a group with difference electronic properties. Then a frequency analysis will be done to look for multiple negative frequencies. If indeed multiple negative frequencies are found this would be evidence of changing to a second order TS. However it turns out that only one negative frequency is identified and so gives no furthur progress to the experiment.

There is an abundance of investigation to be done on this situation however there is no furthur time in this module to continue exploration.

Some furthur calculations run by Henry Rzepa reveled some interesting information also about the TS found. Initially an AIM analysis was run. This analysis identifies stationary points in the actual topology of the electron density rather than in the nuclear potential energy surface. This resulted in the following visualisation:

The red points show bond critical points (which are in the expected positions form the above anlysis of the reaction). The yellow point show ring centroids which are situated in the centra of each ring and also in the centre of where the "two different pericycles" interact. There is also the green cage-point. These so called (3,+3) critical points arise where there is a "local minimum with electron density rising in all 3 directions of space" and form between ring systems i.e. when the interior of a molecule is enclosed with ring surfaces.

Then at these critical points then an NICS analysis at the position of the AIM points (just previously). The found values apparently show that the cage point shows a strongly diatropic ring current. This is at -20 ppm (cf. benzene at -10ppm) which indicates a high level of aromaticity.

There is more research to be done into this area and investigations that could be done in substituting groups on the TS in different places and seeing how this effects the potential energy surface of the reaction. Also running this at different levels of calculations would be useful to find out more about this reaction. There is not enough time in this prject to continue this however and furthur pursueing will have to take place outside the course.

One simple point that was noticed in the end project is that running a simple of level calculation did not reveal the full nature of the Ts and a higher level must be chosen. Thus one must choose the correct level of calculation for each scenario. Also not using the higher level of theory and thus not including the more complex interaction did not explain the dominancy of the endo transition state (endo TS was actually higher in energy) but when it was included the endo TS was indeed the lower in energy of the two TS.

Conclusion

This project first taught methods of optimisation of molecules and transition states. These calculations throughout the project were ran in various different methods and then compared and contrasted. These techniques were applied to various different examples and then spring boarded into a project at the end involving cyclopentadiene dimerisation. This project used previously learned techniques to apply to the reaction and interesting properties of the dimerisation reaction were found. This simply shows the useful nature of computational techniques in this case where this phenomena would not have been found without them. Of course it is also important to approach any findings with caution and furthur investigation.

Overall a successful project and learning how to calculate transition states will be extremely useful for future work and projects.