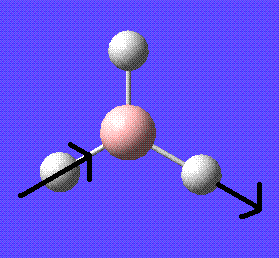Rep:Mod:EYAAWKK&^2

Computational Labs- Inorganic Module 2

Introduction and Day 1

In this module the first thing that will be done is to become familiarised with gaussview. This will be done by drawing and manipulating a molecule of BH₃.

After drawing the initial molecule (before optimisation) the bond lengths and angles are:

B-H Bond lengths: 1.18 angstroms

H-B-H Bond angles: 120 degrees

Next all the bond lengths were set to 1.5 angstroms using the bond distance "button".

An optimisation (OPT) calculation was then run using the B3LYP method and 3-21G basis set.

The output can molecule was then opened as a .log file and the following information was measured:

B-H Bond lengths: 1.19435 angstroms

H-B-H bond angles: 120 degrees (as expected from VSEPR theory)

The Summary for the calculation can be seen below:

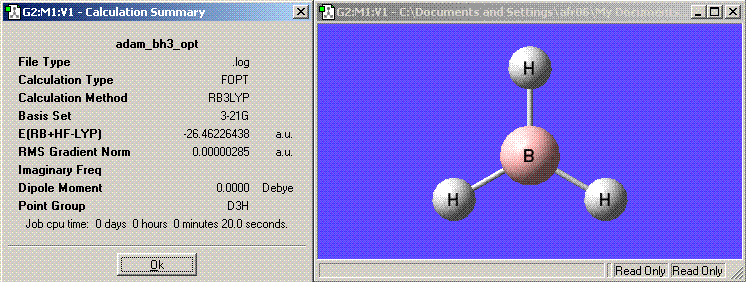
from this summary the following information about the calculation can be extracted:

The file type: .log

The calculation type: FOPT

The calculation method: RB3LYP

The basis set: 3-21G

The final energy in atomic units (au): -26.46226438

The dipole moment: 0.0000 Debye

The point group of your molecule: D_3h

Time of calculation: 20.0seconds

Also the actual .log output file can be opened thorough Gaussview and can be seen in the screen shot below:

This next part of the introduction will look at using psuedo potentials and larger basis sets in order to run calculations. The molecule which will be investigated using these techniques in BCl₃. This is done by adding in the boron trigonal planar fragment and then the hydrogens changed by clicking on them whilst the Chlorine atomic fragment is selected.

This will now be optimised in gaussview as in the prevous molecule. However this time a different medium-level basis set of LanL2MB will be used (instead of 3-21G also still using the B3LYP method).

After running the optimisation calculation the bond lengths and angles are:

B-Cl bond length: 1.86592angstroms

Cl-B-Cl angle: 120 degrees

The information extracted from the summary can be seen below:

The file type: .log

The calculation type: FOPT

The calculation method: RB3LYP

The basis set: LanL2MB

The final energy in atomic units (au): -69.43928112

The dipole moment: 0.0000 Debye

The point group of your molecule: D_3h

Time of calculation: 11.0seconds

Next just to complete the introduction a small molecule will be created and optimised. The molecule that this will be done to is CO₂. The molecule is first drawn into ChemDraw and then optimised using the B3LYP method with the 3-21G basis set.

The output summary for the optimisation log file can be seen below:

again from this summary and using the inquire tool the following information about the molecule and calculation can be extracted:

The Final output Co-ordinates for the optimisation can be seen below:

 ---------------------------------------------------------------------
Center     Atomic     Atomic              Coordinates (Angstroms)
Number     Number      Type              X           Y           Z
---------------------------------------------------------------------
   1          6(Carbon)     0        0.000000    0.000000    0.000000
   2          8(Oxygen)     0        0.000000    0.000000    1.182781
   3          8(Oxygen)     0        0.000000    0.000000   -1.182781
---------------------------------------------------------------------

C-O bond length: 1.18278angstroms

O-C-O angle: 180degrees

The file type: .log

The calculation type: FOPT

The calculation method: RB3LYP

The basis set: 3-21G

The final energy in atomic units (au): -187.52363688

The dipole moment: 0.0000 Debye

The point group of your molecule: D_∞h

Time of calculation: 13.0seconds

Next a frequency calculation will be ran on BH₃. The previously optimised molecule is opened in gaussview and then a gaussian calculation in run.

After the freuquency calculation is run the energy is left unchanged from before the calculation which is good. The vibrations are now visualised (Results-->Vibrations) by selecting a vibrational frequency and then clicking start; displacement vectors are turned on by checking the "Show Displacement Vectors" box.

The analysis of these 6 vibrations can be seen in the table below:

Vibration number	Form of the vibration	Frequency	Intensity	Symmetry D3h point group
1		1145.71	92.6991	A"2 (wagging)
2		1204.66	12.3789	E' (H-B-H Scissoring)
3		1204.66	12.3814	E' (H-B-H Scissoring/rocking)
4		2592.79	0	A'1 (B-H symmetric stretch)
5		2731.31	103.837	E' (B-H asymmetric stretch)
6		2731.31	103.83	E' (B-H asymmetric stretch/symmetric stetches)

These assigments can be confirmed by literature in which the stretching frequencies of BI₃ are assigned. The reason for using this BI₃ is simply that is exists in its monomeric form due to the donation of electron density into the borons vacant p-orbital, whereas BH₃ exists as dimers (B₂H₆). This makes no difference however as the symmetry of the vibrations will be the same.

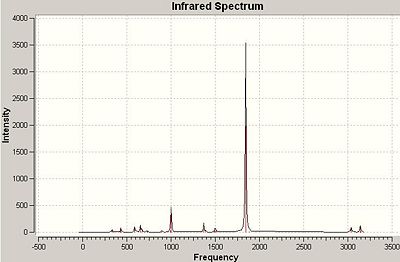
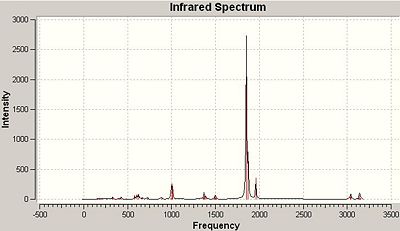
Here is also an image of the IR spectrum of the molecule:

It can be seen that the vibration number 4 can't be seen in this spectrum. This is simply because there is no change in dipole moment in this this vibration and therefore is not seen in an IR spectrum (intensity=0).

Next the Molcular orbitals that were calculated during this optimisation and frequency calculation can be visualised in gaussview. The MOs can be seen below alongside there qualitative counterpart:

Nb: The qualitative MO diagram construction of BH₃ can be found below the table.

Orbital	Computed MO Visualisation	Qualitative generated MO
MO 1
MO 2
MO 3 (degenerate HOMO)
MO 4 (degenerate HOMO)
MO 5 (LUMO)

Here for comparison to the generated calculated orbitals is a constructed ChemDraw MO diagram for BH₃. This was constructed by looking at the AOs that would be expected to contribute to making the molecule and then interacting molecules with the same symmtery to form a bonding anti-bonding pair. Remember that the closer in energy an AO is to the MO it forms the more it contributes to the overall form of the MO.

One thing to consider is the difference between the qualitative and quantiative MOs. Looking at the calculated orbitals above next to their qualitative counterpart there are no major differences between the predictions between the two. Obviously one must take the qualitative MOs and imagine how the AO, how they are drawn, would interact in the MO they have created e.g. in the qualitative MO with all the s type orbitals in phase one must imagine they would interact with each other to give a triangular shaped orbital (as seen in the calculated orbital). This whole qualitative process can be done pen and paper with a bit of logic and intuition and give very good matches to the calculated orbital. This can be done in a short time and without the need for a computer. Also the extent of contribution of each AO to the MO it forms can be determined qualitatively. The closer the AO to the MO it forms the more it contributes to the form of this MO. This renders qualitative MO theory very useful overall. However to get quantitative energies of the MOs, as well as a better idea of the overall shape, atomic orbital coefficients in the MO and extent of mixing one must use quantitative MO calculations.

Another difference that must be noticed is that LUMO (really being the p_z) is very large (more diffuse) and is acutally covering the hydrogen atoms. This is because in calculating the MOs the unoccupied orbitals aren't calculated accurately as really only the occupied orbitals in the ground state are important in the calculation and so represented well.

Day 2

In this part of the experiment the metal complex molecules trans-Mo(CO)₄(PMe₃)₂ and cis-Mo(CO)₄(PMe₃)₂ are investigated.

The first thing to do is to draw the molecules in ChemBio3D (simply for ease of constructing the molecule) and then optimisation calculations are run on the molecules.

The initial calculation is fairly crude and uses only the LANL2MB pseudo potential and basis set (in the DFT B3LYP method) according to the script:

"# opt b3lyp/lanl2mb"

A psuedo potential is useful for larger elements because instead of doing a quantum mechanical calculation on all electrons the innner electrons (which don't dominate the bonding) can be treated using a simple Pseudo-potential (effective core potential). Using these potentials to model the inner electrons are much quicker and easier than doing the full calculation and give an accurate enough answer. These sort of basis sets and potentials also include d-orbitals for the heaver elements. The Lanl2dz basis set/pseudopotential (used next) is an improvement (higher level basis set) on the Lanl2mb basis set/psuedopotential. The details of these can be seen below:

LanL2MB: STO-3G on first row, Los Alamos ECP plus MBS on Na-La, Hf-Bi.

LanL2DZ: D95V on first row, Los Alamos ECP plus DZ on Na-La, Hf-Bi.

The output from the previous optimisation is then optimised in more precised way using a more complex LANL2DZ basis set/psuedopotentental.

This optimised output is then optimised again again more precisely by adding to the addition keywords: "int=ultrafine scf=conver=9"

Now the optimised geometries is each case in known the obtained structures can be analysed and compared to literature. Also a frequency calculations were carried out using the following script:

"# opt freq b3lyp/lanl2dz geom=connectivity int=ultrafine scf=conver=9"

trans-Mo(CO)₄(PMe₃)₂: Structure uploaded to D-Space; unique identifier:DOI:10042/to-989

cis-Mo(CO)₄(PMe₃)₂ [CAS:016927-45-5]: Structure uploaded to D-space; unique indentifier:DOI:10042/to-990

The important (CO stretching)resulting frequencies from these two optimised structures can be seen in the table below:

Trans
Vibration	Frequencies/cm-1	Intensity
CO	1838.86	2000.82
CO	1838.97	2004.42
CO	1882.89	1.1525
CO	1954.63	0.4769

Cis
Vibration	Frequencies/cm-1	Intensity
CO	1848	1069.52
CO	1850.29	1960.65
CO	1869.45	666.022
CO	1960.07	321.252

After looking at these frequencies a furthur more advance optimisation calculation was run in the molecules as to include the d-orbital contribution that the phosphorous atoms would have in reality which were not taken in to account before. These low lying d-orbitals one would expect to have an effect on the geometry and stretching frequencies as they get involved in the bonding of the molecules. Gaussview does not have the direct options in order to be able to make these adjustments. However the script can be directly edited as to make these adjusments. The final output geometries were taken from the previous calculations and then re-submitted for calculation with the following adjustments:

The first line was put as "# opt b3lyp/lanl2dz geom=connectivity extrabasis int=ultrafine scf=conver=9"

and at the bottom of the input was inserted:

(blank line)
P 0
D  1  1.0
0.55  0.100D+01
****
(blank line)

This simply tells the "extrabasis" part of the input to add a D-function (line 2) to the P atom (line 1) with a specific width (0.55) and decay rate (0.100D+01).

Once this was run in each case the geometries can be interpretted and the frequency calculations ran:

"# freq b3lyp/lanl2dz geom=connectivity extrabasis int=ultrafine scf=conver=9"

Here is just one MO visualisation from the calculation checkpoint file which shows the d-orbital type interation on the phosphorous atom:

The important resulting frequencies can be seen in the table below:

Trans (with d-orbitals)
Vibration	Frequencies/cm-1	Intensity
CO	1843.9	1978.92
CO	1844	1983.25
CO	1884.94	5.4546
CO	1956.4	1.9324

Cis (with d-orbitals)
Vibration	Frequencies/cm-1	Intensity
CO	1851.03	1949.02
CO	1854.59	1040.08
CO	1873.2	675.906
CO	1959.65	351.988

Here is a summary of important parameters that are found in both the cis and trans form of the molybdenum complex with and without d-orbitals. After this an analysis of the accuracy of the method and the importance of d-orbitals in the calcualtion will be discussed. Literature values are also displayed in the table below. For the cis-complex an exact molecule match could be found, but in the trans case the tri-phenyl phosphine complex could only be found (not trimethylphosphine). This should however give a good idea of the accuracy of the calculation anyway.

Molecular Geometric Parameters	Trans	Cis	Trans (d-orbitals)	Cis (d-orbitals)
Av. P-Mo Bond length (angstroms)	2.57163	2.64990	2.525115	2.590945
Av. P-Mo Bond length (angstroms) lit	2.500	2.522	2.500	2.522
Av. C-Mo Bond length (angstroms)(cis to phosphine)	2.028655	2.03247	2.030035	2.031865
Av. C-Mo Bond length (angstroms)(cis to phosphine) lit	2.011	2.032	2.011	2.032
Av. C-Mo Bond length (angstroms) (trans to phosphine)	N/A	1.98200	N/A	1.993475
Av. C-Mo Bond length (angstroms) (trans to phosphine) lit	N/A	1.9705	N/A	1.9705
Av P-Mo-P angle (degrees)	178.938	95.3	178.044	96.643
Av P-Mo-P angle (degrees) lit	180.0	97.54	180.0	97.54

One can compare the accuracy of the calculated values to the actually determined experimental values.

First looking at the cis isomer because the literature values can be found for the exact compound. Firstly the Mo-P bonds match up well. In this case the best bond length match is when the d-orbitals are included in the calculation. Initally the Mo-P bond is too long (5.07% difference). Then including the d-orbitals in bonding the bonds are made shorter (back-bonding increases bond strength) and closer to the literature (although still too long). The percentage difference is a mere 2.7 % which shows how good the modeling is at predicting this bond length.

Next the C-Mo (cis to phosphine) bond length is also a good match. Intially the bond length is a bit large compared to literature when not including d-orbitals (only by a small 0.023%). However including d-orbitals decreases the lengths of these bond such that there is a marginally better argreement between the calculated and experimental values. The percentage difference is 0.0135% from the literature which shows in this case the calculated distances are highly accurate.

The C-Mo (trans to phosphine) has a similar situation to above. Without the d-orbtials the lengths are acutally a better match then when present in this case with a percentage difference of 1.15% (cf. with d-orbitals 2.30%). They are both however a good match to the found expeimental values.

Last looking at the P-Mo-P angles there is seen to be a difference between the literature values and calculated (2.30%) but when the d-orbitals are included the error is reduced to 0.91%. These are again however both a good match but the match is better when the d-orbitals are included.

Now looking at the trans complex (remembering that it is not the exact complex in literature). The Mo-P bonds are in good agreement. Initially they are too long but then once the d-orbtials are introduced the bonds are tightened and agree well with the literature. The percentage differences are: no d-orbtials=2.87% d-orbitals=1.00%.

In the case of the C-Mo bonds including the d-orbtials makes the calculated distances worse. However in each case the match is extremely good. Without the d-orbtials the percentage difference is 0.88% and with the d-orbitals is 0.95%. This small sacrifice of this length is definitely outweighed by the vast improvement of the Mo-P bonds above.

Looking at the P-Mo-P angle the inclusion of the d-orbitals has again slightly hindered the accuracy of the angle. However this increased error is again really small and not worth mentioning really. The angle is really a very good match in each case. The percentage difference is 0.59% and 1.09% respectively (both good matches)

Overall this has shown in the cis and trans -isomer cases including d-orbtials into the calculations are overall beneifical to the geometry. In both cases however the modelling is accurate to the literature values with no large dicretions and shows the accuracy of computational modelling in this case. Also when looking at the percentage difference between the literature and calculated parameters in the both the cis and trans case they have both been modelled to roughly the same accuracy (i.e.neither isomer is really better modelled than the other).

The next thing that can be analysed is the IR spectrum of the molecules. Specifically the CO region is looked at because this is the most interesting and important region of the spectrum. The calculated values will be compared to literature findings as to assess the accuracy. The effect of including the d-orbtials in the calculation will also be assessed in terms of the frequency (as oppose to in the geometry above).

The literature values for the frequencies:

Carbonyl Stretching Frequency/cm-1
Cis	Trans
2019	1895
1922	-
1905	-
1899	-

Notice that there is only one IR active stretch for the trans complex and the significance of this will be discussed later on.

Now comparing these to the calculated frequencies. The trans isomer will be looked at initially. At the beginning of each of the following paragraphs firstly the literature value for the CO frequency is quoted, then corresponding calculated non-d-orbitals figure and then the d-orbtials figure. Also the symmetry of the stretches (as discissed afterwards) are included:

Frequency 1: 2019, 1960.07, 1959.65 (symmetry A₁)

Frequency 2: 1922, 1869.45, 1873.2 (symmetry A₁)

Frequency 3: 1905, 1850.29, 1854.59 (symmetry B₁)

Frequency 4: 1899, 1848, 1851.03 (symmetry B₂)

Looking at these frequencies it can be plainly seen that all the calculated frequencies are lower than the measured experimental values. The stretches are weaker which implies that the bond are not strong enough to match with the expected frequencies. Including the d-orbtials in most cases and has helped in increasing the frequency but only by a small amount in each case and does not bring the frequencies up to the desired level. In the highest CO frequency case including the d-orbtials has lead to a small decrease but really one could say has really made no difference.

Overall in terms of frequency accuracy this method has not lead to highly accurate results. The error in each case seems fairly systematic with a difference of ~50cm^-1 each time. Overall however given the complexity of the system and it's bonding it really is not a bad prediction at all.

Now to look at the accuracy of the frequencies calculated in the cis isomer (note: IR inactive stretches can't be compared as no literature exists)

Frequency 1: 1895, (1838.86/1838.97), (1843.9/1844) (symmetry E_u)

In this case there is only one CO frequency compared to the 4 above. There are two frequencies in the calculations in the calculations but they are basically the same and the only reason there are two is because the modelled molecule is not of prefect symmetry. Again including the d-orbtials increases the frequency of the CO stretch and brings it more inline with the literature frequency. The error in this case is about the same as before at around 50cm^-1. Again showing that the programme can make a good prediction of the stretching frequency of this complex system to a fairly accurate level.

Another thing to consider is the number of these CO stretches in each case.

In the cis complex there are bands in this region. This is characteristic in cis-complexes (pseudo-C_2v) of this type due to their point group The trans complex however has only the one band present because of its symmetry (pseudo-D_4h). The reason for this change in number of CO strecthing bands is because the symmetry change changes the number of IR active stretches.

If CO ligands are not related by a centre of inversion (i) then N CO ligands will produce N IR bands . In this case 4 COs produce 4 bands. If however there is a centre of symmetry some bands will not be IR active as there will be no change in dipole moment during the stretch. E.g. if all COs go in and out from the metal centre simultaneously (symmetrically) then there will be no change in dipole and so this mode will not be IR active. This amounts ultimately to there being only one CO band (as seen above) in the IR spectrum of the trans(psuedo-D₄h)complex. In order to see these stretches which are not present in IR spectra Raman spectroscopy can be used.

Ultimately the irreducible representations of the IR active stretches seen for pseudo-C_2v complexes are Γ_irr=2A₁+B₁+B₂ (as labelled above) For D_4h stretches include Γ_irr=A_1g+B_1g and E_u. However the only IR active mode, as discussed previously a change of dipole is required, is the E_u mode which is why only the one band is observed. In terms of labelling the symmetry of the inactive stretches the A_1g strech is the highest CO frequency stretch and the B_1g is the next lowest.

If the symmetry is not perfect (as in this case) the technically inactive IR groups can show up in the spectrum feintly (as seen in the calculation) but they are likely to be so weak they would still not be seen on a true spectrum.

The results of all this can be seen in the computed IT spectra for the two isomers. Since the spectra are really similar with and without d-orbitals only spectra with the d-orbitals will be be shown below:

Note also that at the following DOIs the optimised structure information (for the with d-orbtials structures) can be found

IR-Trans isomer DOI:10042/to-1052

IR-Cis isomer DOI:10042/to-1053

One can then compare the energies of the complexes in their cis/trans form. This can be done including and excluding d-orbitals. The analysis can be seen below:

no d-orbitals:

trans= -773.35731311 Hartree

cis= -773.36024008 Hartree

Thus the cis is more stable by: 0.002927 Hartree = 7.685kJmol^-1

including d-orbtials

trans= -773.43967737 Hartree

cis= -773.43857579 Hartree

Thus the trans isomer is more stable by: 0.001102 Hartree = 2.892 kJmol^-1

This shows that it makes a difference whether or not d-orbitals are included in the calculation on which isomer is the most stable. Literature says that trans is the most thermodynamically stable isomer. Thus this shows in order for the calculated results to match up with experiment the d-orbitals must be included. This again shows the importance of including this factor in the calculations.

In order to tune this preference steric bulk could be altered on the ligands. Also the electronic properties could also be altered. More steric demand would favour the ligand to be furthur apart (i.e using triphenylphosphine rather thantrimethyl phosphine would likely increase the preference of the trans complex). Electronically altering the ligads could potentially change this order. It has already been shown that the d-orbtial contibution can change the preference; of course in real life the d-orbitals can't be switched off as such but altering the substituents (EWG/EDG) will most likely change the orbital distribution such that the isomeric preference is changed.

Values for the energy difference between the cis and trans bispyridine-tetracarbonyl molybdenum complex (Arun Shivalingam) is calculated to be 50.85703771kJmol^-1 but this time in favour of the cis complex.

So is there a reason why in the Phosphine case there is a preference for trans and in the case of pipreridine there is a preference for cis?

In the both cases studied I don't believe sterics of the ligand (trimethylphosphine/pyridine) is large enough to dictate the trans ligand should be lower in energy so I think the reasoning should come from more complex electronics of the molecule. Ignoring the d-orbitals in the trimethylphosphine case leads to the cis isomer being the most stable as in the pyridine case. One might think the cis isomer (being of lower pseudo symmetry C_2v) would maybe be lower in energy as there is more potential for mixing (and hence lowering in energy)of occupied orbitals so this makes sense. In both cases the ligands aren't very good pi-acceptor (ignoring d-orbitals of P) and thus the cis isomers are the most stable. As soon as good pi-accepting ability is given to the phosphorous (now strong field) by adding d-orbitals the preference of the cis-trans order flips. Thus the pi-donating/pi-accepting ability of the ligand likely effects the preference (backing up the above statement about how one might go about adjusting cis-trans energy order). This trend would be better represented with a larger field of trialed ligands, however it seems to make sense. There is likely to be some stabilising force that arises by having the two pi-accepting ligands trans to each other accepting electron density.

Day 3

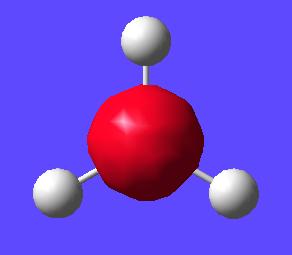
In this part of the experiment ammonia will be studied. The first thing that is done is to optimise the molecule (NH₃) in gaussview using gaussian. This is done using the B3LYP method and 6-31G basis set. The 6-31G basis set is more advanced than simply the 3-21G basis set. "X (the first number in X-YZg) represents the number of primitive Gaussians comprising each core atomic orbital basis function". Having more functions increases the accuracy of the calculation. The script used to run this calculation is:

"# opt b3lyp/6-31g"

Here is an image of the summary of the calculation:

Note: The symmetry of the molecule is in fact C_3v as expected (found in results-->summary)

The next step is to form a molecule of ammonia and then to change one of the inital bond lengths to 1.01angstroms using the modify bond tool. This then made the point group change from C_3v to C₁. The optimisation calculation was then ran but this time ignoring the symmetry of the molecule. The script used to do this is:

"# opt b3lyp/6-31g nosymm"

Here is the output summary of the molecule:

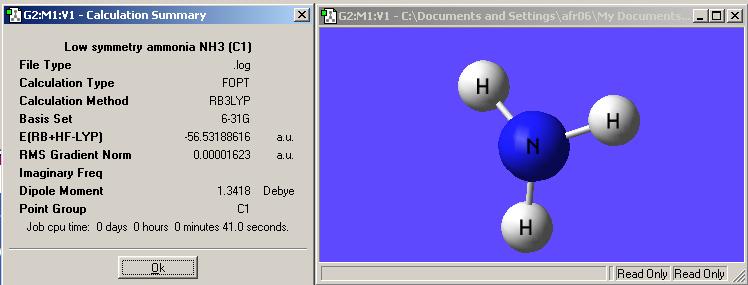
It can be seen that in ignoring the symmetry in the input leads to the output retaining the C₁ symmetry.

The next thing to do is to try and investigate the possible D_3h symmetry of ammonia as the hydrogens and nitrogen become planar. In order to do this a dummy atom must be introduced into the set-up as to help define the restricted symmetry. Then an optimisation calculation was ran at the same 6-31G level as before. This was initially done as 3-21g (Hartree-Fock) because this was the script uploaded on the website. Both have been put into this report just as a point of interest to see what the difference between the answers the two methods give. Here are the two summaries. First is the 3-21g version and secondly the 6-31g:

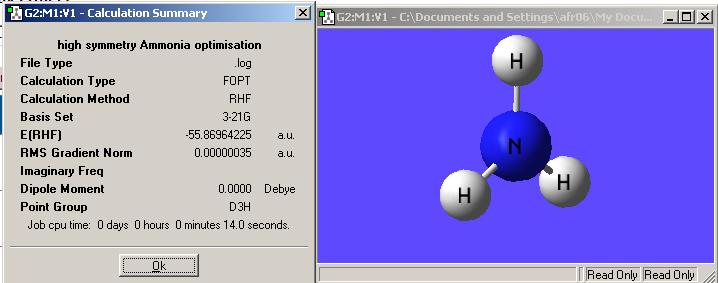
There is an energy diffference between the two difference optimisatons of 0.662 Hartree=1737.82kJmol^-1. This is a signficant energy difference and shows that it is important which basis set and method is used to run a calculation. The higher level 6-31g calculation is a better approximation than the 3-21g because the first peak in the radial distribution function is modelled by 6 gaussians rather than 3.

Now the information for 6-31g has been gathered the findings can be analysed. The optimisation curves can be found easily by opening the file with intermediate geometryies read and then going to Results--->optimisation

Here is important geometrical information found during these optimisations:

6-31g optimisations	C3v	C1	D3h
Bond Length/angstroms	1.00580	1.00596 x2, 1.00597	1.00037
Bond angles/degrees	116.185	116.137 x2, 116.143	120
Jmol
Optimisation Curves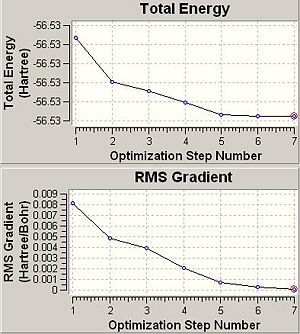

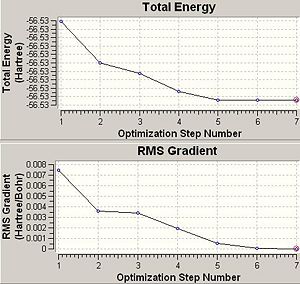
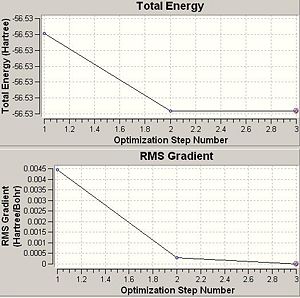
So does the symmetry of the molecule make a difference to the final structure obtained in anyway. There is an obvious difference in structure between the planar D_3h and other two point groups as one might expect. The difference however between the other two point groups however is only very small as can be seen by looking at the bond lengths and angles above. The energy difference between these two C_3v and C₁ point groupsis only very small at 2.88895 kJmol^-1. This is because they are very similar in structure and so would expect the energies to be similar.

The C₁ point group in ammonia is slightly lower in energy than the C_3v point group because of the higher conformational freedom the calculation that is run has. When an optimisation calculation is run the symmetry of the molecule is maintained unless specified to be ignored (this can be done by ticking the "ignore symmetry" box under calculate-->Gaussian-->general i.e. a molecule can be allowed to "break symmetry" during an optimisation). Thus giving more conformational freedom allows a lower energy to be found.

Another important factor to consider is the time of the calculation. Since there are more conformational possiblilites for lower symmetry systems this also means there are more to be explored during an optimisation and this then means the calculation will take a longer time to run. This can be seen in the optimisation times seen in this section above. The highest symmetry D_3h takes 16.0 seconds to run. The lower symmetry C_3v takes longer at 36.0 seconds and the lowest symmetry C₁ ammonia takes a longer 41.0seconds to run. This is also evident in the graphs above that show optimisation steps vs. energy. The D_3h takes only 3steps to optimise whereas the others take 7 steps each to optimise.

Thus defining a higher symmetry to a molecule means the calculation time is reduced. In this case the difference between C_3v and C₁ energies and geometries is so small that it is worth maintaining the C_3v symmetry to reduce the time of calculation for a small sacrifice in the energies and geometries. This effect is exaggerated in large molecules where defining the symmetry would lead to large reduction in computational time that will only marginally effect the answers. So overall a high symmetry conformation of a molecule will optimise in a shorter time than a lower symmetry one.

The difference between the highest and lowest energy geometries in this case is:

ΔE=E(D_3h)-E(C₁)=-56.53154189-(-56.53188616)= 0.00034427 Hartree= 0.904 kJmol^-1.

If one compares this to the thermal energy at room temperature (RT=2.478kJmol^-1) it is significantly smaller and shows that ammonia can get from the C₁ (roughly C_3v) to D_3h conformations at room temperature. This will be looked at again soon when considering higher level calculations.

Beyond what has already been done the above the modelling can be furthur improved using an even better basis set and method. The method that will be used is MP2 and the basis set is 6-311g+(d,p). This method was also run to include all electrons, by ticking the "include all electrons" box in the method options in gaussview. This is run on both the C_3v and D_3h symmetries of ammonia. The script used in order to run these calculation was then:

"# opt mp2=full/6-311+g(d,p) geom=connectivity"

The result summaries for these molecules can be seen below:

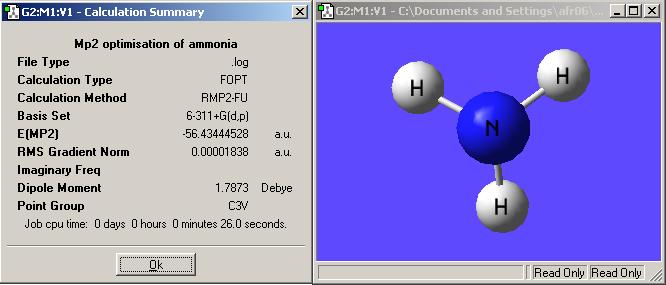
These calculations do take longer than the former more simple calculations by about 10seconds. This is however only a simple molecule and increasing the number of atoms by only a small amount could increase the calculation time dramatically. In this case the energies are different enough from the more simple calculations to make it seem worth while to carry them out.

The energy difference between the two different conformations of ammonia is:

MP2/6-311+G(d,p)

ΔE=E(D_3h)-E(C_3v)= -56.42664911-(-56.43444528)= 7.79617x10^-3 Hartrees= 20.468kJmol^-1

B3LYP/6-31G

ΔE=E(D_3h)-E(C_3v)= -56.53188605-(-56.53154189)= 3.4416x10^-4 Hartrees=0.9036kJmol^-1

It can be seen that the energy difference between the two isomers is actually quite different in the two methods. Using the more advanced MP2 level of calculation the energy differece is actually 23 times larger than in the cruder B3LYP method. The more advanced method however is definitely worth running in this case because the energy difference between the two conformers matches very close with the experimental value of 24.3 kJmol^-1. The percentage difference is only 15.7% which is good. Using this level of calculation can be shown in this simple case to give a very close answer to experiment. Given the result from the 6-31g is far off it is important than the higher level MP2 method is ran to get an accurate result in this case. The reason why MP2 gets a far more accurate answer in this case is that it takes highly into account the dynamic correlation of electrons. The B3LYP method does take this into account (unlike the Hartree-Fock method) but nowhere near to the saem level as in MP2.

When looking at this energy of 24.3 kJmol^-1 and now comparing it to thermal energy at room temperature (2.478kJmol^-1) it is now higher (at the lower level B3LYP the energy barrier was only 0.904 kJmol^-1). This means that although conversion at room temperature will occur it will happen a lot less readily than the lower energy calculation would have one believe. An explanation to why interconversion does occur at room temperature could be(classically): although thermal energy is lower than the barrier one must remember there will be a boltzmann distribution and some molecules will have the energy to invert. Given this energy difference is not really, on the grand scale of things that large, a large enough proportion of ammonia molecules will have the energy to interconvert at any one time to make interconversion prevelent throughout all the molecules.

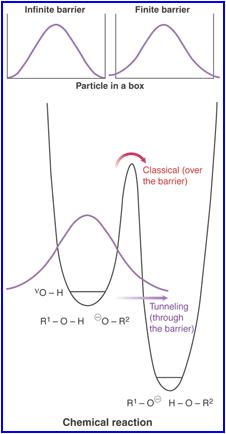
Even with this explanation it would explain why interconversion occurs but would not explain why it still happens so readily. The reason for the ready interconversion of ammonia is actually thought to be due to quantum tunneling. Thus in order to get from one C_3v molecule to the other the energy barrier doesn't acutally need to be overcome. Tunneling of ammonia in this way can be used in a MASER (Microwave amplification by stimulated emission of radiation) . The rate of quantum mechanical tunnelling depends upon mass of particles, height of barrier, width of barrier and dissipation. Increasing the first three factors decreases the tunneling rate exponentially. The dissipation can reduce tunneling also and can acutally make it 0 . Tunneling also has no dependance on room temperature to a first approximation whereas in classical there is a very strong temperature dependance. The dependance however of tunneling on barrier-width can lead to a "dependance" as such on temperature. Thermalpopulation of higher enerngy vibrational levels may help promote tunneling because barrier width decreases as one moves up the potential energy well. Also if reacting centres are brought close together due to large conformational movement tunneling can also be promoted.. Tunneling can be seen in this diagrammatic representation below (it is not ammonia tunneling but it gets the idea across well:

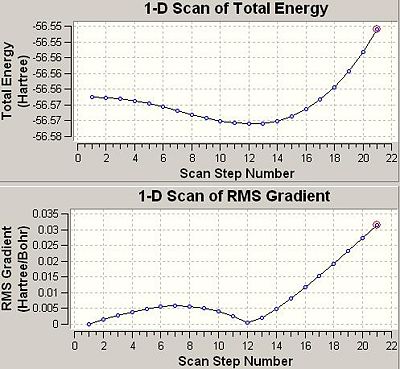
Next the inversion path of ammonia can be followed. This is done by submitting a "scan". In this method one coordinate is moved whilst the others are allowed to optimise. Since the input file that is needed is more complex than the understanding of the course. Thus the .txt file is simply extracted from the course instructions and saved. The file extension was then changed to .log file and opened in gaussview with the "read intermediate geometries" option checked.

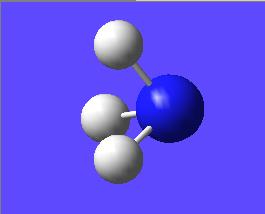
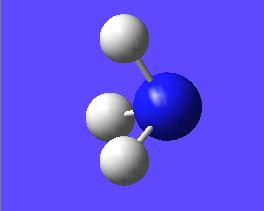
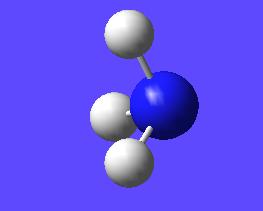
This "umbrella motion" can be represented in series of snapshots as seen below (every 3rd optimisation intermediate is shown):

"Umbrella motion" of Ammonia

Profile of total energy of Scan

The final part of looking at ammonia in this experiment us to examine the frequencies in both the C_3v and D_3h symmetries. This will be done in each case by looking at the B3LYP/6-31g level optimisation calculations of both molecules.

These are calculated by simply loading the previously optimised structures and then running an frequency calculation on them. The script used to run this calculation is:

"# freq b3lyp/6-31g geom=connectivity"

The frequencies for both molecules when the calculations are run in this way can be seen below:

C3v		D3h
Frequency/cm-1	Intensity	Frequency/cm-1	Intensity
456.262	595.862	-318.051	849.113
1680.73	41.541	1640.59	55.9828
1680.73	41.5398	1640.59	55.9805
3576.87	0.0644	3635.71	0
3576.97	6.9468	3854.27	19.5951
3776.98	6.946	3854.27	19.5963

An interesting point to note about this is that if one goes to results-->summary the symmetry of the molecules has changed. In the C_3v case the symmetry has changed to C₃. In the D_3h case the symmetry has changed to C_3h. Just to see if these symmetry changes have made any difference to the output frequencies the calculations were run again but with the symmetries predefined in gaussview. This is done by going Edit-->Point group--> Check "Enable point group symmetry"-->select appropriate point group from the "constrain to subgroup" drop down menu.

Here are the results of the frequency calculations with this change:

C3v constrained		D3h constrained
Frequency/cm-1	Intensity	Frequency/cm-1	Intensity
456.261	595.862	-318.051	849.113
1680.73	41.541	1640.59	55.9828
1680.73	41.5398	1640.59	55.9805
3576.87	0.0644	3635.71	0
3576.98	6.9468	3854.27	19.5951
3776.98	6.9461	3854.27	19.5963

This shows that contraining the symmetry really makes no difference and so this breaking of the point groups that occured on the first frequency calculation must have been really small and hence has really made no difference to the frequency. this is as expected but it is better to confirm that this is the case.

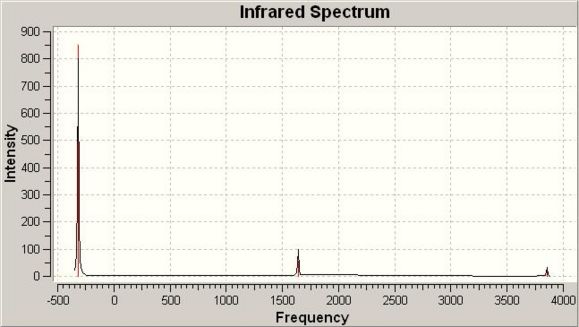
Notice that the D_3h symmetry ammonia has one negative frequency. This is characteristic of a transition state. All other frequencies are positive. The C_3v case has no negative frequency.

An important point to notice is which frequency in which conformation follows the reaction path as seen in the previous scan experiment. This is the negative frequency stretch at -318.051cm^-1 in D_3h which goes from one ammonia umbrella shape to the other through the flat transition state structure. In C_3v the vibration that follows the inversion path is also the first vibration but this time the frequency is at 456.261cm^-1 (positive).

An interesting point to note about this part of the experiment is the phenomena which occurs to break the Born-Oppenheimer approximation and to cause a second order Jahn-Teller distortion (non-degenerate orbital mixing). In the D_3h ammonia orbital mixing can't occur (only orbitals of the same symmetry can mix). When the molecule is put into a vibration the point group is then broken in its symmetry and the orbitals that could not mix now can (second order Jahn-Teller distortion). The fact that the vibrations have an effect on the electronic structure of the molecule is a break down of the Born-oppenheimer approximation in which electronic structure and vibrations (as well as other rotational and translational motion) can be considered seperately. This orbital mixing effect is why the C_3v is prefered over the D_3h ammonia conformation.

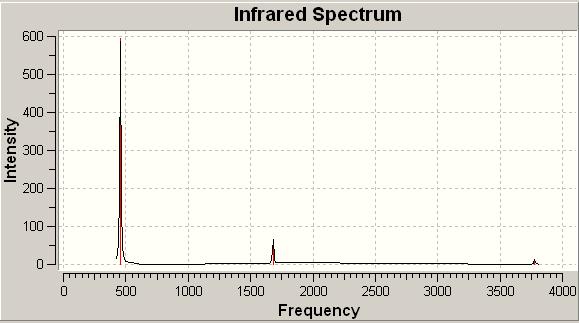
In almost all cases the literature frequencies (labelled in the table below the IR spectra to follow) and computed values match up well. However one frequency is along way off of the literature at 456.262 rather than 968. The reason for this is that the calculation has broken down because quantum effects must be taken into account for the frequency to be calculated correctly and in this case they are not.

The IR spectra of the two conformations can be seen below:

IR spectrum of C_3v

IR spectrum of D_3h

One can then compare and contrast the frequencies of both of the conformations. Since C_3v is a sub-set of D_3h equivalent vibrations can actually be found in each case. This can be seen summarised below:

D3h vibrations				C3v vibrations
Frequency/cm-1	Intensity	Form	Symmetry assignment	Frequency/cm-1	Intensity	Form	Symmetry assignment
-318.051 (wagging)	849.113		A"2	456.262 (wagging) (lit 968)	595.862		A1
1640.59 (HNH scissoring)	55.9828		E'	1680.73 (HNH scissoring/rocking) (lit 1626)	41.541		E
1640.59 (HNH scissoring/rocking)	55.9805		E'	1680.73 (HNH scissoring/rocking) (lit 1626)	41.5398		E
3635.71 (NH symmetric strectching)	0		A'1	3576.87 (NH symmetric stretching) (lit 3337)	0.0644		A1
3854.27 (NH asymmetric stretching)	19.5951		E'	3776.98 (NH asymmetric stretching) (lit 3444)	6.946		E
3854.27 (NH asymmetric stretching)	19.5963		E'	3776.97 (NH asymmetric stretching/symmetric stretching) (lit 3444)	6.9468		E

Mini Project-Borane structures

In this mini-project boranes and specfiically borane clusters will be investigated into. Firstly the general electronic structures of some closo boranes will be looked at. Next specific types of carboranes and their function as superacids will be investigated. The last thing that will be looked at is a specific reaction of a closo-borane and the electronic structure of the product of the reaction.

The inital molecule that is going to be investigated is the Closo-B₆H₆^2-. This was drawn in Chembio3D, saved as a .gjf and then opened in gaussview. The molecule was initally drawn such that it was in an octahedral geometry as predicted by Wade's rules. Then a DFT, B3LYP, 6-31(d,p) optimisation and frequency calculation was run on the molecule. The molecule also had a 2- charge added to it. This was done by editing the script in the following way (note the -2 just above the atomic co-ordinates specifying a charge and the pop=full for a full MO analysis):

# opt freq b3lyp/6-31g(d,p) pop=full

 b2h6opt_freq dft 6-21g

 -2 1
 B                 -3.86600700    1.16137100   -1.34015600
 etc...

The resulting molecule co-ordinates can be seen below:

Closo-B₆H₆^2- DOI:10042/to-1054

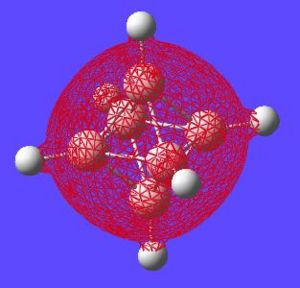
The next thing that is interesting to look at is the generated MO's of the molecule. Closo-boranes tend to be very unreactive compared to other types of boron cluster (nido-, arachno-). This stability has been suggested to be linked to "3-dimensional aromaticity". The MO diagram of this cluster can be looked at in order to try and justify such an aromatic type system.

Aromaticity is an extra stabilisation recognised in a molecule that is not accounted for conjugation alone and can be thought of as a cylic delocalisation of electrons.. Thus if in a molecular orbital there looks to be a possibility of this kind of cyclic (or spherical in three dimensions) delocalisation of electrons this could lead to aromaticityin the molecule. After opening and looking through the molecular orbitals of this struture these are the orbitals that look like they could help lead to aromaticity:

Here are the molecular orbitals that look like they should give rise to some sort of aromatic stability:

Note: the orbitals calculated can be imagined with a smaller isovalue such that some lobes that wouldnt usually meet, would meet due to the "increase in size" of the orbitals boundary surface

Potential Aromatic MOs of Closo-B6H62-

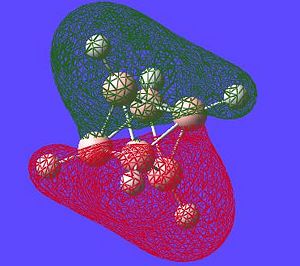
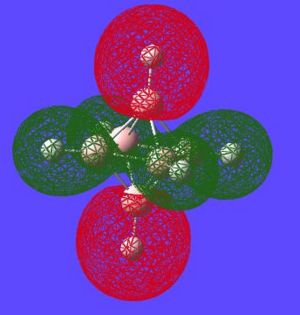
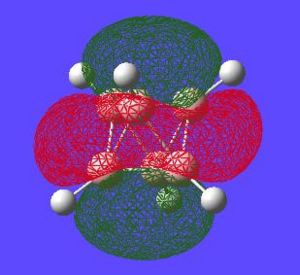
Another interesting point to make is that all occupied orbtials are bonding in the case of this cluster and no antibonding are occupied. This is just like a benzene type arrangement where all the occupied orbitals lie below the non-bonding level. Looking at the evidence the 3D aromaticity of Closo-B₆H₆^2- seems likely.

Now to look at the potential superacidic properties of related carborane species. Taking the closo-B₁₂H₁₂^2- borane cluster and replacing one of the boranes with a carbon (and then reducing the overall charge to -1 to maintain the closo structure), and replacing all boron hydrogens with chlorine results in the conjugate base (anion) of a superacid (H(CHB₁₁Cl₁₁). This superacid is one million times stronger than sulphuric acid and can be used to protonate C₆₀ without damaging or decomposing it. In order for this to be a strong acid the conjugate carbonane anion must be highly stable. This might be expected given the 3D aromatic nature of borane/carborane clusters that would help delocalise the charge slightly. Also electronegative substituents can be used to aid the stability of the resulting anion.

In order to study this stability an acid base reaction scheme will be studied. This reaction scheme that will be used is:

H(CHB₁₁Cl₁₁) + H₂O --> (CHB₁₁Cl₁₁)^-1 + H₃O⁺

So protons will be used as the acid of carborane base (in reality a variety of Lewis acids can be used) and since a proton can't be modelled electronically (no electrons) water and the hydronium are introduced into the reaction scheme.

Water and hydronium are modelled at the same level as the carborane anion base and the protonated carbonane acid. This resulted in energies for the two species of:

H₂O = -76.41431631 Hartree

H₃O⁺ = -76.70417459 Hartree

So the energy gain from protonating water is 761.02 kJmol^-1

The superacid will also be modified in order to see if the acidity of the superacid can be changed. This will be done by changing the EWG groups attached to the acid and by changing the number of EWG groups attached. The electronegative Cl atoms will be changed to F and Br and the effect will be noted. Also the structure will be tested with only 1, 2 and 3 Chlorines attached and seeing how the acidity is effected by this. In order to run the calculations (optimisation, frequency) in the cases where the types of atoms will be changed the Lanl2dz basis set will be used with the b3lyp DFT method. The Lanl2dz method is used to account for the heavier atoms in some of the structures (e.g. Br) by using pseudopotentials for the non-valence electrons. Obviously if this method/basis set if used for the heavier elements (Br) for fair comparison to idenfify a trend it must also be used when only first row (F), and first and second row (Cl) elements are present also. When looking at changing the number of electronegative elements only Chlorine (nothing heavier) is used and so the 6-31g(d,p) basis set will be used to run the calculations. Note also it is important to ensure the charge is correct in each case (-1 for anion and 0 for protonated species). This can be done directly in gaussview under calculate-->gaussian-->method-->charge or can be done by directly editing the script. In the script below the -1 refers to the charge and the 1 to the multiplicity (singlet state).

# opt freq b3lyp/6-31g(d,p) pop=full

[No Title]

-1 1
 B                 -2.44622600   -0.19667600   -0.09126900
 B                 -3.37917500    0.16858900    1.28593600
 B                 -4.88760500   -0.60752500    1.12206200

Here is the script used for the "changing atom type" calculations:

# opt freq b3lyp/lanl2dz pop=full

Here is the script used for the "changing number of substituents" calculations:

# opt freq b3lyp/6-31g(d,p) pop=full

Another thing that must be considered is the site of protonation of the carbanion in the protonated version (i.e. where would it protonate if it had to?). In order to do this the optimised standard (i.e. all borons with chlorines attached) superacid was run through an NBO charge analysis. This is run using the following:

# rb3lyp/lanl2dz pop=nbo geom=connectivity 

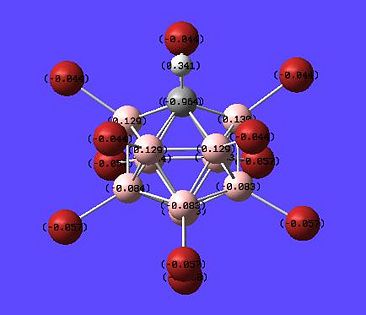
Once the calculation was run and the output file opened the charges were displayed by going Results-->Charges--> and then selecting NBO from the "charge type" drop down menu. Here is the result of this calculation with numerical values and with a "colour by charge" scheme (see image for colour-to-charge spectrum):

Chlorinated NBO DOI:10042/to-1073

Charge Distribution on Superacid's conjugate base

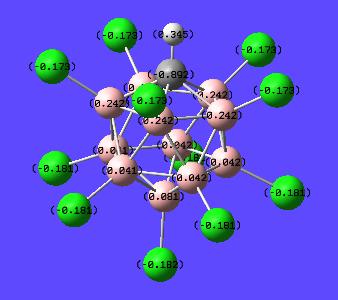
This has shown that the excess extra electron is found mainly on the carbon (-0.892). However the chlorines also help stabilise this extra charge (-0.173 and -0.181). It is expected that the carbon would have this extra charge situated mainly on it since it is group 4 rather than group 3 (Boron). This then means if one was to protonate (or add a lewis acid to) the structure it would be expected to sit on this excess negative charge. Thus the proton was placed onto the carbon alongside the other hydrogen and the optimisation-frequency calculations run again in each case.

Here are the resultant found structures for the superacids and there conjugate base: Order: Fully Chlorinated, Fully Fluorinated, Fully Brominated, Singly Chlorinated, Doubly Chlorinated, Triply Chlorinated

Superacids optimised structures
Superacids
Coresponding carbanion

Anion Publications (In order of left to right): Unable to publish,DOI:10042/to-1077 , Unable to publish,DOI:10042/to-1078 ,DOI:10042/to-1079 ,DOI:10042/to-1080 .

Superacid (In order of left to right): DOI:10042/to-1076 , Unable to publish, Unable to publish,DOI:10042/to-1074 ,DOI:10042/to-1075 , Unable to Publish.

Here are the energy results for the carborane anions (second energy) as well as their protonated counterparts (first energy):

all fluorine: -1411.47931514 -1411.18417848 difference=0.29513666 Hartree= 774.8813 kJmol^-1 overall reaction change: 13.8584kJmol^-1

all chlorine: -477.38454386 -477.09255566 difference=0.2919882Hartree= 766.6150 kJmol^-1 overall reactio change: 5.5921kJmol^-1

all bromine: -457.74642850 -457.43741447 difference=0.30901403Hartree= 811.3163 kJmol^-1 overall reaction change: 50.2934kJmol^-1

1 chlorine: -779.01767504 -778.64912229 difference=0.36855275Hartree= 967.6352 kJmol^-1 overall reaction change: 206.6152kJmol^-1

2 chlorine: -1238.2905830 -1238.65631532 difference=0.36573232Hartree= 960.2302 kJmol^-1 overall reaction: 199.21kKmol^-1

3 chlorine: -1698.2908 -1697.924055 difference=0.366745Hartree= 962.8890 kJmol^-1 overall reaction change of 201.8690kJmol^-1.

These results are extremely good and some analysis can now be done on the numbers. The most acidic molecule when modifying the different atoms attached is that with all chlorines attached. One might expect that the flourinated acid would be the most stable because of the fact it is the most electronegative and would help stabilise the anion chrage the best on deprotonation. This is however not the case. The superacid is least acidic following the electronegativity trend (least electronegative least help in stabilising charge and so least acidic). In order to help confirm that one would expect F to help stabilise the charge best NBO charge calculations are run on the two remaining molecules (Br and F). If indeed the F should stabilise the charge the best there must be another effect thst is causing it to be the least acidic of the set.

The absolute values of these reaction energies can be interpreted by comparing to the thermal energy available at room temperature (298.15K). Energy available=RT=2.45kJmol^-1. Thus given the energy in the calculations can be up to 5kJmol^-1 out the energies for the flourine could be quite low also. Including this energy error in the Cl case the energy could be well under this thermal energy (could even be below 0) and would explain the high acidity. For the bromine case the reaction energy would still be very high even considering this error and so wouldn;t be expected to be a very good acid compared to the other two. Another good comparison to make is to a hydrogen bond. A hydrogen bond is consdiered a weak interaction with energies varying from around 5-30kJmol^-1. A weak covalent bond is also around 155kJmol^-1 and a normal C-H bond around 413kJmol^-1 . Thus this loss of a proton process is alot weaker than even in a "weak" hydrogen bond. Thus the fully chlorinated superacids acidity can be compared to something tangible and can be recognised for the strong acid it is using computational methods.

All this is of course assuming a thermodynamic arguement. In order to get kinetic information out the transition states would have to be studied. One might expect, roughly, using hammonds postulate that the most important factor in stanilising the transition state is the charge stabilisation but this would have to properly studied to be conclusive.

In terms of varying the number of chlorines attached the trend is generally as expected. Clearly having only 1-3 chlorines attached has caused it to be far less acidic than when all Borons have chlorines on with an overall energy of reaction of 206.6152kJmol^-1 (cf. 5.5921kJmol^-1). However increasing the number of chlorines does increase the acidity of the superacid as expected generally; more electronegative elements help stabilise the charge of the anion and so increase the acidity of the superacid. However just over the ran 1Cl, 2Cl and 3Cl experiments although going from 1 to 3 chlorines the acidity increases but going from 1-2 it decreases. In fact having just two Chlorines is the most acidic of the three situations. The errors of the calculated energies is likely to be enough such that the energies overlap and so increasing number of chlorine does increase the acidity and the error of the experiment leads one to believe otherwise OR On a large scale trend adding chlorines does increase the acidity of the superacid but over the range of a 1 chlorine increase subtle orbital effects may not mean there is always an increase on adding each carbon.

So lets look at the results of the NBO analysis of the F and Br substituted superacids and see of any light can be shone on the above results.

Fluorinated superacid NBO DOI:10042/to-1072

Brominated superacid NBO DOI:10042/to-1071

Fluorinated Superacid	Brominated Superacid

The results do not really open out the results particularly but give rise to some ideas that might explain the trends observed. The electron density on the electron rich carbon does infact decrease with increasing electronegativity of the elements (F=-0.812,Cl=-0.892, Br=-0.964) which does help explain why the Br acid is going to be the worse acid. It doesn't explain however why the fluorine superacid is the worse acid. In order to determine the true reason for the difference in acidity in the fluorinated superacid more advanced analysis is likely to be required. No analysis done reveals the reasons for this. Fluorine is a strange element with usually anomalous properties due to its high electronegativity. The reason for the difference is going to be down to some orbital effect but this has not been identified in this case. It again worth noting the effect is likely to be subtle given that firstly there is error in the energy associated with the calculation and secondly the energy differnece is only small anyway to the chlorinated species compared to that of the fully brominated case which is way up at 50.2934 kJmol^-1.

Another thing that is interesting to look at is the calculated ¹¹B NMR for the calculated fully chlorinated superacid. Here is the spectrum:

Boron NMR of Fully Chlorinated superacid (Unable to publish to D-space)

The important thing to take from this NMR is the fact that the general paettern matches what one would expect in a 1:5:5 ratio. This is an important technique in classification of carborane type compounds. In 1967 ¹¹B NMR was used in order to prove the structure of the related carborane B₁₁CH₁₂^2- . The fact that the peaks can be found in the 1:5:5 ratios proves that the C adopts an apical poistion. The apical boron directly opposite has the lowest chemical shift at -10.7871ppm(reference: B2H6 HF/6-31G(d) GIAO). The next closet five borons are at around -17.76ppm and then then five closest borons are found at around -20.41ppm. This means the closer to the carbon the more shielded appears to be on the borons. There will, i'm sure, be some aromatic type influence on the shifts also due to ring currents but this would require a lot furthur work to determine.

The next thing that is going to be looked at briefly out of interest is the reaction of carboryne with a alkyne in a Diels-Alder type reaction :

Carborynes reaction with alkyne <ref="DA">Carboranes-Wikipedia Carborane</ref>

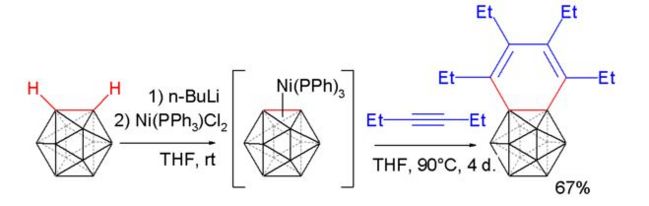
The interesting point about the product is that the potential benzene ring type structure (benzocarborane) actually shows no aromatic type structure over the benzene-type ring itself. The structure was optimised and an MO analysis run on it (pop=full) at the lanl2dz level.

# opt freq b3lyp/lanl2dz geom=connectivity pop=full

The bond lengths around the ring indeed suggest that the ring is not fully electron delocalised symmetrically (as in benzene's D_6h symmetry type delocalisation) due to the variety of bond lengths around the system. These can be measured on the output to be 1.66, 1.50, 1.37 and 1.49 angstoms (going from the bnod included in the cluster to the furthest away single C-Cbond). These agree with the literature X-ray values fairly well of 164.8 pm to 133.8 pm. This shows the calculation run is actually very accurate.

The structure optimised structure can seen below DOI:10042/to-1096 :

All of the MOs for this molecule where generated and examinated looking for orbitals on the benzene ring which would make it look aromatic in a symmetric way about the whole molecule. However these could not be found as expected. Given two of the carbons are encorporated into the carborane structure it is not expected that the benzene type delocalisation will be seen. i.e. boron based orbitals will interact with encorporated carbons breaking the symmetry of the "bezene-type" ring structure. There are however a few interesting orbitals which can be seen with analysis below:

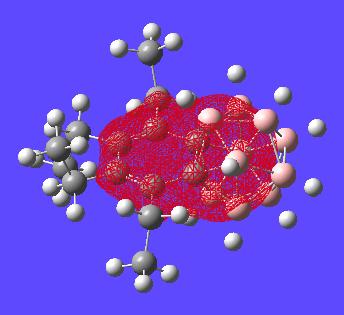
This MO shows both the carborane cluster and the "benzene" ring encorporated in the same orbital. this may suggect delocalisation of the electrons of the whole structure (two aromatic systems).

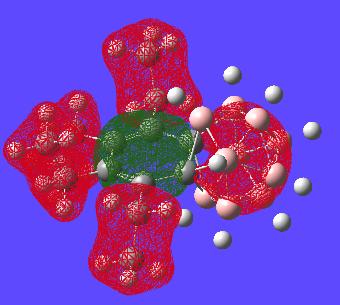
This orbital is the only orbital that looks the most like it has part of an orbital all in phase that only resides in a cyclic fashion on the benzene ring. This might suggest the bond lengths should really be alot closer in size to each other but clearly nearly all other MOs do not involve this type of delocalisation over the benzene and hence why the benzene ring has difference bond lengths.

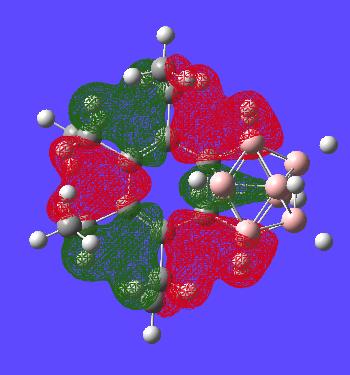
This MO is simply to show the that the benzene ring is generally symmetric as in normal benzene until the carborance cluster interferes with the orbitals as expected. The one (green) carborane based orbital is alot smaller than the other ones (again showing the lack of symmetry in the ring)

This part of the project really has no conclusion to draw other than that the bond lengths in the benzene ring match well to literature and that the benzene is not as aromatic or symmetric as normal benzene backed up roughly by MO visualisations of the molecule. This molecule could be researched in much more detail with other calculations however there is not time to do this in this project.

Conclusion to Mini-Project and general comments on Computational Methods

Overall this mini-project has revealed useful information about the properties of superacids and how they can be changed. It has also shown the accuracy of computational methods on explaining observed properties of molecules in a solid and logical manor. It has been shown that superacids can be changed by changing the type/number of substituents on them. It has also shown that charge analysis can be used in order to look at the localisation of charge in a molecule (and in this case the site of protonation). The trends have not been prefectly clear in this mini-project's case and is most likely to be down to subtle effects that only MO calculations can explain. Simply looking at electronegativities for example in this case doesn't identify subtle trends but only large scale trends. I am not aware if any other superacids of the type studied in this project have been studied (none have been found) but would be interesting to know if indeed, for example, the fully fluorinated superacid is a weaker acid than the fully chlorinated version. This is one of the beauties of computational chemistry; that new and exotic molecules can be theoretically studied and have properites predicted without out the need for synthesis.

Computational methods are cheap, efficient ways of looking at and explaining properties of molecules that couldn't be explained in any other way. Qualitative MO can be used in simpler cases (as above in BH₃) to look at orbital shapes and rough relative energy levels but can't give energy numbers (computational can be used). These energies are very useful in studying reactions as in this mini-project. As the complexity of the molecule increases using computational MO calculations can save time in looking at the form of the orbitals and in some cases is the only way (in qualitatively impossible cases) to look at the orbitals. The accuracy of the calculations made are very good in nearly all cases to observed experimental values but there is bound to be small error introduced by approximations used in the calculations as seen but these approximations allow the calculations to be done with a good balance of accuracy and time.