Rep:Mod:EYAAWKK&^

3rd Year Computational Chemistry Lab

Module 1- Structure and Spectroscopy (molecular mechanics and molecular orbital)

In this first section of the experiments the Molcular mechanics model will be used to find lowest energy conformations of molecules as to investigate characteristics and reactivity. The Molecular mechanics model (MM) works simply by assuming that the energy of molecule is equal to the sum of five terms that are non-interacting:

1. The sum of all diatomic bond stretches (each expressed as a simple Hookes law potential).

2. The sum of all triatomic bond angle deformations (also a simple Hookes law potential).

3. The sum of all tetra-atomic bond torsions (a cosine dependance).

4. The sum of all non-bonded Van der Waals repulsions (using a simple 6/12 potential).

5. The sum of all electrostatic attractions of individual bond dipoles.

Using force constants and other such parameters MM tries to minimise the energy of the molecule by adjusting bond lengths, bond angles and torsion angles. The model is useful for finding the optimised geomtery, total energy of a molecule as well as the contibution of the 5 above terms to the total energy. The specific type of molecular mechanics that will be used in this experiment is the MM2 method.

Experiment 1-The Hydrogenation of the Cyclopentadiene Dimer

In this experiment the formation (cycloaddition: _π4_s + _π2_s ) and hydrogenation of the cyclopentadiene dimer will be investigated. The energy differences between molcules 1-4 in their optimum geometries (using MM2 in ChemBio 3D) will be considered and this will give and indication of the thermodynamics of the reactions. By looking at these numbers one can suggest whether the reactions (cyclopentadiene dimerisation; dimer hydrogenation) are either thermodynamically or kinetically controlled. The molecules that are being looked at can be seen as to follow:

Reactants and Products for Experiment 1:

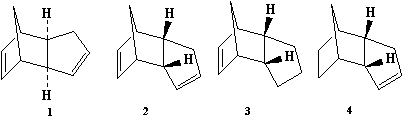
To use ChemBio 3D the structures are drawn in 2D (as in chemDraw) and then the programm converts automatically to 3D coordinates that can be saved as .mol or .gjf files. Calculations can then be run on the drawn molecules. 1-4 were analysed using the MM2 force field option in ChemBio3D Ultra and gave the following outputs of energies and coordinates (Jmol):

Note: molecule 3 had two lowest energy conformations (3a and 3b) where the five membered ring was either bent under the rest of the molecule or bent out from the rest of the molecule. The bent out conformer is slightly lower in energy as can be seen below but both have been included below. In the other cases (1,2&4) the molecules really have to space for change on as such the lowest energy conformer was simple to find

Parameter	Molecule 1-exo dimer	Molecule 2-endo dimer	Molecule 3a-first hydrogenated endo dimer (5membered ring under)	Molecule 3b-first hydrogenated endo dimer (5membered ring out)	Molecule 4-second hydrogenated endo dimer
Stretch	1.2846	1.2283	1.2324	1.2894	1.0925
Bend	20.5690	20.8764	18.8641	19.9343	14.5100
Stretch-Bend	-0.8363	-0.8293	-0.7625	-0.8389	-0.5461
Torsion	7.6630	9.5092	12.2469	10.7537	12.5116
Non-1,4 VDW	-1.4206	-1.5645	-1.5627	-1.2353	-1.0520
1,4 VDW	4.2412	4.3328	5.7523	5.6226	4.5054
Dipole/Dipole	0.3776	0.4490	0.1631	0.1620	0.1407
Total energy/kcalmol-1	31.8785	34.0019	35.9337	35.6878	31.1620

Discussion and relevence of the found energies

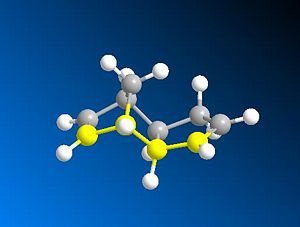
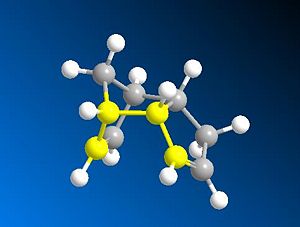
The dimerisation of cyclopentadiene occurs to give the endo product (2). However if one looks at the energies for the exo(1) and endo(2) products they can be seen to be 31.8785 and 34.0019kcalmol^-1 respectively (a difference of 2.1234kcalmol^-1). The main reason for the difference in energy between the endo and exo form is due to a difference in torsional strain. In the exo form the torsional strain is 7.6630kcalmol^-1 whereas in the end form is is increased to 9.5092kcalmol^-1 (a difference of 1.8462kcalmol^-1-accounting for 87% of the increase in total energy). This torsion difference is seen when looking at the dihedral angle across the new formed C-C bond i.e. the dihedral angle of C-C-C-C across the new formed C-C bonds (one bond shown highlighted in the images below). The angles for the exo(1) form are 179.9degrees and 177.6degrees and for the endo (2) form are -45.3degrees and 51.5degrees. This means that in the exo case the C-C bonds and close to antiperiplanar (app) to each other and in the endo case C-C bonds are roughly gauche (synclinal) to each other. This increase in energy between app and gauche is down to two factors. Firstly a major steric effect thought to be simply down to bond electron bond electron repulsion which favours a staggered conformation over eclipsed, and secondly an electronic factor which also favours staggered over eclipsed as it allows σ-σ* overlap between app bonds and leads to stabilisation. The steric effect is the reason why app is favoured over gauche, which are both eclipsed, simply because the two carbons are prefered to be as far apart as possible due to steric clashes.

Exo dimer	Endo dimer

This means that despite the fact that the endo product is thermodynamically less stable it is the one formed in the reaction. This shows therefore that the reaction must be kinetically controlled and that the kinetic product must be the endo form.

The reason for the kinetic preference of the endo product can be explained simply by favourable secondary orbital interactions. The endo transition state in the is lowered in energy due to additional secondary overlap interactions between occupied and unoccupied orbitals in the system (a lower energy transition state means it is favoured kinetically due to a lower activation energy) where as the exo has no such interactions. This is illustrated below from literature and also from a selfdrawn Chemdraw Diagram:

A digram showing stabilising secondary orbital overlap in the endo transition state but not in the exo transition state

Stablising Secondary orbital interactions in the endo transition state in the Dimerisation of Cyclopentadiene

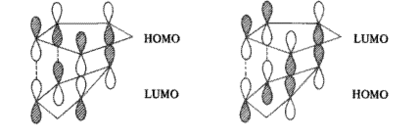
Next one can compare the energies for hydrogenated endo products 3 (we'll use the lowest energy 3b) and 4 to see which is the most thermodynamically favoured hydrogenation. The energies are 35.6878 and 31.1620kcalmol^-1 respectively (a difference of 4.5258kcalmol^-1) and thus show that 4 is the most thermodynamic hydrogenation. This might be expected such that the strain resulting from the carbon carbon double bond being so close the the methyl bridge is relieved in forming 4 whereas in 3 the less strained double bond is reduced which is not as favourable. Another way to look at this is to say that in relieving the strain in the ring next to the bridge strain is relieved in two ring systems (by nature of the bridge adding another ring system that the double bond is involved in) whereas by hydrogenating the other double bond less strain is relieved. To look at this in terms of a reaction it is best to compare 2 to 3 and then 2 to 4.

On going from 2 to 3(b) there is an increase in stretch (1.2894-1.2283=0.0611kcalmol^-1) but this only minor. There is a slight decrease in bend (19.9343-20.8764=-0.9421kcalmol^-1) which again is only minor. The Stretch-bend stays roughly the same wth only 0.0096kcalmol^-1 decrease. Torsion increases (10.7537-9.5092=1.2445kcalmol^-1). non-1,4 VDW increases by only a small amount (1.5645-1.2353=0.3292kcalmol^-1). 1,4 VDW increases (5.6226-4.3328=1.2898kcalmol^-1). Dipole dipole decreases (-0.4490+0.1620=-0.2870kcalmol^-1). Overall these slight increases and decreases amount to having an overall rise in energy on going from 2 to 3(b) of 1.6859kcalmol^-1 (35.6878-34.0019kcalmol^-1). This is why this reaction is rendered unfavourable when compared to the next discussion. The main contributors I would say are Bend ,Torsion and 1,4 VDW. Bend goes down quite a lot on hydrogenation of the double bond in this case but not enough to counter the large increase in Torsion and 1,4 VDW that occurs.

Now to compare going from 2 to 4 there is a decrease in Stretch (1.0925-1.2283=-0.1358kcalmol^-1) which is a larger decrease than the last reaction. Bend decreases (14.51-20.8764=-6.3664kcalmol^-1) by a large amount when compared to the above reaction. Stretch-bend increases (-0.5461+0.8293=0.2832kcalmol^-1). Torsion increases (12.5116-9.5092=3.0024kcalmol^-1) by more than in the last reaction. Non-1,4 VDW increases slightly (-1.0529+1.5645=0.5125kcalmol^-1) by only slightly more than in the previous reaction. 1,4 VDW increases only slightly (4.5054-4.3328=0.1726kcalmol^-1) and less when compared to the other reaction. The Dipole-Dipole decreases by (0.1407-0.4490=-0.3083kcalmol^-1) roughly by the same amount as before. All of these effects lead to a decrease of 2.8399kcalmol^-1 (34.0019-31.1620kcalmol^-1) in this case on going from reactant (3(b)) to product (4). The main reason for this despite the significant increases in Torsion and non-1,4 VDW there is a large decrease in Bend.

Thus overall on going form 2 to 4 there is an increase in energy (thermodynamically unfavourable) which is mainly due to the fact there is only a slight relief in bend strain which is is not enought to counter the increases. On going from 3(b) to 4 howvee the relief in bend in large enough to counter the increases and this lead to an overall decrease in energy on hydrogenation rendering it thermodynamically more favourable. The difference in relief of the bend strain in each case fits in with the above arguement of how the strain in the rings would be expected to be relieved on hydrogenation.

3 and 4 can also be compared directly also in detail in order to get a better idea of what is occuring. From looking intially at the above table it can be seen that the major difference in the total energies comes from the difference in Bend (19.9343-14.5100=5.4243kcalmol^-1). This is as previously stated due to the relief of the extremely strained alkene and close proximity bridge combination. 4 does have a higher torsional contribution (12.5116 compared with 10.7537kcalmol^-1 a difference of 1.7579kcalmol^-1) than 3b but this is then made up by a lower 1,4 VDW contibution in 4 when compared with 3(b) (5.6226 compared to 4.5054kcalmol^-1 a difference of 1.1172kcalmol^-1). The change in contribution from stretch, stretch-bend, dipole-dipole and non-1,4 VDW is minimal (changes of -0.1969, 0.2928, 0.0213, 0.1833kcalmol^-1 respectively). This ultimately leads to the same conclusion as the above arguement.

Experiment 2-Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue)

In this part of the experiment the two below reactions are to be studied using the MM2 method. The reactants and their lowest energy conformations will be looked at specifically in each and how this effects the stereochemistry of the product.

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue) Reaction 1,

Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD+ analogue) Reaction 2,

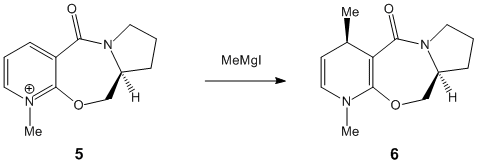
Initially the first reactant (5) was put into ChemBio 3D and the structure was investigated in order to find its lowest energy conformation. In this case te MeMgI was not put into the structure. The reason for this being that when it was put into the structure and the MM2 method was ran the Mg did not allow the calculation to be run: "molecular mechanics parameters are available only for certain types of bonds, and frequently are not available for many functional groups. Metal ions are also a category less easily handled at present by this type of model". The reason for this is simply that the MM2 method must have the force contants for particular bonds, bonds angles and torsions and the numbers are not known for Magnesium in this struture.

Once the first structure was entered into the programme the MM2 was ran and a structure was found (Conformation 1). This structure had the carbonyl group at a positive angle of around ~40degrees (i.e. above the plane of the aromatic system). In order to try and minimise the next structures energy the carbonyl oxygen was manually moved to a larger angle and the 7 membered ring was manipulated from its lowest energy state as to see if any potential energy wells were overcome.This resulted in a slightly lower energy than before but nothing significant. Next the carbonyl was dragged slightly below the plane fo the double ring system and again the 7 membered ring manipulated as so all the atoms were moved into random positions. This resulted again in the carbonyl being above the plane of the ring (positive angle) but this time at a lower angle (~20degrees). This position was higher in energy than the higher angle ~40 degrees systems. This was repeated again with slight manipulation of all the atoms and then settled back again to around ~20degrees woth an ever so slight improvement in energy and then this process once more was repeated with dragging the carbonyl O significantly below the plane of the double ring system and manipulating the surrounding atoms as to try and force the carbonyl below the plane. This again resulted in the carbonyl moving back to a positive angle of ~20degrees. Thus no matter which way this is looked at the carbonyl group oxygen will be found above the plane of the double aromatic ring system although when around ~45degrees is the best in terms of total energy. It can be seen the main difference between the larger angled (~40degrees) and the smaller angled (~20degrees) is a that the bend increases significantly but the torsion goes down a lot also (altohugh by slightly less than the increase) leading to only a small increase in total energy on going from ~40 degrees to ~20 degees. Below are the results for all trialed systems with the Jmol 3D coordinates for the lowest energy system:

Parameter	Reaction 1- Conformation 1	Reaction 1- Conformation 2	Reaction 1- Conformation 3	Reaction 1- Conformation 4	Reaction 1- Conformation 5
Stretch	0.9268	0.8742	1.1798	1.1733	1.2027
Bend	6.6585	6.7351	11.3745	11.4175	11.6333
Stretch-Bend	0.1184	0.1191	0.0521	0.0522	0.0521
Torsion	9.9064	9.5263	5.1615	5.0686	4.9091
Non-1,4 VDW	-2.4794	-2.6651	-2.0527	-1.9981	-1.8865
1,4 VDW	11.5718	11.5374	11.8603	11.8869	11.8994
Charge/Dipole	3.2912	3.2212	2.6963	2.6800	2.6238
Dipole/Dipole	-3.7797	-3.8030	-3.9525	-3.9659	-3.9961
Total energy/kcalmol-1	25.9138	25.5452	26.3193	26.3144	26.4378
Dihedral angle with the plane of the aromatic ring system (C=C-C=O)/degrees	43.3645	41.5749	25.7611	23.9143	21.0936

Lowest energy conformer of Reactant 5-Conformer 5

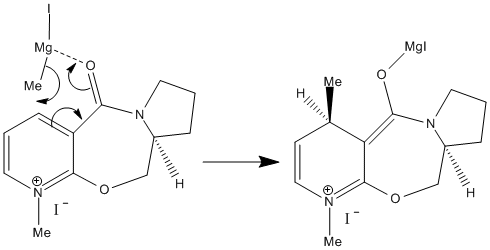
In terms then of the effect of this in the stereochemistry of the product on must look specifically at the nucleophile. In this case it is a Grignard reagent which contains the electron deficient mercury atom. The nature of the Grignard allows possible coordination of one of oxygen sp² lone pairs to the Mg atom. This coordination then effectively guides the Methyl group onto the top face of the ring system resulting in the sterochemistry as seen in product 6. . also note that the reagent itself is also quite small (Methyl) and so steric factors are not enough to overcome this co-ordinating factor) This can be seen in the below reaction mechanism as adapted from literature:

Grignard reagent co-ordinating nucleophilic addtion

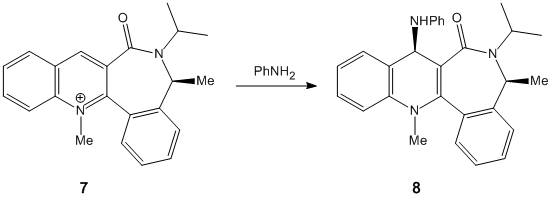
Next the second reaction was studied and the lowest energy conformation of the reactant (7) found. The molecule was drawn and then the MM2 method ran giving the first energy minimum conformation. The energy of this was then attempted to be lowered in a simlar method to the previous and the carbonyl oxygen was moved below the aromatic ring system and the calculation ran. The C=O bond returned to a positive angle and the molecule ended up at much the same energy with a slight reduction. Next to lower the energy the phenyl ring system attached to the 7 membered ring was moved manually to a more vertical position and the seven membered ring generally manipulated to accomodate this. This again lead to a decrease in energy but only by a small amount of 1.2194kcalmol^-1. The next thing that was attempted was to try and force the carbonyl C=O bond such that the angle was below the ring system but in order to do this the whole of the non-aromatic part of the molecule was inverted (ensuring the stereochemistry of the Me is maintained as "up"). Also the above conformational adjustments which are known to decrease the energy of this molecule were taken to account in this calculation(more vertical ring etc.). This did lead to a decrease from the previous lowest value of 19.7499kcalmol^-1 to 14.8066kcalmol^-1 (a decrease of 4.9433kcalmol^-1. A furthur general manipulation and calculation to try and reduce the energy was ran but this resulted in a slight increase in energy. Thus the lowest energy conformation was conformation 4. This lowest energy is most likely the prefered conformation and does explain the resultant stereochemistry in the product as explained later. Here are the energies of the run calculations including angles of the carbonyl relative to the ring system:

Parameter	Reaction 2- Conformation 1	Reaction 2- Conformation 2	Reaction 2- Conformation 3	Reaction 2- Conformation 4	Reaction 2- Conformation 5
Stretch	1.7634	1.7347	1.7476	1.5677	1.5679
Bend	10.5700	10.2752	9.4026	6.4987	6.4975
Stretch-Bend	0.3929	0.3978	0.3976	0.3348	0.3350
Torsion	-6.0098	-6.0367	-6.1888	-6.2077	-6.2056
Non-1,4 VDW	-0.8211	-1.1583	-1.2485	-2.6115	-2.6114
1,4 VDW	18.0302	18.0937	17.8830	17.6476	17.6472
Charge/Dipole	2.5552	2.4869	2.5486	2.3804	2.3806
Dipole/Dipole	-4.8230	-4.8238	-4.7922	-4.8048	-4.8047
Total energy/kcalmol-1	21.6579	20.9696	19.7499	14.8051	14.8066
Dihedral angle with the plane of the aromatic ring system (C=C-C=O)/degrees	43.9745	41.0928	45.1442	-43.0919	-43.0893

Lowest Energy Conformer of Reactant 7-Conformer 5

Unlike in the first reaction of this section, in which a Grignard reagent was the nucleophile, in this reaction the incoming nucleophile (PhNH₂ has no co-ordinating ability and is sterically large (-Ph). Thus overall sterics determine the stereochemistry of the product in this case. Since the lowest energy conformation is that with the carbonyl pointing down the nucleophile is guided onto the less hindered (top) face of the aromatic system. Overall this part of the experiment has shown that energy minimisations even at this basic MM2 level can give a good idea of what can be expected from a reaction by combining prior chemical knowledge with an energy optimised conformation structure of a molecule.

The next thing to answer is how this modelling can be improved. Using the simplistic Mechanics MM2 model is limited as it is based simply on known parameters and force constants derived from well known and characterised molecules (interpolative technique). A better approach to modelling is to consider the electronics of the reaction which MM2 cannot do. Knowing and considering orbital interaction in reactions and molecules gives a far better idea of what is actually going on and is a more direct approach to the problem. If one understands the electronic properties of a reaction then one can truely understand what is going on (reactants and paths to products via transition states and intermediates-now can model kinetic control); this can't be understood using molecular mechanics. Also Spectroscopic and bonding properties can be found accurately using this approach and this will be seen later on in this module . Another limitation of MM due its interpolative nature is that new or different molecules can't be modelled. This was seen earlier on in the module when a Grignard was trying to be included in the calculation but the required parameters were simply not there. This type of problem requires a complete MO (quantum mechanics) model which will be seen later in this module. MO theory also has to be used to explain other subtle effects that MM can't take into account that involve orbital overlap and interaction (aromaticity, steroelectronics etc.)

In the preliminary part of the project work later on an interesting difference to the two different treatments (MM and electronic) can be realised in spectroscopic calculations. This is due to the required more complicated treatment of the orbitals rather than simple Molecular Molcular Mechanics parameters being applied.

Experiment 3-Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

In this part of the experiment atropisomerism will be explored in an intermediate in the synthesis of Taxol. The two isomers can be seen below:

Atropisomers

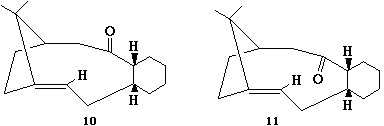
The chemical structure was initally drawn in ChemBio3D and the carbonyl manipulated such that it was pointing up and then a MM2 minimisation calculation ran (54.4164kcalmol^-1). Next the six membered ring conformation was considered in order to reduce the overall energy. The initial boat conformation was changed to a chair and a few atoms moved away from their positions and an MM2 minimisation was run. This did indeed lead to a decrease in energy to 48.8873kcalmol^-1. A final attempt to lower the energy by general manipulation of most of the atoms from their current position and then running an MM2 was made but resulted to a slight increase in energy to 48.8946kcalmol^-1. Thus the previous conformation was taken as the lowest energy one for this isomer.

After this the carbonyl was moved away from up to pointing more in in the outwards direction from the ring. After running MM2 minimisation the energy output was significantly high (124.6797kcalmol^-1). Looking at the molecule the increase in energy was obviously from the strain in the carbonyl in which the C-(C=O)-C angle is 163.9 degrees (and bent in the opposite direction to expected-see below)

. Looking at the output data the major increase in tottal energy resulted mainly from an increase in bend and an increase in 1,4 VDW.

Next the carbonyl was moved into a downwards direction and immediately this lead to a drop in energy (50.8064kcalmol^-1) when compared to the up isomer. To then try and reduce the energy furthur the six membered ring was manipulated as to change it from its boat conformation into its chair conformation and an MM2 minimisation run. This did in fact lead to a decrease in energy to 44.2804kcalmol^-1 (a decrease of 6.5260kcalmol^-1). This was the lowest found energy for when the carbonyl group is pointing down.

The energy output data can be seen below along with the Jmol 3D coordinates for each atropisomer(up/down)and their lowest conformer: Nb: The conformers are simply named in the order in which the calculations were run above, although there is an extra row specifying the position of the carbonyl group (up/down/~orthongonal) in each case for clarity

Parameter	Taxol- Conformation 1	Taxol- Conformation 2	Taxol- Conformation 3	Taxol- Conformation 4	Taxol- Conformation 5	Taxol- Conformation 6
Carbonyl orientation	Up	Up	Up	Orthogonal	Down	Down
Stretch	2.8206	2.6911	2.6828	4.5044	2.7832	2.5635
Bend	16.4268	15.8426	15.8841	76.6523	12.2412	10.7793
Stretch-Bend	0.4564	0.3920	0.4061	-0.0287	0.3649	0.3276
Torsion	21.3871	18.1648	18.2076	20.0432	22.6158	19.6683
Non-1,4 VDW	-0.8460	-0.9765	-1.1186	-1.3563	-0.7518	-1.4412
1,4 VDW	14.0341	12.6254	12.6852	24.9588	13.7437	12.5633
Dipole/Dipole	0.1375	0.1479	0.1475	-0.0941	-0.1907	-0.1805
Total energy/kcalmol-1	54.4164	48.8873	48.8946	124.6797	50.8064	44.2804

Lowest Energy conformer for "carbonyl-down" atropisomer-overall lowest energy atropisomer

The difference between the two atropisomers is (48.8946-44.2804=)4.6142kcalmol^-1. This difference in mainly down to an increase in bend (15.8841-10.7793=5.1048kcalmol^-1 on going from the "down" to the "up" atropisomer. If one measures the angles in the carbonyl groups in each case the following can be seen:

down = 120.2degrees(C-C-C), 120.0degrees(C-C=O), 119.7degrees(C-C=O)

up = 126.3degrees(C-C-C), 118.1degrees(C-C=O), 115.3degrees(C-C=O)

This then explains the increase in bend on going from down to up. The carbonyl angles are all close to the expected 120degrees expected around this carbon sp² centre in the down isomer, however in the up isomer the angles can be seen to deviate significantly from this 120degrees (maxiumum deviation of 6.3degrees) and so increasing the bend contribution to the energy.

Another interesting point to note the angle between the carbonyl and the alkene in each case. In the "up" scenario the angle is 92.6degrees and in the "down" scenario is 112.7degrees. i.e. in the up case the carbonyl is towards the alkene and in the down case is pointing away.

The alkene in this type of system has also been seen to display a decrease reactivity. This seems strange at first given the strained nature of the double bond (Bredt's rules) which would perhaps make it appear more reactive: "A double bond cannot be placed at the bridgehead of a bridged ring system, unless the rings are large enough". The difference in this case is that in fact the ring system is large enough (10-membered) to mean that this bridgehead alkene is not unstable due to this rule. So why is it this alkene is actually so unreactive? This is again down to the size of the ring. Since the ring is actually quite large (10carbons) it is beneficial to have some sp² carbon centres in the ring. There is disfavour of having the furthur sp³ centres instead of the two sp² centres in this size of ring due to the introduction of transannular and other types of strain (bend will be seen to be the most prevalent) in the ring on rehybridisation. This can be crudely tested by modelling the hydrogenation of the alkene. If this energy increase is large on simple hydrogenation then on functionalisation by more sterically demanding groups one would expect to have an even larger effect.

If one takes the most stable conformer of the most stable atropisomer (carbonyl down) and hydrogenate the double bond the energy goes up to 67.2043kcalmol^-1. This is a significant rise of 22.9239kcalmol^-1. A rise in energy obviously shows a thermodynamic disfavour in going to this state. This large increase in energy on hydrogenation of the alkene is due to an increase in stretch, bend,stretch-bend, non-1,4 VDW, 1,4 VDW and Dipole/Dipole. One can also see the expected transannular strain introduced on rehybridisation of the sp² centres to sp³ (highlighted in the diagram below). This transannular strain can be seen in the increase in non-1,4 VDW of 4.5153kcalmol^-1. The main cause of the increase is the bend contribution which increases by 12.5122kcalmol^-1 on introducing sp³ centres into this large ring system. On functionalisation by larger groups this effect could be even larger and so making this reaction even more unfavourable and hence slow.

An image showing the transannular strainon the hydrogenation of the alkene bond

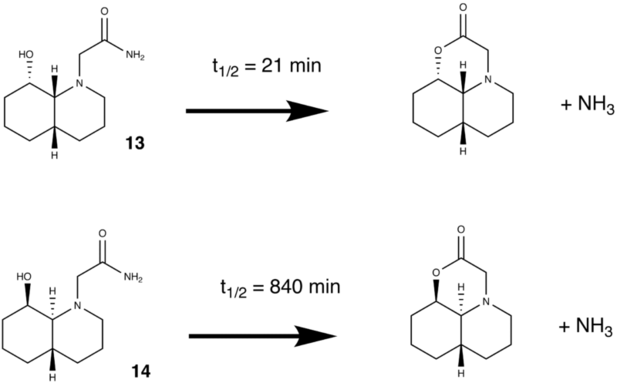
Experiment 4-Room Temperature hydrolysis of a peptide

In this exercise a particular pair of reactions in which hydrolysis of a peptide occurs were studied. In both cases the hydrolysis takes place quickly when compared with 500years (the time taken usually for a normal peptide bond to hydrolyse under these conditions). However one of the reactions takes even less time to occur than the other (21mins compared to 840mins). The reasons for this will be investigated through modelling the lowest energy conformer in each case and considering various factors about the reaction these are:

1. Hydrogen bonding which may stabilise the structure.

2. The angle of approach of the the OH group on the C=O bond (Burgi-Dunitz angle).

The Reaction Schemes studied can be seen below:

Room Temperature Hydrolysis of a peptide

Thus the strategy in this part of the experiment it too find the lowest energy conformer in each case first and then to perform analysis on this lowest energy structure (since this lowest energy structure is the one which will exist predominantly in thermodynamic reversible conditions)

The first thing that was done in order to proceed with this experiment was to firstly draw the cis decalin base unit and then to minimise the energy. This was simply to ensure that the correct cis (not trans) was drawn initially with the correct, double boat, conformation. It was also considered that the cis-decalin system has the ability to ring flip. In the journal with reference to this reaction the "down" -OH is equatorial and so this is how it shall first be considered (Nb: Considering ring flipping the -OH could be axial or equatorial). The N group can then also be equatorial or axial and there is an equilibrium between the two. This is simply due to the fact that nitrogen can flip through a trigonal planar geometry in order to invert its stereochemistry at room temperature. The position of the equilibrium (below) can be found by modelling the two possible configurations and comparing the lowest energy conformer in each case to each other.

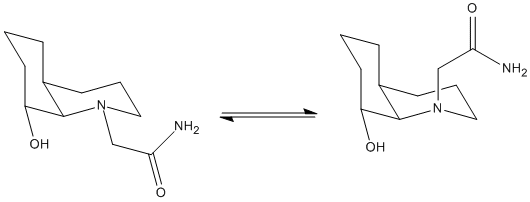
The first tried isomer was that with the -OH group and the peptide group (actually ethylamido group but is refered to as peptide from now on in terms of axial-eq stereochemistry) equatorial (as seen on the left in the equilibrium above). The molecule was drawn in ChemBio 3D by modifying the cis-decalin base unit that was already drawn (ensuring chair-chair conformations)and then an MM2 minimisation calculation run in order to give an initial energy of 17.8692kcalmol^-1. The peptide group was then manipulated both around the methylene C to ring C bond and rotated around the methylene to C(=O) bond in order to a lower energy of 15.3637kcalmol^-1. The energy was attempted to be minimised by rotating the -OH around such that it was app to the CH in the ring but this only resulted in a higher energy of 16.2342kcalmol^-1. Thus the previous model was loaded and manipulated until a lower energy of 14.0490kcalmol^-1 was found and then the lowest of 13.3521kcalmol^-1.

The next isomer that was tried was then the one, keeping the OH equatorial, with the peptide group now axial to the ring in which it is contained (on the right in the equilibrium above). The first found energy after forming the molecule in ChemBio 3D (by again modifying the base chair-chair unit) was 26.1760kcalmol^-1. To then minimise this the NH₂ was interchanged with the O in C=O by rotation; also the OH was rotated away from the cluttered ring systems. This resulted in an energy of 19.2852kcalmol^-1. Furthur manipulation and minimisation resulted in a lowest found energy of 19.2775kcalmol^-1 and this was the lowest found energy. The results for these two isomers can be seen below:

Parameter	Peptide 1- Conformation 1	Peptide1- Conformation 2	Peptide1- Conformation 3	Peptide1- Conformation 4	Peptide1- Conformation 5	Peptide 1- Conformation 6	Peptide1- Conformation 7	Peptide1- Conformation 8
Peptide orientation	Equatorial	Equatorial	Equatorial	Equatorial	Equatorial	Axial	Axial	Axial
OH orientation	Equatorial	Equatorial	Equatorial	Equatorial	Equatorial	Equatorial	Equatorial	Equatorial
Stretch	1.7640	1.8066	1.7974	1.6136	1.7000	1.6547	1.4189	1.4408
Bend	4.9229	6.2780	6.0685	5.9898	5.3341	7.8749	7.8123	7.8543
Stretch-Bend	0.5260	0.5944	0.5964	0.6008	0.5789	0.6730	0.5888	0.5979
Torsion	7.7194	7.7856	8.4665	8.6138	8.3045	10.5158	11.5356	11.6077
Non-1,4 VDW	-3.1225	-5.4290	-5.4875	-5.4478	-5.9432	-2.7271	-8.0857	-8.2044
1,4 VDW	9.6296	9.2354	9.5255	9.3851	9.4861	9.6295	10.4828	10.4653
Dipole/Dipole	-3.5612	-4.9072	-4.7325	-6.7062	-6.1082	-1.4447	-4.4675	-4.4840
Total energy/kcalmol-1	17.8692	15.3637	16.2342	14.0490	13.3521	26.1760	19.2852	19.2775

Lowest energy conformer of the equatorial(OH)-axial(peptide) isomer

Looking at this above table the energy difference between the lowest energy conformations in each isomer is 19.2775-13.3521=5.9kcalmol^-1. This is fairly close to the difference in literature of 5.0kcalmol^-1 but is higher by a non-negligible amount. After finding this gave bigger difference than literature value the 19.2775kcalmol^-1 was attempted to be lowerd but this could not be done. Perhaps the lower of the values (13.3521kcalmol^-1 is new energy low that the literature reference did not find. The difference between the next lowest value 14.0940kcalmol^-1 and the 19.2775kcalmol^-1 does give 5.2kcalmol^-1 so perhaps that is what they found. Since then the equatorial-equatorial isomer is the most prevalent(most favoured energetically) by a significant amount there is an effect on the reaction. The peptide hydrolysis only occurs quickly through this most favoured isomer (lowest energy-equatorial-equatorial)and so given that this isomer is energetically favoured this is why this reaction has a small half life of 21mins (this will be contrasted next in the trans-decalin system case). Why this is the isomer that hydrolyses fastest will be discussed later on.

The other conformations that must be considered are that when this cis-decalin ring system has ring flipped in each ring (which is allowed). This moves the -OH to the axial position and again the peptide be either axial or equatorial. This particular set of conformations were not mentioned in the literature but will be looked at anyway out of interest. This might help explain why it is that these two are not considered in the journal and only the previous cis-isomer.

Initially the first energy gained by MM2 minimisation was 22.1580kcalmol^-1. The groups were then manipuated so they were close together (potential for reaction). This lead to an energy of 17.1782kcalmol^-1 and then furthur manipulation such that the carbonyl oxygen and alcohol oxygen were close together giving eventually a lowest energy of 15.4866kcalmol^-1. Furthur manipulation rotating the NH₂group towards the -OH lead to an increase in energy to 21.7420kcalmol^-1 which shows the previous energy is indeed the lowest with the two oxygens together. One might expect this due to the smaller steric demand of O when compared with NH₂.

Next the compound in which the -OH and -CH₂CONH₂ are both axial was experimented with. The inital energy that was found was 21.2045kcalmol^-1. The two groups appeared to be generally in a good low energy conformation. To improve the OH group was rotated into what appeared to be a low energy conformation and the NH₂ moved out of the way of the ring system itself. This lead to a decrease in energy to 19.2472kcalmol^-1. The peptide group was generally manipulated until the lowest energy was then found of 18.8907kcalmol^-1.

The informatation about the energy minimisation can be foud summarised in the below table:

Parameter	Peptide 1a- Conformation 1	Peptide 1a- Conformation 2	Peptide 1a- Conformation 3	Peptide 1a- Conformation 4	Peptide 1a- Conformation 5	Peptide 1a- Conformation 6	Peptide 1a- Conformation 7
Peptide orientation	Equatorial	Equatorial	Equatorial	Equatorial	Axial	Axial	Axial
OH orientation	Axial	Axial	Axial	Axial	Axial	Axial	Axial
Stretch	1.5333	1.3659	1.4614	1.5559	1.5183	1.5415	1.5055
Bend	6.8059	5.6020	7.2633	10.5288	5.5572	5.3606	5.2778
Stretch-Bend	0.6555	0.5565	0.6574	0.7506	0.5965	0.5951	0.5875
Torsion	9.8982	8.3012	9.5553	9.1178	10.8418	10.1539	10.4846
Non-1,4 VDW	-3.1211	-5.1144	-6.9199	-4.4487	-3.7545	-4.077	-5.1486
1,4 VDW	9.5204	9.6361	9.7941	8.7437	9.5173	9.5098	9.7169
Dipole/Dipole	-3.1343	-3.1691	-6.3249	-4.5062	-3.0721	-3.5063	-3.5328
Total energy/kcalmol-1	22.1580	17.1782	15.4866	21.7420	21.2045	19.2471	18.8909

Lowest energy conformation (peptide axial; -OH axial) in the cis-decalin type system

The energies seen here might show why it is that the other two isomers previously are the ones discussed in literature. The lowest energy of all the cis isomers is that in which both of the groups are equatorial. However the second lowest is that with both groups axial, but this is not considered in the equilibrium in the journal. This may be due to some kinetic effect in which TS must be considered. Ultimately this is not important because the lowest energy (and most reactive) in this case conformer is clear cut. It is interesting to note however that the second isomer in the journal (OHeq,PEPTIDEax) isn't in fact the second lowest in energy. This shows there is likely to be more to this than discussed in the journal and is odd that these other cis-decalin isomers haven't been considered.

The next thing to look at is then the trans-decalin isomer of this. In this case there are in fact only two isomers possible with the specified sterochemistry in total due to the rigidity of the trans-decalin system (no ring flipping). Thus the -OH is always axial in both cases; it is only the position (axial, equatorial) of the peptide that can vary.

The first isomer that is trialed is with the peptide axial The molecule was prepared as before and then a MM2 minimisation ran resulting in an inital energy of 16.7957kcalmol^-1. The peptide was then rotated around the C(=O) to methylene C bond such that the (C=)O was exchanged with the NH₂ and minimised resulting in an energy of 14.1062kcalmol^-1. Furthur manipulation of the peptide carbonyl and amine and the OH group led to an increase in energy to 20.0441kcalmol^-1. This means going back a step and applying furthur manipulation until a lower energy is reached.The lowest found possible energy was 11.9695kcalmol^-1

Now the peptide group was moved to its equatorial position and a minimisation ran. An inital energy minimum of 16.4862kcalmol^-1 was attained. Next the peptide carbonyl oxygen was moved close to the OH group by rotation about the C(=O) and methylene carbon bond and minimised resulting in an energy of 15.4195kcalmol^-1. Furthur careful and tactical manipulation of the peptide and OH group gave an energy of 12.0252kcalmol^-1 and finally a lowest energy of 9.0313kcalmol^-1,

This information can be seen summarised in the below tables:

Parameter	Peptide2- Conformation 1	Peptide2- Conformation 2	Peptide2- Conformation 3	Peptide 2- Conformation 4
Peptide orientation	Axial	Axial	Axial	Axial
OH orientation	Axial	Axial	Axial	Axial
Stretch	1.5522	1.6897	1.6371	1.5304
Bend	5.4083	5.4764	5.4854	5.0737
Stretch-Bend	0.5585	0.6056	0.5950	0.5467
Torsion	9.4557	8.7344	8.2941	8.7489
Non-1,4 VDW	-5.0297	-5.1038	-1.9264	-7.1063
1,4 VDW	9.4178	9.5251	9.1273	9.6262
Dipole/Dipole	-4.5671	-6.8211	-3.1684	-6.4499
Total energy/kcalmol-1	16.7957	14.1062	20.0441	11.9695

Parameter	Peptide2- Conformation 5	Peptide2- Conformation 6	Peptide2- Conformation 7	Peptide 2- Conformation 8
Peptide orientation	Equatorial	Equatorial	Equatorial	Equatorial
OH orientation	Axial	Axial	Axial	Axial
Stretch	1.5422	1.5138	1.4942	1.5180
Bend	4.3148	4.0068	4.0789	3.2125
Stretch-Bend	0.5694	0.5621	0.5133	0.4823
Torsion	6.3210	6.4816	7.3354	7.2599
Non-1,4 VDW	-3.4941	-3.3524	-6.8349	-8.1527
1,4 VDW	9.0900	9.0744	9.9326	9.8025
Dipole/Dipole	-1.8570	-2.8667	-4.4944	-5.0911
Total energy/kcalmol-1	16.4862	15.4195	12.0252	9.0313

The difference between the lowest energy conformer in the axial peptide case to the equatorial peptide case is 11.9695-9.0313=2.9kcalmol^-1. Which again matches closely with literature (3.1kcalmol^-1). This means that the equilibirum is in favour of the equatorial peptide. However in this case it is the other (axial peptide) isomer that actually undergoes the peptide hydrolysis quickly. Hence why this reaction has a longer half life of 840mins.

In summation the first cis-declain system finds its equilibirum preferentially in a form which undergoes hydrolysis quickly whereas the in the second trans-decalin type molecule finds itself on the side of the equilibrium in which the hydrolysis doesn't happen quickly. This fact that these particulat isomers are the ones that are preferentially adopted has been supported by the MM2 calculations in this experiment.

Can one again in this case explain why it is the axial peptide isomer is the most reactive? This will be looked at in the next section.

Another point to make in this experiment is in fact how much quicker peptide bonds in both of these molecules hydrolyse when compared to 500years (normal peptide bond under normal conditions-at neutral pH and 25°). This is simply because in both cases there is a potential intramolecular peptide hydrolysis. Being intramolecular in this way increase the probability of a reaction occur and so occurs faster than if a water molecule had to meet the peptide to hydrolyse it. Effectively the two reactants are being held together increasing the chance of their "collision" and hence reaction. Addititive to this is that in all reactive cases (as seen below) the groups are not only intramolecularly attacking but are also being held together in a close proximity by hydrogen bonding. This is an additive effect to simply just being the intramolecular effect.

Lowest energy conformer in Trans-decalin based molecule with equatorial peptide

Is it then possible to try and justify why the particular conformations are more reactive than others? Lets look at the hydrogen bonding (dipoles), attack angles and distances between the two in the following table:

Cis/Trans decalin	-OH position	Peptide position	H-bonding (as seen by pressing ctrl+H in Chem Bio 3d	Dipole-Dipole contribution	Distance between carbonyl C and OH oxygen/angstroms	Angle of attack on carbonyl carbon /degrees
cis	eq	eq	yes	-6.7082	3.112	57.7
cis	eq	ax	no	-4.4840	3.637	177.4
cis	ax	eq	yes	-6.3249	3.275	51.1
cis	ax	ax	no	-3.5328	4.995	141.7
trans	ax	ax	yes	-6.4499	2.917	68.0
trans	ax	eq	yes	-5.0911	3.022	62.0

In order to try and justify reactivity H-bonding (stabilise structure) and distance and angle of approach (Burgi-Dunitz angle) will be considered.

In terms of hydrogen bonding one would expect when it is present in a structure there will be increase in stability. This is beneficial to the reaction aslong as , of course, it is holding the molecule in a reactive conformation. To look at this the hydrogen-bonding visualisation was turned on and if it showed up it was recorded as "yes" in the above table. Another good indicator is to look at the Dipole-Dipole energy, where a more negative energy indicates a bigger stabilisation and so hence more hydrogen bonding.

In terms of distance obviously the closer the two reacting atoms the better. Then looking at the angle one must consider the Burgi-Dunitz angle. In order for a hydrolysis reaction to occur at a carbonyl the oxygen must attack at an angle of ~107degrees because this is the approximate angle at which the C=O π*-orbital sits.

Firstly the isomers that are known to be more and less reactive (i.e. the ones discussed in the reference journal) will be looked at first. Then the middle example (not in literature where cis-decalin based system and -OH axial) will be speculated at as to which of the two one would expect to be the most reactive.

In the first cis-decalin case it turns out that the most stable isomer is the one that is most reactive. There is infact hydrogen bonding in the most reactive isomer and not in the less reactive isomer. This can be seen in the dipole-dipole where it is more stable by 2.2242kcalmol^-1. Also this most stable isomer has the groups a lot closer, by 0.525angstroms which would render it more reactive. However in both cases the angles are not close to the Burgi-Dunitz angle. This however is not suprising because one would not expect it to necessarily to sit in the reactive conformation. In any attempt to try achieve a Burgi-Dunitz angle during minimisation there was an increase increase in energy as one might expect due to loss of hydrogen bonding in forcing it into this reactive conformation. This is generally because it was found beneficial to have the sterically demanding NH₂ away from the -OH leading to a "non-Burgi-Dunitz angle orientation" also having the carbonyl O close to the -OH leads to hydrogen-bonding. Looking at the Burgi-Dunitz angle is then perhaps not the most important step in this reaction. An interesting point to consider might be the tetrahedral intermediate in the reaction to hydrolysis (Came to light in a conversation with Henry-Rzepa). However there is not enough time to look at it in this case, but it is a possibility.

However overall in this case it does make sense the most reactive reactive isomer is the one said in the literature when looking at thw two other (non-hydrogen bonding) factors.

Next to look at the trans-decalin case. The most reactive isomer (ax-ax) again has the same advantages over the other isomer as previously. Although both have hydrogen bonding the bonding in the most reactive isomer is stronger (as measured using the dipole-dipole energies) by 1.3589kcalmol^-1. Also the two reacting atoms are closer together in the most reactive case by 0.105angstroms. Again the Burgi-Dunitz angle doesn't seem to have much of a relevance in this case, again trying to force the correct angle always lead to an increase in energy. This is an example of the the Curtin-Hammet principle which states the most reactive conformer isn't always the major conformer.

Thus from the above two discussions one might suspect that in the non-literature discussed example (cis-decalin with the OH ax) that the isomer with the peptide equatorial would be the most reactive one. It has hydrogen bonding unlike the other conformer (shown by a dipole-dipole increase in stabilisation (i.e. more negative) of 2.7921kcalmol^-1. Also the reacting groups are closer by 1.675angstroms. Neither again are in the Burgi-Dunitz angle conformation.

Overall this part of the experiment has shown that MM2 modelling can give good explanations for observed chemical phenomina observed in the lab in some good detail. However the use of MO methods might be useful in discussing the reaction going forward.

Modelling using semi-empirical Molecular orbital theory

In this section the molecule 9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene was used in order to demonstrate semi-empirical Molecular orbital Theory. This theory moves beyond simple Molecular Mechanics and considers the electronics of the molecules. PM3 is specifically the semi-empirical model used in this section. PM3 (Parameterized Model number 3) uses NDDO (Neglect of Differential Diatomic overlap). This method uses 2 gaussian function for the core repulsion function and the parameters are treated as optimisable values (as oppose to other semi-empirical methods (AM1) which take their value from spectroscopical methods. . Semiempirical methods don't explicitly include the 2-electron Hamiltonian, but as a result of are fast to run than a full calculation. In order to be accurate the molecule must be similar to the databased molecules (used in parameterisation). We will see in the below case however that the Semi-emprical method can be sued to well model molecules.

The molecule (9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene) can be seen below:

Dichlorocarbene

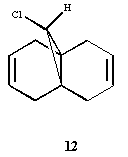
The molecule was firstly drawn in ChemBio3D and minimised using MM2, then saved as a .gjf and then opened in Gaussview in order to perform furthur calculations (MOPAC was not licensed when this point was reached). The Semi-empirical PM3 optimisation was ran in gaussview using gaussian and then the produced PM3 MOs visualised including the HOMO-1,HOMO, LUMO, LUMO+1 and LUMO+2. The Isovalue chosen for the MO visualisations was 0.04 as in the literature journal . The frequency calculation was not run at this point.

When running the calculation the script that was used was:

"# opt pm3"

The orbitals generated can be seen below:

HOMO-1
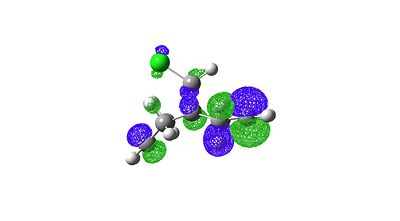HOMO
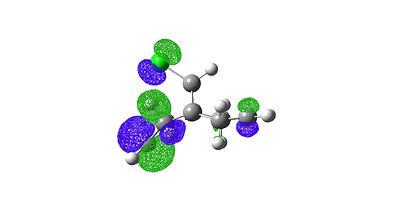LUMO
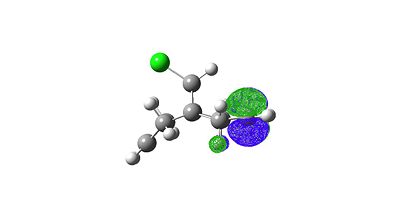LUMO+1
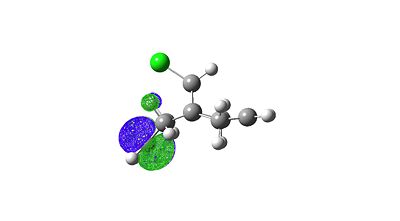LUMO+2

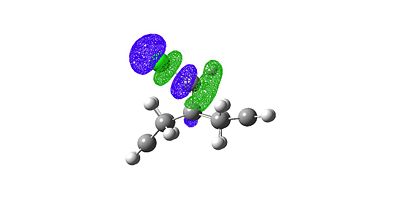When comparing these orbital images to literature they look identical. Also if one inspects the HOMO of the molecule one can see why it is so electrophilic because of the large amount of electron density on the π-bond areas of the HOMO.

The next thing that was done was to run a DFT B3LYP optimisation (discussed in detail in the next section) and frequency calculation using the 6-31g basis set. The script used is as follows:

"# b3lyp/6-31G(d) opt(maxcycle=20) freq"

The DFT optimisation simply fine tuned the optimisation following on from the more crude PM3 optimisation of structure which then lead to a more accurate calculation of the frequencies. Although this was not asked to be done it was thought to simply be an improvement. Here is the Jmol of the finally optimised molecule:

The important frequencies from the output of calculation that require furthur analysis are:

(C=C)= 1740.77cm^-1 (exo, intensity=4.1418), 1760.95cm^-1 (endo, intensity=3.9086)

(C-Cl)= 772.633cm^-1 (intensity=25.2143)

The next step was to hydrogenate the anti(C-Cl) carbon double bond and to optimise and calculate the frequencies in an identical manor to above.

Note the answer to the question in the wiki about the C_s symmetry is that the hydrogenated product is not of C_s symmetry. The change of the sp² centres to sp³ centres breaks this plane of symmetry and gives the resulting product a symmetry of C₁.

The only difference in the calculation was that the optimisation didn't converge after 20 cycles. The max cycles was increased to 50. This didn't converge either. The file was then opened including intermediate geometries and the later geometries compared. There was little change in geometries and so it was deemed unnessecary to include anyfuthur optimisation cyles. Thus this last geometry was submitted for a frequency calculation. Here is a Jmol of the hydrogenated optimised product:

The important output frequencies from this calculation are:

(C=C)= 1761.75 cm^-1(intensity=4.3465) only one double bond in this molecule

(C-Cl)= 777.025cm^-1 (intensity=20.125)

This change in frequency can then be explained using Molecular Orbital Theory. There is an interaction between the exo-π(C=C) orbital and the C-Cl σ* orbtial which leads to stabilisation. This can be seen in the fact that the endo double bond is more reactive than this stabilised double bond, and there is a distortion (proved by the crystal structure) of the double bond towards the bridgehead carbon. This distance can be measured in both the hydrogenated and non-hydrogenated case:

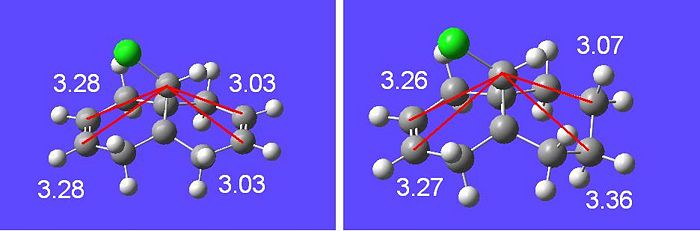
The overlap of the LUMO+2 (C-Cl σ*) in a app fashion with the HOMO-1 (exo-п orbital) leads to a stabilisation of the exo п-orbtial of 0.08eV relative to the HOMO (endo π-orbital). These orbital interactions can be witnessed directly in the calculated values of the stretching frequencies in the molecule. How these orbitals interact can be easily seen looking at the calculated visualised MO digrams above where one can in space how they would overlap.

Firstly looking at the C-Cl frequencies there is an obvious increase in frequency on hydrogenation (777.025-772.633=4.392cm^-1). This can easily explained using the above orbital arguement. With the exo π-orbital present there is a destabilising interaction for the C-Cl bond (overlap with the C-Cl σ*) which weakens the bond. A weaker bond means a lower frequency (see equation-right)

Equation governing frequency dependancy on bond strength (Drawn in Microsoft Word)

. Getting rid of this interaction (by hydrogenation) means the bond is stronger and so a higher frequency is seen.

Now examinining the C=C frequencies there is one frequency that stands out. This is the exo double bond frequency of 1740.77cm^-1 which is significantly lower than the endo double bonds in both the non-hydrogenated and hydrogenated cases (1760.95 and 1761.75cm^-1). This decrease in frequency, seen in the exo double bond when compared to the endo double bond, is simply down to a movement of electron density from the п bond to the C-Cl σ* which weakens the C=C bond and therefore lowers the frequency. This interaction is not present in the endo double bond and so the frequency is higher (stronger bond). There is really little change in the frequency of the endo double bond on hydrogenation as there is no change in any interactions which effect this bond.

Now for furthur investigation of this phenomenon various groups can be put onto the alkene double bond that will alter the electronic properties of the double bond and thus the stretching frequencies in the molecule. The groups that will be trialled on the double bond will be -OH, and CN.

Here are the Important output frequencies from these molecules:

(OH):

(C=C)= 1822.41cm^-1 (exo, intensity=10.9848), 1760.71cm^-1 (endo, intensity=4.3565)

(C-Cl)= 756.597cm^-1 (intensity=13.7618)

(CN):

(C=C)= 1672.6cm^-1 (exo, intensity=3.3154), 1760.69cm^-1 (endo, intensity=5.93)

(C-Cl)=774.743cm^-1 (Intensity=7.6458)

These frequencies and how they change compliment nicely the theory above and what would be expected based on the explanation.

Firstly looking at the -OH adapted molecule. There is an obvious decrease in frequency of the C-Cl stretch down to 756.597cm^-1 from 772.633cm^-1. Since -OH is an electron donating group (Lone pairs) one would expect an increase in electron density in the exo double bond and then also in the C-Cl σ* orbital which would weaken the bond and thence lead to a decrease in frequency. Also the Exo C=C double bond has increased in frequency to 1822.41cm^-1 from 1740.77cm^-1. This is due to the increase of electron density on the double bond and so strengthening it and therefore increasing the frequency

Next looking at the -CN adapted molecule. Firstly looking at the C-Cl stretching frequency. The frequency has gone up from 772.633 to 774.743cm^-1. This increase in frequency is due to an increase in C-Cl bond strength. The electron withdrawing CN groups remove electon density from the exo п-orbital system and thus remove electron density that would have been donated into the C-Cl σ* orbital.

This effect can also be seen reflected in the exo C=C double bond frequency which has gone down to 1672.6cm^-1 from 1740.77cm^-1. Electron density withdrawn from the double bond has weakened it and caused the frequency to go down.

Structure based mini Project using DFT based Molecular Orbital methods

In this part of this Module an experiment is going to ran in which a reaction is looked at that can product two different isomers. Computational spectroscopic methods will be used along with conventional spectroscopic methods data in order to investigate how it might be possible to distinguish between the two isomers. Specifically the GIAO method ¹³C NMR calculations will be ran and compared to spectroscopic data in order to show that it is possible to distinguish between the isomers using this combination of techniques. Other possible suggestions about how one might go about distinguishing two isomers will also be looked into. Optical Rotations and IR can also be calculated and looked at to see if they could help distinguish the isomers.

All this is done using DFT (Density Functional Theory). DFT describes an interacting system of fermions (electrons in this case) not by it's many body wave function but actually by it's density. The system depends only on three co-ordinate x,y and z rather then 3N (N=number of electrons) degrees of freedom. In DFT the particle density is the main variable and in theory the particle density can be used in order to calculate the ground state wavefunction. Since the wavefunction is a functional of the density then any observable property (energy) can be found by operating on this wavefunction which is a functional of density. If one can minimise the energy then one can find the ground state density and other ground state properties.

Initially a suggested reaction was investigated in a preliminary experiment to trial the calculations that will be ran and to get a general feel for the output data. This will be written up first and the procedure explained. However a much more thorough analysis of the numbers and computational outputs will be done in the found literature experiment, NOT in this preliminary work. The preliminary experiment chosen was"Click Chemistry". The idea of this reaction type is to use fast 1,3-dipolar cycloadditions under catalytic conditions (e.g. Cu(I) or Ru(II)) to form molecules. These reactions are easy and also reliable and stereoselective. The specfic reaction that will be studied in this case is seen below: (note that Cu(I) catalysts usually result in isomer A whereas Ru(II) catalysts result in the primarily isomer B). The reason for this can be determined by examining the catalytic cycle and its mechanism for the reaction.

Initially in the Ru(II) catalyst case there is an oxidative addition of the azide nucleophilically. After this there is additon of the internally bound alkyne, futhur reaction takes place to form a six-membered ruthenacycle and then product B is reductively eliminated.

However in the Cu(I) case the alkyne is initially deprotonated. This then terminally binds (unlike in the above exmaple) to the Cu(I) (oxidation). The reaction proceeds and the product is again reductively eliminated. The difference between the two mechanisms that results in the two different isomers (A or B) is the difference in alkyne binding.

non-catalysed Click reaction mechanism which is no good ( plain 1,3-dipolarcycloaddition) but gives an idea of the overall reaction. Note also thatthe alignment in the mechanism would result in Isomer A and would have flip one of the reactants to get the B Isomer.

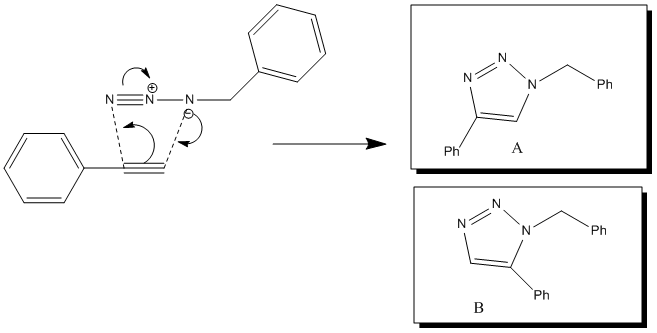
These reactions can be also used in such applciations as biomolecular labelling. Interestingly in order to do this, since copper catalysts are toxic and hence incompatible with living systems strained difluorinated cyclooctynes (DIFO) are used and react quickly with the azides in living cells.

The first isomer that was considered was the isomer A (Click A). Initially an MM2 calculation was ran after drawing the molecule in ChemBio 3D and a lowest energy conformer found. This was then imported into gaussview and a PM3 and then DFT optimisation calculation ran on the molecule. In the DFT optimisation this time a different method was used to b3lyp which was mpw1pw91. Also the basis set was changed slightly from 6-31g(d) to 6-31(d,p) and also note that the maxcycles was set to 25 i.e. the maximum number of optimisation steps that could be ran is 25. The optimisation script for this part was then:

"# mpw1pw91/6-31(d,p) opt(maxcycle=25)"

Nb:important that maxcycles=25 is immediately preceeded by opt script

This calculation was submited to scan but then came back with, at the end of the script, Error termination request processed by link 9999. This simply means that the maxcycles were reached before a minimum energy was converged to. The file was opened with intermediate geometries and the graph of total energy vs. optimisation step number was viewed. This was simply to check that the energy wasn't simply oscillating bewteen each step (this can happen) and so would render increasing the number of maximum steps pointless. However this was not the case this time and so the file was resubmitted to scan for a maxcycles of 45steps. This did converge to an optimised geometry and so now could be furthur analysed.

Futhur analysis will be to submit for an IR analysis and ¹³C NMR analysis in this case since these are the methods that could potentially be used to distinguish the two isomers. It will not be submited for an optical rotation analysis because the molecule contains no chiral centres in either isomers. Submission of this calculation would not only be useless but also a waste of computational time.

The NMR(¹³C) and IR were submitted to scan for analysis using the following scripts:

NMR: "# mpw1pw91/6-31(d,p) NMR scrf(cpcm,solvent=chloroform)"

IR: "# b3lyp/6-31G(d,p) opt freq"

These jobs completed as expected and thus now can be analysed. However first the exact same procedure must be completed but for the the second isomer b (Click B). This time the DFT optimisation did converge on 25cycles, and so then could be submitted to scan for the NMR and IR analysis without furthur optimisation.

Before any analysis is done here are the Jmols for the final optimised structures:

JMol 3D coordinates for Click B after DFT optimisation

Firstly the ¹³NMR will be analysed. An interesting point to notice in the above Jmol is the fact that in click B the conjugated ring systems, built up of the triazole and phenyl system, have actually been twisted off planar from each other (found in Chembio 3D to have a torsional angle of 53.8degrees). This is due to the steric influence of both the benzyl and phenyl group being close to together and so it is actually overall favourable to do this. However in the initial MM2 minimisation this was not the case. This shows a limitation of the MM2 method. The method clearly assigns a high priority to keeping the "conjugated" system by assigning it a high force constant, and thus twisting it off planar would be highly unfavourable in this case. However when looking at the Molecular orbital approach to optimisation the conjugated system is looked at in a less "black and white" manor (i.e. conjugated is conjugated) and the orbital overlaps and what that actually results in is considered (i.e. it can consider more of a spectrum of interaction). This means it does a better job of balancing the sterics of the system to the favourability of electron delocalisation. This effect is not seen in Click A where the conjugated system is maintained as a result of the phenyl and benzyl groups being on the opposite sides of the triazole ring to each other. How this difference between the two molecules manifests will be seen in the NMR next and this subtle difference found by DFT optimisation is actually important in distinguishing the molecules spectroscopically.

NMR analysis-Click Chemistry

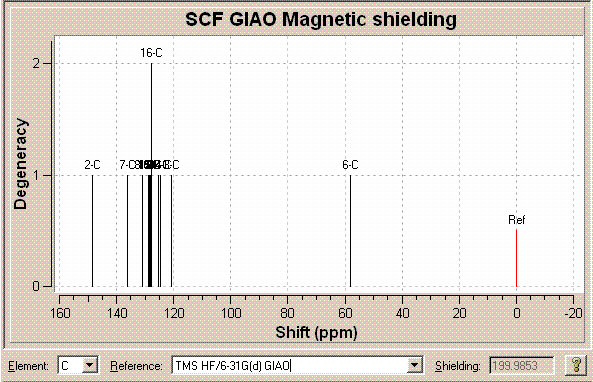
This is the most important technique, I think, in differentiating between the two isomers. The results for the NMR for the first compound, Click A, can be seen below (the reference used in both cases is: TMS HF/6-31G(d) GIAO) alongside the literature values for the molecule and an NMR image. The NMR data from literature is matched as best as possible with the computed values. When the values are repeated in the literature column this is because either of computational values (or both) could be assigned to the literature value. Also note there are multiple values around 128ppm computationally that are very close together (seen in the table below). These could be encorporated into the chemical shifts of the peaks above it around 128ppm but the journal values give no indication of the integration of the peaks. Here is the data: DOI:10042/to-975

Computated NMR Chemical shifts/ppm (Chloroform)	Literature Experimental NMR Chemical shifts/ppm (Chloroform)
148.387	148.0
136.246	134.6
130.826	130.4
128.962	128.9
128.630	128.64
128.423	128.56
128.379
128.265
128.265
128.043
127.795	127.9
127.77 (double degeneracy)	127.9
125.248	125.5
124.701	125.5
120.674	119.5
58.1232	54.0

Looking at the match between the Literature and computed values is highly impressive. The match is generally extremely good. The only slightly ambiguous area is the 128pppm area as mentioned above but all other peaks away from this messy area have extremely good matches.

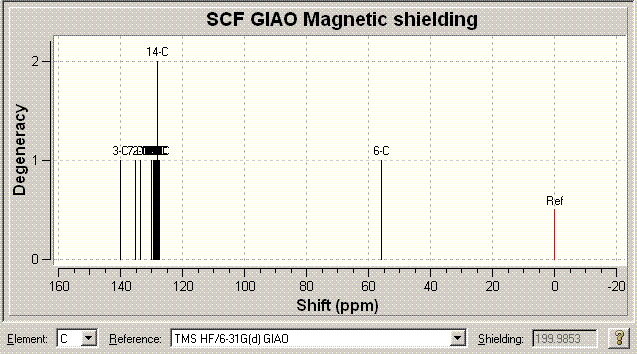
Now lets look at the NMR data for Click B so a comparison between the two isomers can be made: (Again the table has the comparison to literature) DOI:10042/to-974

Computated NMR Chemical shifts/ppm (Chloroform)	Literature Experimental NMR Chemical shifts/ppm (Chloroform)
140.4	138.26
135.014	135.66
133.593	133.34
130.064	133.26
129.359	129.64
128.875	(129.08/128.92)
128.72	(129.08/128.92)
128.612	(129.08/128.92)
128.483	(129.08/128.92)
128.371	(129.08/128.92)
128.242	128.22
128.209	128.22
127.893	127.22
127.511	126.93
55.8468	51.85

The assignments above can be again well correlated with the literature. Another point to make about these spectra that is important to this project is whether the two isomers can be distinguished from looking at the sprectra.

The most important peak I believe in distinguishing the two isomers is that with the highest chemical shift in each case. These are 148.387 (Click A) and 140.4ppm (Click B). The difference in the shift in each case is a subtle and interesting point. In Click A the two benzyl and phenyl groups are far away from each other and so this allows the phenyl ring to maintain a flat relation with respect to the triazole ring and hence a large amount of conjugation. In Click B however the phenyl ring is distorted off of the flat as calculated by (PM3 and DFT) optimisation. This will reduce the amount of conjugation and aromaticity in the system. The Carbon that is effected is that in the triazole ring directly attached to the phenyl ring. In the Click A system since the two rings are in the same plane the aromaticity causes there to be a upfield shift. In Click B because of the fact the two rings are no longer planar (due to sterics) the shift of the C is now no longer as high (less effected by the aromatic effect). This is as stated above as an effect of the molecular orbital calculations tat MM2 doesn't take into account. Using this more advanced model actually results in something subtle between the two isomers that would be recognised in the specta if they were to be taken. Ultimately this shows that the NMR could be calculated computationally initally. Then the reaction could be run and a ¹³C NMR spectrum ran of the products. One could then compare the computed and taken spectrum and know straight away which isomer/isomers were present in the sample. Other peaks that could also be used to distinguish, but given that the peaks are 7.987ppm apart in this case (for the same corresponding carbon) there is no chance of error in the spectra mistaking the two isomers indisinguishable in the laboratory.

Also Running the computational NMR takes very little time (~20mins in this case) to calculate and a normal carbon NMR would also not take long to run. Thus combining these two techniques gives a quick, easy and reliable way to determine which of the two isomers have been made (or in what proportion they have been made).

Another important point to note is that the predicted proton NMR did not match the data well at all but this is not worth writing a section on. The ¹H NMR was not suspected to be useful anyway as mentioned on the wiki page "The method should work for other nuclei (except hydrogen, which requires much greater accuracies to be really useful).",]]

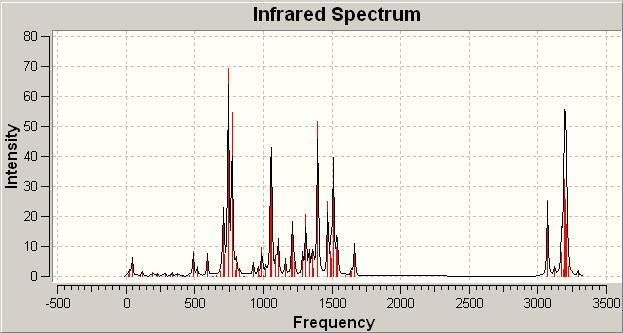
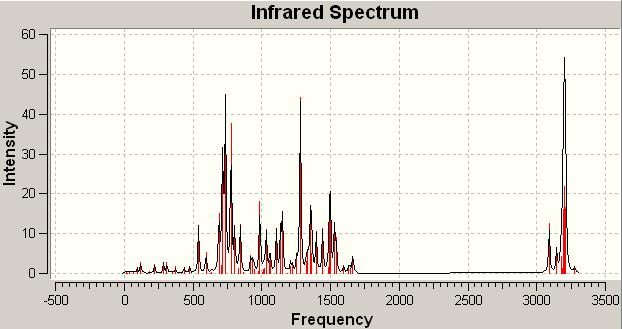
IR analysis of the "Click Chemistry Isomers"

A Frequency analysis of the two isomers was ran. One would expect that there won't really be any difference between the two spectra. This is because the molecules contain very much the same bonds and so hence would have similar vibrations present. However they were run anyway just to see if there is any difference between the two that could not be predicted. e.g. if a particular stretch (similar in which bonds are vibrating) in one isomer lead to a large dipole change and in the other a small dipole change the peak would be more intense in one than the other leading to a difference in the appearance of the spectra.

The spectra can be seen below:

Click A IR spectrum DOI:10042/to-1002

Click B IR spectrum DOI:10042/to-1001

On examination there is very little difference between the two spectra. In some areas there are more intense signals than others but this is nowhere near as useful or conclusive as the ¹³C NMR analysis above. The subtleties between the spectra would be difficult to spot in a laboratory spectrum. Thus as suspected overall the IR analysis if these two isomers is not particularly useful. From these calculations however the free energies could be found:

Click A: -743.467242 Hartrees

Click B: -743.461499 Hartrees

This shows click A is more stable than click B by 3.6037kcalmol^-1 Note conversion which is interesting. This is a fairly significant difference between the two. This is however quite meaningless in determining which one is formed because the reaction is catalysed as to choose the wanted isomer.

This preliminary has shown that in this case ¹³C NMR would be a simple and easy way to tell what isomer one had made in this reaction if one could compute the specta in this simple manor and compare the two. It has also been good practise.

Now this has been done the chosen literature project will now be investigated.

Project-Structural reassignment of the major isomer from the Diels Alder reaction of acryloyl chloride and 4,5,6,6a-tetrahydropentlene

In this project a reaction will be studied that involves using the computational techniques learnt during the preliminary project previous to this as well as the exercises previous to that.

The reaction studied was found in literature and involves studying a Diels-Alder cycloaddition type reaction. The reaction scheme as well as the desciption of the purpose, consequences and problem with the reaction can be seen laid out below:

This is the reaction scheme which was carried out in order to create product 3 primarily for the purpose of studying carbocations and not the direct hydrocarbons themselves.

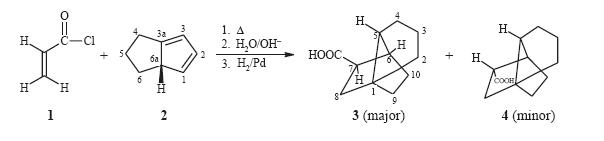
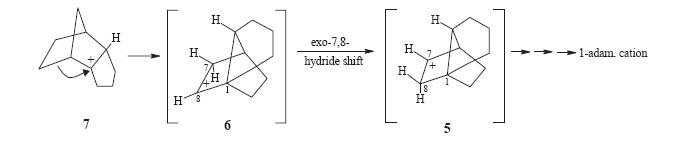
The reason for studying this is that "Cation 5 (see below) was expected to be a key structure in the overall rearrangement of the tetrahydrodicyclopentadiene skeleton into adamantane" and this was being studied (reaction scheme below). If cation 5 could be generated from a suitable precursor then one would expect this to convert into the 1-adamantyl cation. If 6 is formed then one may expected this to proceed backwards to forming 7 (below).

This cation 5 can be formed from both carboxylic acids (3 and 4) on treatment with superacid SbF₅/SO₂ClF which is then expected to convert into the 1-adamantyl cation. Since 3 and 4

were expected to be the products of the Diels-Alder (cycloaddition: _π4_s+_π2_s) reaction to generate the cation 5 one would expect to carry out the Diels-Alder reaction and then simply treat

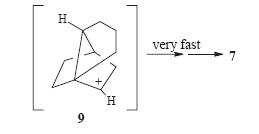
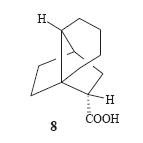
this with superacid. This would then proceed to the single 1-adamantyl cation. However on following this procedure the group found that in fact two cations were present in the mixture. One was the expected forward reaciton 1-adamantylcation but the second was infact the major cation 7. This meant that obviously the products of the Diels-Alder were not as expected and so generated different cations to expected. Analysis of the products of the Diels-alder reaction by NMR (HETCOR, COSY, HMBC and NOESY) lead them to believe that indeed the product 4 was correct but the product 3 was actually product 8(see right). This is out of out of 8 possible adducts of this Diels-alder reaction (carboxylic acid at four different carbons and in each position either endo or exo). This product, 8,can then proceed to to cation 7 via cation 9 (see left).

This then explains the observed reaction results that were found. Another point of interest in this reaction is how these two different products of the Diels-Alder reaction(8 and 4) come about forming. This is simply down to the two different reaction geometries that produce either product 8 and 4. The diene-dieneophile reaction geometries can be seen in the below diagram:

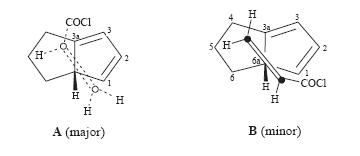
So now spectroscopically how can one think about differentiating between the two isomers. ¹³C NMR I would think to be the best way to differentiate between the two. If in fact one could tell computationally what one would expect the difference between the spectra to be between 3,4 and 8 it would be easy to run an NMR on the Diels-Alder products and tell which of the possible products are present. In this experiment the NMR of 3,4 and 8 will be calculated and compared to literature and each other to tell if one could identify the products easily from a simple 1D NMR and without the need for 2D spectra and more advanaced NOE techniques that were used in journal.

Another technique that could be used to distinguish between the possible three isomers (3,4 and 8) could potentially be used is IR spectroscopy. Although the bonds are really the same (as in the preliminary work) there again might be distinguishing features between the spectra. i.e. even though all would be expected to have similar frequencies there might be potential difference in intensities. This will be looked at because the computational time to run this is short anyway.

Given the molecules have 4 stereocentres each, the optical rotation would expect to change as the carboxyl group is moved around (i.e. the stereocentres are changed). These calculations are fairly time consuming but I am confident there should be significant difference between the molecules in their measurement. Once the values are obtained the usefulness of the technique will be discussed.

Each molecule is drawn in ChemBio3D and then optimised using MM2 to find the lowest energy conformation (this was easy given the rigidity of the molecule) then submitted for a PM3 optimisation and then DFT optimisation. In the literature journal there is a crystal structure of 8 and it does in fact well match the found optimised structure. This is good and shows that the chances are all the molecules have been optimised well and correctly represent the true structures.

dft optimisation method in this project(as given in wiki):

"# mpw1pw91/6-31(d,p) opt(maxcycle=25)"

Molecule 3

Now this optimisation procedure has been run the molecules can be submitted for an NMR calculation. The script used to run this NMR calculation is:

"# mpw1pw91/6-31(d,p) NMR scrf(cpcm,solvent=chloroform)"

Here are the results from the NMR calculation specifically the ¹³C NMR spectrum. Note that the reference used is TMS mPW1PW91/6-31G(d,p) CDCl3 GIAO.

The image included is to show which carbons are assigned to each particular chemical shift. The carboxylic acid carbon will always be assigned as number 11 no matter where about on the molecule it is actually attached. In the table below the carbon number which the shift is assigned to is in brackets next to the chemical shift number.

Molecule 4		Molecule 8		Molecule 3
Real	Calculated	Real	Calculated	Calculated
180.8 (11)	170.766	182.0	171.774 (11)	171.774 (11)
61.1 (7)	61.2286	63.9	65.7297 (6)	59.256 (7)
58.8 (6)	60.1668	63.2	62.7242 (7)	58.813 (6)
52.9 (4)	52.4976	47.0	46.945 (3)	53.4974 (4)
41.25 (1)	43.8845	36.8	38.304 (1)	40.6853 (1)
34.25 (5)	35.2715	36.2	37.9283 (4)	39.152 (5)
32.0 (3)	32.9118	30.8	32.7938 (2)	33.4275 (3)
29.6 (9)	31.3779	29.8	31.4162 (9)	31.8941 (9)
28.7 (10)	30.434	28.2	30.1639 (10)	30.1563 (10)
24.4 (2)	26.0685	27.6	28.7863 (5)	28.9296 (2)
21.3 (8)	23.3548	20.9	23.0257 (8)	23.3073 (8)

The first thing that must be mentioned is how well the two sets of data mach in both cases where the literature values can be found. The only peaks that are off are the carboxylic acid carbon peaks. However this can be roughly be corrected for using the formula δ_corr = 0.96δ_calc + 12.2 . This gives for the three different molecules above corrected chemical shifts of:

4: 176.0336ppm

8: 177.0704ppm

3: 177.1304ppm

This is really good given it is only a simple correction. This now bring the only peaks that were really far off the literature values such that they are now all within 5ppm of the literature. This shows the accuracy of using this technique to distinguish between the molecules. Telling the difference between all the molecules knowing this computational data is easy. Each of the molecules has a good enough difference in Chemical shifts of some of the peaks to distinguish them apart i.e. if a real NMR was ran of the obtained product(s) in the lab and one had this computed data one couold quickly tell which isomers were present saving alot of time using complicated NMR techniques. Molecules 4 can be told apart from 8 and 3 purely on the carboxylic acid peak, and molecules 8 and 3 by the peaks in the region of 60ppm.

Displayed below are the visualised ¹³C spectra for the molecules:

NMR Molecule 4 DOI:10042/to-977

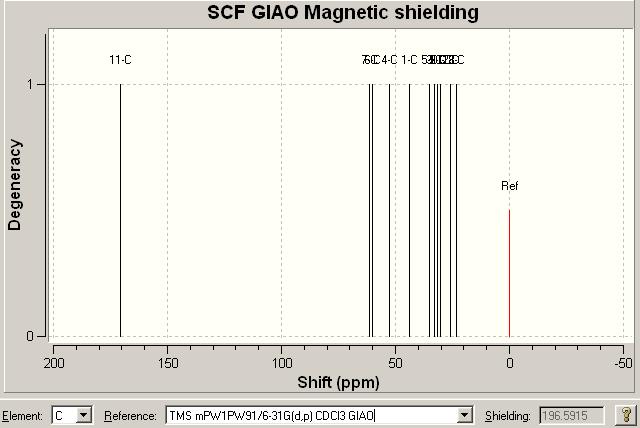
NMR Molecule 8 DOI:10042/to-978

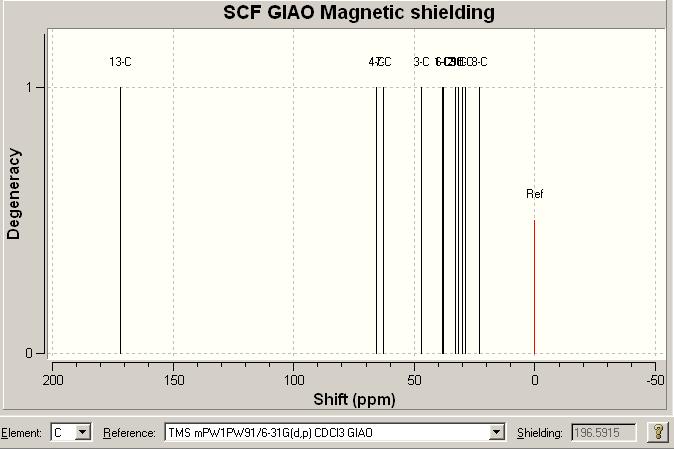
NMR Molecule 3 DOI:10042/to-976

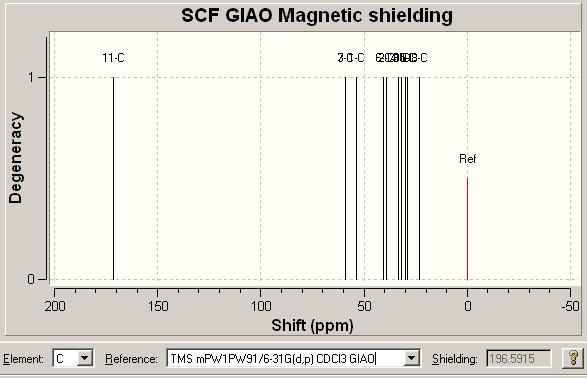
The next thing to look at is the IR spectra of the compounds to see if one could distinguish the molecules apart using this method easily (the script used in order to run the spectra is "# mpw1pw91/6-31(d,p) freq"):

IR Molecule 8 DOI:10042/to-1000

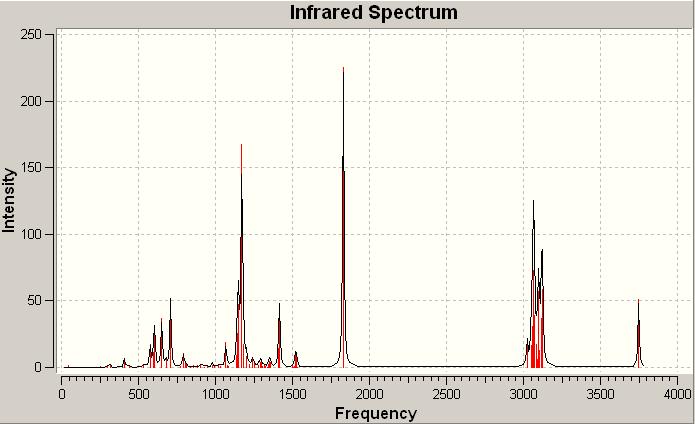
IR Molecule 4 DOI:10042/to-999

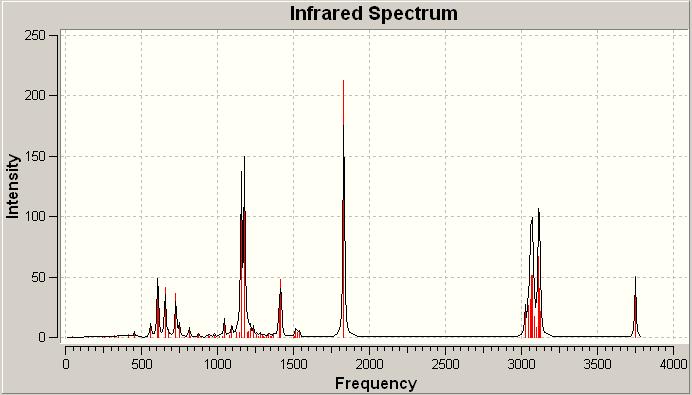
IR Molecule 3 DOI:10042/to-998

Comparing the above spectra the same situation is found as in preliminary experiment. They are all very similar in the position of the peaks. In some places the peaks have slightly different intenisty on close inspection but realistically in a lab the ability to distinguish between the three real spectra would be difficult. Thus this method really wouldn't be used to distinguish between the three molecules.

The next thing to look at will be the optical rotation calculations of the molecules and whether they can be used to distinguish the molecules:

Optical Rotation

Another technique that will be useful to distinguish the isomers might be optical rotation. The molecules all have four stereocentres so will have a possible 16 diastereoisomers. However any changes will results in an overall change in optical rotation measurement and so one only really need to see the overall effect of changing the stereocentres on this measurement. The results of the calculations are as follows:

molecule 8: 60.03 degrees DOI:10042/to-996

molecule 4: -40.06 degrees DOI:10042/to-997

molecule 3: -61.35 degrees (Would not allow result to be published to D-Space?)

This is again conclusive and shows that if one was to isolate or create one of the molecules one could easily tell the difference using an optical rotation measurement. I couldn't find any optical rotation measurements to compare with but if indeed they are close to the calculated values one could easily distinguish between the molecules (i.e. there is a big enough difference between all of them to distinguish under laboratory conditions). The flaws with this is however that a mixture of the molecules would make it difficult to determine which were present overall in the mixture thus rendering the computed information pointless. Also the calculation time for this measurement is quite long ~12hours.

Overall however I would say that the ¹³C NMR is the best technique. This is simply because optical rotation calculations are far more time consuming (computationally expensive) when compared to the NMR calculation and also is more difficult. In this project's case the NMR for each was around ~15mins whereas the OR calcualations in each case were around ~12hours. This makes the NMR in this case (given also that it can indeed distinguish easily between the molecules) the preferential calculation to run.

This experiment has shown that computational techniques can be extremely useful in determining properties of a system and identification of molecules. In identification of the molecules it has shown that computational techniques can help quickly distinguish between prodcuts of a reaction by combining with laboratory spectroscopic techniques. In the process of doing this a lot of painstaking time can be saved. e.g. in the last project in order to determine between the molecules many NMR related techniques were run. If however one simply computed the ¹³C NMR spectra for possible products and then ran a true spectrum and compared, the true product could be easily and quickly identified.

Mechanistic explanation of formed isomers

The mechanism of the initial Diels-Alder reaction is shown at the start of this section. Is there any reason why it is that the two formed isomers are actually 8 and 4? Since the reaction is a cycloaddition reaction the reason for the formed isomers is likely to involve an orbital arguement.

It can be explained why it is that the endo forms are prefered over the exo forms using the same arguement as in the dimerisation of cyclopentadiene. Secondary orbital interactions (overlap) presumeably lower the energy of the endo transition state and so this is the most kinetically favourable route. In the knowledge of this it is somewhat strange that the original assignment involved 3 (exo) in the first place.

So can one rationlise why it is that only the attack geometries A (leading to 8) and B (leading to 4) (seen in the above section) are the prefered?

Note that the reference numbers in the following paragraph refer to the numbers seen in the geometry of attack diagrams previously in this section

The techniques in this lab course can actually help explain why. If one runs B3LYP/6-31G optimisation of the diene (2) the diene unit itself is found to be very close to planar. The C3a to C4 bond however is not in this same plane and so leads to an overall curved geometry of the molecule.The C6a hydrogen is on the convex surface of the molecule.

One can also calculate the orbitals for the acrylic dienophile and one would see that the LUMO orbital coefficient is largest on the terminal CH₂ carbon thus leading one to expect the initial bonding to be strongest at this carbon. A and B are the two attack geometries because given the C3a is already slightly sp³ hybridised (4-3a-6a-1 dihedral angle of -162.6 degrees), and to rehybridise fully one would expect the geometry of attack as in B. On the other hand attack from the underside in this same geometry would be unfavourable because the C3a p_z orbital in the HOMO of the molecule is slightly smaller on the underside. Thus sterically and considering the orbital interaction would lead to suggest that the geometry B would prefer an attack from the top (convex) surface.

A recent theoretical study looking at 5methyl-cyclopentadienes (some similarities to diene 2) and the facial selectivity of Diels-Alder reactions with these types of molecules. The group found 20% syn and 80% anti. Using this model the transition state A would be equivalent to the syn attack.

This however is a round about attempt to try and explain the phenomena seen and really in order for myself to investigate what is going on the transition states must be looked at. This comes under Module 3-Experiment 3 in which transition states of reactions will be investigated.