Rep:Mod:ETZ13TS

Introduction

In this study, the mechanisms of two pericyclic reactions, the Cope rearrangement and Diels-Alder (DA) cycloaddition, were investigated using computational methods. Specifically, the analysis of the transition states of the [3,3] sigmatropic rearrangement of 1,5-hexadiene, DA addition of butadiene and ethylene, and DA addition of maleic anhydride and cyclohexa-1,3-diene.

The mechanistic understanding of reaction schemes relies on the detailed knowledge of transition state structures. However, transition structures correspond to the energy maxima in a reaction, and cannot be isolated and observed. Hence computational calculations are an effective method for the prediction and analysis of transition states. Quantum computational methods were adopted using GaussView 5.0 and Gaussian 09W for this study; These included ab initio Hartree-Fock, Density Functional Theory B3LYP, and the semiempirical method, AM1. The calculations were performed on basis sets 3-21G, 6-31G(d) and STO-3G, respectively. Three optimisation algorithms were employed for the determination of the transition structures; The Berny Algorithm, Frozen Coordinate Method, and QST2 method.

Cope Rearrangement of 1,5-hexadiene

Computational Methods

The ab initio Hartree Fock (HF) method solves for the wavefunction and energy of a system with a few significant approximations to the all-electron Schrodinger equation. Firstly the Born Oppenheimer approximation assumes that the nuclei are frozen with respect to electron movement. Secondly it assumes that each electron behaves independently and moves in a repulsion field produced by the sum of all the other electrons in the system. Thirdly it assumes that the total wavefunction of the electrons is given by a single Slater determinant of the individual spin orbitals, ensuring the antisymmetric property of the wavefunction. Each spin orbital consists of one electron and is a product of the molecular orbital and a spin function. The molecular orbitals consist of a linear combination of atomic orbitals (LCAO), which depend on the basis set used for the approximation. Electron-electron exchange is accounted for by the use of the single Slater determinant for the wavefunction, but electron-electron correlation is not considered. Therefore, HF approximations tend to overestimate the total energy of the system, which may also result in shorter bond length predictions.

Nf710 (talk) 23:08, 10 February 2016 (UTC)This is a brilliant understanding of HF you have covered all of the basic points very well. very well written. its a mean field of potential.

Density Functional Theory (DFT) contrasts from ab initio HF approximations by expressing the total energy in terms of a functional of electron charge density instead of the many electron wavefunctions. The total energy functional consists of a Kohn-Sham kinetic energy, electron nuclear attractive energy, electron electron repulsive energy and the exchange correlation energy functional. The Kohn Sham equation is a pseudo Schrodinger equation which resembles the HF equation except that it uses a classical method for electron electron repulsions. Both electron electron correlation and exchange are accounted for by the exchange correlation energy functional. Hence the accuracy of DFT depends critically on the exchange correlation energy functional. B3LYP is a hybrid functional which involves Becke's three parameter functional and a fraction of the non local electron electron Hartree Fock exchange energy functional and the Lee Young Parr correlation functional.

Nf710 (talk) 23:08, 10 February 2016 (UTC) Again brilliant understanding

The basis set represents the mathematical approximations for the shape of the molecular orbitals. Gaussian functions are usually used for the expansion of molecular orbitals. In this study split-valence sets are used, where each valence shell orbital is calculated as the sum of two Slater-type orbitals (STO) multiplied by a proportionality coefficient, d. The Slater Orbitals are a function of radius (r) and zeta (ζ), which determines the diffuseness of the orbital. The inner-shell electrons are defined by a single Slater Orbital. These basis sets are expressed as K-LMG where K, L and M are integers. The basis sets used are K=3/6, L=2/3, and M=1 ie., 3-21G or 6-31G*. In the 3-21G basis set, the inner shell orbital is the sum of three Gaussian functions. The valence orbital, split into the first and second STO, is defined with two and one gaussian functions respectively. The same methodology applies for 6-31G*, where the asterisk accounts for the polarization effect for 'p' orbitals by adding 'd' character.

Background

Figure 1. Cope rearrangement

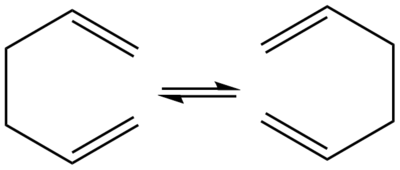
The Cope rearrangement of 1,5-hexadiene is a [3,3]-sigmatropic rearrangement. A sigmatropic rearrangement refers to a pericyclic reaction where a σ bond is formed and another σ bond is broken. [3,3] refers to the number of carbons between the formed and broken σ bonds. Pericyclic reactions must follow Woodward-Hoffman rules, which state that the sum of the number of (4q + 2)_s and (4r)_a components must be odd to be thermally allowed. 'S' and 'a' are acronyms for suprafacial and antarafacial respectively. However if it is an even number it is photochemically allowed.

The Cope rearrangement can take place through both chair and boat transition states as they both follow the Woodward-Hoffman rules. For example, the chair transition structure has 3 components, _π2_a, _π2_s, _σ2_a, which add up to 1. The reaction has an equilibrium constant K = 1 as the reactant and product is the same.

Previously, a stepwise mechanism involving a diradical intermediate was proposed. However the pericyclic mechanism is now widely accepted. The debate about the contrasting mechanisms arose from the small energy differences between the diradical intermediate and transition state amid a lack of experimental data and conflicting theoretical calculations.

Nf710 (talk) 09:43, 11 February 2016 (UTC) good mechanistic understanding

Optimization the Reactants and Products

Optimization of 1,5-hexadiene Conformers

Multiple conformers of 1,5-hexadiene were prepared with GaussView 5.0 and Gaussian 09W. Initially the structures were drawn and cleaned with GaussView. These structures were then optimized using the HF/3-21G level of theory using the Berny Algorithm (default) and are presented in the table below, along with the corresponding point group and energy. The Berny Algorithm is an eigenvector following algorithm, where the eigenvectors are obtained through calculating the second derivative of the potential energy with respect to the nuclear displacement aka. force constant (from the Hessian).

The point group was then obtained through the symmetrize function. The conformer names correspond to the structures provided in Appendix 1 of the script.

Conformer	Structure	HF/3-21G Calculation	Energy / hartrees	Point Group
Anti4			-231.69097	C1
Gauche4			-231.69153	C2
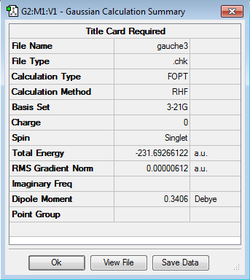
Gauche3			-231.69266	C1
Anti2			-231.69254	Ci

Figure 2. Labelled conformer of 1,5-cyclohexadiene

By definition, the 4 central carbon atoms (C₂-C₃-C₄-C₅) of the anti conformers have a dihedral angle of 180°, whereas the gauche conformers have that of 60°. The factors that differentiate the specific anti / gauche conformers from each other are the dihedral angles of C₁-C₂-C₃-C₄ and C₃-C₄-C₅-C₆. The computed conformer energies are in agreement with the values provided in Appendix 1. All the conformers adopt A^1,3 eclipsed conformations at both of their double bonds. This conformation is preferred over the A^1,2 eclipsed conformation electronically due to a good alignment of the σ_C-H/C and the π*_C=C orbitals (θ ~ 0°). This results in 2 hyperconjugation interactions.

As shown, the anti2 has a lower energy than anti4 conformer and thus is more stable. This is because there is a destabilizing A^1,3 strain at one of the double bonds of the anti2 conformer. Generally the gauche conformer is expected to be more unstable than the anti conformer due to unfavorable steric (gauche) interactions between the two alkenyl groups. However gauche3 is shown to be the most stable. This arises due to an in-phase overlapping π clouds in the HOMO and the presence of CH/π hydrogen bonds. For the same reason, the gauche3 is more stable than the gauche4 conformer. A Jmol is provided here.

Figure 3. Overlap of π electron clouds in HOMO

Nf710 (talk) 09:53, 11 February 2016 (UTC) excellent use of the orbitals and jmols to show the energy ordering. and good explanation

Comparison of different levels of theory

The anti2 conformer was further optimized using B3LYP/6-31G(d) as shown below.

Conformer	Structure	B3LYP/6-31G(d) Calculation	Energy / hartrees	Point Group
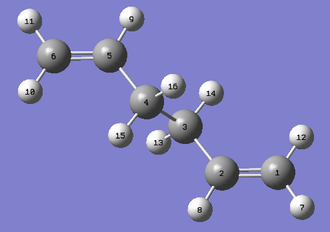
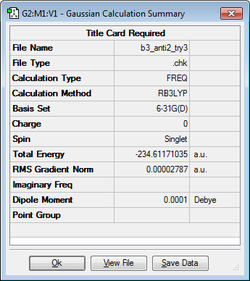
Anti2			-231.61171	Ci

As different basis sets and methods are used, the difference in energies cannot be compared. Hence comparisons must be made with regards to the overall geometry. Comparison of the model predictions and experimentally measured bond lengths and angles clearly show that the DFT calculations are more accurate. The molecular orbital calculation using HF/3-21G gives both shorter bond lengths and smaller dihedral angles owing to the neglect of electron-electron interaction energy. The exception is the C₃-C₄ bond length, which is longer due to the underestimation of the dihedral angle. Note that the bond lengths are symmetrical about the centre of the molecule and so only half have been included.

Bond Lengths
Atoms	B3LYP/6-31G(d) / Å	HF/3-21G / Å	Experimental / Å
C1-C2	1.33350	1.31615	1.340 ± 0.003
C2-C3	1.50420	1.50893	1.508 ± 0.012
C3-C4	1.54816	1.55280	1.538 ± 0.027

Dihedral Angle
Atoms	B3LYP/6-31G(d) / °	HF/3-21G / °	Experimental / °
C1-C2-C3-C4	118.58635	114.66373	120
C2-C3-C4-C5	180.00000	179.99970	168

The frequency is proportional to the square root of the eigenvalue from the diagonal matrix of the Hessian (Harmonic oscillator equation), where the Hessian is calculated from the second order derivatives of energy. A negative sign in the second order derivative implies an energy maximum. Hence a negative eigenvalue will give an imaginary frequency, which is represented with a negative number with Gaussian. As a result the presence of negative frequencies indicates that the structure has not been optimized to its minima. A frequency calculation of the anti2 conformer of 1,5-hexadiene at the B3LYP/6-31G level of theory revealed that all the vibrational modes have a positive frequency, and so a minima has been achieved.

Nf710 (talk) 11:29, 11 February 2016 (UTC) this is a good explanation however you could have included an explanation

Thermochemistry

The thermochemical properties of the anti2 conformer at 0 K and 298 K are presented in the table below. The 0 K calculation is as expected where the thermal energy is 0. Moreover the thermal energy is shown to be an insignificant factor in the determination of the energy of the structure at 298 K.

	Calculation at 298 K / Hartrees	Calculation at 0 K / Hartrees
Sum of electronic and zero-point energies	-234.469215	-234.469203
Sum of electronic and thermal energies	-234.461867	-234.469203
Sum of electronic and thermal enthalpies	-234.460923	-234.469203
Sum of electronic and thermal free energies	-234.500799	-234.469203

Nf710 (talk) 11:41, 11 February 2016 (UTC) Well done for doing it at different temperaturs however you could have done one at a higher temp as 0K is obviously all going to be the same

Optimization of Chair and Boat Transition Structures

Optimization of Chair TS with Guess Method

The Guess method involves creating a "guess" structure which is energetically similar to the transition state and then finding the energy maxima using the Berny Algorithm which was described previously. This method is heavily dependent on the initial "guess" structure which needs to be as close to the transition structure as possible. Hence the allyl fragments are first optimised at the HF/3-21G level of theory.

Allyl Fragment Structure	HF/3-21G Calculation	Energy / hartrees	Point Group
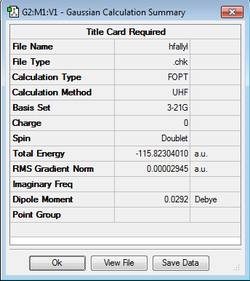
		-115.82304	C2V

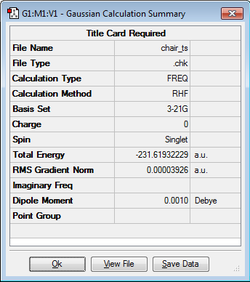
A "guess" chair transition state is then made, comprimising of two allyl fragments with the terminal carbons 2.2 Å apart. This structure was then optimized to the transition state using the Berny algorithm, and through calculating the force constants once. The keyword opt=noeigen is used to prevent Gaussian from crashing when an imaginary frequency is calculated. To verify that a transition state is found, the vibrational spectrum must yield one imaginary frequency, meaning that the energy is a maximum in one direction and a minimum in the other orthogonal directions. As shown below, a single imaginary frequency of -818 cm^-1 was found, confirming the transition state.

Chair TS Structure	HF/3-21G Calculation	Imaginary Frequency (-817.91cm-1)	Energy / Hartrees
			-231.61932

Optimization of Chair TS with the Frozen Method

Utilizing the redundant coordinate editor, specific potential energy surfaces can be scanned with Gaussian. Firstly, by freezing the terminal carbons of the allyl fragments to be 2.2 Å apart, the lowest energy configuration of the allyl fragments can be found at the HF/3-21G level of theory. The TS is then computed with the Berny algorithm but limiting the direction of movement by keeping the allyl fragments fixed but changing the distance between them. This is achieved through setting the terminal carbons of the allyl fragments as a "derivative".

As shown below, a single negative frequency is found. As described before, this indicates the presence of the transition state.

Chair TS Structure	HF/3-21G Calculation	Imaginary Frequency (-817.89cm-1)	Energy / hartrees
			-231.61932

Comparison of Guess and Frozen Coordinates method

The energies of the Guess and Frozen Coordinates methods are the same to 6 decimal points (-231.61932229 and -231.61932233 Hartrees, respectively). The discrepancy of further decimal points arises from error originating from the step size of the algorithm. Similarly, the imaginary frequencies are equal to 1 decimal point (-817.91 and -817.89cm^-1 (Gaussian has an accuracy to the nearest integer). Furthermore, the bond lengths are the same to 3 decimal points as shown below (Gaussian has an accuracy to the nearest 2 decimal points). Hence both methods are perfectly viable for calculating the transition structure .

	Bond forming bond length / Å	Bond breaking bond length / Å
TS from Guess method	2.02039	1.38928
TS from Redundant coordinates method	2.02071	1.38930

Optimization to Boat TS utilizing QST2

The QST2 method is another method to find the transition state, where the structures of the reactant and product are specified. Clearly this method is more advantageous as a 'guess' transition structure is not required (Note that QST3 uses a guess transition structure). QST2 utilizes the Synchronous Transit-Guided Quasi-Newton (SQTN) Method. Firstly it uses a linear synchronous transit approach, where it assumes that the position of the atom in the transition state lies halfway between the position of the reactant and that of the product. Once at the geometry, it uses an eigenvector following algorithm to find the energy maxima.

Reactant	Product

Figure 4. Failed QST2 Transition Structure

The first attempt to search for the transition state using QST2 was made at the HF/3-21G level of theory. The labelled anti2 conformers used are shown above. However as shown in Figure 4., the transition state produced is clearly wrong. This is believed to be due to significant differences in the geometries between the reactant/product and the transition structure. As a result, the midpoints of the two geometries do not accurately reflect the transition state structure so the eigenvector following algorithm finds the wrong maxima. Hence it is important to note that QST2 can fail when the geometries of the reactants and products are far from the transition state.

The anti2 conformer was then twisted to form a pseudo boat geometry to better reflect the boat-like transition state, as shown below.

Reactant	Product

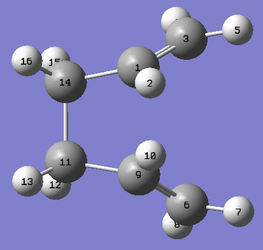
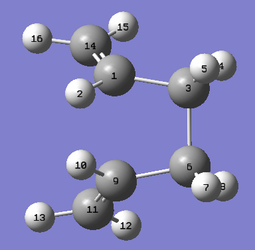
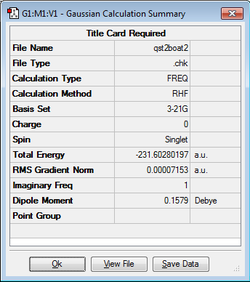
Using the same methodology, the transition state was then calculated. A single vibrational frequency of -840 cm^-1 and a corresponding energy, -231.602802 Hartrees was found. The boat-like transition state energy is slightly higher than that calculated for the chair-like transition state and so is less stable.

Boat TS Structure	HF/3-21G Calculation	Imaginary Frequency (-839.96cm-1)	Energy / hartrees
			-231.60280

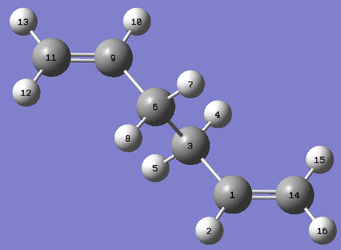
Intrinsic Reaction Coordinate of Chair TS

Figure 5. Total Energy along IRC of the chair transition structure of 1,5-hexadiene

Figure 6. RMS Gradient Norm along IRC of the chair transition structure of 1,5-hexadiene

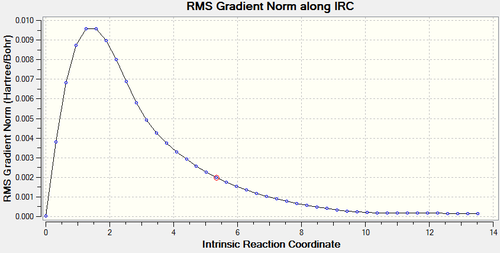
The Intrinsic Reaction Coordinate (IRC) utilizes the Hessian-based Predictor integrator algorithm (HPC) to calculate the forward and backward reaction paths from the transition state structure. In addition, it provides geometries of the structures along the reaction path, defined by the number of points, N. An IRC was run for the chair transition state for 1,5-hexadiene at the HF/3-21G level of theory. The force constants were calculated at each step to ensure an optimum reaction path.

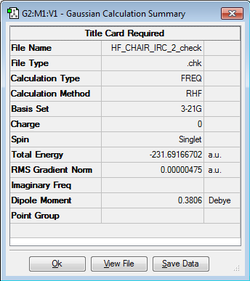
As the reactant and product are the same, the following calculation only calculated the IRC in one direction with N = 50. As shown in Figure 5. the reaction terminated when N = 44 with an energy of -231.691579 Hartrees. Furthermore, Figure 6. shows that this corresponds to the region where the RMS Gradient Norm approaches zero showing that the energy no longer changes. An optimization for the structure was then run at the HF/3-21G level of theory to ensure the minimum energy structure was found. This was revealed to be the gauche2 conformer shown in the appendix of the script. Note that there was a slight optimization due to the IRC having a higher threshold of defining the minimum energy structure.

Chair TS Structure	HF/3-21G Calculation	Energy / hartrees
		-231.691667

Nf710 (talk) 11:45, 11 February 2016 (UTC) Good understanding of the IRC mechanism

Optimization of chair and boat TS with B3LYP/6-31G(d)

The chair and boat transition structures of 1,5-hexadiene were then reoptimized with the B3LYP/6-31G(d) level of theory. As before this was achieved with the Berny algorithm. The boat and chair transition structures had imaginary frequencies of -530.36 and -565.54cm^-1 respectively, indicating the transition structure has been found.

Boat Transition Structure	B3LYP/6-31G(d) Calculation	Imaginary Frequency (-530.36cm-1)	Energy / Hartrees
			-234.543093

Chair Transition Structure	B3LYP/6-31G(d) Calculation	Imaginary Frequency (-565.54cm-1)	Energy / Hartrees
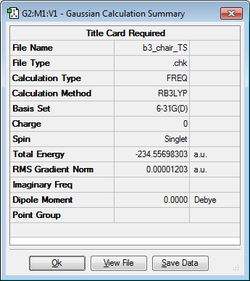
			-234.556983

Activation Energies

The thermochemical data obtained from the frequency calculations of the anti2 conformer, boat TS using HF/3-21G and B3LYP/6-31G levels of theory are presented below. As previously mentioned the chair transition structure provides a lower energy pathway and hence is favoured. Furthermore both activation barriers decrease with temperature. HF/3-21G calculations significantly overestimate the activation energies whereas B3LYP/6-31G(d) slightly underestimate the activation energies. The origin of the discrepancies have been described previously.

Interestingly, although HF/3-21G overestimates the energies by approximately 30%, the bond lengths and dihedral angles are slightly under experimental values. This is assumed to be because electron electron correlation plays a smaller role in the determination of bond lengths than energy.

	HF/3-21G			B3LYP/6-31G(d)
	Electronic Energy / Hartrees	Sum of electronic and zero-point energies at 0K / Hartrees	Sum of electronic and thermal energies at 298.15K / Hartrees	Electronic Energy / Hartrees	Sum of electronic and zero-point energies at 0K / Hartrees	Sum of electronic and thermal energies at 298.15K / Hartrees
Chair TS	-231.619322	-231.466699	-231.461340	-234.556983	-234.414929	-234.409009
Boat TS	-231.602802	-231.450928	-231.445299	-234.543093	-234.402342	-234.396008
Reactant (anti2)	-231.692535	-231.539540	-231.532566	-234.611710	-234.469203	-234.461856

	HF/3-21G at 0K	HF/3-21G at 298.15K	B3LYP/6-31G(d) at 0K	B3LYP/6-31G(d) at 298.15K	Expt. at 0K
ΔE (Chair) / kcal mol-1	45.71	44.69	34.06	33.16	33.5 ± 0.5
ΔE (Boat) / kcal mol-1	55.60	54.76	41.96	41.32	44.7 ± 2.0

Nf710 (talk) 11:54, 11 February 2016 (UTC) Your energies are correct,but you havnte done a geometry comparison and therefore shown that lower basis sets are good at determining geometries. However you have shown excellent grasp of the knowledge of the computational methods used which is impressive.

The Diels Alder Cycloaddition

Background

Diels-Alder

Figure 7. Cis-butadiene and ethylene

Figure 8. Maleic Anhydride and cyclohexa-1,3-diene exo and endo selectivity

The Diels-Alder reaction is a [4+2] cycloaddition. It is a pericyclic reaction involving the concerted formation of two σ bonds to join together two conjugated π systems. The [4+2] refers to the number of π electrons in each component, where 4 represents the diene and 2 the dienophile. The diene is required to adopt an s-cis conformation. Electron withdrawing groups (EWG)/conjugation on the dienophile favour the reaction as it lowers the energy of the LUMO. Similarly, electron releasing groups (ERG) on the diene favour the reaction as it increases the energy of the HOMO. This allows for a better interaction between the HOMO of the diene and the LUMO of the dienophile

The reaction is regioselective, where an ERG group on the diene prefers to be ortho or para to the EWG on the dienophile. This can be deduced from a frontier molecular orbital analysis. It is also stereoselective and follows the Alder Rule, which states that the endo (kinetic) product is preferably formed in irreversible reactions. The endo product is defined where the dienophile substituent faces the diene. This is due to secondary orbital effects between the π systems as well as other effects to be mentioned later. Furthermore it is thermally allowed as a Woodward Hoffman analysis of its components, _π4_s and _π2_s yields a sum of 1 (odd).

In the following sections the Diels-Alder reaction of cis-butadiene with ethylene, and cyclohexa-1,3-diene with maleic anhydride will be examined. The strongly electron withdrawing character of maleic anhydride make the Diels Alder reaction highly favourable.

Previous proposals included a stepwise mechanism but has been since revealed to have a higher activation barrier. Note that this study does not account for the pre- and postchemical processes, including the rotation of trans butadiene to the more stable cis conformer. A recent study revealed that charge transfer facilitates the formation of the cis butadiene conformer as well as the pyramidalization of the reacting carbon centers.

(Good introduction with a new paper. Actually the trans-conformer is the more preferred, by calculations with AM1 and according to the paper you're citing Tam10 (talk) 12:58, 4 February 2016 (UTC))

Computational Background

In the following calculations, the Semi-empirical/Austin Model 1 (AM1) method is used. Semi-empirical methods use Hartree Fock for its framework but include approximations and parameters based on empirical (experimental) data. It uses a minimum basis set (STO-3G) for the occupied orbitals of the valence electrons and considers the core electrons only for their nuclear shielding effect. Furthermore, the AM1 is an extension of the NDDO (Neglect of Differential Diatomic Orbital Overlap) integral approximation by introducing radial Gaussian functions to modify the core-core repulsions. The advantage of the semi-empirical method is its computational efficiency and suitability for large systems. Its disadvantage lies in its limited accuracy which is dependent on experimental data.

Diels Alder Cycloaddition of cis-butadiene and ethylene

Optimization of cis-butadiene and ethylene

Cis-butadiene and ethylene were drawn and cleaned with GaussView. The structures were then optimized at the Semi-Empirical/AM1 level of theory. A further frequency analysis revealed that there were no negative frequencies showing that they were the minimum energy structures.

Molecule	Structure	Semi-Empirical/AM1 Calculation	Energy / Hartrees	Point Group
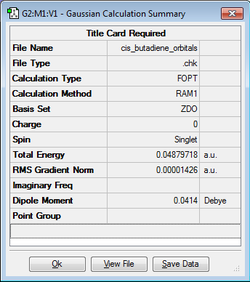
Cis-butadiene			0.04879718	C2v
Ethylene			0.02619027	D2h

(cis-butadiene with a dihedral angle of 0º is not really a minimum. Perform a frequency calculation to confirm this, but sterics from the hydrogens makes a slightly distorted gauche the preferred form Tam10 (talk) 12:58, 4 February 2016 (UTC))

With respect to the plane perpendicular to the central C-C bond, the HOMO of cis-butadiene is antisymmetric, and the LUMO is symmetric. With respect to the plane perpendicular to the C=C bond, the HOMO for ethylene is symmetric, and the LUMO is antisymmetric.

Molecule	HOMO	LUMO
Cis-butadiene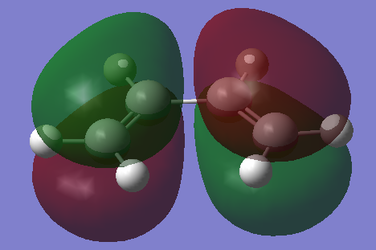
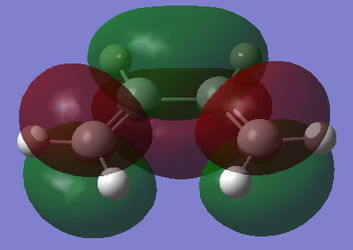
Ethylene

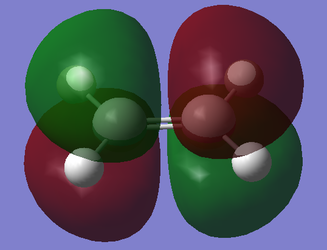Optimization of cis-butadiene and ethylene TS

Despite the ethylene not having an electronegative substituent, it is assumed that this reaction can still proceed as the difference in energy between the HOMO of the diene and the LUMO of the dienophile is only 0.40483 Hartrees. The transition structure of this reaction was found using the Berny Algorithm using the Semi-Empirical/AM1 level of theory. The guess structure consisted of the optimized diene and dienophile with the terminal carbons 2 Å apart, which provided a satisfactory initial Hessian.

(Is 0.40483 Hartrees not quite a lot? Have you compared it to literature? Tam10 (talk) 12:58, 4 February 2016 (UTC))

A lone imaginary frequency of -956.24 cm^-1 was obtained indicating the presence of the transition state, showing the concerted formation of two σ bonds as the bonds are stretched and compressed. The next lowest frequency is 147.24 cm^-1. As previously mentioned, this shows that there is only one energy maxima, corresponding to the imaginary frequency vibration and the rest of the vibrations result in an energy minima. As shown below, the vibration with the frequency 147.24cm^-1 shows a rotation of the dienophile relative to the diene (or vice versa), and does not involve any bond compression or extension which could be regarded as the formation or breakage of bonds.

Structure	Semi-Empirical/AM1 Calculation	Imaginary Frequency (-956.24cm-1)	Energy / Hartrees	Lowest Positive Frequency (147.24cm-1)
			0.11165474

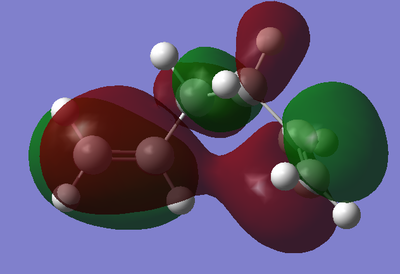
Relative to the plane perpendicular to the central C-C bond of the diene and C=C bond of ethene, the HOMO is antisymmetric and the LUMO is symmetric. The HOMO consists of the addition of the HOMO of cis-butadiene (antisymmetric) and the LUMO of ethylene (antisymmetric). The LUMO consists of the addition of the LUMO of cis-butadiene (symmetric) and the HOMO of ethylene (symmetric). Links to Jmol: HOMO, LUMO

(Nice JMols. If you want, in future, you can set "mo cutoff 0.02" so the same threshold as GaussView is used Tam10 (talk) 12:58, 4 February 2016 (UTC))

HOMO	LUMO

Figure 9. Labelled Transition State diagram

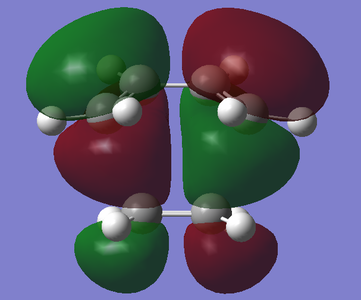
Through the analysis of the bond lengths of the transition state, one can examine the partially forming and breaking of bonds. For reference, the van der Waals radii of carbon is 1.70 Å, Csp³-Csp³ bond lengths are 1.54 Å and C=C double bond lengths are 1.34 Å. In addition, only half of the bond lengths are examined as the transition state has an internal mirror plane (meso).

Twice of the van der Waals radius indicates the minimum distance for two atoms to be non-bonding. As shown, the distance between the two terminal atoms, C₁ and C₃, are within this distance and hence shows a bonding interaction. This indicates the formation of the new σ bond. Simultaneously, the C₁-C₂, C₃-C₄ bond length increases so that the atoms gain sp³ character (as the single bond forms) to facilitate for the new σ bond formations between C₁ and C₃. This also results in the C₄-C₅ bond compression, forming a double bond and the carbons gaining sp² character. Note that this all happens in a concerted fashion.

Atoms	Bond Length / Å
C1-C2	1.38291
C3-C4	1.38186
C4-C5	1.39748
C1-C3	2.11927

Cycloaddition of Maleic Anhydride and Cyclohexa-1,3-diene

Optimization of Maleic Anhydride and Cyclohexa-1,3-diene

Maleic anhydride and cyclohexa-1,3-diene are drawn and cleaned in GaussView and optimised in Gaussian with the Semi-empirical/AM1 level of theory. Further frequency analysis showed no negative frequencies in the IR spectrum indicating that the minimum energy structure has been generated.

Molecule	Structure	Semi-Empirical/AM1 Calculation	Energy / Hartrees	Point Group
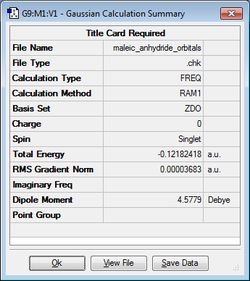
Maleic Anhydride			-0.12182418	C2v
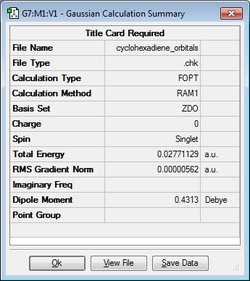
Cyclohexa-1,3-diene			0.02771129	C2

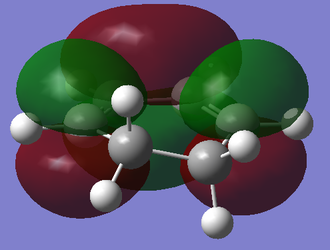
For maleic anhydride, with respect to the plane perpendicular to the C=C bond, the HOMO is symmetric and the LUMO is antisymmetric. For cyclohexa-1,3-diene, with respect to the plane perpendicular to the sp²-sp² single bond, the HOMO is antisymmetric and the LUMO is symmetric.

Molecule	HOMO	LUMO
Maleic Anhydride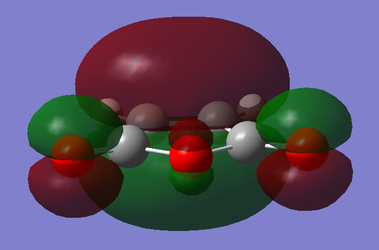
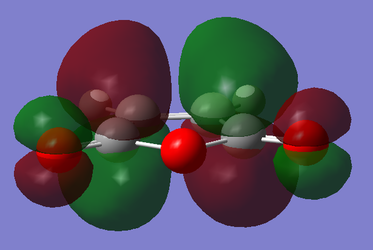
Cyclohexa-1,3-diene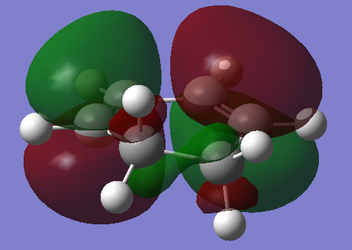

Optimization of Exo Transition State

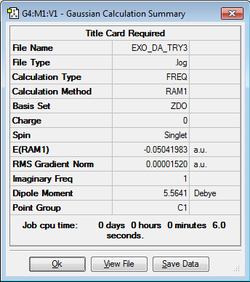
The exo transition state was optimized using the Berny Algorithm at the Semi-empirical/AM1 level of theory. In order to provide a suitable guess structure so that the initial Hessian's eigenvectors can lead to the transition state, the exo product was firstly optimised. This was achieved through drawing and cleaning the exo product, and optimising it at Semi-empirical/AM1 level of theory. The bond lengths between the maleic anhydride and the cyclohexa-1,3-diene fragments were then elongated to 2 Å and the double bond on the cyclohexa-1,3-diene fragment was elongated to 1.45 Å. These chosen lengths were roughly based on the values from the ethene cis-butadiene transition structures. This method was successful as a single imaginary frequency of -812 cm^-1 was found, indicating an energy maxima for the vibration. Furthermore the vibration shows the elongation and compression of the bonds to form the exo product structure.

Structure	Semi-Empirical/AM1 Calculation	Imaginary Frequency (-812.16cm-1)	Energy / Hartrees
			0.11165474

(This looks like the energy of the butadiene-ethene TS... Tam10 (talk) 12:58, 4 February 2016 (UTC))

With respect to the plane perpendicular to the C=C double bond, the HOMO and LUMO are both antisymmetric. Jmol hyperlinks: HOMO, LUMO

HOMO	LUMO

Optimization of Endo Transition State

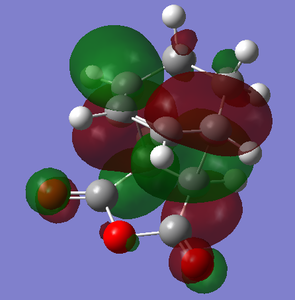
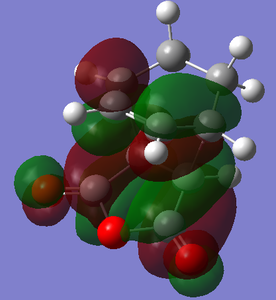
The endo transition state was optimised in a similar fashion as the exo transition state, where the only factor that changes is that the endo product is used. This method succeeds as a single imaginary frequency of -806 cm^-1 is generated. This vibrational mode shows the bond elongation and compression to generate the endo product.

Structure	Semi-Empirical/AM1 Calculation	Imaginary Frequency (-806.43cm-1)	Energy / Hartrees
			-0.16017081

(... and this looks like the maleic anhydride-cyclohexadiene endo adduct energy Tam10 (talk) 12:58, 4 February 2016 (UTC))

With respect to the plane perpendicular to the C=C bond, the HOMO and LUMO are both antisymmetric. Jmol hyperlinks: HOMO, LUMO

HOMO	LUMO

Comparison of the activation energies of the endo and exo TS

Although the endo TS is more sterically crowded than that of the exo TS, the endo TS has a lower energy and so results in the kinetic product. This preference has been coined the endo rule. In general this has been attributed to secondary orbital interactions, greater dispersion forces and a greater electrostatic attraction. The secondary orbital interaction for the endo TS originates from the overlap of the π orbitals of the cyclohexa-1,3-diene with the C=O π orbitals from maleic anhydride.

(I don't think the endo TS is more sterically crowded Tam10 (talk) 12:58, 4 February 2016 (UTC))

Fernández et al. further elucidated this selectivity using the activation strain model, and proposed that the difference arises from the energy required to deform the reactants. For the exo transition state, the oxygen on maleic anhydride and the Csp³-Csp³ on cyclohexa-1,3-diene are repelled due to Pauli repulsion of the O lone pairs and C-H sp³ orbitals, causing a significant deformation. Hence the strain energy required for the deformation is higher for the exo TS than endo TS.

(This conflicts with your previous statements Tam10 (talk) 12:58, 4 February 2016 (UTC))

An analysis of the nodal properties of the HOMO between the -(C=O)-O-(C=O)= fragment and the remainder of the system reveals steric congestion in the exo transition state.

	Semi-empirical/AM1 at 0K	Semi-empirical/AM1 at 298.15K
ΔE Exo TS / kcal mol-1	28.69	28.46
ΔE Endo TS / kcal mol-1	27.82	27.70

	Semi-Empirical/AM1
	Electronic Energy / Hartrees	Sum of electronic and zero-point energies at 0K / Hartrees	Sum of electronic and thermal energies at 298.15K / Hartrees
Exo TS	-0.050420	0.134879	0.144881
Endo TS	-0.051505	0.133494	0.143683
Maleic Anhydride	-0.121824	-0.063346	-0.058192
Cyclohexa-1,3-diene	0.027711	0.152502	0.157726

Comparison of bond lengths of exo and endo TS

Bond	Exo TS / Å	Endo TS / Å
C1-C2	1.397	1.397
C2-C3	1.394	1.393
C3-C4	1.490	1.491
C4-C5	1.522	1.523
C6-C7	2.170	2.162
C7-C8	1.410	1.408
C8-C9	1.488	1.489
C9-O10	1.410	1.409

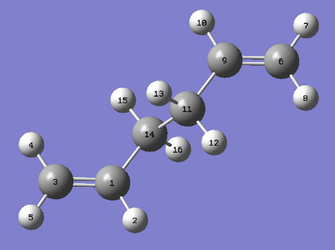
Steric congestion can be observed in the exo transition structure as the C₄-C₉ bond distance (2.95 Å) is smaller than the combined van der Waals radii (3.40 Å). As a result, the exo has a larger interfragment distance C₆-C₇ than that of the endo structure. Although they both are within the combined van der Waals radii which indicate a bonding interaction of in phase orbitals, the endo's distance is smaller indicating a greater orbital overlap and stabilization.

The remaining bonds indicate the extension and compression of bonds as the reactant transitions to the product and vice versa. Furthermore they are similar for both the exo and endo transition structures. Note that only half the bond lengths are used as the transition structures have an internal mirror plane of symmetry (meso).

Labelled Exo TS Diagram	Labelled Endo TS Diagram

Conclusion

The computational study of the Cope rearrangement of 1,5-hexadiene has further confirmed that the reaction proceeds via a concerted pericyclic mechanism instead of a previously debunked theory of the diradical intermediate through an analysis of the transition state. Furthermore, the calculations have revealed that although both the chair and boat transition states are thermally allowed, the chair transition state is energetically favoured. In the meantime, the limitations of the transition state determination algorithms were discussed; the Berny algorithm needs a suitable 'guess' structure, and so the Frozen Coordinate method is a better stepwise alternative. The QST2 method requires the reactant and products to be structurally similar to the transition state. Finally, the calculations have also highlighted the limits of HF theory, showing that the predicted energies are higher than experimental values (36% and 24% for the chair and boat respectively). The high accuracy of the hybrid DFT method using B3LYP/6-31G(d) is also demonstrated.

For the study of the Diels Alder cycloaddition of cis-butadiene with ethylene, further understanding of the orbital interactions was developed. The HOMO and LUMO interactions of the reactants were examined and were related to the formed products. The Berny algorithms limitations were demonstrated again.

Finally for the study of the Diels Alder cycloaddition of maleic anhydride with cyclohexa-1,3-diene, the endo rule was examined. The interactions destabilizing the exo transition state included the strain energy to deform the reactants and the steric congestion of the transition state, which limited the inphase orbital bonding interactions. The interactions stabilizing the endo transition state included secondary orbital effects. The advantages of the Berny Algorithm were shown with this method as it provided a fast and facile way to locate the transition state.