Rep:Mod:EO1013TS
Introduction
GaussView 5.0.9 is a very powerful program that allows for complex quantum mechanical calculation to be performed on molecules. It was used to investigate several aspects of three Diels-Alder reactions, the orbital interactions (primary and secondary) were moedlled and closely inspected as well as the energies and transition states to better understand the reaction paths of the examples studied.
Potential Energy Surfaces (PES)
The concept of PES is fundamental in computational chemistry and has allowed for many breakthroughs. A PES displays the relationship between the energy of a molecule and its geometry.
The energies can be calculated using different computational methods that simplify and solve the Schrödinger equation (Eqn 1) using approximations allowing PES to be generated in very little time. A PES conatains a lot of information, namely global and local minima that represent stable confomers/rotamers of the same molecule with the transition state that links them.[1]
Nf710 (talk) 22:45, 10 January 2018 (UTC) Slight confusion here, in guassian (for the methods we are using) at each step in the optimsation we are only solving the time independent Schrodinger equation. We are only concerned with electronic distance from the nuclei wrt to energy.
The Transition State (TS) and Minima
In GaussView 5.0.9 there are various methods (discussed below) to allow for the calculation of energies after optimising a particular geometry to a minimum energy taking into account electron repulsion and several other factors. Methods have also been devised, making use of known atomic separations during transitions to hazard a guess at the TS before performing optimising calculations and running an Intrinsic Reaction Coordinate (IRC) calculation can be performed to plot a reaction profile diagram.
The value of gradient on the PES at the minimum and at the transition structure will both be zero. Minima will have a positive value for the second derivative in every axial direction of the energy potential surface whereas a TS will have a positive value for the second derivative (saddle point) in all axial directions apart from in the reaction coordinate. This means that at a minima, movement in any direction either side of that point will results in a geometry with a higher energy. The same is true for the TS but there is a decrease in energy in one dimension which is known as the reaction pathway. The PES has 3N-6 dimensions, where N is the number of atoms in the molecule of study, corresponding to the degrees of freedom available to the molecule. Running an IRC calculation on the Ts structure allows as to track the geometries along this pathway.[2]
The TS is a saddle point and just like a minima or a maxima, its first derivative will be zero. The difference however is apparent when you take the second derivative, which is done using a Hessian matrix in GaussView 5.0.9. The second derivative correlates to the energy and therefore the frequency and force constant of the vibrations in the molecule. As a result, minima always have positive force constants (increases in energy) and the TS, being a saddle point, will have at least one negative force constant (producing an imaginary vibration) which corresponds to the reaction pathway.
Nf710 (talk) 22:53, 10 January 2018 (UTC) Really good understanding of using the hessian. It is actually the eigen values of the matrix which give the force constants. And a TS will only 1 negative force constant as it is a first order saddle point and this is the reaction pathway.
Methods to Locate The TS
In this investigation, three main methods were used to find the transition state.
Method 1: This method only works if one has prior knowledge of the transition state. The transition state is guessed using empirically observed bond lengths and a minimisation calculation is performed. If these lengths are wrong, undesired structures could form.
Method 2: This method also requires prior knowledge of the transition state. A guess of the TS is made and the bonds involved in the reaction are frozen before a minimisation calculation is performed. This structure is then optimised to a TS and is more reliable that Method 1.
Method 3: This method does not require prior knowledge of the transition state as you start with the product or reactants (optimised to a minimum). Bonds are then added or removed to closer resemble the TS and similar to Method 2, these are frozen to obtain a minimum. However, It is not very reliable for TS geometries that do not resemble the minima.
Computational Methods
The PM6 and B3LYP methods were used in this lab. PM6 is a semi-empirical method which simplifies the Hartree-Fock method by using empirical data and pre-determined integrals to solve Hamiltonian (the energy operator of the Schrödinger equation) and as a result, runs very quickly as less calculations need to be performed. With all the approximations and generic data used in this method, results are often inaccurate.[3]
B3LYP, on the other hand, is a hybrid method that uses elements of Hartree-Fock and Density Funtional Theory (DFT). This method is more expensive than the PM6 as it doesn't use pre-determined integrals: it uses the DFT method to calculate all of the terms of the Hamiltonian apart from the exchange correlation term which is done using a HF method. It gives a very reliable results.[4][5]
Nf710 (talk) 22:55, 10 January 2018 (UTC) Good understanding. Essentially the DFT method calculates the energy as a function of electronic density rather than electronic postion. hence it is much faster. But you get the exchange correlation term which cannot be solved analytically.
Exercise 1: Butadiene + Ethene
(Fv611 (talk) Very good across the whole exercise. Well done!)
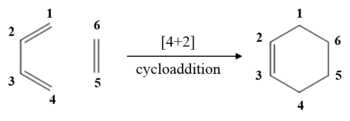
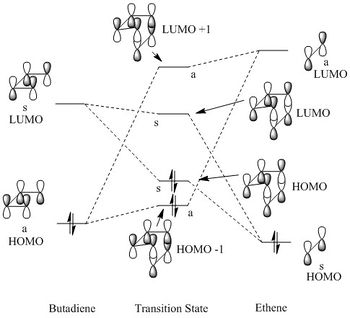
This reaction is a [4+2] cycloaddition. Butadiene and ethene react together to form cyclohexene. The diene is more electron-rich than the dienophile. As can be seen from Figure 2, the HOMO of butadiene contributes more to the HOMO-1 of the TS. In addition, the LUMO on ethene contributes more to the LUMO+1 which shows that HOMO of butadiene is lower in energy than the LUMO of ethene. This is an example of a normal electron demand reaction as the closest interaction is between the HOMO of the diene and the LUMO off the dienophile.[6]
Analysis of Molecular Orbitals
A non-zero overlap integral is required in order for an orbital interaction to be favourable. Orbitals involved in this interaction must have the same symmetry as the overlap integral is proportional to the spatial overlap of the orbitals in question. For a non zero overlap, the orbitals must both be symmetric or asymmetric to give overall symmetric function. An anti-symmetric function will be gained when you combine orbitals of different symmetry which will leads overlap integral being zero.[7]
|
|
|
|
|
| ||||||
|
|
Looking at the HOMO and the LUMO of the TS in Table 3, it is clear that they are formed from the HOMO of ethene and the LUMO of butadiene, both being symmetric orbitals. The opposite interaction from two antisymetic orbitals, the HOMO of butadiene and LUMO of ethene, give the HOMO-1 and the LUMO+1 of the TS. This clearly demonstrates that reactions can only be allowed when orbitals of the same symmetry can interact. Transition states that are of a geometry where orbitals of opposite symmetry are forced to interact will most likely lead to an unsuccessful reaction.
Analysis of Bond Lengths
| Bonds | Cyclohexene | Transition State | Butadiene and Ethene |
|---|---|---|---|
| C1-C2 | 1.501 | 1.380 | 1.335 |
| C2-C3 | 1.338 | 1.441 | 1.468 |
| C3-C4 | 1.501 | 1.380 | 1.335 |
| C4-C5 | 1.540 | 2.115 | ---- |
| C5-C6 | 1.541 | 1.382 | 1.327 |
| C6-C1 | 1.540 | 2.115 | ---- |
A typical carbon to carbon single bond length is 1.54 Å and a double bond is 1.34 Å.[8] These are a direct match with the bond lengths predicted by Gaussian. C1-C2 and C3-C4 are a lot shorter due to the pulling effect of the higher electron density in C2-C3. As the carbons change from and sp3 hybridised orbitals to sp2, the bond lengths shorten and vice versa. Both double bonds on butadiene also lengthen as they change from sp2 to sp3 hybridisation. The two new bonds (C4-C5 and C6-C1) that form in the TS have a bond length (2.115 Å) that is smaller than two times the Van der Waal radius of carbon (1.7 Å) showing that the two molecules are starting to interact during the transition state and get shorter once the bond forms into a single C-C bond.[9]
The Transition State
The vibration above (click toggle vibration) corresponds to the negative frequency in the TS calculations a result of the negative force constant. The bond formation is synchronous as the carbons at both ends of the new bonds are moving at the same time in the TS. This can also seen in the IRC (Figure 3) as the bonds are formed at the same time.
Relevant Files
Product (PM6-Optimised): File:PRODUCTS PM6 eo1016.LOG
TS of Reaction (PM6 Optimised): File:BOTH INITIAL IRC TS PM6 eo1013.LOG
IRC of Reaction: File:BOTH INITIAL IRC TS PM6 eo1013.LOG
Exercise 2: Reaction of Cyclohexadiene + 1,3-Dioxole

This Diels-Alder reaction ([4+2] cycloaddition) is particularly interesting as there is a possibility of having two products: the endo and exo products. This is due to the fact that the dienophile is substituted and can approach in two different orientations. The exo product is formed when the bulk of the substituent approaches in such a way that it it pointing away from the pi-system of the diene. When it approaches with the bulk of the dienophile facing towards the pi system of the diene, the endo product is formed. This has implications for the energies of the products as will be discussed in the following sections.

(Fv611 (talk) The MO diagram is nice, but you could have added a discussion of the difference between the exo and endo cases in terms of their TS MO energies.)
The oxygen in either side of the dienophile have an electron donating effect on the p-orbitals of the double bond, causing the dienophile to be "electron rich" and raising the energy of the HOMO and LUMO, compared to ethene, as a result. As a consequence, as can illustrated in Figure 5, the closest interaction is between the LUMO of the diene and the HOMO off the dienophile. Therefore, this is an example of an inverse electron demand reaction.[10]
Analysis of Molecular Orbitals
As mentioned before, the oxygens on the dioxole work to raise the energy of the HOMO and LUMO of the diene compared to ethene. This increases the energy gap and leads to weaker interactions. An example of this is the HOMO-1 which is still lower in energy than the HOMO of the reactants as it only experiences a slight destabilisation. Only orbitals of the same symmetry can interact as seen below in Table 5 and Table 6.
|
| ||||||
|
|
|
| ||||||
|
|
Thermochemical Analysis
| Product | Reaction Barrier in kJ mol-1 | Reaction Energy in kJ mol-1 |
|---|---|---|
| Endo | 158.47 | -68.75 |
| Exo | 166.30 | -65.15 |
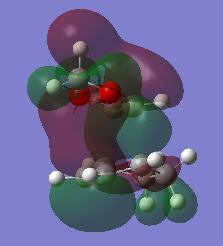
GaussView 5.0.9 also calculates the free energies of these geometries which can allow for an in-depth analysis of the energetics of the reaction. A summary of this data is presented in Table 7. The reaction barrier is calculated as the difference in energy between the TS and the starting materials. The endo product has a lower reaction barrier compared to the exo product, making it the kinetically-preferred product. This can be attributed to the extra stabilisation present in the endo transition state as a result of the secondary orbital interactions between the oxygens and the pi system on the diene. Figure 6 shows the orbital interaction between the oxygen (red atoms) with the double bond from.
The reaction energy is calculated as the free energy difference between the products and the reactants. Comparing the two shows that the endo reaction has a more negative reaction energy compared to the exo reaction, making the endo product the thermodynamically-preferred product. This can be rationalised, as seen in Figure 7, by the location of the CH2s on the-5 membered ring. There is some steric clash with the CH2 fragments in the exo product with he CH2s on the bridging carbons which isn't present in the endo product (making it more thermodynamically stable).
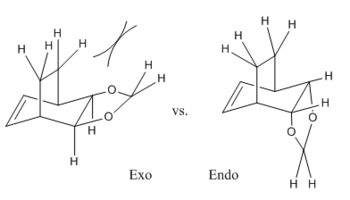
The endo product is both the kinetic and thermodynamic product. This also agrees with experimental observations stating that in a [4+2] cycloaddition, the endo product is preferred, even if the exo product is more stable, due to favourable secondary orbital interactions in the TS.
Relevant Files
1,3-Dioxole (B3LYP-Optimised): File:DIOXOLE B3LYP eo1013.LOG
Cyclohexadiene (B3LYP-Optimised): File:CYCLOHEXADIENE B3LYP eo1013.LOG
Endo Product (B3LYP-Optimised): File:ENDO PRODUCT PM6 eo1013.LOG
Exo Product (B3LYP-Optimised): File:EXO PRODUCT END B3LYP eo1013.LOG
IRC of Endo Reaction (PM6 Optimised): File:IRC PM6 ENDO eo1013.LOG
IRC of Exo Reaction (PM6 Optimised): File:IRC EXO PM6 eo1013.LOG
Nf710 (talk) 23:05, 10 January 2018 (UTC) Your energies are correct and you have come to the correct conclusions. You have nicely used diagrams to explain your points. If you wanted to quantitatively show the ordering of the orbitals. you could have run an energy calculation with both reactant on the same PES and then looked at the MOs.
Exercise 3: O-xylylene + SO2

This is another example of another interesting Diels-Alder reaction ([4+2] cycloaddition). As well as having the endo and exo products, this reaction can react to give the chelotropic product where a 5-membered ring is formed with two new bonds both formed to the sulphur. The other caveat to this reaction is that the reaction can occur on the double bonds within the ring to produce three more products: endo, exo and chelotropic. The analysis will be discussed below.
IRCs of the Exocyclic Reaction
The IRCs were run showing the geometries along the reaction coordinate. From Figure 9 and Figure 10 is can be seen that the exo and endo reaction proceed with asynchronous bonding, with the oxygen bonding before the sulphur. Figure 11 clearly shows that the chelotropic reaction bonding in a synchronous fashion.
Thermochemical Analysis
| Product | Reaction Barrier in kJ mol-1 | Reaction Energy in kJ mol-1 |
|---|---|---|
| Endo | 80.12 | -100.66 |
| Exo | 84.11 | -101.31 |
| Cheletropic | 102.44 | -157.65 |
GaussView 5.0.9 was used to calculate the energetics of the three reactions at the PM6 level. From Table 8 it can be seen that the chelotropic product has the lowest reaction energy and is therefore the thermodynamic product. A consideration of the bond enthalpies involved makes this quite clear, the formation of C-O and S-O is less favorable compared to the formation of S=O and S-C.[11] It also has the highest energy TS largely due to the the 5-membered ring in the TS which suffers from ring strain compared to 6-membered TS in the endo and exo reaction pathways. Because of this higher energy transition state, the other products will be expected to form in a greater proportion under equilibrium conditions.
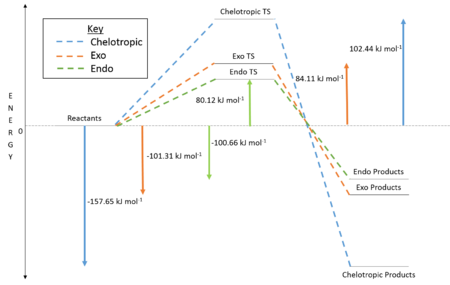
Figure 12 illustrates that the endo product has the lowest energy TS and is therefore the kinetic product. These reactions are all very favourable due to the fact that an aromatic ring in formed afterwards. The stabilisation due to aromatisiation is very desired as we can see that ir is large enough to compensate for the high TS energy of the chelotropic reaction. Looking at the IRCs we can see that the aromatic ring forms before the other bonds in the reaction.
Relevant Files
Sulphur Dioxide (PM6 Optimised): File:SO2 PM6 EO1013.LOG
O-xylylene (PM6 Optimised): File:XYLYLENE NEW PM6 EO1013.LOG
Chelotropic TS (PM6 Optimised): File:TS OPTIMISED FINAL PM6 che eo1013.LOG
Exo TS (PM6 Optimised): File:TS PM6 FINAL EXO eo1013.LOG
Endo TS (PM6 Optimised): File:TS PM6 ENDO FINAL eo1013.LOG
Chelotropic Product (PM6 Optimised): File:PRODUCTS PM6 che eo1013.LOG
Exo Product (PM6 Optimised): File:EXO PRODUCT PM6 FINAL eo1013.LOG
Endo Product (PM6 Optimised): File:PRODUCTS PM6 ENDO FINAL eo1013.LOG
Alternative Reaction Pathway
| Product | Reaction Barrier in kJ mol-1 | Reaction Energy in kJ mol-1 |
|---|---|---|
| Endo | 110.34 | 14.62 |
| Exo | 118.18 | 19.06 |
From Table 9, it is clear that the products are less stable than the sum of the energies of the reactants at infinite separation, this is a strong indication that the reaction requires some energy input in order for it to occur (endothermic reaction). The reaction barriers are a lot higher in comparison to those in Table 8 which makes sense as there is the lack of stablisation gained from forming an aromatic ring from this pathway. The IRCs (Figure 13 and Figure 14) are shown below.
Relevant Files (Alternative Pathway)
Alternative Exo TS (PM6 Optimised): File:TS EXO FINAL PM6 ALT eo1013.LOG
Alternative Endo TS (PM6 Optimised): File:TS ENDO FINAL PM6 ALT eo1013.LOG
Alternative Exo Product (PM6 Optimised): File:PRODUCT EXO PM6 ALT eo013.LOG
Alternative Endo Product (PM6 Optimised): File:PRODUCT ENDO PM6 ALT eo1013.LOG
Conclusion
In conclusion, the results from this lab agree with the established theory around Diels-Alder reactions. Using the PM6 allows for quick calculations that may not be so reliable but aid an understanding of the underlying chemistry. The B3LYP calculations are very reliable but are more expensive in terms of computational cost. GaussView 5.0.9 has proven to be a very useful tool in analysing the thermochemical data of reactions and visualising the MOs to understand favourable orientations for successful reactions.
Exercise 1 was useful in understanding the advantages and limitations of the computational methods chosen. Analyzing and comparing the C-C bond lengths reflected how close GaussView 5.0.9 can get to literature values. Exercise 2 required more in-depth analysis of the energies of the optimised geometries and shows how effective computational chemistry can be in predicting the major product of a reaction. Exercise 3 highlighted the importance of utilising our chemical intuition along with the computational methods to investigate alternative pathways to rationalise their feasibility which could prove useful in determining possible side reactions.
All in all, these exercises have shown that the computational approach is a very powerful one indeed and can be used to predict the course, outcomes and shortcomings of a reaction before even entering the lab. This has some very beneficial implications namely in the fact that money can be saved rather than being spent on reagents for a reaction that will not yield desired products. It also proves to be a very useful tool in understanding reaction dynamics/mechanisms.
References
- ↑ The Concept of PES, http://is.muni.cz/el/1431/podzim2015/C9920/um/The_concept_of_PES.pdf, (accessed December 2017)
- ↑ Gaussian – Vibration Analysis in Gaussian, http://gaussian.com/vib, (accessed December 2017)
- ↑ Gaussian – Semi-Empirical Methods, http://gaussian.com/semiempirical, (accessed December 2017)
- ↑ What is B33LYP?, http://www.quora.com/What-is-B3LYP-and-why-is-it-the-most-popular-functional-in-DFT, (accessed December 2017)
- ↑ A. Szabo and N. S. Ostlund, Modern Quantum Chemistry, Dover Publications, 1989.
- ↑ J. Clayden, N. Greeves and S. Warren, Organic Chemistry, Oxford University Press, 2nd edn., 2012.
- ↑ P. W. Atkins and J. De. Paula, Atkins' Physical Chemistry, Oxford University Press, 9th edn., 2006.
- ↑ L. Pauling and L. O. Brockway, ELECTRON DIFFRACTION INVESTIGATION OF SOME HYDROCARBONS, California Institute of Technology, 1937.
- ↑ A. Bondi, van der Waals Volumes and Radii , J. Phys. Chem., vol. 68 #3, 1964.
- ↑ J. Clayden, N. Greeves and S. Warren, Organic Chemistry, Oxford University Press, 2nd edn., 2012.
- ↑ PROPERTIES OF ATOMS, RADICALS, AND BONDS, http://labs.chem.ucsb.edu/zakarian/armen/11---bonddissociationenergy.pdf, (accessed December 2017)
