Jump to content

Rep:Mod:EMorcomC1

From ChemWiki

Day 1 10/11/14

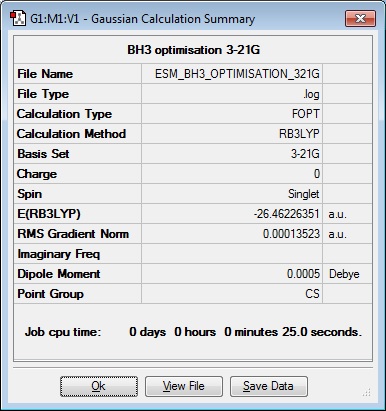
An optimisation calculation on BH3 was carried out by displacing one of the B-H bond lengths to 1.54 Angstroms and keeping the other two at 1.53 Angstroms. The method used was B3LYP and the basis set was 3-21G.

Optimised BH3 Molecule
Bond Length Bond angle with next H going clockwise
1.19 120.0
1.19 120.0
1.19 120.0

Optimisation log file here


Optimised BH3 Molecule
Summary Data Convergence Jmol
Item Value Threshold Converged? 
Maximum Force            0.000296     0.000450     YES
RMS     Force            0.000161     0.000300     YES
Maximum Displacement     0.001068     0.001800     YES
RMS     Displacement     0.000616     0.001200     YES
Predicted change in Energy=-3.549028D-07
Optimization completed.
   -- Stationary point found.
BH3


Open Jmol file in Notepad

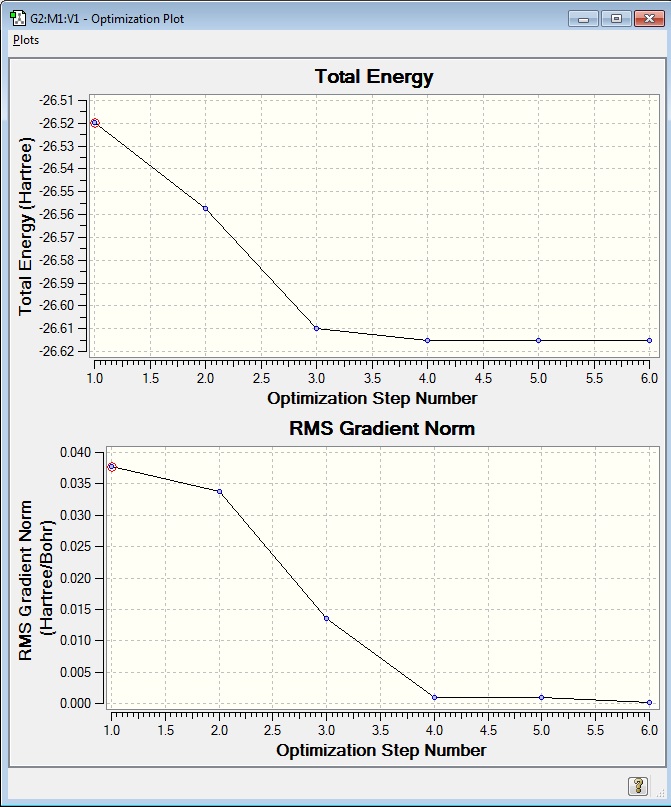
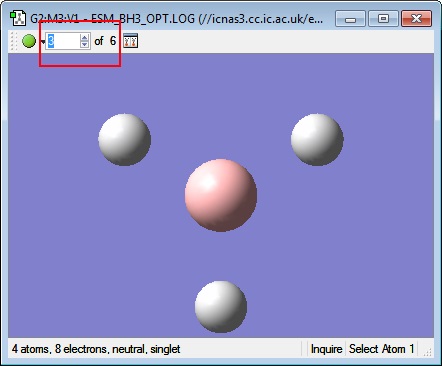
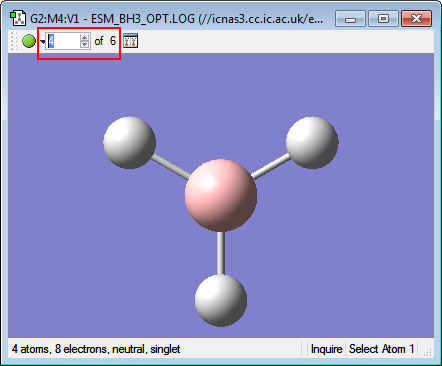
Examining the structures along the plot at different Optimisation Steps, it is possible to see that GaussView's threshold bond distance has been reached after optimisation step 3. (See images below) Another possible choice for the defining the existence of a bond would be the Van der Waal's distance between the two atoms- if the distance between the atoms were shorter than the sum of each atom's Van der Waal's radius, a bond could be drawn.

Day 2 11/11/14

BH3

Optimised BH3 Molecule 6-31G(d,p)
Results Table Converged? Jmol
Item Value Threshold Converged? 
Maximum Force            0.000285     0.000450     YES
RMS     Force            0.000155     0.000300     YES
Maximum Displacement     0.001035     0.001800     YES
RMS     Displacement     0.000596     0.001200     YES
Predicted change in Energy=-3.308800D-07
Optimization completed.
   -- Stationary point found. |
BH 6-31G(d,p)

Optimisation file here

BH3
B-Ha Bond length Ha-B-H (going clockwise) angle / o
1.19292 119.996
1.19247 119.996
1.19292 120.009

The energy of this molecule cannot be compared to the energy calculated for the previous molecule because the basis sets used were different. Exactly the same computational method and number of atoms computed with the same basis set for each and every atom have to be used before two molecule energy calculations are comparable. Energies need to be reported in au up to 7 decimal places and with same methods and basis sets!

GaBr3

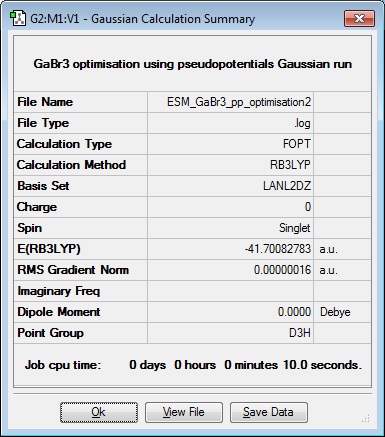
For the GaBr3 molecule the HPC computer said the submission was pending after waiting the whole morning, so the calculation was done on the Local computer and results below are given from this data. Optimisation file here

GaBr3
Results Summary Converged? Jmol
Item Value Threshold Converged? 
Maximum Force            0.000000     0.000450     YES
RMS     Force            0.000000     0.000300     YES
Maximum Displacement     0.000003     0.001800     YES
RMS     Displacement     0.000002     0.001200     YES
Predicted change in Energy=-1.282692D-12
Optimization completed.
   -- Stationary point found. |
GaBr3

Optimisation file here

GaBr3
Ga-Br Bond length (Å) Br-Ga-Br angle ( o )
2.35 120.0

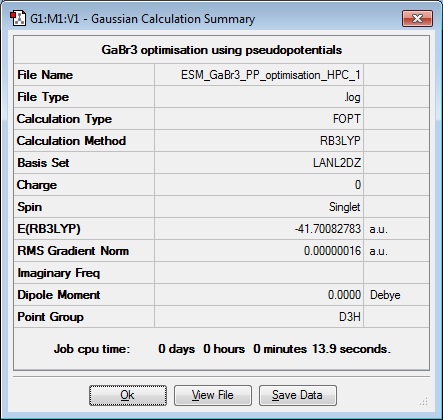
The following data was obtained from the HPC after the submission was returned, the original set of data, run by Gaussian has been left as a record of what happened during the lab, and for possible comparison of the results.

As can be seen from the results table, the energies calculated by the local computer and the HPC are very similar. However, if the molecule were much bigger, the local computer would not have the capacity to do the calculation in a reasonable time.

GaBr3 Run by HPC
Results Summary Converged? Jmol
Item Value Threshold Converged? 
Maximum Force            0.000000     0.000450     YES
RMS     Force            0.000000     0.000300     YES
Maximum Displacement     0.000003     0.001800     YES
RMS     Displacement     0.000002     0.001200     YES
Predicted change in Energy=-1.282693D-12
Optimization completed.
   -- Stationary point found. |
GaBr3

DOI:10042/85065


GaBr3 HPC
Ga-Br Bond length (Å) Br-Ga-Br angle ( o )
2.35 120.0

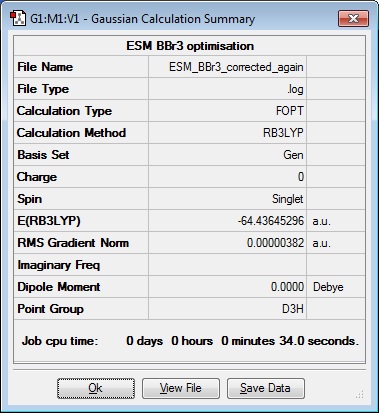
BBr3

A BBr3 calculation was submitted to the HPC at 15:17, but the Status remained as 'Pending' for the rest of this lab session, so this was completed once the submission was returned. The following day (12/11/14) the submission was returned and the analysis could be continued.


BBr3 Run by HPC
Results Summary Converged? Jmol
Item Value Threshold Converged? 
Maximum Force            0.000008     0.000450     YES
RMS     Force            0.000005     0.000300     YES
Maximum Displacement     0.000036     0.001800     YES
RMS     Displacement     0.000023     0.001200     YES
Predicted change in Energy=-4.027258D-10
Optimization completed.
   -- Stationary point found. |
BBr3

DOI:10042/87662

BBr3
B-Br Bond length (Å) Br-B-Br angle ( o )
1.93 120.0

Comparison of the Data

Geometry Data
BH3 GaBr3 BBr3
r(E-X) (Å) 1.19 2.35 1.93
θ(X-E-X)degrees (º) 120.05 120.0 120.0

Answers to questions

What difference does changing the ligand have? How are H and Br similar and different?

Changing the ligand changes the length of the bond but does not affect the angle between the bonds. Hydrogen is a much smaller atom than Bromine, which has a 34 more electrons than Hydrogen. Because of this, Br forms bonds at a greater distance than those with H. Bromine and hydrogen are both one electron short of a filled orbital; 1s for Hydrogen and 4p for Bromine. So they can both form covalent bonds with electron rich central atoms.

What is the difference of changing the central atom? How are B and Ga similar and different?

Changing the central atom also changes the bond length; a larger central atom forms longer bonds. Ga and B are both in Group 13, so they have similar properties- both have a single electron in their outermost p orbital, but Ga is bigger than B as its valence orbital is 4p1.

What is a bond? A very simplified definition of a chemical bond is a link between atoms.[1] This can be either due to the Coulombic attractions between ions, or the attraction of two nuclei to the shared electrons between them, or anywhere on a sliding scale between these two. A more realistic description can be gained by using Molecular Orbital theory whereby the atomic orbitals containing electrons are combined to create new, molecular orbitals, where the electron density is spread over the molecule. This can help the definition of different types of bond according to the combination of orbitals because the orbitals have to be of the appropriate energy and symmetry to interact to form both a bonding and an antibonding orbital, and certain interactions are stronger than others.[1] This gives rise to sigma bonds where the contributing orbitals all have cylindrical symmetry around the internuclear axis.[1] These bonds are generally strong because the overlap of the orbitals is direct, in comparison to π molecular orbitals where the interaction of two p orbitals is ‘sideways on’. The strength of the interaction depends on the overlap integral between the atomic orbitals that make up the molecular orbitals, so orbitals that are further apart will overlap less.[1]

The problem with assigning chemical bonds as either strong, medium or weak is that there is not really one definitive scale because it depends on the context of the chemistry in question. In the context of organic chemistry, a Si-O bond is strong (466 kJ mol-1), while a C-C bond could be considered as ‘medium strength’ (348 kJ mol-1).[1] An example of a weak chemical bond is a hydrogen bond, that is the result of the interaction of an electronegative atom in a molecule attracting a hydrogen bonded to an electronegative atom in another molecule. A hydrogen bond is two orders of magnitude smaller than the chemical bond energies of H-O, H-N, H-F and H-Cl.[2] However, hydrogen bonds are stronger than dispersion forces, so when looking at the physical properties of a mole of atoms, and how they interact with each other, hydrogen bonds are going to have significant effects.


In some structures gaussview does not draw in the bonds where we expect, why does this NOT mean there is no bond?

Gaussview has been programmed to indicate a chemical bond exists once the distance between two atoms is at or smaller than a predetermined threshold.[3] However, this does not help the precise determination of whether or not a bond is there because, as previously discussed, a bond is a link between atoms, and this can be quantified by calculating the energy of the interaction and deciding critically whether such an interaction is actually a bond or not, regardless of Gaussview's interpretation of the data, which is just following instructions without analysis.

Day 3 12/11/14

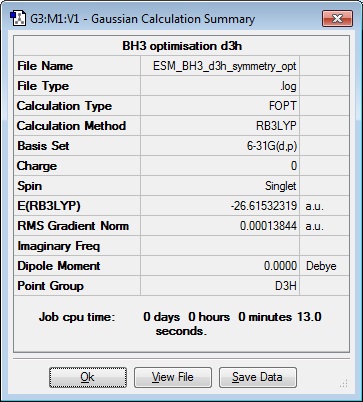
Symmetry

Opened 6-31G(d,p) file from previous day, and checked for D3h symmetry, but the results table showed Cs point group, so 'enable point group symmetry' was ticked, 'symmetrize' was selected and the molecule was constrained to D3h symmetry.

BH3
Results Summary Converged? Jmol
Item Value Threshold Converged? 
Maximum Force            0.000277     0.000450     YES
RMS     Force            0.000181     0.000300     YES
Maximum Displacement     0.001099     0.001800     YES
RMS     Displacement     0.000720     0.001200     YES
Predicted change in Energy=-4.564844D-07
Optimization completed.
   -- Stationary point found. |
BH3


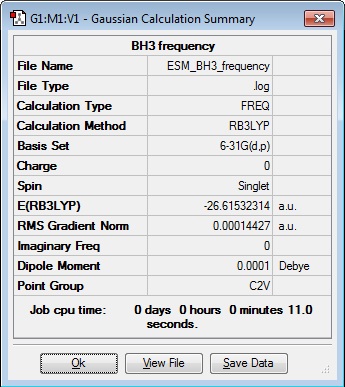
A Frequency calculation was carried out for the D3h optimised BH3 molecule.

BH3
Results Summary Converged? Jmol
Item Value Threshold Converged? 
Maximum Force            0.000276     0.000450     YES
RMS     Force            0.000144     0.000300     YES
Maximum Displacement     0.001132     0.001800     YES
RMS     Displacement     0.000568     0.001200     YES
Predicted change in Energy=-4.915339D-07
Optimization completed.
   -- Stationary point found. |
BH3

When the file was opened to analyse the low frequencies, the "zero" frequency had three values of the order of 50 cm-1. So progress was halted until a demonstrator was available to consult.

13/11/14

Vibrational Frequencies

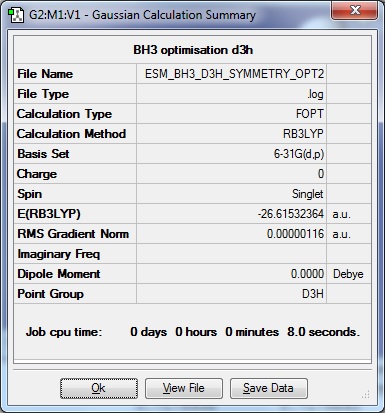
To re-optimise the molecule as the Thresholds in the Item table were too high: a code was typed into Additional Keywords (scf=conver=9) and the "Use tight convergence criteria" box was checked to try an obtain the desired limit of maximum variation of ±15 cm-1 in the Low frequencies.

The re-optimised BH3 molecule data is shown below:

BH3
Results Summary Converged? Jmol
Item Value Threshold Converged? 
Maximum Force            0.000002     0.000015     YES
RMS     Force            0.000002     0.000010     YES
Maximum Displacement     0.000009     0.000060     YES
RMS     Displacement     0.000006     0.000040     YES
Predicted change in Energy=-3.183927D-11
Optimization completed.
   -- Stationary point found. |
BH3

Optimisation file here

The resultant optimised BH3 molecule then underwent a frequency calculation.

BH3
Results Summary low modes
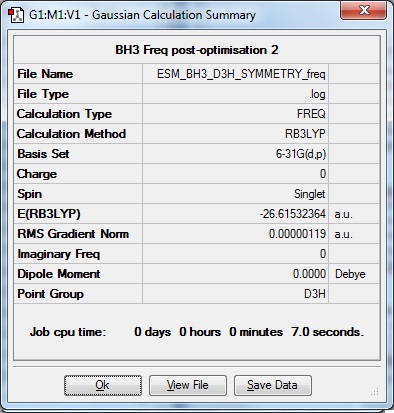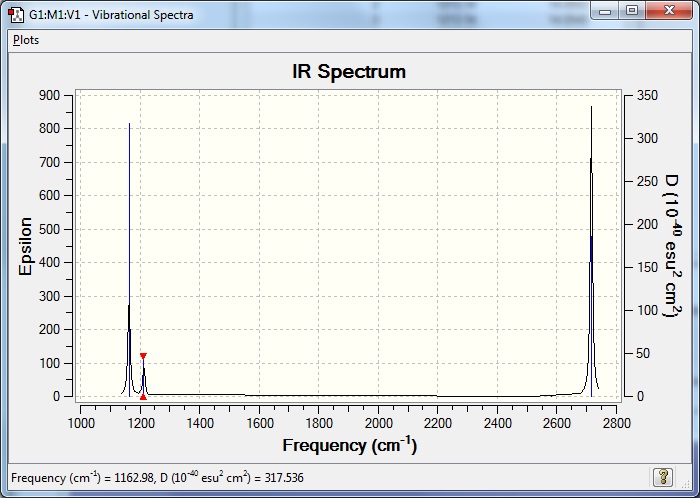
Low frequencies --- -10.7276 -10.7174 -4.6132 0.0005 0.0399 0.4675 
Low frequencies --- 1162.9815 1213.1436 1213.1439

Frequency file here

Vibrational Spectrum for BH3
Wavenumber (cm-1) Intensity IR Active? Type
1163 93 yes bend
1213 14 very slight bend
1213 14 very slight bend
2583 0 no stretch
2716 126 yes stretch
2716 126 yes stretch


Fewer than six peaks are observed in the IR spectrum because not all of them are IR active. In order for a molecule vibration to be IR active, there needs to be a change in dipole moment of the molecule once the vibration occurs. The stretch at 2583 cm-1 corresponds to the totally symmetric stretch of all three B-H bonds stretching synchronously in one plane, this leads to no change in dipole as they are always equidistant from B and all 120° from each other.

GaBr3 Frequencies

GaBr3
Results Summary low modes
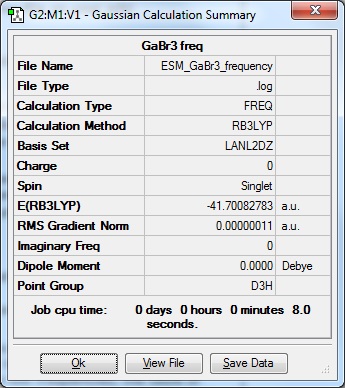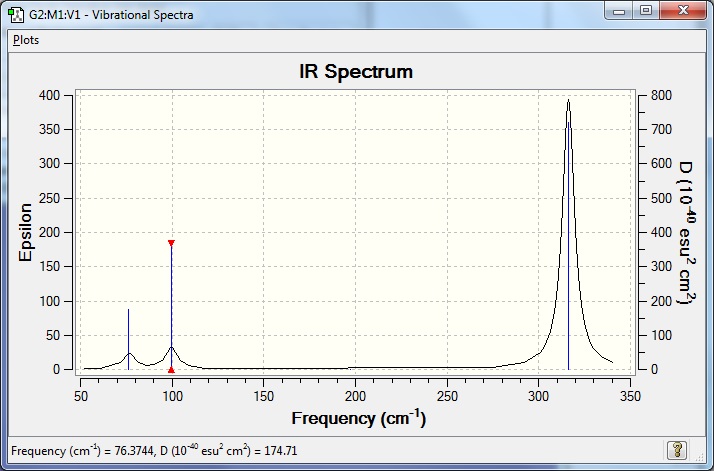
Low frequencies --- -0.5252 -0.5247 -0.0024 -0.0010 0.0235 1.2010 
Low frequencies ---   76.3744   76.3753   99.6982
Vibrational Spectrum for GaBr3
Wavenumber (cm-1) Intensity IR Active? Type
76 3 extremely slight bend
76 3 extremely slight bend
100 9 extremely slight bend
197 0 no stretch
316 57 yes stretch
316 57 yes stretch


Frequency file here

DOI:10042/90657

Answers to questions

What does the large difference in the value of the frequencies for BH3 compared to GaBr3 indicate?

The stretching and bonding force constants of molecule can be taken to be independent of each other as a good first approximation.[4] Calculation of the vibrational energies of polyatomic molecule have been found to be well-approximated by calculating the individual vibrational energy of each bond in the polyatomic and treating that fragment as a diatomic molecule.[5] The vibrational energy of a diatomic, modelled as a harmonic oscillator, depends on the force constant, kf and the molecule’s effective mass where the force constant f = (d2V/dx2)0 and the effective mass, meff = (m1m2)/(m1+m2).[1] The energy of the vibrational states is proportional to (kf/meff1/2.[1] Thus it is easy to see that if the masses of the two atoms are large, the effective mass will be greater than that for smaller atoms, and the vibrational energies will be lower. The vibrational frequencies of BH3 are therefore much greater than those of GaBr3 as Ga and Br are heavier atoms than B and H.


As can be seen from the animations, there is some motion in the Ga-Br bond in the central plane of the umbrella motion that is not present in the BH3 vibrations.

The A2'' umbrella motion for BH3 has a frequency of 1163 cm-1 and an IR intensity of 92.6, while GaBr3's A2'' frequency is 100 cm-1 and the IR intensity is 9.2. Both the BH3 and GaBr3 displacement is in the z-axis, but the distance between the central atom and its substituents is much greater for GaBr3. It can also be seen that the vibration for BH3 is much stronger than for that of GaBr3.

Why must you use the same method and basis set for both the optimisation and frequency analysis calculations?

The same method and basis sets need to be used for both the potimisation and the frequency analyses so that the results are comparable for having been done in the same way, to the same degree of accuracy.

What is the purpose of carrying out a frequency analysis?

A frequency analysis shows that a minimum has been reached because the low modes are sufficiently small. If they are large, or highly negative, then it is an indicator that the optimisation did not work.

What do the "Low frequencies" represent?

For all non-linear molecules, there are 3N-6 vibrational frequencies. The low modes are the six 'other' frequencies, these are the translational and rotational motions of the molecule. One dimension for each translation and one for each rotation, making six. (This is the reason that linear molecules' vibrational frequencies are given by 3n-5, because they only have two rotations that change the molecule.)[1]

Molecular Orbitals of BH3

DOI:10042/90668

From the comparison of the MO diagram generated and the orbitals calculated by the computer, it is clear that the qualitative MO theory, using just the combination of atomic orbitals to visualise the molecular orbitals, is comparable to the computational quantitative method. However, it only allows us to imagine what the ultimate orbital could look like, and does not provide a quantitative measure of the distribution. Conversely, having a basic knowledge of how MO theory works means that going the other way; looking at a computer-generated MO and trying to rationalise where those interactions came from, a lot easier.

NH3

Ran optimisation of NH3 using 6-31G(d,p) basis set.

NH3
Results Summary Converged? Jmol
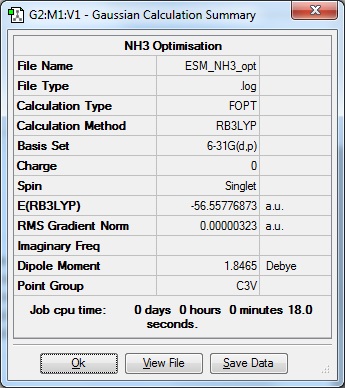Item Value Threshold Converged? 
Maximum Force            0.000006     0.000015     YES
RMS     Force            0.000004     0.000010     YES
Maximum Displacement     0.000012     0.000060     YES
RMS     Displacement     0.000008     0.000040     YES
Predicted change in Energy=-9.843769D-11
Optimization completed.
   -- Stationary point found. |
NH3

Redid optimisation with additional keywords scf=conver=9

NH3
Results Summary Converged? Jmol
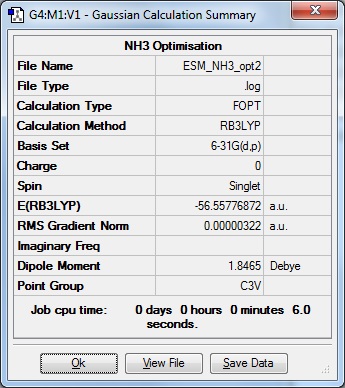Item Value Threshold Converged? 
Maximum Force            0.000006     0.000015     YES
RMS     Force            0.000004     0.000010     YES
Maximum Displacement     0.000016     0.000060     YES
RMS     Displacement     0.000011     0.000040     YES
Predicted change in Energy=-1.228052D-10
Optimization completed.
   -- Stationary point found. |
NH3

Optimisation file here

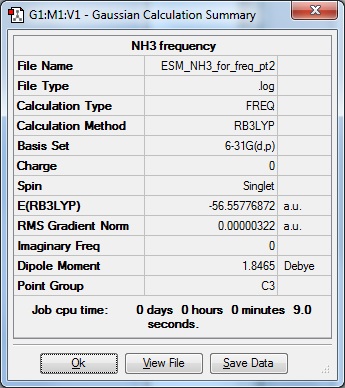
Ran frequency calculation on Gaussian

The low frequencies were low and within 15 cm-1 of each other, so proceeded to next part.

Frequency Calculation

NH3
Results Summary Low modes
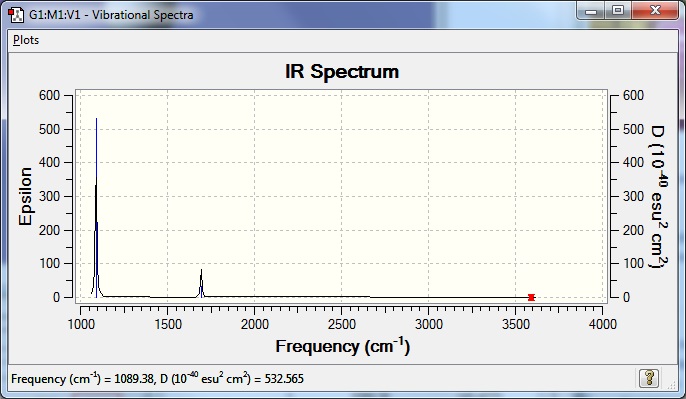
Low frequencies --- -0.0138 -0.0030 0.0013 7.0781 8.0927 8.0932

Ask about low frequencies being negative! 

Low frequencies --- 1089.3840 1693.9368 1693.9368

Frequency file here

Vibrational Spectrum for NH3
Wavenumber (cm-1) Intensity IR Active? Type
1089 145 yes bend
1694 14 very slight bend
1694 14 very slight bend
3461 1 extremely slight* stretch
3590 0** no stretch
3590 0** no stretch

*This is not visible on the actual spectrum but the heading is 'IR Active?', not 'IR visible?' so they have been counted even though they are so small as to be negligible on a spectrum. *Although the calculation gave 0.27, the accuracy of the method and basis set used means is not sufficient to say that these computed stretches are there.

Opened NH3 .chk file, and set Method to Energy, used Additional Keywords pop=full, and Full NBO settings, submitted calculation to HPC.

MO analysis file here

Natural Bond Order Analysis

Charge distribution of NH3 Charge Limits -1.000 to +1.000
NBO Charges
Atom Charge
Nitrogen -1.125
Hydrogen 0.375

The charge distribution is as expected for the ammonia as the Nitrogen is significantly more electronegative than the hydrogen and thus has negative charge localised on the nitrogen and positive charge on each of the hydrogens.

This optimised molecule can now be used for the following computation.

NBO file here

Day 5 14/11/14

Association energies: Ammonia-Borane

What is the energy of the dative bond of ammonia-borane?

Method: Ground State, Default Spin, B3LYP. Basis set: 6-31G(d,p). Additional keywords: integral=grid=ultrafine scf=conver=9. Use Tight convergence criteria ticked.


Ammonia-borane
Results Summary Converged? Jmol
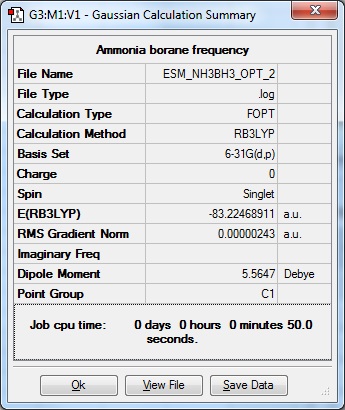Item Value Threshold Converged? 
Maximum Force            0.000003     0.000015     YES
RMS     Force            0.000002     0.000010     YES
Maximum Displacement     0.000051     0.000060     YES
RMS     Displacement     0.000018     0.000040     YES
Predicted change in Energy=-3.050916D-10
Optimization completed.
   -- Stationary point found. |
NH3BH3

File:ESM NH3BH3 opt2.mol

Optimisation file here

Ammonia-borane
Results Summary Low modes
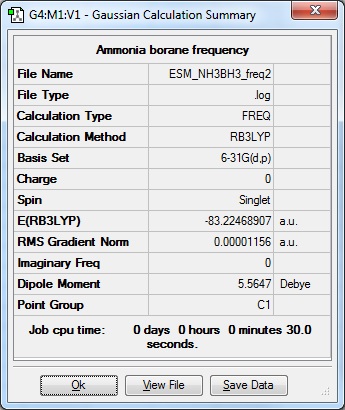Low frequencies --- -0.9358 -0.0005 0.0005 0.0007 4.0468 7.9192 
Low frequencies ---  263.7105  632.9836  638.5595

Frequency file here

Energy
Molecule Energy (a.u.)
BH3 -26.61532364
NH3 -56.55776872
NH2BH2 -83.22468907 
ΔE = E(NH3BH3)-[E(NH3)+E(BH3)]
   = -0.051596639 a.u.
   = -135.47 kJ mol-1

This is a sensible value for the bond energy between the lewis acidic BH3 and the basic NH3, because it is not so weak that the molecule would not form, but equally it is not so strong that it could not be considered as a hydrogen source. In the scale of strong to weak bond, this would be classed as on the weaker side of a medium strength bond. Bearing in mind that earlier, a C-C bond was given as a marker for a medium strength bond, and that is 348 kJ mol-1.[1]

Optional work on ethane

Ethane run on HPC with Method: Ground set, Default Spin, B3LYP. Basis set: 6-31G(d,p).'Use tight convergence criteria' ticked. Additional Keywords: integral=grid=ultrafine scf-conve=9

Ethane
Results Summary Converged? Jmol
Item Value Threshold Converged? 
Maximum Force            0.000003     0.000015     YES
RMS     Force            0.000001     0.000010     YES
Maximum Displacement     0.000015     0.000060     YES
RMS     Displacement     0.000006     0.000040     YES
Predicted change in Energy=-9.162129D-11
Optimization completed.
   -- Stationary point found. |
Ethane

Optimisation: DOI:10042/93507

After this, there was not sufficient time to complete analysis on ethane.

Week 2

Week 2 was a mini project, investigating some different molecules using the techniques accrued in week 1. The chosen project was Ionic Liquids. Ionic liquids are liquids consisting entirely of ions, usually with melting points below 100 °C, thus exhibiting ionic conductivity. They are often formed from organic salts or a mixture of organic and inorganic salts.[6]

Properties of ionic liquids that make them of particular interest to chemists include their wide range of solubilities and miscibilities, wide liquid ranges in comparison with molecular solvents, and their negligible vapour pressures, meaning they do not evaporate under normal condition. These properties help to make them particularly useful as solvents, and as the properties of the liquid can be changed by changing the constituent ions, they are also known as 'designer solvents'.[6]

Comparison of selected 'onium' cations

[N(CH3)4]+

Optimisation 1

Optimisation was carried out on the following cations using tight convergence criteria, with Additional Keywords: integral=grid=ultrafine scf=cover=9, basis set 6-31G(d,p), Ground state, default spin, B3LYP.

Optimisation Table
Results Summary Converged? Jmol
Item Value Threshold Converged? 
Maximum Force            0.000014     0.000015     YES
RMS     Force            0.000003     0.000010     YES
Maximum Displacement     0.000014     0.000060     YES
RMS     Displacement     0.000004     0.000040     YES
Predicted change in Energy=-2.297619D-10
Optimization completed.
   -- Stationary point found. |
[N(CH3)4]+
heading heading
Bonds Lengths (Å)
N-C 1.51
C-H 1.10
[N(CH3)4]+
heading heading
Bonds Angles (°)
C-N-C 109.5
N-C-H 108.9
H-C-H 110.0

Optimisation file: DOI:10042/101471

Because the subsequent molecules could not be computed with 'tight convergence criteria' ticked or the additional keywords 'scf=conver=9', a calculation was carried out on [N(CH3)4]+ using exactly the same method as the following molecules to allow for a comparison in the analysis. The results of this optimisation are shown below:

Optimisation Table
Results Summary Converged? Jmol
Item Value Threshold Converged? 
Maximum Force            0.000069     0.000450     YES
RMS     Force            0.000017     0.000300     YES
Maximum Displacement     0.000896     0.001800     YES
RMS     Displacement     0.000259     0.001200     YES
Predicted change in Energy=-5.165532D-08
Optimization completed.
   -- Stationary point found. |
[N(CH3)4]+
heading heading
Bonds Lengths (Å)
N-C 1.51
C-H 1.09
[N(CH3)4]+
heading heading
Bonds Angles (°)
C-N-C 109.5
N-C-H 108.9
H-C-H 110.0

Optimisation file: DOI:10042/109231

Frequency Analysis 1
Optimisation Table
Results Summary Low modes
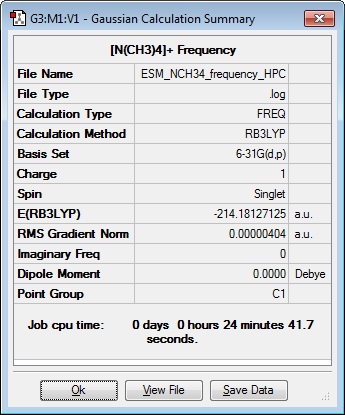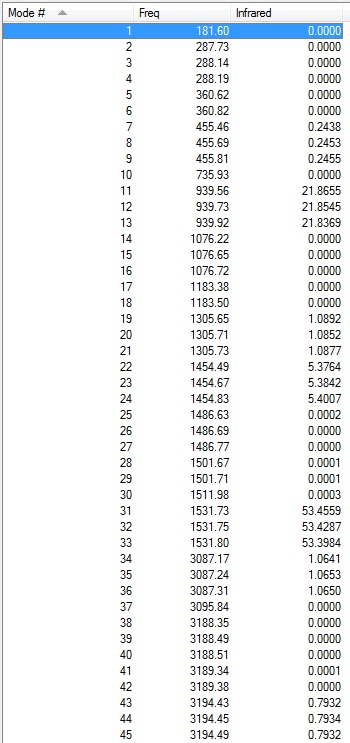
Low frequencies --- -16.8267 -0.0007 0.0004 0.0005 1.3954 2.8585 
Low frequencies ---  181.5990  287.7282  288.1388

It was noted that one of the formally zero frequencies is outside the range of ± 15 cm-1. This is due to the basis set not being quite good enough, and there are some very soft vibrational modes.

Frequency file: DOI:10042/101536

As can be seen from a comparison of the Table showing the vibrational modes and the IR spectrum as visualised by Gaussian, there is a large number of vibrations which are not IR active. This is expected due to the highly symmetric nature of the molecule so many vibrations will not involve a change in dipole moment.


Frequency file from optimisation done without the 'tight convergence criteria' ticked, or additional keywords 'scf=conver=9':

DOI:10042/109330

Optimisation Table
Results Summary Low modes
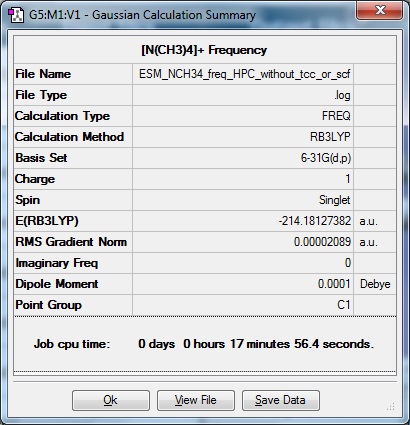Low frequencies --- -0.0014 -0.0011 0.0002 7.4670 7.8567 9.8999 
Low frequencies ---  184.0096  289.6040  289.6833
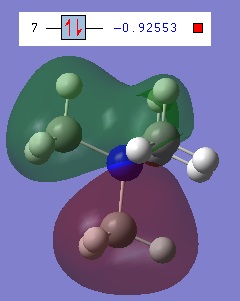
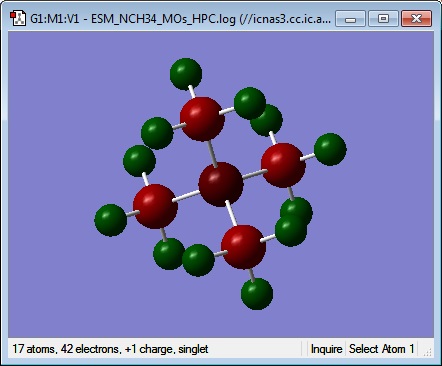
Molecular Orbitals 1

MO file: DOI:10042/101622

The MOs shown are those obtained from the second calculation so that the Homo and LUMO are suitable for comparison with the subsequent molecules.

6 is a totally bonding MO containing no nodes. It would be made of all the s-orbital contributions from the carbons and the nitrogen, possibly with a very small contribution form the hydrogens, but this could just be to the calculation not generating fully accurate MOs. It is delocalised over the whole molecule showing very strongly bonding interactions.

7 is the second lowest non-core orbital and it has one nodal plane at the nitrogen, corresponding to a p-orbital of the nitrogen interacting with the C-H3 fragments with sufficient symmetry and orientation. Because the node is centred on the nitrogen and is simply the symmetry associated with a p orbital, this is still a highly bonding orbital. Further confirmation of this being a nitrogen p-orbital interactions is found when it is noted that orbitals 7, 8 and 9 are degenerate and have similar shapes, all perpendicular to each other.

12 has two clear nodal planes on the N and C, with a small degree of curvature, and showing some significant through-space interactions between the hydrogens on adjacent methyl groups around one C3 axis going through a C-N bond. The atomic orbital interactions contributing to this orbital are not as strong as those before, but they are still quite strongly bonding. Again, this orbital is showing degeneracy with two other orbitals, but the orientation and shape of the orbitals is not so similar as before with 7, 8 and 9; indicating that there are more complicated orbital interactions than in the above orbitals.

15 has two formal nodal planes which cross both at and between the carbon atoms and all at the nitrogen, which does not have any AOs involved in this orbital. This indicates that this orbital is formed from carbon sp3 orbitals interacting with hydrogen s orbitals, and the through space interactions of these orbitals across the methyl groups. This is backed up by checking the NBO analysis file and seeing that all the carbon-hydrogen bonds are formed from hydrogen 1s AOs and carbon sp3 hybridised orbitals. It has a few weakly out-of-phase through-space interactions between the hydrogens, however, overall it is a bonding molecular orbital because of the strength of the in-phase through-bond interactions.

18 shows the most antibonding character of all the occupied orbitals that aren’t the three degenerate HOMOs. However, as this molecule is stable, and the orbital is occupied, it is still highly bonding. In relative terms to the other, more highly bonding orbitals, this orbital is relatively antibonding because there are several through-space antibonding interactions between the hydrogens. The carbon p orbitals are interacting in-phase with the hydrogen s orbitals, except on one methyl group, where it appears that the calculation was not quite optimised and it is possible to imagine this methyl following the same pattern of of the orbitals on the other methyl substituents.

If these are the methyl groups viewed down the C-N bond, one can visualise the interaction of these degenerate fragment orbitals with the carbon sp3 hybridised orbitals, leading to the formation of the orbitals seen in the Gaussian-generated MO above.
NBO Analysis 1
Charge Distribution - Colour range -1.000 to +1.000


Formal Charge Distribution
Atom Charge
N -0.295
C -0.483
H 0.269

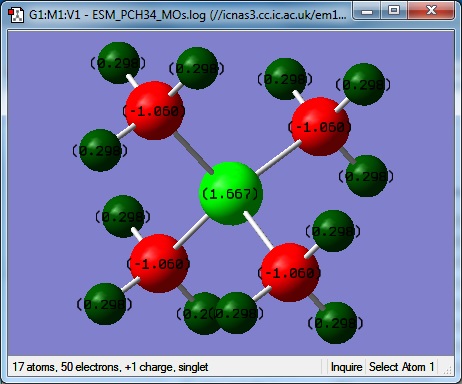
[P(CH3)4]+

Optimisation 2

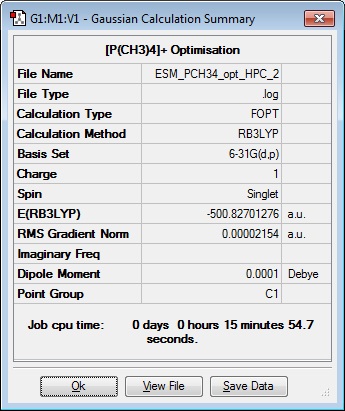
The calculation was submitted to the HPC with the same method and job type as before, but it was not optimised. To try and obtain an optimised molecule, the 'Use tight convergence criteria' was unticked, and 'scf=conver=9' was removed from the Additional keywords. The calculation was then resubmitted to the HPC. 

        Item               Value     Threshold  Converged?
Maximum Force            0.000012     0.000015     YES
RMS     Force            0.000004     0.000010     YES
Maximum Displacement     0.000772     0.000060     NO 
RMS     Displacement     0.000192     0.000040     NO 
Predicted change in Energy=-4.091175D-09
First Optimisation without tight convergence criteria or 'scf=conver=9'
Results Summary Converged? Jmol
Item Value Threshold Converged? 
Maximum Force            0.000131     0.000450     YES
RMS     Force            0.000033     0.000300     YES
Maximum Displacement     0.000931     0.001800     YES
RMS     Displacement     0.000292     0.001200     YES
Predicted change in Energy=-1.665325D-07
Optimization completed.
   -- Stationary point found. |

First Optimisation file here

This file was resubmitted to the HPC with the 'tight convergence criteria' ticked and Additional keywords 'scf=conver=9', but this did not optimise. As the above optimisation did converge, this file was submitted for frequency analysis to see if the low frequencies were within ± 20 cm-1. (This showed that the low modes were sufficiently low to continue, so bond lengths and angles are shown below.)

Bond Lengths
Bonds Length (Å)
P-C 1.82
C-H 1.09
Bond Angles
Bonds Angle (°)
P-C-H 109.9
C-P-C 109.5
H-C-H 109.0
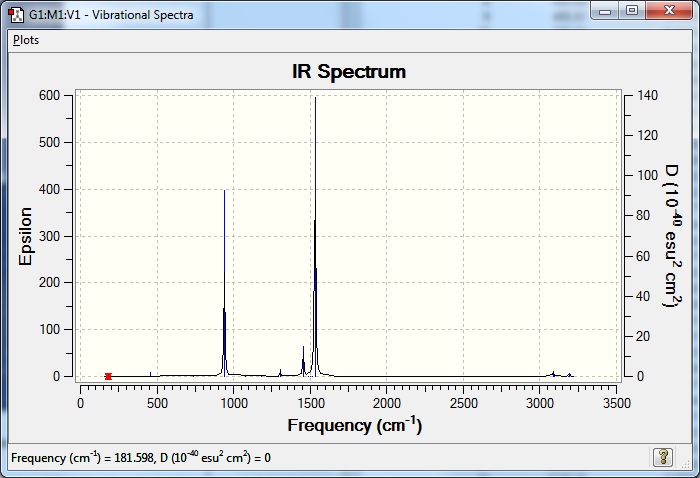
Frequency Analysis 2
Frequency Analysis from First Optimisation without tight convergence criteria or 'scf=conver=9'
Results Summary Low Modes
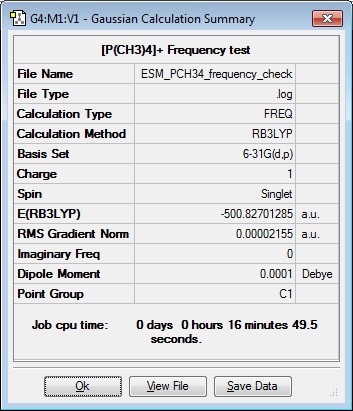Low frequencies --- -0.0030 -0.0028 -0.0023 7.6601 8.5744 16.8024 
Low frequencies ---  157.2430  191.9209  192.5722

Frequency file: DOI:10042/101843

Vibrations and IR spectrum included below

MO and NBO 1

DOI:10042/101928

Colour range from -1.000 to +1.000

[P(CH3)4]+ Charge Distribution
Atom Charge
P 1.67
C -1.06
H 0.30

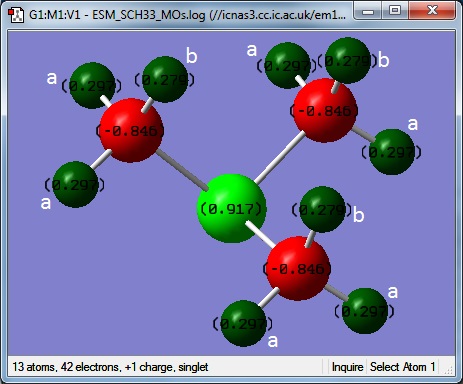
[S(CH3)3]+

Optimisation 3

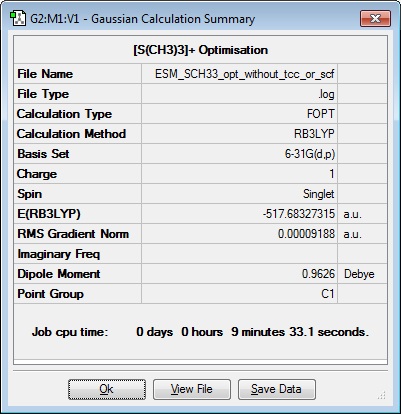
The calculation was submitted to the HPC with the same method and job type as before, but it was not optimised. To try and obtain an optimised molecule, the 'Use tight convergence criteria' was unticked, and 'scf=conver=9' was removed from the Additional keywords. The calculation was then resubmitted to the HPC.


First Optimisation without tight convergence criteria or 'scf=conver=9'
Results Summary Converged? Jmol
Item Value Threshold Converged? 
Maximum Force            0.000131     0.000450     YES
RMS     Force            0.000060     0.000300     YES
Maximum Displacement     0.001344     0.001800     YES
RMS     Displacement     0.000486     0.001200     YES
Predicted change in Energy=-6.160615D-07
Optimization completed.
   -- Stationary point found.|

Optimisation file here: DOI:10042/101894

Showing the different hydrogens specified in bond lengths and angles tables


Bond Lengths
Bonds Length (Å)
S-C 1.82
C-H 1.09
Bond Angles
Bonds Angle (°)
S-C-Ha 107.2
S-C-Hb 110.6
C-S-C 102.8
Ha-C-Ha 109.4
Ha-C-Hb 111.1
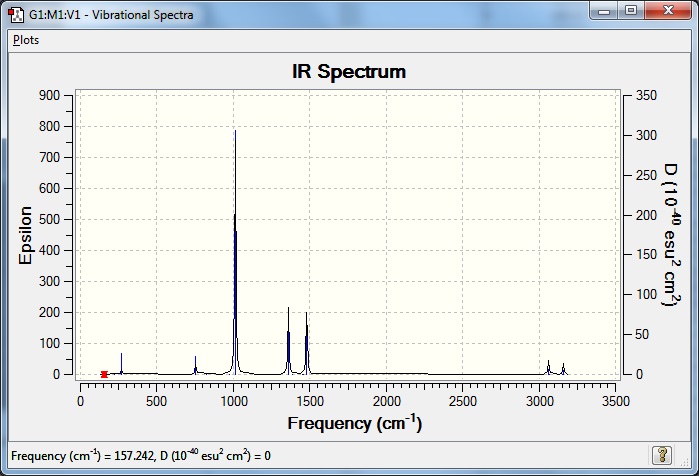
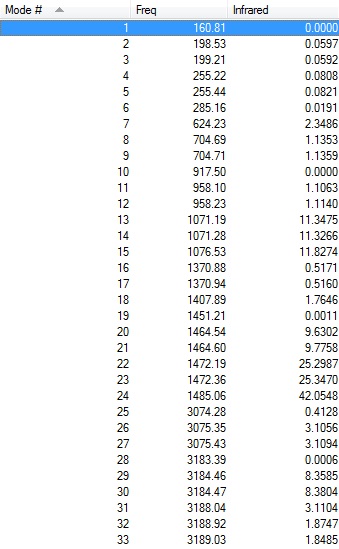
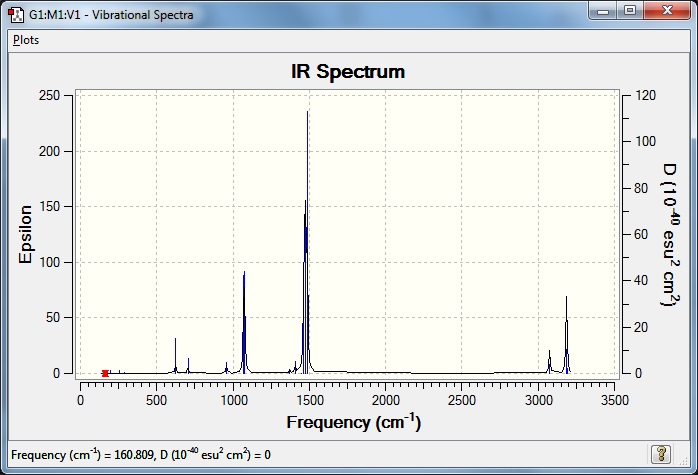
Frequency 3
Frequency Analysis from Optimisation without tight convergence criteria or 'scf=conver=9'
Results Summary Low Modes
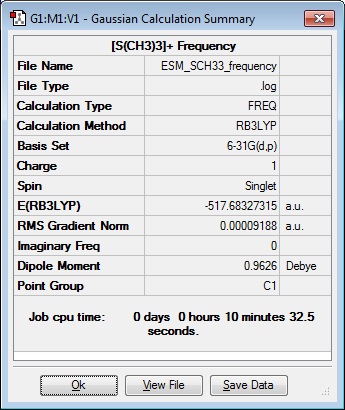Low frequencies --- -12.7228 -11.2286 -10.2109 -0.0024 -0.0010 0.0014 
Low frequencies ---  160.8097  198.5309  199.2147

Frequency file: DOI:10042/101938

Vibrations and IR spectrum shown below:

MO and NBO 2

DOI:10042/101987

Colour range from -1.000 to +1.000

[S(CH3)3]+ Charge Distribution
Atom Charge
S 0.92
C -0.85
Ha 0.30
Hb 0.28

Discussion 1

The geometries of the three different cations are comparable, showing either tetrahedral or pseudotetrahedral (in the case of [S(CH3)3]+) geometry. The bond angles in the tetra-subtituted cations are very similar, averaging around 109°. This is slightly different in the [S(CH3)3]+, where the two lone pairs on the sulphur have distorted the C-S-C angle and made it smaller, this has also had a slight effect on the S-C-H and H-C-H angles. The bond lengths are very similar for C-H, showing that those bonds are not strongly affected by the central atom. However the C-N bond length is shorter than the C-P and C-S bond lengths. This can be rationalised due to the C-N orbitals being more closely matched in energy, thus the bonding interaction between them being lower in energy and thus obtaining a stronger, shorter bond. This is also simply due to the atomic radii of N being smaller than that of P or S because it is in the row above them on the Periodic Table, and consequently has far fewer core electrons.

Charges to compare
[N(CH3)4]+ [P(CH3)4]+ [S(CH3)3]+
Atom Charge Atom Charge Atom Charge
N -0.30 P 1.67 S 0.92
C -0.48 C -1.06 C -0.85
H 0.27 H 0.30 Ha 0.30
Hb 0.28

As can be seen from the table above, directly comparing these three cations shows a significant difference in the charge distribution over the constituent atoms. In the periodic table, out of the atoms present in the cations, Nitrogen is the most electronegative, having a Pauling electronegativity of 3.04, Carbon is 2.55, Phosphorus is 2.19 and Sulphur is 2.58, Hydrogen is 2.20.1 Qualitatively this means that the expectation is that in a general comparison, electron density would be higher around N, then C, followed by P, S and then H. With the hydrogen atoms, this is seen for all the cations, as they all have a positive charge. Comparing the three heteroatoms does show the predicted trend in the sense that P has the most positive charge, S is still positive, but N is displaying negative charge. Firstly, it is easier to separate the three cations into those which show positive charge residing on the heteroatom and hydrogens. This is what would be expected as the heteroatom is accommodating an extra substituent, bonded to it by a pair of electrons donated from the heteroatom. In the case of the tetramethyl ammonium, however, the nitrogen atom shows some negative charge, at odds with the standard structure with a formally positive charge on the nitrogen. This calls into question a method to visualise charge that is commonplace, where the positive charge represents an ‘extra’ bond to the nitrogen, formed from the nitrogen’s lone pair of electrons donating as opposed to a covalent bond formed from one electron from each. However, it can firstly be rationalised that as it is common knowledge that nitrogen is a fairly electronegative atom, it is illogical to assume that the negative charge would not sit on it. Secondly, molecular orbital theory allows us to see that molecular charge can be distributed over the entirety of a molecule.[7] So a final question remains of whether or not it is possible to have charge localised in more than one site rather that a total delocalisation or an individual localisation.[7] From the data presented by the HPC calculation, it is clear that the localisation of charge on more than one site is possible and does occur, and in the case of the tetramethylammonium, this is on the hydrogen atoms. This is very simply rationalised by the hydrogens being the most electropositive atoms in the whole molecule and also having two relatively much more electronegative types of atom in the rest of the cation. However, it is important to note that all of these computational calculations are carried out in an impossible situation of having a single, isolated molecule in the gas phase, whereas in reality, especially for this discussion- examining ionic liquids- makes the argument less relevant as the behaviour of the electrons, and their localisation would be heavily influenced by the surrounding charges on other cations and anions in the bulk liquid surrounding the molecule under scrutiny.

Contrasting and comparing the C-X bond: The C-X bond in the case of trimethylammonium is composed of a third C-based orbitals and two thirds N-based orbitals. Of those orbitals, the N-based ones are sp3 while the C-based orbital contribution is not quite sp3 as it is roughly 20% s orbital with about 80% p orbital, this could be described as sp4 but this is only describing the character of the hybrid orbital and is not implying contribution from one s and four p orbitals. The reason for the higher contribution of the N to the bond is that the N sp3 orbital is lower in energy that the Carbon ‘sp4’ orbital because all these orbitals are made up of 2s and 2p, but N is more electronegative, therefore it is closer in energy to the bonding orbital created, so will have a higher contribution. This form of orbital contribution demonstrates that the use of hybridisation of orbitals is only useful up to a point, beyond which, naming the orbitals as being of a certain hybridisation confuses reality with an impossible idea of having more than 3 p orbitals. The C-P bond is split roughly 60:40 C:P orbital contribution and both of the C:P orbitals are 25% s and 75% p, implying this is the result of the combination of two sp3 orbitals. Carbon has a higher contribution to this bond because the Carbon is more electronegative than the Phosphorus and so the orbital energy is closer to the energy of the created bonding orbital. The C-S bond is comprised of almost exactly equal contributions from a C ‘sp4’ orbital and an s orbital of 17% s-character and 82% p-character. The reason for the almost equal contribution is that the electronegativities of Carbon and sulphur are almost very similar.

Influence of Functional Groups

[[N(CH3)3(CH2OH)]+

Optimisation 4
First Optimisation without tight convergence criteria or 'scf=conver=9'
Results Summary Converged? Jmol 
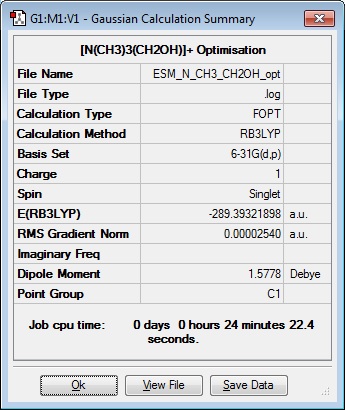        Item               Value     Threshold  Converged?
Maximum Force            0.000071     0.000450     YES
RMS     Force            0.000014     0.000300     YES
Maximum Displacement     0.001783     0.001800     YES
RMS     Displacement     0.000528     0.001200     YES
Predicted change in Energy=-8.466876D-08
Optimization completed.
   -- Stationary point found.|

Optimisation file: DOI:10042/104287


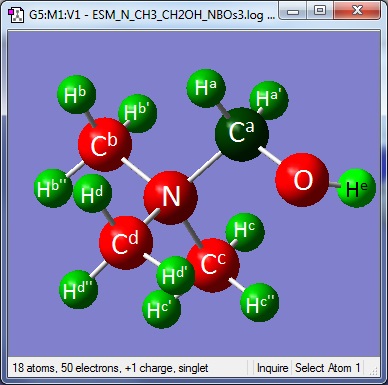
Frequency analysis on the optimised file showed that there was one imaginary frequency. In order to try and remove this the optimisation was carried out again having moved the hydrogen bonded to the oxygen out of the way of the steric bulk of hydrogens on the adjacent carbon. (Illustrated below) 


Low frequencies --- -124.0670   -6.4197   -3.3497   -0.9683   -0.0004    0.0009
Low frequencies ---    0.0012  129.2192  217.0877

Note hydrogen 'stuck' between the two hydrogens on adjacent carbon Note hydrogen being rotated outside the hydrogens on adjacent carbon

Bond lengths
Bond Length (Å)
O-H 0.97
Ca-O 1.37
Ca-N 1.55
Cb-N Cc-N 1.50
Cd-N 1.51
C-H 1.09
Bond angles
Bond Angle (°)
C-O-H 111.4
Ha-Ca-O 109.9
Ha'-Ca-O 114.7
Ha-Ca-Ha' 110.3
Ha-Ca-N 105.0
Ha'-Ca-N 106.0
Hb-Cb-Hb' 110.1
Frequency Analysis 4

Having made the adjustments described above in Optimisation, the following frequency data was returned by the HPC:

Frequency Analysis from Optimisation without tight convergence criteria or 'scf=conver=9'
Results Summary Low Modes 
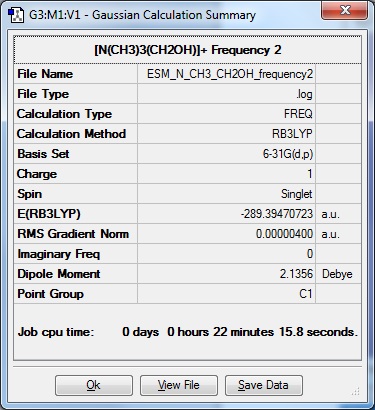Low frequencies ---   -8.2301   -4.9416   -1.5270   -0.0004    0.0011    0.0013
Low frequencies ---  131.1457  213.4545  255.7298

Frequency file: DOI:10042/104462

MO and NBO 4

DOI:10042/104504

Charge distribution, colour range from -0.400 to +0.400

Charge Distribution
Atom Charge
Ha 0.25
Ha' 0.24
Hb Hb' Hb'' 0.27
Hc 0.26
Hc' Hc'' 0.27
Hd Hd'' 0.27
Hd' 0.28
He 0.52
Ca 0.10
Cb -0.49
Cc -0.49
Cd -0.49
N -0.32
O -0.73

[[N(CH3)3(CH2CN)]+

Optimisation 5

The first optimisation was carried out using basis set 6-31G(d,p) but this did not optimise. So a lower basis set (3-21G) was used to see if a more approximate optimisation which could then be optimised further was possible. However, this did not work on the machine. So the non-fully optimised 6-31G(d,p) file was resubmitted to the HPC to see if that would return an optimised file, this was the resultant file:

Second Optimisation without tight convergence criteria or 'scf=conver=9'
Results Summary Converged? Jmol
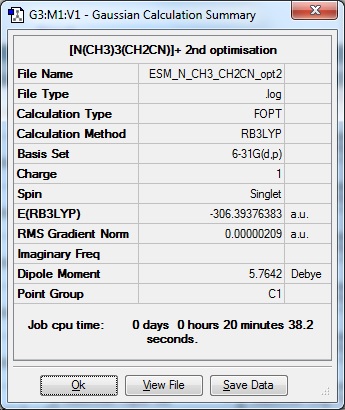Item Value Threshold Converged? 
Maximum Force            0.000010     0.000450     YES
RMS     Force            0.000001     0.000300     YES
Maximum Displacement     0.000183     0.001800     YES
RMS     Displacement     0.000043     0.001200     YES
Predicted change in Energy=-5.062846D-10
Optimization completed.
   -- Stationary point found.|

Optimisation file: DOI:10042/110749

To help with visualising the tables on the left
Bond lengths
Bond Length (Å)
Ce-Ne 1.16
Ce-Ca 1.46
Ca-N 1.53
Cb-N Cc-N Cd-N 1.51
C-H 1.09
Bond angles
Bond Angle (°)
Ca-Ce-Ne 178.8
Ha-Ca-Ce 110.4
Ha-Ca-Ha 108.7
Ha-Ca-Ha' Hc-Cc-Hc'' Hd-Cc-Hd'' 110.3
Ha-Ca-N 107.8
Ca-N-Cb 108.0
Cb-N-Cc Cb-N-Cd Hb-Cb-Hb' 110.0
Cc-N-Cd 109.6
Ca-N-Cc Ca-N-Cd 110.1
Frequency Analysis 5
Frequency Analysis from Optimisation without tight convergence criteria or 'scf=conver=9'
Results Summary Low Modes 
Low frequencies ---   -2.5042   -0.0002    0.0007    0.0008    7.2177    9.7775
Low frequencies ---   91.7854  154.0370  210.9348

Frequency file: DOI:10042/104439

MO and NBO 5

Energy file here: DOI:10042/104481

Charge Distribution, Color range: -0.489 to +0.489

Charge Distribution
Atom NBO Charge
Ha 0.31
Hb 0.27
Hb' 0.28
Hc Hc' Hd Hd' 0.27
Hc'' Hd'' 0.28
Ca -0.36
Cb -0.49
Cc -0.49
Cd -0.49
Ce 0.21
N -0.29
Ne -0.19

Discussion 2

While the earlier charge distribution visualisations were done with different colour ranges so that the atom type would be easily visible, these three have all been done with a collour range os -1.000 to +1.000 in order to be able to directly compare the charge distribution. The results have also been tabulated to show the numerical values clearly.

Charge Distribution Over Cations
[N(CH3)4]+ [N(CH3)3(CH2OH]+ [N(CH3)3(CH2NH]+
Atom Charge Atom Charge Atom Charge
H 0.27 Ha 0.25 Ha 0.31
Ha’ 0.24
Hb 0.27
Hb Hb’ Hb’’ 0.27 Hb’ 0.28
Hc 0.26 Hc Hc’ Hc’ Hd Hd’ 0.27
Hc’ Hc’’ Hd Hd’’ 0.27 Hc’’ Hd’’ 0.28
Hd’ 0.28
He 0.52
C -0.48 Ca 0.1 Ca -0.36
Cb,c,d -0.49 Cb,c,d -0.49
Ce 0.21
N -0.30 N -0.32 N -0.29
Ne -0.19
O -0.73

Comparing the Charge distribution as affected by the substituent groups

As –OH is an electron donating group and –CN is an electron-withdrawing group, the effect of this has been to reverse the charge on the carbon bonded to the substituent. The carbon in bold in [N(CH3)3(CH2OH)]+ has a slightly positive charge, showing that a lone pair of electrons on the O could donate into it, while the carbon in bold in [N(CH3)3(CH2CN)]+ has negative charge, and the underlined carbon is positively charged, showing that on a bond cleavage between the two carbons, the electrons would be attracted to the C and thereby form the -CN anion. The effect of charge distribution can have a big effect on the properties of an ionic liquid; if charge is localised in one place on the molecule, then hydrogen bonding will occur and anions will be held in a more ordered fashion around the caiton. If, however, the charge is more dispersed across the molecule, then the anions will not be in as rigid a solvation shell around the cation, thus the diffusion constant would be lower and the cohesive energy would be higher.[8]


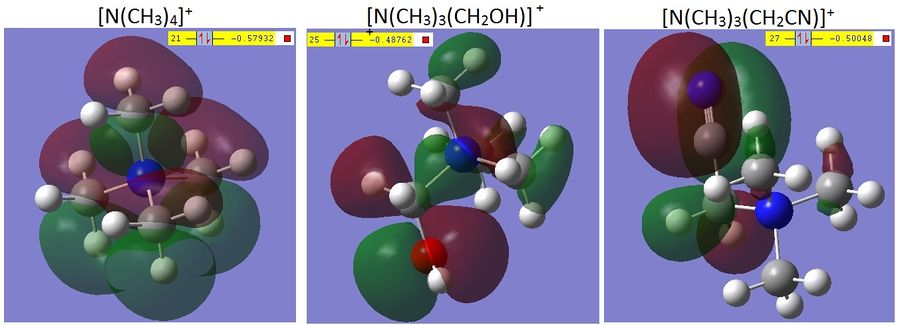
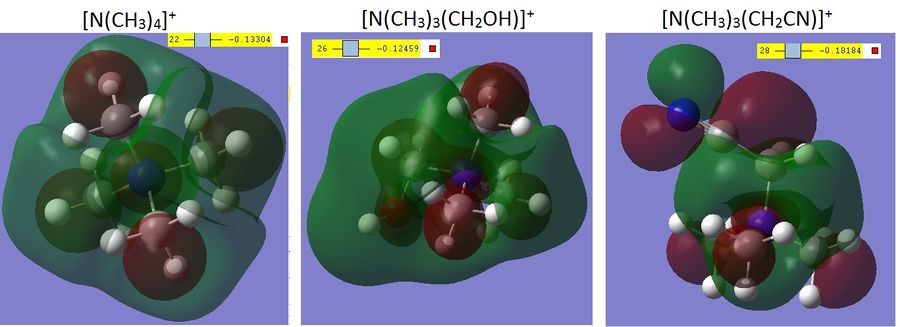
Comparing the MOs for trimethylammonium and with different FGs

The shape of the HOMOs of each of the cations changes significantly going from simple trimethylammonium and then adding functional groups to one of the methyl substituents. First to note is that the HOMO of the trimethylammonium is quite symmetrical (the point group was not set in any of these calculations to avoid the calculations taking too many steps and failing to optimise) and the orbital is delocalised over the majority of the molecule. Contrast this with the [N(CH3)3(CH2OH)]+ where the roughly a third of the HOMO is an p-orbital on the O, interacting with the adjacent C-H σ-bond, and the [N(CH3)3(CH2CN)]+ where over half of the orbital is the C-N π orbital, with a very slight interaction with two C-H σ-bonds. It is possible to see too that the relative energy of the HOMOs is (in order of increasing stability) [N(CH3)3(CH2OH)]+ < [N(CH3)3(CH2CN)]+ < [N(CH3)4]+. This is partly due to the loss of symmetry going from the [N(CH3)4]+ and adding the nitrile group, which reduces the rotational symmetry, and then substituting for the hydroxyl group which, due to the location of the O-H bond is totally unsymmetrical. Furthermore the HOMO, as defined by Gaussian, on the [N(CH3)4]+ has two other degenerate orbitals, both of which also display the high level of dissociation of the first one mentioned. This is not the case for the other two cations, although there are MOs with similar levels of energy according to Gaussian, the degeneracy is lost, again due to the loss of symmetry.

The LUMOs of each of the cations all show a high level of dissociation over the molecules, but the nitrile group shows a relatively non-interacting p-like-orbital separate from the rest of the delocalisation, while the orbitals on the oxygen are highly interacting with the rest of the delocalised orbital, this implies that the reactivity of the LUMO of the nitrile cation is higher than that of the hydroxy-cation and the trimethylammonium is much more stable than both of them.

The HOMO-LUMO gaps of the molecules in order of increasing size is [N(CH3)3(CH2CN)]+ < [N(CH3)3(CH2OH)]+ < [N(CH3)4]+. This indicates that the reactivity of the cations is subsequently in the reverse order as a large HOMO-LUMO gap indicates kinetic stability.[9]

The implication of this in the context of ionic liquids is that in order to obtain a higher melting-point liquid, [N(CH3)4]+ would be better than the other two cations because it would be less likely to form a solid at a given temperature as the dipole is less and so dipole-induced-dipole interactions would be kept to a minimum, and the overall interaction between the cation and a given anion would be less favoured than with the other two cations.

References

  1. ↑ 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press, 9th Editio., 2012.
  2. ↑ S. Batsanov and A. Batsanov, Introduction to Structural Chemistry, Springer, 2012.
  3. ↑ Gaussview 5 Reference. Rebonding Structures. http://www.gaussian.com/g_tech/gv5ref/build.htm. Last edited 22/05/14. Accessed:18/11/14
  4. ↑ C.-A. Chang, J. Phys. Chem., 1983, 87, 1694–1696.
  5. ↑ R. M. Badger, J. Chem. Phys., 1935, 3, 710–714.
  6. ↑ 6.0 6.1 M. Freemantle, An Introduction to Ionic Liquids, The Royal Society of Chemistry, 2010.
  7. ↑ 7.0 7.1 K. T. Lee, H. M. Kim, K. Y. Han, J. Sung, K. J. Lee, and S. K. Kim, J. Am. Chem. Soc, 2007, 129, 2588–2592.
  8. ↑ R. M. Lynden-Bell and T. G. a Youngs, J. Phys. Condens. Matter, 2009, 21, 424120.
  9. ↑ K. T. Lee, H. M. Kim, K. Y. Han, J. Sung, K. J. Lee, and S. K. Kim, J. Am. Chem. Soc, 2007, 129, 2588–2592.
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:EMorcomC1&oldid=816729"