Rep:Mod:EMERALDBAY
Thomas Arrow Physical Computational
The Cope Rearrangement
The most simplistic cope rearrangement is studied in order to determine whether a chair or boat transition state is more facile. This reaction is shown to the right.
Optimisation of Reactants and Products
A conformation of hexa-1,5-diene was optimised at the HF/3-21G level. This yielded a structure (1) with an energy of -231.69253528 Ha and Ci symmetry. It also had the bond lengths tabulated below. See to the right for a 3D model.
| Bond | Length (Å) |
|---|---|
| 1-2 | 1.32 |
| 2-3 | 1.51 |
| 3-4 | 1.55 |
| 4-5 | 1.51 |
| 5-6 | 1.32 |
A second conformation (2) of hexa-1,5-diene with the central 4 carbon atoms in a gauche configuration was optimised in the same way. It had an energy of -231.69266122 Ha and C1 symmetry. A 3D structure is available to the right.
The bond lengths are tabulated below:
| Bond | Length (Å) |
|---|---|
| 1-2 | 1.32 |
| 2-3 | 1.51 |
| 3-4 | 1.55 |
| 4-5 | 1.51 |
| 5-6 | 1.32 |
Notably they are the same (to within the nearest 0.01Å) as the anti conformation.
Unsurprisingly it appears that anti conformations are more stable than gauche conformations. This is due to both more stable steric and electronic interactions. Specifically, it reduces Pauli repulsions between the substituents and also maximizes the number of C-Hσ/C-Hσ* interactions which are medium energy donor and acceptor orbitals compared to the sum of C-Hσ/C-Cσ* (which are strong) and the C-Cσ/C-Hσ* (which are very weak) interations.
We can undertake a similar view for the conformation of the alkene groups which are most stable aligned in an eclipsed form due to strong C-Hσ/C-Cπ* interactions.
This means that structure 1 is likely to have the lowest energy conformation. This is indeed the case and is in accordance with the range of different conformations in Appendix 1 of the script.
Optimisation + Frequency Calculation with a better basis set
We therefore wish to study in detail structure 1. This is done with a B3LYP method at the 6-31-d level. This resulted in a structure (3) with an energy of -234.61170161 Ha and Ci symmetry. A frequencies calculation was undertaken at the same time. It can be shown that this structure is a minimum because there are no imaginary frequencies (i.e. with a frequency below 0±20cm-1). We can see the from the Low Frequencies line of the log file which is pasted below:
Low frequencies --- -19.9763 -11.5610 -2.0650 -0.0008 0.0006 0.0007 Low frequencies --- 72.0158 77.2720 121.0841
The calculated IR spectrum is also shown right.
Also calculated are the thermochemical properties of the molecule. These are tabulated below:
| Sum of electronic and zero-point Energies | 234.469243 |
| Sum of electronic and thermal Energies | 234.461878 |
| Sum of electronic and thermal Enthalpies | 234.460933 |
| Sum of electronic and thermal Free Energies | 234.500888 |
The Transition State
Optimisation to a Chair TS(Berney)
A calculation to find the structure of a maximum on the potential energy surface was performed at the HF/3-21G using gaussian. This resulted in a structure with one imaginary frequency ( at 818cm-1). This is what we would expect for a transition state. This vibration is shown below and clearly does correspond the the Cope rearrangement as we would expect with a chair TS. It has an energy of -231.61932246 Ha. It also had symmetry of C2h. There is a bond length of 2.02Å between the bond breaking/making carbons.
Optimisation to a Chair TS(Frozen Coordianate)
A similar calculation was performed at the HF/3-21G level in gaussian however the bond between the bonding carbon fragments was frozen and the rest of the molecule optimised to place it in it's most relaxed state. The molecule was then further optimised to the lowest derivative of the bond length of the C-C bonds to be made/broken. It had an energy of -231.61932160 Ha and also a symmetry of C2h.It has making/breaking C-C bond lengths of 2.02Å. This is, to within a small margin of error identical to the result found by optimising to a transition state.
It was noted that in performing this calculation some difficulties were encountered. Specifically in giving the correct ordering of inputs to gaussian's modredundant function. It appears that during the second optimisation it is necessary to pass the bond derivative setting before the bond freezing setting otherwise it simply . It is also important to set geom=modredundant which gaussview occasionally omits.
Optimisation to a Boat TS(QST2)
A structure for the boat transition state was found by the QST2 method. This simply interpolates between the two structures given for the start and end of the reaction. Initially structure 1 was used as both the initial and final state however this was found to fail because the linear interpolation between these structures is very far from the TS. It was found that by shaping both reactant and product to be more similar to the TS that this calculation then succeeded. It had an energy of -231.60280234 Ha. It has making and breaking C-C bond lengths of 2.14Å A frequency calculation was subsequently performed which found an imaginary frequency of 840cm-1. This is also equivalent to the cope rearrangement and is shown below.
IRCs of the two transitions
| Chair IRC | Boat IRC |
|---|---|
|
|
|
|
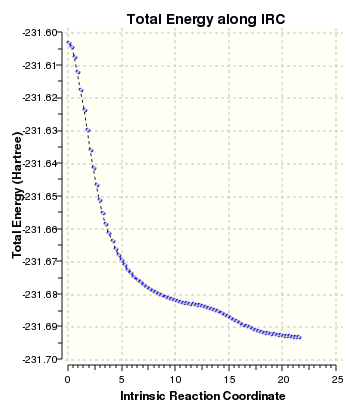
We can see that as expected both transition states decay to different confomers. The chair decays to a low energy anti conformer where as the boat decays to a higher energy gauche conformation.
Activation Energies of the Transition States
It is necessary that we calculate the ground and transition states using the same method and basis sets in order for comparisons of energy between them to be meaningful. For this reason both the chair and boat transition states were reoptimised using the 631-G(d) basis set. The difference in energy between them and the lowest ground state configuration (1) is the activation energy for the reaction. These are tabulated below:
| Structure | Electronic energy (Ha) | Electronic + Zero Point Energy (Ha) | Electronic + Zero Point + Thermal Energy (Ha) | Activation Energy (Ha) | Activation Energy (kJmol-1) |
|---|---|---|---|---|---|
| 1 | -231.69253529 | -231.539540 | -231.570911 | 0 | 0 |
| Chair TS | -231.619322457 | -231.466700 | -231.495206 | 0.075705 | 198.7634487321 |
| Boat TS | -231.457206655 | -231.450924 | -231.479770 | 0.091141 | 239.29066086642 |
| Structure | Electronic energy (Ha) | Electronic + Zero Point Energy (Ha) | Electronic + Zero Point + Thermal Energy (Ha) | Activation Energy (Ha) | Activation Energy (kJmol-1) |
|---|---|---|---|---|---|
| 1 | -234.596353743 | -234.469243 | -234.500888 | 0 | 0 |
| Chair TS | -234.554467516 | -234.414924 | -234.443810 | 0.057078 | -149.85826731036 |
| Boat TS | -234.540462012 | -234.402337 | -234.431746 | 0.069142 | -181.53229472604 |
We can see that there is a relatively large difference in the activation energies between the two levels of optimisation however the higher level one, as expected, is in better agreement with the experimental values for the activation energies of the transition states: 140kJmol-1 and 187kJmol-1 for the chair and boat respectively (As quoted from the script) This is also in the literature. [1]
Diels Alder Reactions
cis-butadiene and ethylene
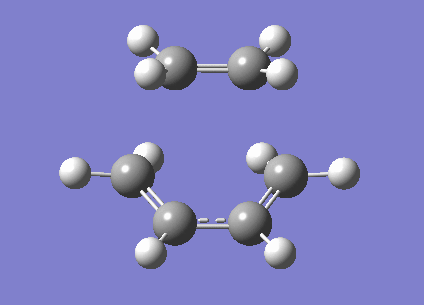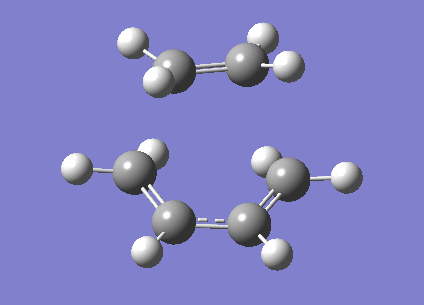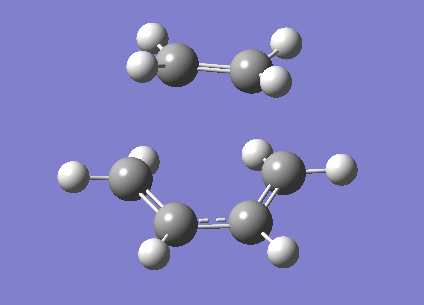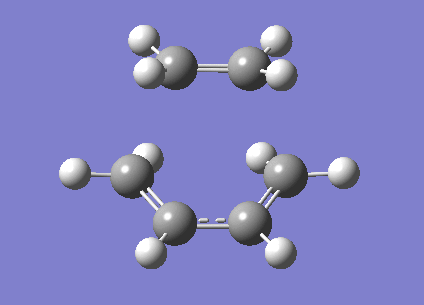
In studying diels alder reactions we shall initially study one of the most basic ones: the addition of ethylene to butadiene. This is shown to the right.
Optimisation of reactants
Optimisation for both molecules was initially performed at the AM1 semi-empirical level before further optimisation at the 6-31G(d) level. At the same time frequency calculations were performed on each molecule to shown that we had indeed found an energy minimum and not a maxima.
cis-butadiene
It was noted that initially; from drawing a planar molecule optimisation to a planar molecule resulted. However this is obviously not a realistic structure as is shown by a large imaginary frequency in its vibrational spectrum. This was corrected by altering the dihedral angle of the 4 central carbon atoms to ca. 25°
ethylene
Optimisation performed without out anything of particular note.
Structure of reactants
cis-butadiene
The structure formed is available to view in 3D to the right. The final dihedral angle of the central 4 carbon atoms was 30°, just slightly twisted. It was shown to have an energy of -155.98648969 Ha and C2 symmetry.
The HOMO and LUMO are shown in the pictures below.
| HOMO | LUMO |
|---|---|
|
|
| Clearly we can see that the wavefunction is approximately anti-symmetric with respect the plane that lies on the 4 carbon atoms (if the molecule were flat rather than slightly bent). | Here the wavefunction is symmetric wrt the same plane. |
Ethylene
The structure is available to view to the right. It had D2h symmetry and an energy of -78.58745744 Ha
| HOMO | LUMO |
|---|---|
|
|
| Clearly we can see that the wavefunction is symmetric with respect to the plane that lies perpendicular to the C=C (the only plane of symmetry in cisbutadiene). | Here the wavefunction is anti symmetric with respect to the plane. |
We expect, and indeed find that the transition state is an overlap between the LUMO of ethylene and the HOMO of butadiene.
Optimisation of Transition state
The transition state was optimised by simply placing by eye the two fragments. Freezing the two C-C bonds and optimising to a minimum. This structure was then unfrozen and optimised to a TS (berney). This was done in order to prevent it from failing to to being too far from the transition state geometry. This was done using the semiempirical/AM1 method and then further optimised using B3LYP/6-31G(d).
Structure of transition state
The structure of the transition state was found to have an energy of -234.54389743 Ha and Cs symmetry. We kniw it is a transition state because it has one and only one imaginary frequency; shown below. The length of the C-C bonds that are being formed/broken is 2.27Å. This is far longer than an normal C-C bond whether sp2 or sp3 hybridised.
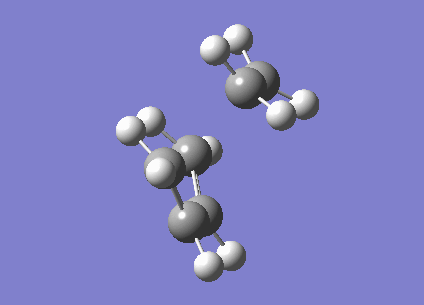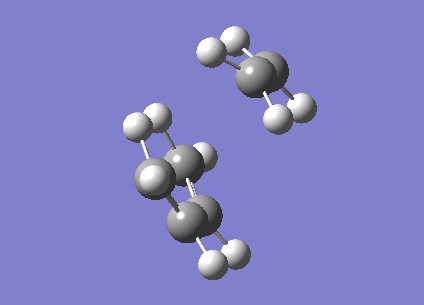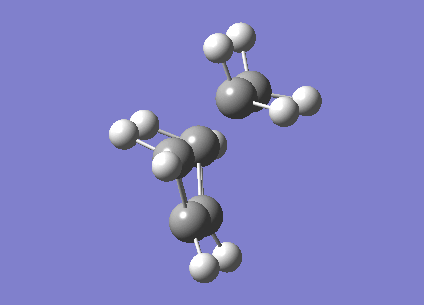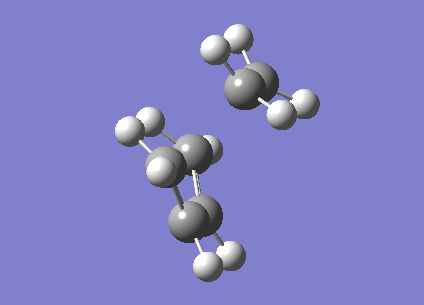
Clearly this does correspond to the Diels Alder reaction. However the first real frequency is simply a rocking mode of the molecule. It is not forming a bond asynchronously because the frequency is real. This means that exciting in this vibration results in an increase rather than decrease in energy. This is because we have not found a TS for an asynchronus reaction. This vibration is shown below.
We can also look at the HOMO and LUMO of the TS. This is shown below.
| HOMO-1 | HOMO | LUMO |
|---|---|---|
|
|
|
Oddly we would have expected a HOMO that is asymmetric with respect to the plane however this is not the picture that was calculated. However, the HOMO-1 is asymmetric and is pictured above. It is suggested that due to some calculation artifact the the energies have ended up reordered.
IRC
An IRC was also conducted using the B3LYP/6-31G(d) level of symmetry. This resulted in the curve shown below.
|
|
Activation Energy of TS
| Structure | Electronic energy (Ha) | Electronic + Zero Point Energy (Ha) | Electronic + Zero Point + Thermal Energy (Ha) | Activation Energy (Ha) | Activation Energy (kJmol-1) |
|---|---|---|---|---|---|
| cis-butadiene | -155.986165259 | -155.901143 | -155.927850 | 0 | 0 |
| ethylene | -78.5870189959 | -78.536219 | -78.557748 | 0 | 0 |
| TS | -234.541182666 | -234.403320 | -234.432889 | 0.052709 | 138.38745947058 |
Malaic Anhydride and 1,3-cyclohexadiene
Optimisation of the Reagents
Reagent optimisation was initially performed using the AM1 pesudoempirical method and then further optimised at the 6-31G(d) level. Similarly to before it was noted that a planar structure was initially drawn and then optimised for the diene structure however this is a transition state between two twisted states which are the actual low energy configuration.
Optimisation and Structure of the Endo TS
Optimisation was initially performed from an semiempirical/AM1 optimisation of a a guess transition state that was drawn by eye using the product as an initial guess. This was then further optimised at the B3LYP/6-31G(d) level. We can clearly see that this is a TS by the single imaginary frequency. This mode is shown below and is also clearly the Diels Alder reaction. It has an energy of -612.68339677 Ha and Cs symmetry. The C-C bond length that is being formed has a length of 2.27Å.
Optimisation of the Exo TS
Optimisation was again performed first with semiempirical/AM1 and then B3LYP/6-31G(d) from TS guessed by eye from the product. The single imaginary frequency proving it is a transition state is shown below. It had an energy of -612.67931096Ha and a symmetry of Cs. The C-C bond being formed ha a length of 2.29Å
IRC of the Transition States
IRCs were conducted for both these transition states at the B3LYP/6-31G(d) level.
| Endo | Exo |
|---|---|
|
|
|
|
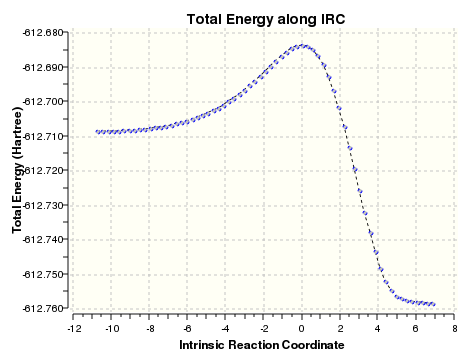
Activation Energies of TS
| Structure | Electronic energy (Ha) | Electronic + Zero Point Energy (Ha) | Electronic + Zero Point + Thermal Energy (Ha) | Activation Energy (Ha) | Activation Energy (kJmol-1) |
|---|---|---|---|---|---|
| Sum of Reactants | -233.404260793 + -379.283563366 = -612.687824159 | -233.296105 + -379.233657 = -612.529762 | -233.324356 + -379.262729 = -612.587085 | 0 | 0 |
| Endo Transition State | -612.68339677 | -612.502139 | -612.538327 | 0.048758 | 128.01411047196 |
| Exo Transition State | -612.667296928 | -612.498012 | -612.534265 | 0.05282 | 138.6788899284 |
Trivially here we can see that, as one expect experimentally, the endo form is favoured energetically. In order to investigate why we can consider the structures of the different transition states.
Geometries of the transition states
We can consider the extent of clashing of the carbon atoms in the two transition states. The distances for these are depicted below.
| Endo | Exo |
|---|---|
|
|
This however is not in accordance with what we would expect in terms of energy (because closer distances imply closer clashing) so we must consider the MO's of the transition states.
MO's of the TS
| Endo | Exo |
|---|---|
|
|
We can see that the main difference is the lack of a nodal plane, although strong decay of electron density between the Oxygen lobes and the cyclohexadiene, in the endo structure. Whereas there is a clear nodal plane in the equivalent position in the exo structure. This means that the exo MO is far less bonding and thus higher in energy. This is probably the main reason for the endo versus exo selectivity; the electronic effects outweigh the steric ones.
We conclude that not only the orbitals of the diene and the alkene matter but also the secondary orbitals located on other parts of the reactant molecules can come into play to lower the reactant energy (a secondary orbital effect).
Log Files
Provided below are log files for the key calculations in this experiment:
| Calculation | Log File |
|---|---|
| Gauche Conformation of 1,5-hexadiene | File:TAGAUCHE.LOG |
| Anti Conformation of 1,5-hexadiene | File:TAANTI.LOG |
| COPE Chair TS | File:TACHAIR.LOG |
| COPE BOAT TS | File:TABOAT.LOG |
| Simple Diels Alder TS | File:TADA.LOG |
| Endo Diels Alder TS | File:TAENDO.log |
| Exo Diels Alder TS | File:TAEXO.log |
References
- ↑ W.von E. Doering, W.R. Roth, The overlap of two allyl radicals or a four-centered transition state in the cope rearrangement, Tetrahedron, Volume 18, Issue 1, 1962, Pages 67-74, ISSN 0040-4020, http://dx.doi.org/10.1016/0040-4020(62)80025-8. (http://www.sciencedirect.com/science/article/pii/0040402062800258)