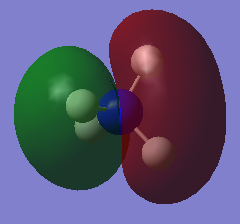Rep:Mod:EM0516
NH3
NH |
The optimisation file is liked to here
Summary of calculation
| Calculation Method | B3LYP |
| Final Energy (a.u.) | -56.55776873 |
| RMS gradient norm (a.u.) | 0.00000485 |
| Point group | C3v |
Bond length and angle
| N-H bond length (angstroms) | 1.01798 |
| H-N-H bond angle (degrees) | 105.741 |
The N-H bond length calculated is similar to the literature value 1.008 ± 0.004 angstrom.[1] The literature value of N-H-N bond angle is 106.6° which is quite similar to the calculated value.[2] I think the slight difference in the angle is due to different experimental condition. In an experiment, bond angle of an atom is determined by X-ray crystallography in its crystal lattice form whereas in Gaussview program, calculation is done on only one molecule on its own.
Optimisation table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986271D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
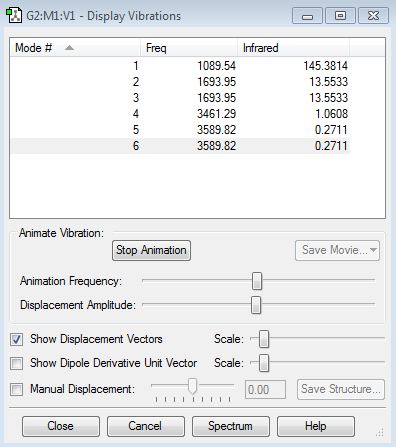
Vibrational modes
The total of 6 modes are expected from NH3 due to 3N-6 rule. (3(4)-6=6).
The degenerate modes are the modes with equivalent frequencies which are modes 2 and 3 as well as modes 5 and 6. Through modes animation it can be seen that modes 1,2 and 3 correspond to bond bending and modes 4,5 and 6 correspond to bond stretches. Also, shown in the table above, “bending” vibrations have much lower frequencies than “bond stretch” vibrations.
Mode 4 is highly symmetric as it shows symmetrical stretching of all three N-H bonds. Mode 1 shows bending of three bonds in inward direction altogether. This mode of bending is known as “umbrella” mode. This is because the movement of bonds are similar to that of putting down an umbrella.
There will be only three bends in IR spectrum of gaseous ammonia, one of them being mode 2 and another, mode 6. The mode 2 and 3 are degenerate so there’s only one bend indicating these degenerate modes. Also, bend from mode 4 (bond-stretch) will be shown but in much smaller peak. This is because the vibrations that causes change in the dipole moment will be detected in IR spectrum and bond-stretch vibrations do not cause much change in dipole moment as bending vibrations do. Furthermore, symmetric stretch and bending vibrations are IR inactive.
]
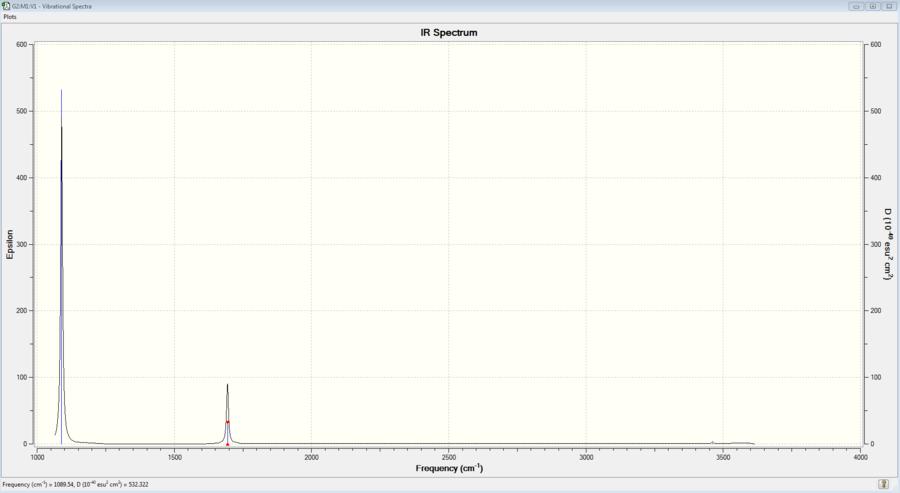
This is the IR spectrum of optimised NH3 molecule. As expected from the frequency values a strong peak is observed at 1089cm-1(mode 1 vibration) and the next peak is observed at 1693.95cm-1 (Modes 2 and 3) with less intensity than that of Mode 1. Also, there's very small peak observed at 3461.29cm-1 which is Mode 4 (bond stretch vibration).
Above is the experimental IR spectrum of ammonia. The peak around 3100-3400cm-1 indicates N-H bond stretches and the other peak at around 1550-1640cm-1 indicates N-H bond bending.[4] The number of peaks and wavelength values match with the theoretical IR spectrum of Gaussview. The difference between these two spectra is fine structure: it is only present in the experimental spectrum.
Charge distribution
As shown in the diagram, N has charge of -1.125 and H has +0.375.
Ammonia is a neutral molecule with polar covalent N-H bonds. Negative charge is expected around N atom, as nitrogen is electronegative, bigger electron density is on nitrogen, making its charge negative. Also, as ammonia is a neutral molecule, 3 H atoms add up to the same charge magnitude but the charge is positive to make the overall charge of the molecule 0.
N2
N2 |
The optimisation file is liked to here
Summary of calculation
| Calculation Method | B3LYP |
| Final Energy (a.u.) | -109.52412868 |
| RMS gradient norm (a.u.) | 0.00000060 |
| Point group | D∞h |
Bond length
| N-N bond length (angstroms) | 1.10550 |
This optimised result of N-N bond length matches with the literature value which is 1.0975 ± 0.0001 angstrom. [1]
Optimisation table
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.401106D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
-------------------------------------------------------------------
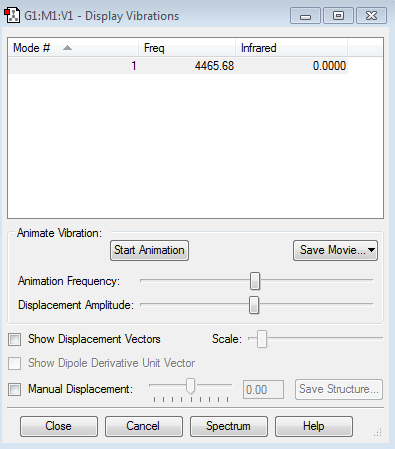
Vibrational modes
There's only one vibrational modes shown in N2. As N2 is a linear molecule, only N-N triple bond stretch is shown. There is no value on infrared table as N2 goes through symmetric stretch thus its vibrational mode is IR inactive.
Molecular orbital
| HOMO | LUMO |
|
|
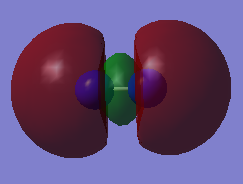
H2
H |
The optimisation file is liked to here
Summary of calculation
| Calculation Method | B3LYP |
| Final Energy (a.u.) | -1.17853936 |
| RMS gradient norm (a.u.) | 0.00000017 |
| Point group | D∞h |
Bond length
| N-N bond length (angstroms) | 0.74279 |
Optimisation table
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Vibrational modes
Molecular orbital
| HOMO | LUMO |
|
|
H2 is homonuclear diatomic molecule. Just like N2, H2 only has symmetric bond stretch thus hydrogen atom's vibration is IR inactive.
Haber-Bosch Reaction Energy
This is the chemical equation for Haber-Bosch process. N2 + 3H2 -> 2NH3
The energy values of the table below are in a.u.
| E(NH3) | -56.55776873 |
| 2*E(NH3) | -113.11553746 |
| E(N2) | -109.52412868 |
| E(H2) | -1.17853936 |
| 3*E(H2) | -3.53561808 |
| ΔE=2*E(NH3)-[E(N2)+3*E(H2)] | -0.055791 |
ΔE= -0.055791a.u.= -146.478kJ/mol -> -146.49kJ/mol (2 d.p.)
Negative ΔE indicates that energy is released in this reaction thus, this is a spontaneous reaction. The ammonia product is lower in energy than the reactants, therefore the reaction will favour the production of ammonia.
The literature value of enthalpy of formation of ammonia is -92kJ/mol.[5] The theoretical enthalpy and the experimental enthalpy is quite different due to difference in conditions. The the enthalpy of formation of ammonia is calculated in a condition similar to vaccum, where there's only one molecule in an empty space. Also, temperature is not taken into account. On the other hand, the experimental enthalpy is calculated in a condition which is 400-450°C, 200 atm in presence of iron catalyst. Also both reactants were in it gaseous state. Such difference in reaction condition has resulted in difference in enthalpy values.
NH4+ ion
NH |
The optimisation file is liked to here
Summary of calculation
| Calculation Method | B3LYP |
| Final Energy (a.u.) | -56.90586436 |
| RMS gradient norm (a.u.) | 0.0001191 |
| Point group | Td |
Bond length and angle
| N-H bond length (angstroms) | 1.02761 |
| H-N-H bond angle (degrees) | 109.471 |
The N-H bond length is similar to the literature value 1.031 ± 0.004 angstrom.[1]
H-N-H bond angle comparison between NH3 and NH4+
| H-N-H bond angle (degrees) | |
| NH3 bond angle | 105.741 |
| NH4+ bond angle | 109.471 |
Both molecules have the same tetrahedral pseudostructure. In case of NH3, its actual structure is trigonal pyramidal with 3 N-H bonds and one lone pair. NH4+ has tetrahedral structure with 4 N-H bonds and no lone pairs. The difference in angle of these two molecules can be explained by Valence Shell Electron Pair Repulsion (VSEPR) theory. According to the theory lone pair- bond pair repulsion is stronger than bond pair-bond- pair repulsion. In NH3 lone pair- bond pair repulsion is present, thus hydrogen atoms in NH3 is pushed down more than bond pair-bond pair repulsion. This explains smaller bond angle in NH3 than that of NH4+. In case of NH4+, there's no lone pair-bond pair repulsions but only bond pair-bond pair repulsions. Therefore hydrogen atoms in NH4+ experience less repulsion than that of NH3 atoms and has larger bond angle.
Optimisation table
Item Value Threshold Converged?
Maximum Force 0.000232 0.000450 YES
RMS Force 0.000124 0.000300 YES
Maximum Displacement 0.000537 0.001800 YES
RMS Displacement 0.000287 0.001200 YES
Predicted change in Energy=-2.494883D-07
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,5) 1.0276 -DE/DX = -0.0002 !
! R2 R(2,5) 1.0276 -DE/DX = -0.0002 !
! R3 R(3,5) 1.0276 -DE/DX = -0.0002 !
! R4 R(4,5) 1.0276 -DE/DX = -0.0002 !
! A1 A(1,5,2) 109.4712 -DE/DX = 0.0 !
! A2 A(1,5,3) 109.4712 -DE/DX = 0.0 !
! A3 A(1,5,4) 109.4712 -DE/DX = 0.0 !
! A4 A(2,5,3) 109.4712 -DE/DX = 0.0 !
! A5 A(2,5,4) 109.4712 -DE/DX = 0.0 !
! A6 A(3,5,4) 109.4712 -DE/DX = 0.0 !
! D1 D(1,5,3,2) -120.0 -DE/DX = 0.0 !
! D2 D(1,5,4,2) 120.0 -DE/DX = 0.0 !
! D3 D(1,5,4,3) -120.0 -DE/DX = 0.0 !
! D4 D(2,5,4,3) 120.0 -DE/DX = 0.0 !
-------------------------------------------------------------
Charge distribution
Just like ammmonia, nitrogen has negative charge due to its high electonegativity. The nitrogen atom pulls electron density from N-H covalent bonds towards itself. An ammonium ion has overall charge of +1, therefore hydrogens have positive chrages that adding up charges of nitrogen and 4 hydrogen atoms give a value of +1.
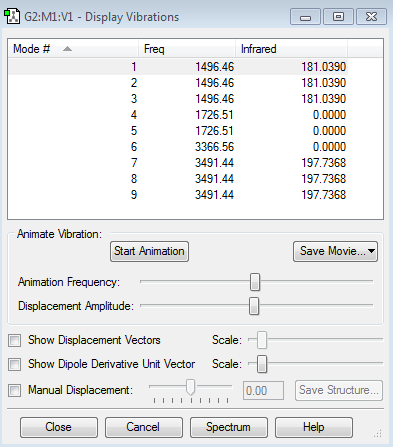
Vibrational Modes
There are 9 modes of vibration which can be predicted from 3N-6 rule. Modes 1 to 5 indicates bending vibrations and modes 6 to 9 indicates bond stretches. There are only 2 vibrations that are IR active, Mode 1 (which has the same frequency as modes 3 and 4 thus degenerate) and Mode 7 (which is denerate). Unlike ammonia, the bond stretch vibration has stronger IR intensity than that of bond bending vibration. In this case, bond stretch results in greater change in dipole moment than bond bending vibrations. Again, modes 4,5 and 6 are not IR active as those are symmetric bending and stretch vibrations.
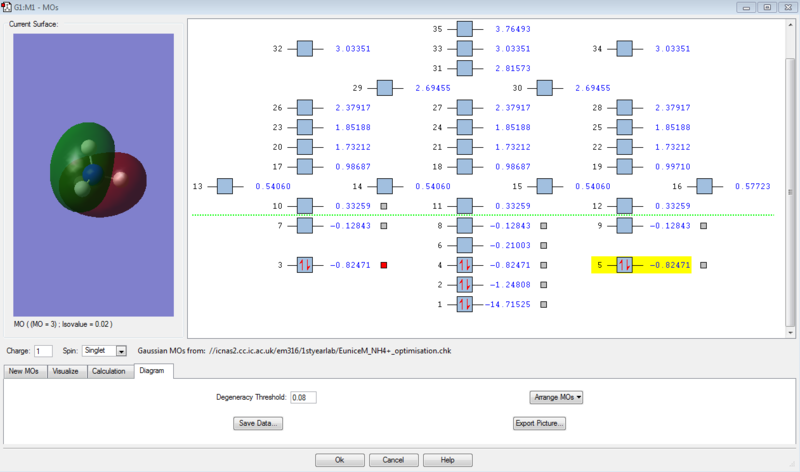
Molecular Orbitals
| MO | |
|
MO 1
This MO represents none bonding. The electron density is concentrated around N atom and there's no bonds formed. |
|
MO 2
This is a filled orbital with deepest energy of -1.24808 a.u. The 2s atomic orbital from nitrogen and 1s atomic orbital from hydrogen contribute in MO. |
|
MO 3
This is HOMO (highest occupied molecular orbital) with energy of -0.82471 a.u. A 2p atomic orbital of nitrogen and 1s atomic orbital of hydrogen contribute in this MO. There are 3 degenerate MOs which are 2px, 2py and 2pz atomic orbitals of N contributing. |
|
MO 4
This is the degenerate MO. This MO has the same energy as HOMO, which is 0.82471 a.u. |
|
MO 6
This is LUMO (lowest unoccupied molecular orbital) with energy of -0.21003 a.u. The 2s atomic orbital of nitrogen and 1s atomic orbital of hydrogen contribute in this MO. On the other hand, this shows antibonding character as the phase of nitrogen's s orbital and hydrogen's s orbital are different. |
This the MO diagram of NH4+ atom. As shown in the diagram, MO 1 is deepest in the energy and MO 3,4,5 is aligned to show degeneracy. The MOs after beyond LUMO is not included as there's no electrons in those MOs, the MO diagram is not accurate.
Reference
- ↑ 1.0 1.1 1.2 http://www.wiredchemist.com/chemistry/data/nitrogen-compounds
- ↑ https://winter.group.shef.ac.uk/vsepr/NH3.html
- ↑ http://webbook.nist.gov/cgi/cbook.cgi?ID=C7664417&Type=IR-SPEC&Index=1
- ↑ P. Atkins and J. De Paula, Atkins’ physical chemistry, 2009.
- ↑ http://www.chemguide.co.uk/physical/equilibria/haber.html