Rep:Mod:EL16121C

Introduction

The aim of the first part of this experiment was to predict the regioselectivity of the hydrogenation of an unsubstituted cyclopentadiene dimer using molecular mechanics. The geometry and the energy of an intermediate in the synthesis of taxol were also optimised using molecular mechanics. The ¹H NMR and ¹³C NMR of a derivative of this intermediate was predicted using quantum mechanics. The results where then compared with the literature to investigate whether the optimised conformer was of the correct conformation.

The aim of the second part of this experiment was to find and comment on the crystal structure of the Shi and the Jacobsen catalysts. The two enantiomers of the epoxides of 1,2-dihydronaphthalene and trans-β-methylstyrene were pre-optimised using molecular mechanics and then optimised using quantum mechanics. The optical rotation and the VCD, ¹H NMR and ¹³C NMR spectra of the epoxides was computed and compared with the literature. The enantiomeric excess obtained when epoxidising 1,2-epoxy-1,2,3,4-tetrahydronaphthalene with the Jacobsen catalyst and trans-β-methylstyrene oxide with the Shi catalyst was investigated by computing the energy transition state (TS) structures. The relative energy of the most stable TS geometry for the two enantiomers of a given epoxide is related to the equilibrium constant and was used to determine the enantiomeric excess and the enantiomeric ratio of the products. The NCI and the QTAIM plot for the lowest energy transition state of trans-stilbene oxide with the Shi catalyst was then studied. The stability of the TS was discussed using the information portrayed in those plots.

A brief introduction to molecular mechanics

In order to fully understand the calculations that were be carried in this experiment, the molecular mechanics force field theory that will be used should be explained. The MM2/3/4 theory can be used to obtain the steric energy of a conformer of a molecule. This is called a single point energy computation. The calculation is usually based on five independent energy terms. The bond stretching term (E_bond) is related to the morse portential and represents the energy required to compress and lengthen the bonds in a molecule. The angle bending term (E_θ) is the sum of the energy required to distort the bond angles in the molecule from their ideal geometry. The torsion angle term (E_tor) accounts for the energy related to modifying the dihedral angles between groups in a molecule. Another term reflects the Van der Waal's attraction/repulsion between atom pairs and is related to the Lennard-Jones potential. In ChemBio3D, this term is broken down into short range (E_1,4-VDW) interactions and long range interaction (E_non-1,4-VDW). The latter is defined as the through space interaction between atoms which are separated by more than three atoms.

Computational Analysis Using Molecular Mechanics - Part 1

The Cyclopentadiene Dimer

Figure 1. The dimerisation of cyclopentadiene.

Cyclopentadiene dimerises via a _π4_s + _π2_s cycloaddition to yield either of two isomeric adducts as depicted in Figure 1. This Diels-Alder reaction satisfies the 4n+2 rule for n=1 and is thus thermally allowed via suprafacial components (Hückel topology). Literature states that the endo product of this pericyclic reaction is favoured.

The single point energy of the endo and the exo isomers for the cyclopentadiene dimer was computed on ChemBio3D 14.0 using both MM2 and MMFF94 molecular mechanics calculations. The results are tabulated in Table 1. For exampe, when the endo isomer was optimised using the MMFF94 molecular mechanics level of theory, the adduct reached a minimum energy of 58.1902 kcal/mol. A minimum energy is said to be reached when the gradient of the potential energy curve converges to zero. There is little possibility for conformational rearrangement around the stiff bridgehead olefin product and thus we can assume that the global minimum energy conformation was achieved. Similarly, the optimised exo isomer was calculated to have a minimum steric energy of 55.3731 kcal/mol as the RMS gradient converged to 0.

On ChemBio3D 14.0, the breakdown of the energy terms that contribute to the total steric energy could not be obtained using MMFF94. Thus the relative energy of the endo and exo isomers was computed anew using MM2 and a breakdown of the terms contributing to the total energy was obtained. The ChemBio3D 14.0 user guide also suggests that the MM2 method is more accurate for small molecules containing common atoms such as carbon, hydrogen, nitrogen and oxygen. However, the value obtained for the relative energy of the isomers using the MM2 level of calculation was very similar to that obtained using MMFF94, 2.1211 and 2.8171 kcal/mol respectively.

Table 1. The steric energy endo and exo cyclopentadiene dimers.

	MMFF94		MM2
	Steric Energy (in kcal/mol)	Relative Energy (in kcal/mol)	Steric Energy (in kcal/mol)	Steric Energy Breakdown (in kcal/mol)	Relative Energy (in kcal/mol)
Endo Adduct	58.1902	2.8171	33.9975	Ebond : 1.2509 Eθ : 20.8476 Ebond/θ : - 0.8358 Etor : 9.5109 Enon-1,4-VDW : - 1.5438 E1,4-VDW : 4.3200 Ed/d : 0.4476	2.1211
Exo Adduct	55.3731	0.0000	31.8764	Ebond : 1.2850 Eθ : 20.5805 Ebond/θ : - 0.8380 Etor : 7.6555 Enon-1,4-VDW : - 1.4174 E1,4-VDW : 4.2333 Ed/d : 0.3775	0.0000

The MM2 computed geometric properties were of the highest quality, Q=4, which means that the results are experimentally verified and reliable. The steric energy breakdown generated using the MM2 calculation provided insight into the relative energy of the endo and the exo configurations. The energy term which dominates the relative energy of the isomers is E_tor. The dihedral angles between key groups in both isomers is showed in Table 2. In the endo isomer C¹ and C⁷ are in a gauche configuration whereas there are in an anti-periplanar conformation in the exo dimer. The gauche alignment is higher in energy. The C¹ and C⁷ is also more distorted from an ideal staggered geometry in the endo adduct than the exo adduct. The torsion angle between C² and C⁹ in the endo isomer is also gauche and distorted from the ideal staggered geometry. There is also greater short range VDW repulsive interactions in the endo isomer. This reflects the shorter distance between the atoms shown in Table 2 in the endo than in the exo adduct.

Literature reports that the endo adduct is formed.. The above calculations showed that the exo product has a lower steric energy and is thus more thermodynamically stable. We can conclude from these findings that the reaction is under kinetic control rather than under thermodynamic control. This means that the energy of the endo and exo transition state govern which product is formed rather than the energy of the products. The endo transition state must have a lower energy geometry than the exo transition state and this is why the endo adduct is obtained. This result is supported by the literature.

Table 2. Through space repulsive interactions and torsional strain in the exo and the endo dimers of cyclopentadiene.

Endo-Adduct	Stronger repulsion	Gauche C1-C7 configuration	Gauche C2-C9 configuration
Exo-Adduct	Weaker repulsion	Anti-periplanar C1-C7 configuration	Anti-periplanar C2-C9 configuration

The Hydrogenation of the Cyclopentadiene Dimer

Now, we will investigate the relative energy of the C¹-C² and the C⁸-C⁹ hydrogenated endo adduct. The MM2 level of theory was used to compute the respective steric energy and steric energy terms of the C¹-C² and the C⁸-C⁹ hydrogenated endo dimer. The results are tabulated in Table 3 and show that the C¹-C² hydrogenated molecule is the most stable.

Table 3. The steric energy of the C¹-C² hydrogenated and the C⁸-C⁹ hydrogenated endo adduct.

	MM2
	Steric Energy (in kcal/mol)	Steric Energy Breakdown (in kcal/mol)	Relative Energy (in kcal/mol)	Energy of hydrogenation (ΔE in kcal/mol)
C1-C2 hydrogenated endo Adduct	31.1520	Ebond : 1.0965 Eθ : 14.5244 Ebond/θ : - 0.5494 Etor : 12.4974 Enon-1,4-VDW : - 1.0701 E1,4-VDW : 4.5126 Ed/d : 0.1406	0.0000	-2.8455
C8-C9 hydrogenated endo Adduct	35.9266	Ebond : 1.2348 Eθ : 18.9380 Ebond/θ : -0.7609 Etor : 12.1244 Enon-1,4-VDW : - 1.5018 E1,4-VDW : 5.7290 Ed/d : 0.1631	4.7746	+1.9291

This is mainly due to the angle strain as the E_θ energy term is much bigger in the C⁸-C⁹ hydrogenated cyclopentadiene adduct. Table 4 shows that the bond angles at the sp² carbon center is closer to the ideal 120° angle in the C¹-C² hydrogenated diels-alder adduct than in the other configurational isomer. The E_1,4-VDW energy term also differs significantly for the two hydrogenation product. The short range through space VDW repulsive interactios are stronger in the C⁸-C⁹ hydrogenated compound. This is because C⁸ is at 3.160 Å from both C¹ and C², which is less than twice the VDW radius of carbon (1.70 x 2 = 3.40 Å respectively). In the C¹-C² hydrogenated molecule this distance is greater than two times the VDW radius of carbon, around 3.5 Å, and thus there is no such repulsive interaction. Moreover, there is a greater repulsive Van der Waal's interaction between C¹ & C⁷ and C² & C⁹ in the C⁸-C⁹ than in the C¹-C² hydrogenated endo dimer . To conclude, we can predict that the thermodynamic product of the reaction would be the more stable C¹-C² hydrogenated adduct. Moreover, the electronic energy change for the hydrogenation of C¹ and C² in the endo duels-alder adduct, ΔE_{hydrogenation}, would be exothermic and favourable whereas the formation of the 8,9-hydrogenated adduct is endothermic and requires an energy input.

Table 4. Angle strain in the C¹-C² and the C⁸-C⁹ hydrogenated endo dimers of cyclopentadiene.

C1-C2 hydrogenated cyclopentadiene dimer		C8-C9 hydrogenated cyclopentadiene dimer
Less strained sp2 C7-C8-C9	Less strained sp2 C6-C7-C8	Strained sp2 C5-C1-C2	Strained sp2 C1-C2-C3

Atropisomerism in an Intermediate in the Synthesis of Taxol

Figure 2. The structure of the isomeric bridgehead olefins 1 and 2.

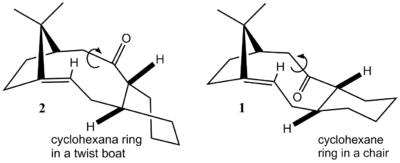
In this section, an intermediate formed during the synthesis of taxol will be studied. The intermediate has two atropisomer, species 1 and 2. An oxy-Cope rearrangement gives rise to those intermediates, which then isomerise to yield a single atropisomer as a stable product. The reaction is therefore atroposelective. Using MM2 molecular mechanics force field calculations, the energy of olefins 1 and 2 can be compared to establish which one of the two is the most stable and hence which atropisomer is found in the final product. The cyclohexane moiety of the bridgehead olefins was drawned in ChemBio3D in a chair conformation for 1 and in a twist-boat conformation for 2 based on literature reports of the structure of the two atropisomers. The optimised molecules maintained this geometry and also had the correct stereochemistry for the three hydrogen atoms showed in Figure 2.

The result of the MM2 energy minimization of the intermediates is shown in Table 5. The relative energy of the isomers is significantly different, with olefin 1 being 97,3180 kca/mol lower in energy. This can be partly explained by the fact that the cyclohexane fragment adopts a twist boat conformation in molecule 2, which has steric, torsional and angle strain. On the opposite, the cyclohexane fragment in 1 is in the stable chair conformation which only suffers from weak 1,3-diaxial repulsive interations. The carbonyl group is in axial position with respect the latter 6-membered rings in both isomers. The C-(C=O)-C angle in 5 is 166.8° as shown in Table 2. This angle is highly strained since the ideal bond angle between substituents at an sp² hybridised center is 120°.

Table 5. The steric energy of bridgehead olefins 1 and 2.

	MM2
C-(C=O)-C Angle Strain	Steric Energy (in kcal/mol)	Steric Energy Breakdown (in kcal/mol)	Relative Energy (in kcal/mol)
Atropisomer 1	42.6828	Ebond : 2.6205 Eθ : 11.3390 Ebond/θ : 0.3432 Etor : 19.6721 Enon-1,4-VDW : - 2.1618 E1,4-VDW : 12.8722 Ed/d : - 2.0023	0.0000
Atropisomer 2	140.0008	Ebond : 7.2792 Eθ : 82.0408 Ebond/θ : - 0.0510 Etor : 20.7044 Enon-1,4-VDW : 1.7446 E1,4-VDW : 31.0828 Ed/d : -2.8000	97.3180

Using the "closed contacts" function on ChemBio3D 14.0, the repulsive interactions between non-bonded atoms was investigated. The program identifies close contacts by comparing the distances between pairs of atoms to the sum of their VDW radius. When the interatomic distance between two non-bonded atoms is less than twice their Van der Waal's radii, the interaction is repulsive (i.e. the r^-12 term of the VDW potential dominates). The Van der Waal's radius of carbon, oxygen and hydrogen are 1.70, 1.52 and 1.2 Å respectively. In atropisomer 2, there are 13 close contacts, 5 of which arise from interactions between the carbonyl oxygen atom and another atom. On the opposite, there are no close contacts involving the carbonyl oxygen in 1 and there are only 7 close contacts. The close contact distances will be quoted as the absolute value of the interatomic distance between the atom pair relative to the sum of the Van der Waal's radius of the atom pair involved (eg. a C-C close contact of 3.00 Å would be equivalent to a relative value of 0.40 Å since the VDW radius of carbon in 1.70 Å and thus the sum of the VDW radius of the atom pair is 3.40 Å).

The only C-H close contact in 1 has a value of 0.3 Å (only 1 decimal place can be used when the hydrogen VDW radius is involved since the data reported by Bondi for VDW radius of H is only precise to one decimal place, 1.2 Å). There is also one C-H repulsive interaction in 2 and the interacting atom pair is almost equidistant to those in close contact in 1. The four H-H close contacts in 1 have values ranging from 0.2 to 0.3 Å. There are three repulsive H-H through space interactions in 2 and they are similar in magnitude those in 1 with an average value of 0.2 Å . The two carbon to carbon close contacts in 1 have a value of 0.59 and 0.50 Å, which means that these close contact distances are significantly lower than the sum of the VDW radii of the interacting atoms. Each of those involve a different one of the two alkene carbons. The two equivalent close contacts in 2 are even closer to one another, at 0.67 and 0.70 Å. There are two further C-C repulsive interactions in 2, which comes from atoms in the twist boat clyclohexane ring. The latter close contacts have a value of 0.60 and 0.62 Å. There are four O-H close contacts in 2 with values ranging from 0.3 to 0.5 Å. There is one C-O repulsive interaction in 2 with a relative close contact value of 0.21 Å. To sum up, the C-C close contact in the twist boat cyclohexane ring in 2 and the five close contacts which involve the carbonyl oxygen cause the repulsive VDW steric energy of atropismoer 2 to be higher than that of 1.

To conclude, atropisomer 2 is less stable then atropisomer 1 due to a higher angle strain and a greater total of VDW repulsive interactions. Thus, it is expected that isomer 2, if formed, will rearrange to give the lower energy isomer 1. Now, we must ask ourselves: are the studied species the lowest energy conformers of species 1 and 2? Unlike the cyclopentadiene dimer, which is rigid, there is a range of stable conformations for species 1 and 2. This will be discussed in the following section.

Further analysis of an intermediate in the synthesis of Taxol

It was initially assumed that the lowest energy conformers of intermediate 1 and 2 respectively had their cyclohexane rings in a chair pointing down and in a twist boat down conformation. Using molecular mechanics, the steric energy of the intermediates will be computed with their cyclohexane ring in four different conformations. The latter include two enantiomeric chair pointing up or down, chair (A) and (B) respectively and two enantiomeric twist-boat pointing up and down, twist boat (A) and (B). Using MM2 to optimise the energy and the geometry of species 1, we obtain that the two chair conformers are of the same energy. When using MMFF94 to optimise the geometry of the molecule, we obtain a single lowest energy conformer. Both methods however agree that a chair down conformation is adopted by the lowest energy conformer of species 1 and this result is in accordance with the literature.

The previously optimised structure for intermediate 2 had the cyclohexane ring a twist-boat conformation, but the carbonyl was in fact pointing to the side and away from the molecule rather than pointing upwards. This caused angle strain and explains why it was so high in energy. It was a local energy minimum rather than a global minimum. The results obtained for the four conformers lowest energy geometry of intermediate 2 using the MM2 molecular mechanics calculations and the MMFF94 method agree. The study of the steric energy of the conformers shows that species 2 is lower in energy when its cyclohexane moiety is in a chair conformation. This suggests that the literature, which described the intermediate's lowest energy conformer as having its cyclohexane ring in a twist-boat conformation, identified a local minima of the potential energy curve and not the global minimum.

Intermediate 1

Conformation	Chair (A)	Twist boat (A)	Chair (B)	Twist boat (B)
Structure
Ebond (in kcal/mol)	2.6205	2.7117	2.6205	2.7042
Eθ (in kcal/mol)	11.3390	11.7419	11.3390	11.8280
Ebond/θ (in kcal/mol)	0.3432	0.3237	0.3432	0.3913
Etor (in kcal/mol)	19.6721	21.8656	19.6721	22.8855
Enon-1,4-VDW (in kcal/mol)	- 2.1618	- 2.0965	- 2.1618	- 1.9931
E1,4-VDW (in kcal/mol)	12.8722	13.9187	12.8722	14.3390
Ed/d (in kcal/mol)	- 2.0023	- 2.0316	- 2.0023	- 1.9973
Etotal (in kcal/mol)	42.6828	46.4335	42.6828	48.1578
Erelative (in kcal/mol)	0.0000	3.7507	0.0000	5.4750
EMMFF94 (in kcal/mol)	60.5499	65.5937	74.7609	66.3100
Erelative (in kcal/mol)	0.0000	5.0438	14.211	5.7601

Intermediate 2

Conformation	Chair (B)	Twist boat (B)	Chair (A)	Twist boat (A)
Structure
Ebond (in kcal/mol)	3.3224	3.0987	2.7831	2.8780
Eθ (in kcal/mol)	20.4884	19.4975	16.5402	17.2772
Ebond/θ (in kcal/mol)	0.4980	0.6078	0.4299	0.4731
Etor (in kcal/mol)	22.0139	23.9752	18.2774	20.6081
Enon-1,4-VDW (in kcal/mol)	- 1.0700	- 0.8007	-1.6035	- 2.1618
E1,4-VDW (in kcal/mol)	14.9656	15.5836	13.1454	14.3741
Ed/d (in kcal/mol)	- 1.8326	- 1.6691	-1.7266	- 1.7086
Etotal (in kcal/mol)	58.3856	60.2931	47.8460	53.0099
Erelative (in kcal/mol)	10.5396	12.4471	0.0000	5.1639
EMMFF94 (in kcal/mol)	82.6200	95.5691	70.5284	88.1254
Erelative (in kcal/mol)	12.0916	25.0407	0.0000	17.5970

A brief note on hyperstable bridgehead olefins

Hydrogenated Species 3

Conformation	Twist-boat (A)
Structure
Ebond (in kcal/mol)	3.1787
Eθ (in kcal/mol)	17.1199
Ebond/θ (in kcal/mol)	0.6107
Etor (in kcal/mol)	23.6950
Enon-1,4-VDW (in kcal/mol)	-0.2141
E1,4-VDW (in kcal/mol)	16.4808
Ed/d (in kcal/mol)	-1.7570
Etotal (in kcal/mol)	59.1138
OS (in kcal/mol)	-12.6803
EMMFF94 (in kcal/mol)	85.9942
OS (in kcal/mol)	-20.4005

The strain originating from the double bond in bridgehead olefins, described in the literature as olefinic strain (OS), is an indactor of the stability of those molecules. In order to investigate the extent of OS in species 1, the hydrogenated derivative of one of the low energy conformers was computed and its energy was compared with that of the corresponding olefin. Species 1 in the twist boat up conformation was chosen. The latter has an energy of 46.4335 kcal/mol based on MM2 calculations and 65.5937 kcal/mol according to MMFF94 computation. The corresponding energy of the hydrogenated molecule is 59.1138 kcal/mol and 85.9942 kcal/mol. Thus, the relative total electronic energy of the hydrogenated compound is 12.6803 kcal/mol and 20.4005 kcal/mol. It is found that the olefin is infact more stable than the hydrogenated derivative. The OS is equal in magnitude but opposite in sign to the relative ΔE_{hydrogenation} and is therefore negative (-12.6803 kcal/mol and -20.4005 kcal/mol). Compound which display this property are called hyperstable bridgehead olefins.

Spectroscopic Simulation using Quantum Mechanics - The Density Functional Theory

In this section, we will optimise and study the steric energy of the respective dithioether derivatives of isomer 1 and 2, which we will call species 3 and 4. The two dithioethers atropisomer are displayed in Figure 3. Species 3 and 4 will be optimised to a minimum using MM2 molecular mechanics calculations. Again, we will test whether the conformers obtained are in fact the lowest energy conformer for species 3 and 4 or whether they are local minima rather than global minima. The ¹H and ¹³C NMR of 3 will be computed using quantum mechanics and will be used to determine whether the true global minimum energy conformation was computed or not. This will be achieved by comparing the computed shifts with the spectroscopic properties reported in the literature for those compounds. Each calculated ¹³C δ will be compared with the ¹³C δ reported in the literature. A difference of more than ± 5 ppm between the experimental and the calculated ¹³C δ for a given carbon would suggest that the conformation around that carbon is not the most stable conformation.

Figure 3. Species 3 and 4

The relative steric energy of a conformer of species 3 and species 4

Species 3 is sketched on ChemBio3D using species 1 as a frameword, that is to say with the cyclohexane ring in a chair conformation, the carbonyl pointing downwards and the double bond in a cis configuration (see the bonds highlighted in pink in Figure 3). The additional 1,3-dithiolane and the methyl substituents were drawn on the molecule to fit the structure reported in the literature. An MM2 energy minimization was then carried out and the cyclohexane ring adopted a twist-boat conformation as the gradient converged to zero. The same steps were followed to generate species 4 from intermediate 2. The geometry obtained is high in energy despite having the cyclohexane moiety in a chair conformation because the sulphur containing heterocycle is very close to the ethyl segment of the bridgehead olefin. This structure is unlikely to be a global minima for species 4. Quantum mechanics could be used to calculate the IR spectrum of species 4. This would allow us to determine whether the gradient converged to zero because the geometry is at a local energy minimum on the potential energy curve or because it is a local maximum. If this optimised structure was a saddle point, the conformation would be a transition state rotamer and would have an imaginary frequency. However, the frequency calculation could not be performed due to lack of time. The structure of the two optimised 1,3-dithiolane substituted species, their individual steric energy and their relative energies is displayed in Table 6.

Table 6. The steric energy of 1,3-dithiolane substituted bridgehead keto-olefins 3 and 4.

	MM2
	Steric Energy (in kcal/mol)	Steric Energy Breakdown (in kcal/mol)	Relative Energy (in kcal/mol)
Species 3	64.2162	Ebond : 4.9572 Eθ : 18.7076 Ebond/θ : 0.7250 Etor : 24.2532 Enon-1,4-VDW : 0.1207 E1,4-VDW : 17.6073 Ed/d : - 2.1548	0.0000
Species 4	152.6659	Ebond : 10.3643 Eθ : 87.2786 Ebond/θ : 0.6876 Etor : 22.7648 Enon-1,4-VDW : 3.3891 E1,4-VDW : 32.2247 Ed/d : -4.0432	88.4497

As before, the species with the carbonyl oxygen pointing down is markedly more stable. However, the quality of the results computed using the molecular mechanics method is poor, Q=1, which means that they are not reliable. The structures are thus re-optimised using density functional theory quantum mechanical calculations (DFT B3LYP/6-31G(d,p)). The free energy obtained for species 3, which has the carbonyl oxygen atom pointing down, is -1651.462784 hartree or -4.335915869 x 10⁶ kJ/mol. Species 4, which has the carbonyl atom pointing up as G = -1651.440534 hartree or -4.335857452 x 10⁶. The relative energy of species 4 with respect to the lowest energy conformer species 3 is 58.42 kJ/mol.

Spectroscopic analysis - The ¹³C and ¹H NMR and the IR spectra of species 3

Quantum mechanics was used to generate the ¹³C and ¹H NMR and the IR spectra of species 3, in order to compare them to the literature. DFT was used with the B3LYP functional and the 6-311+G(2d,p) basis set. The energy and the geometry of the molecules was optimised to a minimum and the keywords "Opt SCRF=(CPCM,Solvent=X) Freq NMR EmpiricalDispersion=GD3" were used. The first option is used to specify the solvent used (X = benzene in this case). The "Freq" and "NMR" keyword specifies that the IR spectrum, the VCD spectrum and the NMR spectrum of the molecules should be computed and the last option is a correction term which accounts for the influence of dispersions forces. The electronic energy obtained for species 3 is -1652.13624419 hartree or -4.33768403955 x 10⁶ kJ/mol and its free energy is calculated to be G = -1651.718580 hartree = -4.33658746213 x 10⁶ kJ/mol.

Figure 4. The computed IR of Species 3 using the DFT B3LYP/6-311+G(2d,p) level of theory

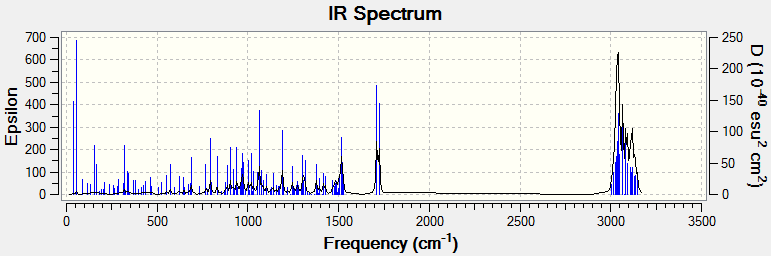
No imaginary frequencies were found in the infrared spectrum of species 3 after optimisation which suggest that the optimised species is a true conformer of the bridgehead olefin species and not a transition state conformation DOI:10042/160410 . The synchronous and asynchronous C=C and C=O are found at 1710 cm^-1 and 1724 cm^-1 respectively. The C(sp²)-H and C(sp³~)-H stretches appear in the 3005-3146 cm^-1 range with the C(sp²)-H stretches being higher in energy as expected. The C-H in-plane (ip) bends are found at higher energies than the out-of-plane (oop) bends. C-H scissoring (ip) gives rise to the peaks observed at 1519 cm^-1 and 1514 cm^-1. The peaks at 1063 cm^-1 and 1189 cm^-1 are caused by C-H rocking motion (ip). The C-H oop bends are observed at 1303 cm^-1, 1315 cm^-1, 1376 cm^-1 and 1417 cm^-1. The first two correspond to C-H twisting motion and the latter two are caused by C-H wagging.

Table 7. The calculated ¹³C NMR shift of species 3 and the reported literature values (in C₆D₆).

Computed values DFT B3LYP/6-311+G(2d,p)		Literature values	Difference between computed and literature values
13C NMR spectrum assignment and comparison with the literature	δ (in ppm)	δ (in ppm)	Spread (in ppm)
Figure 5. The computed 13C NMR of Species 3 in benzene using the DFT B3LYP/6-311+G(2d,p) level of theory and the difference between the computed and the literature values	224.62 C=O	211.49	-13.13
	159.82 C=C	148.72	-11.10
	126.52 C=C	120.90	-5.62
	91.80 S-C-S	74.61	-17.19
	70.21	60.53	-9.68
	58.40	51.30	-7.10
	57.58	50.44	-7.14
	52.07	45.53	-6.54
	49.91	43.28	-6.63
	47.74	40.82	-6.92
	41.97	38.73	-3.24
	39.07	36.78	-2.29
	36.97	35.47	-1.50
	32.41	30.84	-1.57
	28.76	30.00	1.24
	28.53	25.56	-2.97
	26.01	25.35	-0.66
	24.46	22.21	-2.25
	22.29	21.39	-0.90
	21.15	19.83	-1.32

Table 8. The calculated ¹H NMR shift of species 3 and the reported literature values (in C₆D₆).

Computed values DFT B3LYP/6-311+G(2d,p)		Literature values	Difference between computed and literature values
13C NMR spectrum assignment and comparison with the literature	δ (in ppm)	δ (in ppm)	Spread (in ppm)
Figure 5. The computed 1H NMR of Species 3 in benzene using the DFT B3LYP/6-311+G(2d,p) level of theory and the difference between the computed and the literature values	5.19	5.21 (m, 1H)	0.002
	3.44	3.00-2.70 (m, 6H)	-0.44
	3.25		-
	3.17		-
	2.99		-
	2.77		-
	2.56		0.14
	2.46	2.70-2.35 (m, 4H)	0.24
	2.32		-
	2.20		-
	2.05		0.30
	2.01	2.20-1.70 (m, 6H)	0.19
	1.94		-
	1.93		-
	1.85		-
	1.76		-
	1.75		-0.05
	1.71	1.58 (t, 1H)	-0.13
	1.56	1.50-1.20 (m, 3H)	-0.13
	1.36		-
	0.95		0.25
	1.34 (3H, s)	1.10 (s, 3H)	-0.24
	1.16 (3H, s)	1.07 (s, 3H)	-0.09
	1.08 (3H, s)	1.03 (s, 3H)	-0.05

The computed ¹³C NMR for species 3 along with the chemical shift reported in the literature are showed in Table 7. The difference between the computed and the experimental values is represented graphically and tabulated in Table 7. There is a major difference between the computed ¹³C NMR shift obtained for C₄ and the literature value. This is because spin orbit coupling between C₄ and and the two adjacent "heavy" sulphur atoms leads to errors in the computed value. The same effect explains the discrepancy between the calculated and the experimental chemical shift for C₉ and C₁₀ and for H₂ in the ¹H NMR spectrum. The magnitude of the error is smaller for C₉ and C₁₀ than for C₄ as the former are only have one neighbouring sulphur atom. The computed chemical shift for the carbonyl carbon is also significantly different to the value reported in the literature. This can be explained partly by spin-orbit coupling related error in the computation. It might also indicate that the carbonyl is in the wrong conformation and thus that the neighbouring cyclohexane ring is not in the lowest energy conformation. The difference between the literature values and the computed values for C₁, C₂, C₅, C₆, C₇ and C₈ is bigger than ± 5 ppm. It is hypothesized that this is because the conformation around those carbon atoms is not in the ground state. This could also explain why the energy of the concerted C=O and C=C stretches in the IR spectrum of species 3 is higher that the ones reported in the literature (1710 cm^-1 and 1724 cm^-1 vs. 1675 cm^-1 and 1470 cm^-1). The majority of the proton chemical shifts that deviate significantly from the literature values involve atoms in the cyclohexane ring. Again, this suggests that the lowest energy conformer should not have the cyclohexane ring in a twist-boat conformation.

To conclude, we have successfully used molecular mechanics and quantum mechanics to optimised the geometry of a conformer of species 3. ¹³C NMR and ¹H NMR were successfully used to show that a local minimum rather then a global minimum was identified. It would have been interesting to compute the IR spectrum of the conformer obtained for species 4 using DFT frequency calculation to find out whether a transition state rotamer was indeed computed!

Further analysis of the dithioether derivative of an intermediate in the synthesis of Taxol

In order to further confirm that the conformer of species 3 that was computed is indeed a local minimum, the energy of the four lowest energy conformation of the compound will be computed on ChemBio 3D using MMFF94 molecular mechanics calculations. MMFF94 is used rather than MM2 because the ChemBio 3D user guide suggest that the former force field theory is more adequate to establish the relative energies of molecules containing atoms other than oxygen, nitrogen, carbon and hydrogen. Species 3 has two sulphur atoms. The results are tabulated below. We found that the structure that we had been using so far had the twist-boat down conformation, twist-boat (B) rather than the lower energy chair up conformation, chair (A). In this exercise, NMR analysis and conformational studies allowed to determine that the lowest energy conformer of species 3 had not been successfully computed.

Intermediate 1

Conformation	chair (A)	twist boat (A)	chair (B)	twist boat (B)
Structure
EMMFF94 (in kcal/mol)	96.981	102.213	100.428	102.302
Erelative (in kcal/mol)	0.0000	5.232	3.447	5.321

Analysis of the products of the asymmetric expoxidation of alkenes - Part 2

The Shi and the Jacobsen Catalysts

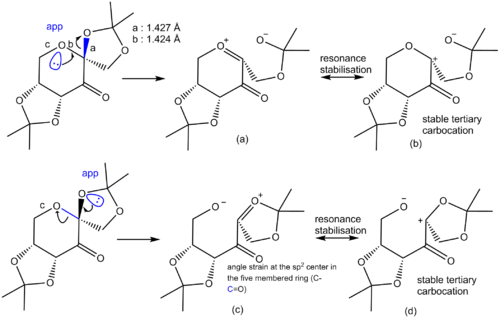
In 1996, Shi and co-workers successfully prepared a catalyst for the asymmetric epoxidation of trans-alkenes and tri-substituted olefins. The fructose based catalyst is showed below. Analysis of the C-O bond length at the anomeric centre is interesting. The structure of the diketal Shi catalyst (CID=7275400) was obtained from the PubChem Compound Database of the National Center for Biotechnology Information. The carbon-oxygen bond with the oxygen in the 6-membered ring as a length of 1.424 Å. The C-O bond to the oxygen in the 5-membered axial substituent is slightly longer at 1.427 Å. Both C-O bonds at the anomeric center are slightly longer than the sum of the covalent radii of C and O. The covalent radius oxygen and carbon are 0.661 Å and 0.762 Å respectively for a total bond lenght of 1.423 Å. The axial C-O bond is however shorter than the other axial C-O bond in the molecule on the 6-membered heterocycle (e.g. 1.432 Å). The anomeric C-O bond on the the tetrahydropyran moiety is also shorter than the other C-O bond on the tetrahydropyran ring. It is thus relevant to ask ourselves Why are the C-O bond at the anomeric center shorter. The figure below shows the resonance form at the anomeric center. Bothn C-O bonds are closer in length to a single bond because of the high contribution of the resonance form with the stable tertiary carbocation. The latter also avoids having positive charge on an electronegative oxygen atom. The axial C-O bond is longer because resonance form (c) is less stable than (a). This could be because sp² center suffer from angle strain in 5-membered rings, which would increase the steric energy of the (c) vs. (a).

Figure 6. Resonance forms at the anomeric center of the Shi Catalyst

Five years earlier, in 1991, Eric Jacobsen and his colleagues also devised a catalyst for the asymmetric epoxidation of alkenes. The Mn(III) salen compound that was discovered by Jacobsen and his co-workers showed good enantioselectivity for cis-alkenes. The crystal structure of the catalyst was found and analysed using Conquest and Mercury (Structure CCDC ref. number: 804841). The manganese center is square based pyramidal. The Van Der Waal's radius of t-Bu is 3.00 Å yet the distance between adjacent tert-butyl groups on the same phenyl ring is between 5.09-5.08 Å and the distance between the closest t-Bu groups of the two rings is 5.46 Å. Therefore, the side of the Mn^III(Salen) complex with the t-bu substituted phenyl rings is very sterically crowded. This makes it hard to bind and epoxidise trans-substrates whereas it can easily do so with cis-alkenes.

Shi catalyst

Jacobsen catalyst

Chiroptical properties of the epoxides of trans-β-methylstyrene and 1,2-dihydronaphthalene

Optical rotation (OR) data was gathered for the two enantiomers of trans-β-methylstyrene oxide and 1,2-epoxy-1,2,3,4-tetrahydronaphthalene. The data was generated using the density functional theory, the CAM-B3LYP functional and the 6-311⁺⁺G(2df,p) basis set. The CAM derivative of the B3LYP functional method is used because it yields more accurate optical rotation values. The solvent used for the calculation was chloroform and the incident wavelength is set to the sodium D line, 589 nm. The OR values optained for (S,S)-trans-β-methylstyrene oxide, (R,R)-trans-β-methylstyrene oxide, (1R,2S)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene and (1S,2R)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene respectively were [α]_D= -248.74° (DOI:10042/158048 ), [α]_D= +248.74° (DOI:10042/161018 ), [α]_D= +222.95° (DOI:10042/161019 ) and [α]_D= -222.95° (DOI:10042/158054 ). These results differed a lot from the values reported in the literature for those compound therefore the optimisation was carried out anew. This time however, the structure were pre-optimised using the MMFF94 rather than the MM2 molecular mechanics method on ChemBio 3D. The new values obtained were a better match for the literature. This is because MM2 is not appropriate for molecules containing sulphur atoms. MMFF94 is better in those cases. Those results are tabulated below:

Optical rotation of the epoxides of trans-β-methylstyrene and 1,2-dihydronaphthalene and literature OR and ee.

Epoxide	trans-β-methylstyrene oxide		1,2-epoxy-1,2,3,4-tetrahydronaphthalene
	(S,S)	(R,R)	(1R,2S)	(1S,2R)
Structure
Calc. [α]D (in CDCl3)	-103.25°	+103.25°	-183.05°	+183.05°
DOI to log files for the Calc. [α]D	DOI:10042/161085	DOI:10042/161087	DOI:10042/161086	DOI:10042/161088
Lit. [α]D (in CDCl3)	-46.9°	+45.3°, +47.8°	-133°, -144.90°	+133°
Lit. ee %	95.6	91-92, 95.5	99.8, 98	98

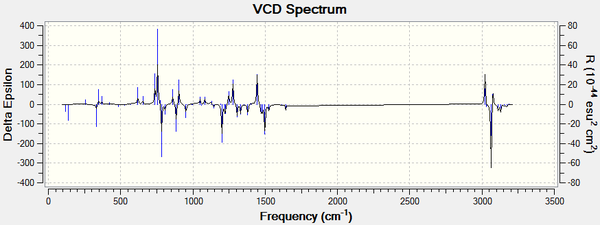
For all enantiomers, the sign of the optical rotation computed agrees with the literature. The magnitude of the OR values computed, however, is higher than the experimental results reported in the literature. For example, the optical rotation value reported in the literature for (1R,2S)-(-)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene by the Sasaki group is -144.90° (c = 0.33, CHCl₃) and the computed value is -183.05°. If we assumed that the computed optical rotation for this epoxide is correct, than the ee reported in the literature is inaccurate. Using the value computed, the optical purity of the product sample reported in the literature would be 79 % rather than 98 %. The remaining 21 % is an optically inactive 1:1 racemic mixture of the (1R,2S) and the (1S,2R) eneantiomes. Therefore, the er would be 90 : 10. It is noted that the literature agrees for a value around 140°., , . The computed value showed to vary greatly depending on the molecular mechanics method used to pre-optimise the epoxides and thus it is more likely that the computed results are inaccurate. Moreover, trans-β-methylstyrene oxide has an optical rotation of less than ± 50° and thus this measurement alone cannot be used to assign its absolute conformation with certitude. Further analysis of the epoxides is needed to assign their configuration with certainty. Generating the electronic circular dichroism (ECD) spectra of the four epoxides under investigation would not be helpful to assign their stereochemistry as they are not chromophores. A vibrational circular dichroism (VCD) spectrum was however generated for the oxygenated compounds at the DFT B3LYP/6-311+G(2d,p) level of theory. The CAM-B3LYP method and the 6-311⁺⁺G(2df,p) basis set are not needed here to obtain good results. This would confirm the absolute configuration assignments if they could be compared with the literature but unfortunately the VCD of the epoxides was not found in the literature. We can however observe that the plot of the each enantiomeric pair of epoxides are mirror images of one another.

(1R,2S)-(-)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene	(1S,2R)-(+)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene
(R,R)-(+)-trans-β-methylstyrene oxide	(S,S)-(-)-trans-β-methylstyrene oxide

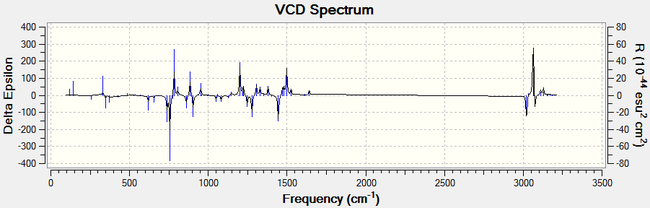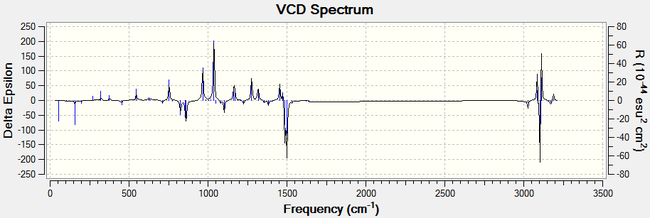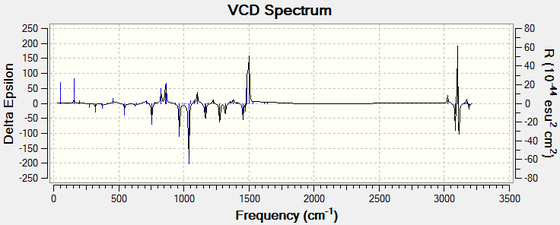A comparison of the computed ¹H and ¹³C NMR spectra for trans-β-methylstyrene oxide and 1,2-epoxy-1,2,3,4-tetrahydronaphthalene with the literature

The ¹H NMR and the ¹³C NMR of trans-β-methylstyrene oxide was computed as carried out previously for intermediate 1 at the DFT B3LYP/6-311+G(2d,p) level of theory and with TMS as a standard DOI:10042/161069 . Both structure were pre-optimised using MMFF94 molecular mechanics calculations on ChemBio 3D. The ¹H NMR spectra in chloroform for 1,2-epoxy-1,2,3,4-tetrahydronaphthalene was computed at the DFT B3LYP/6-311+G(2d,p) level of theory and TMS was used as a standard DOI:10042/161068 . The results were in accordance with the literature as shown in the table below. For both epoxides, the phenyl hydrogens chemical shifts seem to diverge most from the experimental values.

Table 8. The calculated ¹H NMR shift of trans-β-methylstyrene and the reported literature values (in CDCl₃).

Computed values DFT B3LYP/6-311+G(2d,p)		Literature values	Difference between computed and literature values
1H NMR spectrum assignment and comparison with the literature	δ (in ppm)	δ (in ppm)	Spread (in ppm)
Figure 6. The computed 1H NMR of the epoxide and the difference between the computed and the literature values	7.70	7.20-7.40 (m,5 H)	- 0.30
	7.65		-
	7.60		-
	7.57		-
	7.42		- 0.22
	3.55	3.57 (d,1 H)	0.02
	2.87	3.03 (qd, 1H)	0.16
	1.34 (3H, average δ of methyl protons)	1.45 (d,3H)	0.11

Table 9. The calculated ¹³C NMR shift of trans-β-methylstyrene and the reported literature values (in CDCl₃).

Computed values DFT B3LYP/6-311+G(2d,p)		Literature values	Difference between computed and literature values
13C NMR spectrum assignment and comparison with the literature	δ (in ppm)	δ (in ppm)	Spread (in ppm)
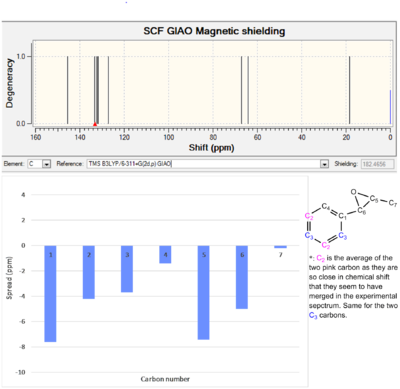Figure 7. The computed 13C NMR of the epoxide and the difference between the computed and the literature values	145.5	137.9	-7.6
	132.8	128.6	-4.2
	131.9	128.2	-3.7
	127.1	125.7	-1.4
	67.1	59.7	-7.4
	64.2	59.2	-5.0
	18.3	18.1	-0.2

Table 10. The calculated ¹H NMR shift of 1,2-epoxy-1,2,3,4-tetrahydronaphthalene and the reported literature values (in CDCl₃).

Computed values DFT B3LYP/6-311+G(2d,p)		Literature values	Difference between computed and literature values
1H NMR spectrum assignment and comparison with the literature	δ (in ppm)	δ (in ppm)	Spread (in ppm)
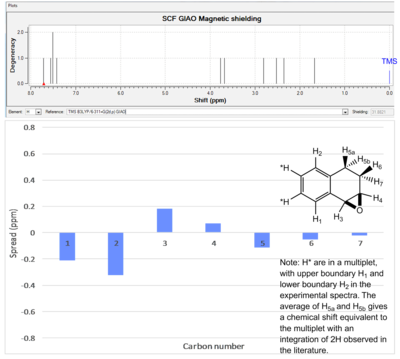Figure 8. The computed 1H NMR of the epoxide and the difference between the computed and the literature values	7.71	7.1-7.5 (m, 4H)	- 0.21
	7.55		-
	7.51		-
	7.42		- 0.32
	3.77	3.95 (d,1H)	0.18
	3.68	3.75 (dt,1H)	0.07
	2.67 (2H, average δ of 5a and 5b)	2.55 (m,2H)	-0.12
	2.35	1.65-2.3 (m,2H)	-0.05
	1.63		-0.02

Table 11. The calculated ¹³C NMR shift of 1,2-epoxy-1,2,3,4-tetrahydronaphthalene and the reported literature values (in CDCl₃).

Computed values DFT B3LYP/6-311+G(2d,p)		Literature values	Difference between computed and literature values
13C NMR spectrum assignment and comparison with the literature	δ (in ppm)	δ (in ppm)	Spread (in ppm)
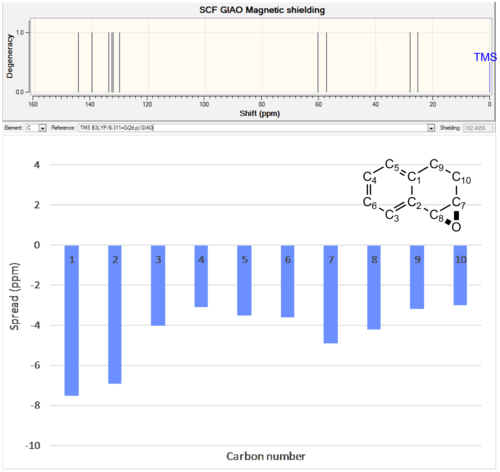Figure 9. The computed 13C NMR of the epoxide and the difference between the computed and the literature values	144.6	137.1	-7.5
	139.8	132.9	-6.9
	133.9	129.9	-4.0
	132.9	129.8	-3.1
	132.3	128.8	-3.5
	130.1	126.5	-3.6
	60.4	55.5	-4.9
	57.4	53.2	-4.2
	28.0	24.8	-3.2
	25.2	22.2	-3

The Shi Catalysed epoxidation of trans-β-methylstyrene - An analysis of the enantioselectivity of the catalyst

Pre-computed transition state structures (TS) at the DFT RwB97XD/6-311G(d,p) level of theory for the Shi catalysed epoxidation of trans-β-methylstyrene were used to study the relative energies of the different transition states. A single enantiomer of the Shi catalyst is used and there are thus eight possible TS. Their energies is tabulated below. The RMS gradient is showed to converge to zero for all structures which highlights the fact that they are local maxima of the potential energy curve (saddle points on the potential energy surface). The energy of the most stable TS with (R,R)- and (S,S)-trans-β-methylstyrene, R,R(4) and S,S(4), were used to calculate the equilibrium constant K using the formula ΔG = -RTln(K). The calculated K-value for R,R(4) ⇌ S,S(4) is : 5.6945 x 10^-2. This means that the equilibrium lies to the left (i.e. towards the most stable TS geometry, R,R(4)). The enantiomeric ratio (er, in %) is thus 94.61 : 5.39 R,R(4) : S,S(4) and the ee % is 89.22 %. The literature reports this values to vary between 88 % in favour of the (+)-R,R enantiomer for 100% conversion of the alkene starting material and at room temperature. The value varies depending on the solvent used.

The energy of the transition state of the Shi catalysed epoxidation of trans-β-methylstyrene

Properties	R,R(1)	R,R(2)	R,R(3)	R,R(4)	S,S(1)	S,S(2)	S,S(3)	S,S(4)
Gradient	0.00000246	0.00000217	0.00000196	0.00000183	0.00000642	0.00000203	0.00000280	0.00000118
Free energy, G (in hartree)	-1343.022970	-1343.019233	-1343.029272	-1343.032443	-1343.017942	-1343.015603	-1343.023766	-1343.024742
Free energy, G (in kcal/mol)	-842759.8175	-842757.4725	-842763.7720	-842765.7619	-842756.6624	-842755.1946	-842760.3170	-842760.9294
Relative Free energy (in kcal/mol)	5.9444	8.2894	1.9899	0.0000	9.0995	10.5673	5.4479	4.8325

The Jacobsen Catalysed epoxidation of 1,2-dihydronaphthalene - An analysis of the enantioselectivity of the catalyst

Once again, the energy and the geometry of pre-optimised transition states at the DFT RwB97XD/6-311G(d,p) level of theory are used to determine the relative energy of the four possible TS geometry for the Mn(III)salen catalyst. One enantiomer of the catalyst is used for all TS structure. The most stable TS geometries for the formation of (1R,2S)- and (1S,2R)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene are 1R,2S(1) and 1S,2R(3). The equilibrium constant K for the following equilibrium, 1R,2S(1) ⇌ 1S,2R(3), is calculated to be 2.925 x 10^-2. The er (in %) is thus 97.158 : 2.842 and the ee is 94.316 % in favour of (1R,2S)-1,2-epoxy-1,2,3,4-tetrahydronaphthalene. The literature reports the ee % for the catalyst with the opposite stereochemistry to the one used in the computation ((S,S) rather than (R,R)). The literature thus reports an ee of 86 % in favour of the (1S,2R)-epoxide. This makes sense as the geometry of the catalyst is inverted and thus the epoxide forms on the opposite face of the catalyst , However, the magnitude of the ee should not be affected. Indeed, the computed and the literature values are similar in magnitude.

The energy of the transition state of the Jacobsen catalysed epoxidation of 1,2-dihydronaphthalene

Properties	R,S(1)	R,S(2)	S,R(1)	S,R(2)
Gradient	0.00000139	0.00000248	0.00000347	0.00000275
Free energy, G (in hartree)	-3421.369033	-3421.361580	-3421.359354	-3421.359499
Free energy, G (in kcal/mol)	-2146941.941	-2146937.264	-2146935.867	-2146935.958
Relative Free energy (in kcal/mol)	0.000	4.677	6.074	5.956

Non-Covalent-Interaction (NCI) analysis of the Transition State of the Shi Catalysed Epoxidation of (R,R)-Trans-Stilbene

Non-covalent interaction (NCI) analysis allows us to visualize the through space interaction between non-covalently bonded atoms. They include Van der Waal's forces and hydrogen bonding. The interaction can be strongly repulsive (red), moderately repulsive (yellow), weakly attractive (green) or strongly attractive (blue). The lowest energy transition state geometry for the chosen enantiomer of the Shi catalyst and the trans-stilbene substrate is shown in Figure 9. The NCI plot shows a lot of attractive interaction and justifies the stability of the TS. When this TS structure breaks down into products, it leads to the formations of (R,R)-trans-stilbene. (R,R)-trans-stilbene is thus the kinetically favoured enantiomer. The two C-O covalent bonds in the process of being formed cause the blue-ish ring seen above the double bond. The only repulsive interaction noted in the TS are intramolecular. The were most likely present in the free catalyst and substrate and thus do not destabilised the transition state. Three intermolecular hydrogen bonding interactions are noted in the TS and four intramolecular hydrogen bonding interaction are observed within the catalyst moiety. Four favourable interaction between a -C-H in the catalyst and -C-H in the substrate are noted. The same quantity of those dipole-dipole interactions is noted within the catalyst itself.

Figure 9: NCI analysis of the lowest energy transition state for Trans-Stilbene

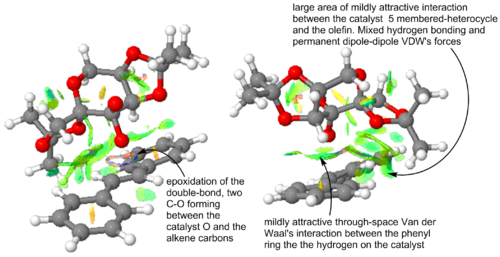Electronic topology - QTAIM analysis of the Transition State of the Shi Catalysed Epoxidation of (R,R)-Trans-Stilbene

The NCI analysis allowed to visualise the curvature and the degree of attractiveness/repulsiveness of non-covalent through space interactions. QTAIM analysis allows to observe the points where the first derivative of the electron density, calculated with respect to x,y and z coordinates coordinates, is zero between a pair of atoms. Those points are shown as yellow spheres in Figure 10 and are called bond critical points (BCP). This techniques illustrates the number of favourable interactions between the catalyst and its substrate better but it does not illustrate the degree of attractiveness of the through space interaction in the TS and does not portray repulsive interactions at all. In the structure under investigation, there is no substrate-catalyst repulsive interaction and thus this is not a major disadvantage. Nevertheless, in other systems, those interaction may be key to the relative stability of the different TS geometries. Thus, the QTAIM and the NCI plot are complementary.

Figure 10. The QTAIM wireframe plot of the transition state of the Shi catalysed epoxidation of (R,R)-trans-stilbene

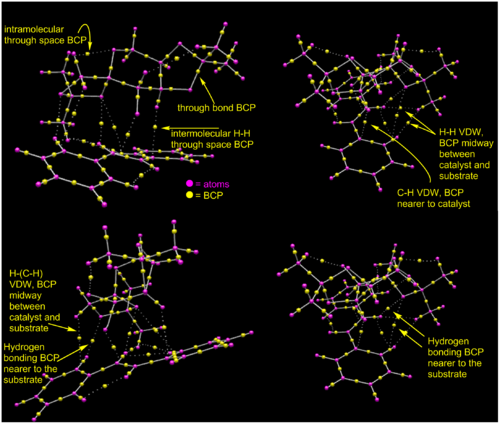
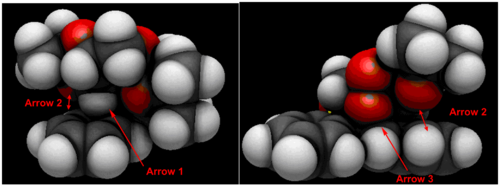
From Figure 10 we can see that there is in fact three hydrogen bonding interactions between the olefin moiety and the diketal catalyst. There are four hydrogen-hydrogen and one C-H Van Der Waal's interactions between to two molecules. Visualisation of the Van der Waal's atomic orbital shows that the AO of the hydrogen in the latter C-H interaction is in fact almost at the center of the phenyl ring of the stilbene substrate below and is potentially interacting with the delocalised system of π electrons in the ring rather than to the closest carbon. This hydrogen in question is shown by Arrow 1. The oxygen of the catalyst and the hydrogen atom of the substrate pointed by double-arrow 2 looked to be hydrogen bonded in the NCI plot and are in fact are not interacting according to the QTAIM plot. The AO of the oxygen atom in the process of reacting with the olefin in shown by arrow 3 is overlapping with the C=C atoms AO.

Figure 10. The Van der Waal's AO plot of the transition state of the Shi catalysed epoxidation of (R,R)-trans-stilbene

Possibility for further study

The epoxidation of 2-methylnaphthalene-1,4-dione (IUPAC name) has been reported. The common name of the starting material is Vitamin K3 and the olefin is available at Sigma-Aldrich as a crystalline yellow solid. The optical rotation of the (2S,3R)-enantiomer of the 2,3-epoxy-2-methylnaphthalene-1,4-dione species is reported to have an optical rotation of +356° for an ee of 34%. This means that the optical rotation of the pure compound must be around 1047°. The epoxide could be optimised as before using the density functional theory. We could confirm that the correct species as been optimised by comparing the NMR spectra of the epoxide with the literature. For example, a big difference between the computed chemical shift of a carbon atom in the optimised molecule and the experimental chemical shift would indicate that this carbon is probably in the wrong conformation. After the correct structure has been computed, the optical rotation and the VCD spectrum could be used to determine the absolute configuration of the molecule and compared with the literature. Using transition state analysis, the ee of the reaction could be calculated and compared with the literature. It would be interesting to see whether the TS analysis shows that the favours enantiomer is in fact the opposite of the one reported in the literature or if the literature reports are correct.

Figure 11. The synthesis of an epoxide