Rep:Mod:EG92

Physical Module: Transition states and Reactivity

The Cope Rearrangement

Optimizing the Reactants and Products

In Gaussview, 1,5-hexadiene was drawn (it can be seen here), the middle 4 carbons are in an anti periplanar conformation. The structure was cleaned up and the structure was optimised using the Hartree-Fock/3-21G basis set.

The process was repeated with several other conformations of 1,5-hexadiene, the results are summarised in the table below with the total energies and point groups.

Anti

Total energy = -231.69402232 a.u. Symmetry C1 This corresponds to anti 4 conformation.

Gauche

Total energy = -231.68916017 Symmetry C1 This corresponds to gauche6 conformation.

The energies are stated in a.u. they are in Hartrees, the atomic unit of energy, 1 Ha = 1.36 E^-18 J.

The energy of anti 2 shown above is -231.69254 a.u. Comparison of this value with that already provided values shows that they are close agreement and so the correct conformation has been drawn and total energy calculation found.

This molecule was reoptimised using a slightly larger basis set, at the B3LYP/6-31G* level. The total energy calculated =-234.61170281 a.u. with C_i symmetry. Qualitatively the geometries look very similar and they both have the same point group. On closer inspection, the bond lengths and bond angles are slightly different to each other.

IR spectrum of anti 2 using B3LYP basis set

A frequency calculation was carried out to find the energy of the molecule on the potential energy surface. This was done twice at the HF/3-21G and then B3LYP/6-31G(d)level. The frequency calculation includes some correctional terms which then allow the energies to be compared with experimental values. This frequency calculation was also used to check that all the vibrational frequencies were real and positive, and hence the critical point, or minimum was found.

1. The sum of electronic and zero-point energies is the potential energy at 0 K including the zero-point energy, E = E_elec + ZPE.
2. The sum of electronic and thermal energies is the energy at 2.98.15 K, with a pressure of 1 atm. At this temperature, translational, rotational, vibrational and electronic contributions are included, E = E_elec + E_trans + E_rot + E_vib.
3. The sum of electronic and thermal enthalpies has an extra enthalpy term for RT, this is considered when looking at dissociation reactions, H = E + RT.
4. The sum of electronic and thermal free energies has a term to include the entropic contribution to the total energy.

Summary of energies with HF/3-21G basis set

Sum of electronic and zero-point Energies=           -231.539540
Sum of electronic and thermal Energies=              -231.532567
Sum of electronic and thermal Enthalpies=            -231.531623
Sum of electronic and thermal Free Energies=         -231.570913

Summary of energies with B3LYP/G-31(d) basis set

Sum of electronic and zero-point Energies=           -234.469205
Sum of electronic and thermal Energies=              -234.461858
Sum of electronic and thermal Enthalpies=            -234.460913
Sum of electronic and thermal Free Energies=         -234.500783

Summary of energies in Ha

	HF/3-21G			B3LYP/6-31G(d)
	Electronic energy	Sum of electronic and zero-point Energies at 0 K	Sum of electronic and thermal energies at 298.15 K	Electronic energy	Sum of electronic and zero-point Energies at 0 K	Sum of electronic and thermal energies at 298.15 K
Calculated	-231.69253530	-231.539540	-231.532567	-234.61170281	-234.469205	-234.461858
Experimental.	-231.692535	-231.539539	-231.532566	-234.611710	-234.469203	-234.461856

These contributions were recalculated at the B3LYP/6-31G(d) at 0 K. The calculation does not run at 0 K, so it was re-run at 0.0001 K using the keyword temperature=0.0001. The following energies were obtained:

Sum of electronic and zero-point Energies=           -234.469212
Sum of electronic and thermal Energies=              -234.469212
Sum of electronic and thermal Enthalpies=            -234.469212
Sum of electronic and thermal Free Energies=         -234.469212

At 0K, you expect to only have zero-point energy, the translation, rotational and vibrational energies do not contribute to the total energy. Therefore you expect that all the energies calculated will be equal to the zero-point energy which can be seen in the table above.

Optimizing the "Chair" and "Boat" Transition Structures

An allyl fragment was drawn (CH₂CH₂CH₂) and the structure was optimised using the HF/3-21G basis set. The fragment was copied and the second fragment was aligned above the first one so it looks like the chair transition state as shown in the Physical Module 3

Method 1 - Hartree Fock/3-21G

This guess transition structure was optimised and the frequency was calculated with Hartree fock and 3-21G basis set. This is the default basis set for most caluclations. This was done using 'Opt+Freq' as the job type, and optimised to a 'TS(Berny)', the force constants were calculated once with Opt=NoEigen which stops the calculation crashing if more than one imaginary frequency has been calculated. This is done as for this calculation as we only want one imaginary frequency, we want the rest of frequencies to be real and positive. Imaginary frequencies can occur if the guess transition state is not close enough. One imaginary frequency was calculated at -818cm^-1. This frequency has been animated and is shown below, this frequency is the vibration associated with the Cope rearrangement.

This method is used when a close guess to the transition state can be made, the Hessian can be calculated (the force constant matrix) initially and then it can be updated as the optimisation occurs. This method can sometimes is expensive (take a long time) and so other methods may be quicker and easier (cheaper) such as the method carried out below.

Method 2 - Frozen coordinate method

The chair transition state was then optimised using a different method, the frozen coordinate method. The main atoms involved in the reactions (the atoms that bonds are formed or broken between) can be frozen while the rest of the structure is minimised. The frozen bond lengths can then be removed and the structure can be optimised again. This method works well when a good guess of the transition state cannot be made.

This was done by drawing a guess structure for the chair tranisition state as done above, using the Redundant Coord Editor the terminal carbons were frozen to a bond distance of 2.2Å. This distance is used as it is longer than a bond but shorter than the sum of 2 Van Der Waals radii and so the bond length is a reasonable guess for the distance in the transition state. The structure was optimised to a minimum, ensuring that 'Opt=ModRedundant' is part of the input line.

The checkpoint of the optimised structure was opened and the structure looked the same as the optimised structure for the method used above. The terminal carbon bond distances were 2.2Å, these were optimised by selecting the 'derivative' option instead of freezing the coordinates. The transition state was optimised, without any force constants being calculated.

A labelled image of the optimised transition state can be seen here.

Bond lengths Å

Bond	Method 1	Method 2
C1-C14	2.02073	2.02091
C6-C9	2.01842	2.02088

Comparison of the bond lengths shows that both methods optimise the structure almost identically. The bond lengths are all within 0.002 Å of each other. The size of the system that has been analysed is small enough that there is not much difference with the levels of theories used.

Optimisation of the boat transition state - QST2

The boat transition state was optimised using another method, the QST2 method. Here that reactants and products are drawn the Gaussian will find the structure in between the reactants and products to find the transition state.

The optimised anti 2 1,5-hexadiene was used as the reactant molecule. The product molecule was pasted into a second window and the atom were labelled. The labelled reactant and product can be seen.

The calculation was optimised to a transition state 'TS(QST2)', the frequency was also calculated. The following transition state was generated:

The job should fail. The calculation ran, but it optimised it to the chair transition structure, not the boat that we want. To do this we need to move the molecule so it resembles the boat transition structure more closely.

The geometries of the reactant product was edited so it looks more like the boat transition state, the labelled reactant and product can be seen. The calculation was re-run and the following was obtained:

Boat TS

TS	Animation -840cm-1

The animation shows that the Cope reaction is asynchronous.

IRC

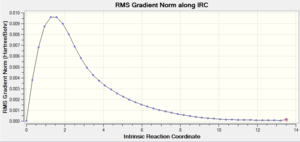
It is not possible to infer from the optimised structure which conformer it will lead to the formation of. Using the Intrinsic Reaction Coordinate (IRC) method within Gaussian, the final structure can be determined. The IRC follows the minimum energy pathway on the potential energy surface to the formation of the product structure.

To do this, the checkpoint file for the optimised structure from method 2 was used. The reaction is symmetrical and so when calculating the IRC, the reaction coordinate is calculated in the forwards direction only, and the force constants were calculated always. The default number of points calculated along the IRC is 10, but this was changed to 50.

IRC total energy

RMS IRC

Chair TS IRC

IRC	Animation

The structure was minimised in 44 steps, the energy for the optimised structure is -231.6957888 a.u. which corresponds to the gauche 2 conformation.

The same process was repeated for the boat transition structure. The following was calculated:

IRC total energy

IRC total energy

Boat TS IRC

IRC	Animation

The structure was minimised in 45 steps and this corresponds to gauche 3 conformation

Activation energy

The activation energy was calculated by reoptimising the reactants and the chair and boat transition structures with the B3LYP/6-31G(d)basis set. Frequency calculations were run on the chair and boat transition structures and the difference in energy between the reactants and transition structure was compared and then multipled by 627.509 to convert the energy from Hartrees to kcal/mol. The activation energy was calculated for 2 different basis sets at at 298.15 K and 0 K. For the calculation at 0 K, the sum of electronic and zero-point energies was used.

Activation energies in kcal/mol

	HF/3-21G		B3LYP/6-31(d)		Experimental
	0K	298.15K	0K	298.15K	0K
ΔE chair	45.70	44.69	34.08	33.12	33.5 ± 0.5
ΔE boat	55.60	54.77	41.98	41.32	44.7 ± 2.0

The table above shows that the chair transition state has a lower activation energy than the boat transition state. The activation energy for the chair transition state at 0K with B3LYP theory matches best with the experimental value. It also shows that the higher level of theory gives a closer value to the experimental that HF/3-21G basis set.

The Diels Alder Cycloaddition

Ethene and butadiene cycloaddition

Ethene and cis-butadiene were drawn in Gaussian and optimised separately using the AM1 semi-empirical molecular orbital method, which is a low level of theory.

MOs

	ethene	cis-butadiene
LUMO
HOMO

The diagrams show that the HOMO of ethene and LUMO of butadiene are symmetric in respect to the plane perpendicular to the C-C bond, and the LUMO of ethene and the HOMO of butadiene are antisymmetric with respect to the plane perpendicular to the C-C bond. These respective molecular orbitals have matching symmetry and so can interact with each other, leading to allowed transitions.

Transition state

The transition state for the Diels alder reaction between ethene and cis-butadiene. First, guess of the transition state was drawn first, an envelope shape with dotted lines between the atoms that will form a new bond in the reaction. A gaussian template of bicylco-2,2,1-heptane was used, the bridging CH₂ was removed and 2 bonds were changed to dotted lines. Based on the tutorial completed earlier, the 2 step method, done be freezing the coordinates was chosen. An alternative method can be used by calculating the force constant matrix (the Hessian), however the guess transition structure has to be close to the true structure otherwise the calculation won't work.

The guess transition structure was drawn and optimized for a transition state (Berny). The frequency was also calculated. The force constants were calculated once and Opt=NoEigen to ensure that the calculation stops crashing if more than one imaginary calculation is detected, this can happen if the guess structure is far off from the correct structure.

TS vibrations

Imaginary frequency -525cm-1	Lowest positive frequency 167cm-1

The imaginary frequency shows the vibration that is associated with the transition state reaction path. We can see that the formation of the 2 bonds is synchronous, this is expected as the reaction proceeds through a pericylic reaction. Comparison of the lowest positive shows that this vibration is asynchronous, however this is only a vibration, not the reaction pathway that proceeds.

TS MOs

HOMO	LUMO

Both the HOMO and LUMO are symmetric with respect to the plane perpendicular to the C=C bond in butadiene. The MOs involved in forming this transition state are the HOMO of butadiene and the LUMO of ethene.

Bond lengths

Bond	Distance in Å
σ C-C bond in TS	2.27
sp2 C-C	1.47
sp3 C-C	1.54
Van der waals radius of Carbon	1.7

The distance of the partically formed σ C-C bonds in the transition state are 2.27Å, which matches with the literature. This distance is longer than the sp3 and sp2 C-C bond lengths but shorter than the sum of the Van der Waals radii for 2 carbons, this shows that there is an interaction between the carbon atoms

Calculation with a higher basis set

Labeled image of Diels alder transition state with bond lengths here (using AM1-semi empirical molecular method).

The transition state was reoptimised with a higher level of theory using the B3LYP/6-31G(d) basis set, one of the reasons is because it takes the effect of electron correlation into account.. This is a more expensive method (i.e. it takes longer to calculate), However it is expected to be more accurate and match more closely with experimental values. A labelled image of the transition state using this theory can be seen here. Looking at both structures they look the same, comparision of the bond lengths shows there is a slight difference in the bond lengths. The distances C1-C2 and C3-C4 are longer with B3LYP theory at 2.27Å, compared to 2.21Å using the semi-empirical method. There is also a difference in the total energy of the transition state. This shows that using different levels of theory can lead to slightly different transition structures. The higher level of theory has optimised the transition state more effectively. The total energy with the semi-empirical method is -231.60320829 a.u., optimisation with using B3LYP leads to a total energy of -234.54389647 a.u. Even though the higher level of theory has calculated a lower total energy, the energies cannot be compared as different basis sets have been used and so the energies cannot be used to tell which method is more accurate. Although the B3LYP basis set is more accurate is was much more expensive, it took much longer to run than the AM1 basis set and so when deciding which basis set to use, there will always be a trade off.

Reaction with cyclohexa-1,3-diene and maleic anhydride

This cycloaddition forms both the exo and endo adducts. These structures were found and optimised using the QTS2 method. Both the reactants, cyclohexa-1,3-diene and maleic anhydride, and the exo product were drawn and optimised separately using the AM1 semi empirical molecular method. The optimised structures were used as the reactants and products in the QTS2 method. The structures were optimised and the frequency calculated with TS(QTS2). The labelled reactants and exo product can be seen. This process was repeated to form the endo product (labelled reactants and product). The reactants had to be moved so they resembled the transition state, for the endo reactants, the maleic anhydride was rotated by 180^o in comparison with the exo reactants. If the reactants were not aligned as desired the wrong product would be generated.

Diels Alder products

Exo	Endo

Exo

TS	TS vibration	HOMO	LUMO	TS total energy
				-0.05041982 a.u.

The animation shows the imaginary frequency at -812cm^-1. Here the synchronous bond forming can be seen. As the carbon atoms involved in the bond formation between cyclohexa-1,3-diene and maleic anhydride come closer together, the double bonds in cyclohexa-1,3-diene lengthen as the double bond breaks to form a single bond, and the single bond shortens as a double bond forms. As the bond forms the cyclohexa-1,3-diene ring puckers and is no longer planar.

Endo

TS	TS vibration	HOMO	LUMO	TS total energy
	‎			-0.0515079 a.u.

The animation shows the vibration associated with the reaction pathway at -806cm^-1. Again the bonds that are being formed can be seen, and they are synchronous. The animation shows the lengthening of the C=C bond as it breaks to form a single bond and the shortening of the C-C bond as a double bond is formed. The puckering of the ring and loss of planirity can also be seen.

The LUMOs of the exo and endo and the HOMO are antisymmetric while the HOMO of the endo is symmetric respectively.

The (O=C)O(C=O) fragment is anti-symmetric to C=C in the maleic anhydride and there is a nodal plane perpendicular to the C=C bond in the maleic anhydride.

Calculation with a higher basis set

The transition states were re-optimised using a higher level of theory, DFT/B3LYP/6-31G(d).

Activation energies in kcal/mol

	HF	B3LYP
Exo	39.05440313	29.69988174
Endo	19.80346158	15.72460370

This table shows that at both levels of theory the activation energy is lower for the endo product and so it is the kinetic product. This can also be seen when looking at the total energy of the transition state. The endo transiiton state is lower in energy than the exo and so the exo product is the thermodynamic product. The calculation of the activation energy shows that in this case, calculating at different theory levels has a significant effect.

The structures of the transition states with the different basis sets used look very similar however on closer inspection it can be seen that there are slight differences, as shown below.

Labelled diagram of exo TS

Exo TS

Bond	AM1	B3LYP
C6-C7/C3-C8	2.170405 Å	2.29058 Å

Labelled diagram of endo TS

Endo TS

bond	AM1	B3LYP
C3-C12/C4-C15	2.1624 Å	2.26831 Å

In both the exo and endo transition states, the higher level theory calculates slightly longer interactions betwen C6-C7 and C3-C8.

The endo product predominates as it is the kinetic product, this is partially due to the secondary orbital overlap (SOI) effects. These consist of mixing of orbitals which lowers the energy of the orbitals and hence the structure. This can be seen in the endo product when measuring some bond distances. Some measured bond lengths include C2-C13 = 3.0Å, C2-C18 = 3.2 Å, C1-C18 = 2.4 Å, C3-C12. These are all longer than bonds but shorter than the sum of the Van der Waals radii of carbon. These bonds are between the (O=C)O(C=O) fragment and the -CH=CH- fragment in the diene. The endo TS has this extra interaction and stabilisation whereas the exo does not. The distances between the CH₂-CH₂- and the(O=C)O(C=O)fragment are longer than the sum of the Van der Waals. The endo may also be the favoured product as there may be steric repulsions in the exo TS between the (O=C)O(C=O)CH₂-CH₂- fragment.

Conclusion

This study involved the investigation of several different methods using Gaussian, including the calculating the force constant matrix, frozen coordinate method and the QTS2 method. Different anti and gauche conformations of 1,5-hexadiene were drawn and the energies calculated. The Cope reaction was investigated and the chair and boat transition structure were optimised, it was found that the chair transition state has a lower activation energy than the boat.

The Diels Alder cycloaddition was also investigated. The AM1 semi-empirical molecular model was used initially and then the structures were re-optimised using a higher level of theory B3LYP/6-31(d). The transition states were optimised and the HOMO and LUMO MOs were visualized and the symmetry determined to explain which transitions were allowed. The regioselectivity of the Diels Alder was investigated and inspection of the frontier ortibals showed that the endo product was the favoured product due to SOIs and a lower activation energy. The endo product is the kinetic product while the exo is the thermodynamic.

Further investigation could include re-optimisation with even higher levels of theory.