Rep:Mod:ECN0511

Name: Estella Chin Ning
CID: 00697238

Optimising a BH₃ Molecule

3-21G Calculation

The results of the BH₃ 3-21G optimisation are summarised in Table 1 below.

Table 1: BH₃ 3-21G Optimisation
Link to log file of 3-21G Optimised BH₃ Molecule
File Type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	3-21G
Final energy	-26.46226429 a.u.
RMS gradient norm	0.00008851 a.u.
Dipole moment	0.00 D
Point group	C_S
Time taken for calculation	18.0 seconds

The expected point group symmetry of D_3h is not attained in the optimisation calculation above. This is because higher accuracy calculations are required to attain the correct point group symmetry of the BH₃ molecule. In addition, the gradient is less than 0.0001 (expected gradient = 0 for a stationary point), indicating that the molecule has indeed been optimised.

  Item               Value     Threshold  Converged?
 Maximum Force            0.000220     0.000450     YES
 RMS     Force            0.000106     0.000300     YES
 Maximum Displacement     0.000940     0.001800     YES
 RMS     Displacement     0.000447     0.001200     YES
 Predicted change in Energy=-1.672479D-07
 Optimization completed.
    -- Stationary point found.

The table above shows that the forces have converged, meaning that for a small displacement, the energy does not change. This further confirms the successful optimisation of the molecule.
The total energy and RMS Gradient of each optimisation step is shown in Figure 1 and 2 respectively.

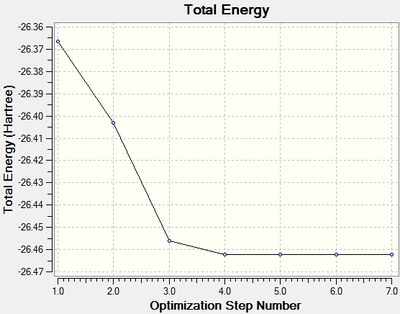
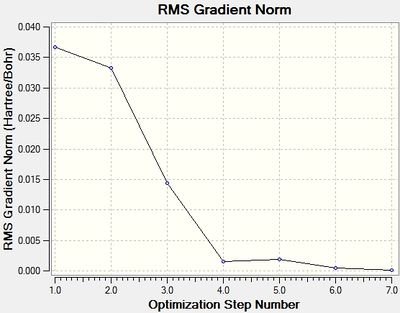
The last structure of the optimisation step has the most negative energy and the smallest gradient, suggesting that it is the energy minima structure.

6-31G (d,p) Calculation

The results of the 6-31G (d,p) optimisation are summarised in Table 2 below.

Table 2: BH₃ 6-31G (d,p) Optimisation
Link to log file of 6-31G (d,p) Optimised BH₃ Molecule
File Type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-26.61532360 a.u.
RMS gradient norm	0.00000009 a.u.
Dipole moment	0.00 D
Point group	C_S
Time taken for calculation	11.0 seconds

The expected point group symmetry of D_3h is not attained in the optimisation calculation above. This is because higher accuracy calculations are required to attain the correct point group symmetry of the BH₃ molecule. In addition, the gradient is less than 0.0001 (expected gradient = 0 for a stationary point), indicating that the molecule has indeed been optimised.

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000002     YES
 RMS     Force            0.000000     0.000001     YES
 Maximum Displacement     0.000001     0.000006     YES
 RMS     Displacement     0.000001     0.000004     YES
 Predicted change in Energy=-2.827323D-13
 Optimization completed.
    -- Stationary point found.

The table above shows that the forces have converged, meaning that for a small displacement, the energy does not change. This further confirms the successful optimisation of the molecule.

Optimised B-H Bond Distance: 1.19 Å
Literature B-H Bond Distance^[1] : 1.19 Å
Optimised H-B-H Bond Angle: 120.0 °
There is good corroboration between the calculated B-H bond distance and that found in literature. In addition, the H-B-H bond angle is 120.0 ° as would be expected for a BH₃ molecule which has the D_3h point group, confirming the accuracy of the optimisation calculations.

Total energy for the 3-21G Optimised Structure: -26.46226429 a.u.
Total energy for the 6-31G (d,p) Optimised Structure: -26.61532360 a.u.
Note that the energies of the 3-21G and 6-31G (d,p) optimised structure cannot be compared as different basis sets were used.

Optimising a GaBr₃ Molecule

LanL2DZ Calculation

The results of the LanL2DZ optimisation are summarised in Table 3 below.

Table 3: GaBr₃ LanL2DZ Optimisation
Link to log file of LanL2DZ Optimised GaBr₃ Molecule
Link to D-Space
File Type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	LANL2DZ
Final energy	-41.70082783 a.u.
RMS gradient norm	0.00000016 a.u.
Dipole moment	0.00 D
Point group	D_3h
Time taken for calculation	27.6 seconds

The gradient is less than 0.0001 (expected gradient = 0 for a stationary point), indicating that the molecule has indeed been optimised.

 Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000003     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-1.282690D-12
 Optimization completed.
    -- Stationary point found.

The table above shows that the forces have converged, meaning that for a small displacement, the energy does not change. This further confirms the successful optimisation of the molecule.

Optimised Ga-Br Bond Distance: 2.35 Å
Literature Ga-Br Bond Distance^[2] : 2.3525 Å
Optimised Br-Ga-Br Bond Angle: 120.0 °

There is good corroboration between the calculated Ga-Br bond distance and that found in literature. In addition, the Br-Ga-Br bond angle is 120.0 ° as would be expected for a GaBr₃ molecule which has the D_3h point group, confirming the accuracy of the optimisation calculations.

Optimising a BBr₃ Molecule

6-31G (d,p) and LanL2DZ Calculation

The results of the 6-31G (d,p) and LanL2DZ optimisation are summarised in Table 4 below.

Table 4: BBr₃ 6-31G (d,p) and LanL2DZ Optimisation
Link to log file of Optimised BBr₃ Molecule
Link to D-Space
File Type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	GEN (6-31G (d,p) and LanL2DZ)
Final energy	-64.43645388 a.u.
RMS gradient norm	0.00000943 a.u.
Dipole moment	0.00 D
Point group	C_S
Time taken for calculation	39.3 seconds

The expected point group symmetry of D_3h is not attained in the optimisation calculation above. This is because higher accuracy calculations are required to attain the correct point group symmetry of the BBr₃ molecule. In addition, the gradient is less than 0.0001 (expected gradient = 0 for a stationary point), indicating that the molecule has indeed been optimised.

      Item               Value     Threshold  Converged?
 Maximum Force            0.000016     0.000450     YES
 RMS     Force            0.000010     0.000300     YES
 Maximum Displacement     0.000067     0.001800     YES
 RMS     Displacement     0.000040     0.001200     YES
 Predicted change in Energy=-1.574159D-09
 Optimization completed.
    -- Stationary point found.

The table above shows that the forces have converged, meaning that for a small displacement, the energy does not change. This further confirms the successful optimisation of the molecule.

Optimised B-Br Bond Distance: 1.93 Å
Literature B-Br Bond Distance ^[3]: 1.893 Å

Optimised Br-B-Br Bond Angle: 120.0 °

There is good corroboration between the calculated B-Br bond distance and that found in literature. In addition, the Br-B-Br bond angle is 120.0 ° as would be expected for a BBr₃ molecule which has the D_3h point group, confirming the accuracy of the optimisation calculations.

Comparing the Bond Distances of BH₃, BBr₃ & GaBr₃

The summary of the different bond distances between BH₃, BBr₃ & GaBr₃ is shown in Table 5 below.

Table 5: Comparison of Bond Distances
Molecule	Bond Distance (Å)
BH₃	1.19
BBr₃	1.93
GaBr₃	2.35

The bond distances increase in the order: B – H (1.19 Å) > B – Br (1.93 Å) > Ga – Br (2.35 Å).

Comparing the bond distances of B – H and B – Br where the central atom (B) is kept constant, when the ligand is changed from H to Br, the bond distance increases. Both H and Br have 1 unpaired electron; the electronic configuration of H is 1s¹, while that of Br is [Ar] 4s²3d¹⁰4p⁵, which allows the formation of a covalent bond with B. However, this causes the B – H bond to have a larger s-character than the B – Br bond, where the unpaired electron from the Br is from the 4p orbital. In simpler terms, since the atomic size of the H ligand is smaller than that of the Br ligand, the Br atomic orbitals are more diffused, hence there is better orbital overlap between B and H as compared to B and Br, leading to the formation of stronger and shorter B – H bonds than B – Br bonds.

Similarly, by comparing the bond distances of B – Br and Ga – Br where the ligand (Br) is kept constant, when the central atom is changed from B to Ga, the bond distance increases. Both B and Ga belong to Group 13 of the periodic table and hence they have similar chemical bonding properties. However, B and Ga are found in Period 2 and 4 of the periodic table respectively, hence, B has a smaller atomic size and fewer atomic orbitals than Ga. This causes the B – Br bond to be shorter and stronger than the Ga – Br bond, as the Ga atomic orbitals are more diffused and hence the B – Br bond is formed closer to the central atom atomic nucleus than that of the Ga – Br bond.

A chemical bond can be defined as the attractive interactions between two atoms, which are normally attributed to electrostatic forces of attraction between the oppositely-charged induced dipoles of 2 atoms, or between 2 ions. In the optimisation process of the molecule, bonds are not observed between the central and ligand atoms in Gaussview. This does not indicate the absence of bonds between the atoms; it just shows that according to calculations, the atoms are too far apart as compared to a normal covalent bond length. In fact, since the atoms do not have the same electronegativities, one is bound to induce a dipole in the other, causing some form of interaction. The absence of the indicated bonds may just suggest that the atoms are too weakly bonded to be considered as sharing a covalent bond.

BH₃ Frequency Analysis

Frequency Calculation

The results of the 6-31G (d,p) frequency calculations are summarised in Table 6 below.

Table 6: BH₃ 6-31G (d,p) Frequency Calculations
Link to log file of Frequency analysis of BH₃
Link to D-Space
File Type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-26.61532364 a.u. (Same (up to last 2 d.p.) as that recorded in optimisation step)
RMS gradient norm	0.00000001 a.u.
Dipole moment	0.00 D
Point group	D_3h
Time taken for calculation	5.0 seconds

The gradient is less than 0.0001 (expected gradient = 0 for a stationary point), indicating that the molecule has indeed been optimised.

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000002     YES
 RMS     Force            0.000000     0.000001     YES
 Maximum Displacement     0.000000     0.000006     YES
 RMS     Displacement     0.000000     0.000004     YES
 Predicted change in Energy=-1.040964D-15
 Optimization completed.
    -- Stationary point found.

The table above shows that the forces have converged, meaning that for a small displacement, the energy does not change. This further confirms the successful optimisation of the molecule.

Low frequencies ---   -9.3484   -9.3330   -0.0724    0.0010    0.5365    2.5464
Low frequencies --- 1162.9903 1213.1496 1213.1498

The low frequencies are within the range of ± 15 cm^-1 and close to 0, indicating that the method employed in the frequency calculations was sufficiently accurate.

Summary of BH₃ Vibrations

The summary of BH₃ vibrational modes can be found in Table 7 below.

Table 7: Vibrational modes of BH₃
No.	Description	Frequency (cm^-1)	Intensity	Symmetry D_3h Point Group
1.	All the H atoms move up and down together in a concerted motion	1163	93	A₂"
2.	All the H atoms move towards and away from each other in a concerted motion, from left to right	1213	14	E'
3.	2 H atoms move towards and away from each other in a concerted motion, from left to right	1213	14	E'
4.	All the H atoms move in and out together in a concerted motion, the B atom is stationary	2583	0	Totally symmetric A₁'
5.	2 H atoms move in and out in an alternating motion	2716	156	E'
6.	2 H atoms move in and out in a concerted motion, alternating with the in and out motion of the last H atom	2716	126	E'

Infrared (IR) Spectrum

The infrared spectrum of GaBr3 is illustrated in Figure 3 below.

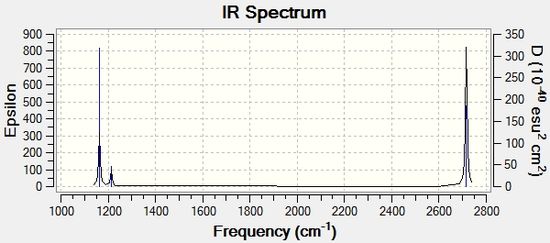
Although there are a total of 6 vibrational modes, only 3 corresponding peaks are present in the IR spectrum. This can be attributed to the fact that vibrational modes 2 and 3 vibrate at the same frequency (1213.15 cm^-1) and vibrational modes 5 and 6 vibrate at the same frequency (2715.66 cm^-1), giving rise to overlapping peaks in the infrared spectrum. Vibrational modes with the same frequency are called degenerate modes, as the vibrations are associated with the same energy. In addition, only vibrations that cause a change in the overall dipole moment of the molecule will give rise to peaks in the infrared spectrum. For the A₁' totally symmetric mode, there is no change in overall dipole moment associated with the vibration and hence the intensity of the peak in the infrared spectrum is '0'. Thus, there are 3 infrared peaks in total.

GaBr₃ Frequency Analysis

Frequency Calculation

The results of the GaBr₃ LANL2DZ frequency analysis are summarised in Table 8 below.

Table 8: GaBr₃ LANL2DZ frequency analysis
Link to log file of Frequency analysis of GaBr₃
Link to D-space
File Type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	LANL2DZ
Final energy	-41.70082783 a.u. (Same (up to last 2 d.p.) as that recorded in optimisation step)
RMS gradient norm	0.00000011 a.u.
Dipole moment	0.00 D
Point group	D_3h
Time taken for calculation	21.9 seconds

The gradient is less than 0.0001 (expected gradient = 0 for a stationary point) and close to 0, indicating that the molecule has indeed been optimised.

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000002     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
 Predicted change in Energy=-6.142862D-13
 Optimization completed.
    -- Stationary point found.

The table above shows that the forces have converged, meaning that for a small displacement, the energy does not change. This further confirms the successful optimisation of the molecule.

 Low frequencies ---   -0.5252   -0.5247   -0.0024   -0.0010    0.0235    1.2010
 Low frequencies ---   76.3744   76.3753   99.6982

The low frequencies are within the range of ± 15 cm-1, indicating that the method employed in the frequency calculations was sufficiently accurate.
The lowest "real" normal mode of GaBr₃ is the E' mode at 76 cm^-1.

Summary of Vibrations

The summary of GaBr₃ vibrational modes can be found in Table 9 below.

Table 9: Vibrational modes of GaBr₃
No.	Description	Frequency (cm^-1)	Intensity	Symmetry D_3h Point Group
1.	All the Br atoms move towards and away from each other in a concerted motion, from left to right	76	3	E'
2.	2 Br atoms move towards and away from each other in a concerted motion, from left to right	76	3	E'
3.	All the Br atoms move up and down together in a concerted motion	100	9	A₂"
4.	All the Br atoms move in and out together in a concerted motion, the Ga atom is stationary	197	0	Totally symmetric A₁'
5.	2 Br atoms move in and out in an alternating motion, while the Ga atom moves up and down	316	57	E'
6.	2 Br atoms move towards and away from the central Ga atom in a concerted motion, alternating with the in and out motion of the last Br atom	316	57	E'

Infrared (IR) Spectrum

The infrared spectrum of GaBr₃ is illustrated in Figure 4 below.

Comparing Vibrational Frequencies

The comparison table between the vibrational frequencies of BH₃ and GaBr₃ is shown in Table 10 below.

Table 10: Comparison between the vibrational frequencies of BH₃ and GaBr₃
No.	Symmetry D_3h Point Group	Description	BH₃		GaBr₃
No.	Symmetry D_3h Point Group	Description	Vibration	Frequency (cm^-1)	Vibration	Frequency (cm^-1)
1.	A₂"	All the 3 substituent atoms move up and down together in a concerted motion		1163		100
2.	E'	All the substituent atoms move towards and away from each other in a concerted motion, from left to right		1213		76
3.	E'	2 substituent atoms move towards and away from each other in a concerted motion, from left to right		1213		76
4.	A₁'	All the substituent atoms move in and out together in a concerted motion		2583		197
5.	E'	2 substituent atoms move in and out in an alternating motion		2716		316
6.	E'	2 substituent atoms move in and out in a concerted motion, alternating with the in and out motion of the last substituent atom		2716		316

As evident from the summary table, the frequency values for BH₃ are much larger than that of GaBr₃. As frequencies are directly proportional to the bond strength of the molecule, higher frequencies of BH₃ suggests that the B – H bond is much stronger than the Ga – Br bond. This corresponds to the difference in the optimised calculated bond strength between B – Br and Ga –Br, as shown in Table 5 above.

There has been a reordering of modes between the A₂” and 2 degenerate E’ modes. For BH₃, the doubly degenerate E’ modes vibrate at higher frequency, while for GaBr₃, the A₂" mode vibrates at higher frequency.

Both the BH₃ and GaBr₃ infrared spectra have 3 peaks, despite having 6 vibrational modes. This is due to the presence of 2 degenerate (E’) vibrational modes and a totally symmetric A₁’ vibrational mode which has an infrared peak at 0 intensity, reasons of which have been explained before.

For both spectra, the A₂” and 2 degenerate E’ modes vibrate at similar lower frequencies, while the A1’ and the other 2 degenerate E’ modes vibrate at similar higher frequencies. This is because the A₂” and the 2 degenerate E’ modes (No. 2 and 3 in the table above) are bending vibrational modes (wagging and scissoring respectively), which are relatively low energy vibrations and hence produce low frequencies. In contrast, the A₁’ mode and the other 2 degenerate E’ modes (No. 5 and 6 in the table above) are high energy stretching modes, the former being a symmetrical stretching vibrational mode, while the latter 2 are asymmetrical stretching modes. Stretching vibrational modes are relatively higher in energy than the bending modes. Hence, the A₁’ and E’ modes have higher energy frequencies as compared to the A₂” and E’ modes.

The chosen method determines the type of approximations that are made in solving the Schrodinger equation, while the basis set determines the accuracy of the optimisation process. These provide the potential energy surface on which optimisation and frequency calculations are made on. Optimisation analysis calculations provide the stationary points of a potential energy surface of a particular molecule, that is, the Schrodinger equation is solved for the nuclear and electronic positions at different molecular coordinates to find the lowest energy configuration. Frequency analysis calculations provide the second derivative of that stationary point derived from the optimisation in the same potential energy surface. Hence, it is vital to use the same method and basis set since both the optimisation and frequency calculations are based on the same optimised potential energy surface; using a different set of method and basis sets will cause the frequency calculations to be inaccurate as it will now be based on a different potential energy surface.

A frequency analysis provides information whether the optimised stationary point is a minimum point, maximum point, or a point of inflection. Frequencies are the second derivatives of a stationary point; positive frequencies indicate a minimum stationary point, while negative frequencies indicate a maximum stationary point. Since we are looking for the lowest energy configuration, i.e. a minimum point, the frequencies should be positive.

The "Low frequencies" represent the translational and rotational degrees of freedom of a given molecule; they are the "-6" component in the "3n-6" calculations of vibrational degrees of freedom for a non-linear molecule, or the "-5" component in the "3n-5" calculations of vibrational degrees of freedom for a linear molecule, where "n" represents the number of atoms in the molecule.

Molecular Orbitals of BH₃

The Molecular Orbital diagram of BH₃ is shown in Figure 5 below, which shows the similarities between the real and expected LCAO MOs.

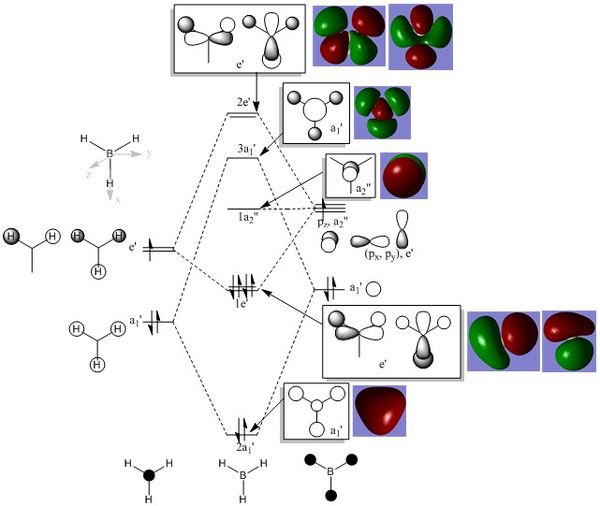
There are no significant differences between the real and expected LCAO MOs. As such, it can be inferred that qualitative MO theory is accurate in predicting the shapes, orientations and phases of actual molecular orbitals. This is especially useful as we now have a better picture of the electron density present in a given molecule.
N.B. The totally symmetric 1A₁' molecular orbital was generated, although this is not seen in the MO diagram drawn which only depicts valence electrons.

NH₃

Optimisation: 6-31G (d,p) Calculation

The results of the NH₃ 6-31G (d,p) Optimisation can be found in Table 11 below.

Table 11: NH₃ 6-31G (d,p) Optimisation
Link to the log file of 6-31G(d,p) Optimised NH₃ Molecule
File Type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-56.55776872 a.u.
RMS gradient norm	0.00000013 a.u.
Dipole moment	1.85 D
Point group	C₁
Time taken for calculation	9.0 seconds

The expected point group symmetry of C_3v is not attained in the optimisation calculation above. This is because higher accuracy calculations are required to attain the correct point group symmetry of the NH₃ molecule. In addition, the gradient is less than 0.0001 (expected gradient = 0 for a stationary point), indicating that the molecule has indeed been optimised.

 Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000002     YES
 RMS     Force            0.000000     0.000001     YES
 Maximum Displacement     0.000001     0.000006     YES
 RMS     Displacement     0.000001     0.000004     YES
 Predicted change in Energy=-2.600465D-13
 Optimization completed.
    -- Stationary point found.

The table above shows that the forces have converged, meaning that for a small displacement, the energy does not change. This further confirms the successful optimisation of the molecule.

Frequency Analysis

The results of the NH₃ 6-31G (d,p) frequency analysis can be found in Table 12 below.

Table 12: NH₃ 6-31G (d,p) Frequency analysis
Link to log file of Frequency Analysis of NH₃
Link to D-Space
File Type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-56.55776872 a.u. (Same (up to last 2 d.p.) as that recorded in optimisation step)
RMS gradient norm	0.00000020 a.u.
Dipole moment	1.85 D
Point group	C₁
Time taken for calculation	33.9 seconds

The expected point group symmetry of C_3v is not attained in the optimisation calculation above. This is because higher accuracy calculations are required to attain the correct point group symmetry of the NH₃ molecule. In addition, the gradient is less than 0.0001 (expected gradient = 0 for a stationary point), indicating that the molecule has indeed been optimised.

       Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000002     YES
 RMS     Force            0.000000     0.000001     YES
 Maximum Displacement     0.000002     0.000006     YES
 RMS     Displacement     0.000001     0.000004     YES
 Predicted change in Energy=-8.193705D-13
 Optimization completed.
    -- Stationary point found.

The table above shows that the forces have converged, meaning that for a small displacement, the energy does not change. This further confirms the successful optimisation of the molecule.

Low frequencies ---   -8.2887   -6.5533   -4.4302    0.0005    0.0008    0.0014
Low frequencies --- 1089.3394 1693.9228 1693.9270

The low frequencies are within the range of ± 15 cm-1 and close to 0, indicating that the method employed in the frequency calculations was sufficiently accurate.

MO Analysis

Link to the log file
Link to D-Space

NBO Analysis

The NH₃ NBO charge distribution is illustrated in Figure 6 below.

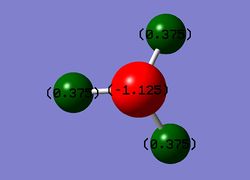
Charge Distribution: -1.125 - 1.125
Specific NBO charge for Nitrogen: -1.125
Specific NBO charge for Hydrogen: 0.375

NH₃BH₃

Optimisation: 6-31G (d,p) Calculation

The results of the NH₃BH₃ 6-31G (d,p) Optimisation can be found in Table 13 below.

Table 13: NH₃BH₃6-31G (d,p)Optimisation
Link to log file of 6-31G(d,p) Optimised NH₃BH₃ Molecule
File Type	.log
Calculation type	FOPT
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-83.22468911 a.u.
RMS gradient norm	0.00000009 a.u.
Dipole moment	5.56 D
Point group	C₁
Time taken for calculation	44.0 seconds

The gradient is less than 0.0001 (expected gradient = 0 for a stationary point), indicating that the molecule has indeed been optimised.

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000002     YES
 RMS     Force            0.000000     0.000001     YES
 Maximum Displacement     0.000000     0.000006     YES
 RMS     Displacement     0.000000     0.000004     YES
 Predicted change in Energy=-1.593712D-14
 Optimization completed.
    -- Stationary point found.

The table above shows that the forces have converged, meaning that for a small displacement, the energy does not change. This further confirms the successful optimisation of the molecule.

Frequency Analysis

The results of the NH₃BH₃ 6-31G (d,p) frequency analysis can be found in Table 14 below.

Table 14: NH₃BH₃6-31G (d,p) frequency analysis
Link to log file of Frequency Analysis of NH₃BH₃
Link to D-Space
File Type	.log
Calculation type	FREQ
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy	-83.22468911 a.u. (Same (up to last 2 d.p.) as that recorded in optimisation step)
RMS gradient norm	0.00000009 a.u.
Dipole moment	5.56 D
Point group	C₁
Time taken for calculation	153.9 seconds

The gradient is less than 0.0001 (expected gradient = 0 for a stationary point), indicating that the molecule has indeed been optimised.

 Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000002     YES
 RMS     Force            0.000000     0.000001     YES
 Maximum Displacement     0.000001     0.000006     YES
 RMS     Displacement     0.000000     0.000004     YES
 Predicted change in Energy=-6.087130D-13
 Optimization completed.
    -- Stationary point found.

The table above shows that the forces have converged, meaning that for a small displacement, the energy does not change. This further confirms the successful optimisation of the molecule.

  Low frequencies ---   -2.8702   -1.3787   -0.0007    0.0008    0.0009    3.5768
 Low frequencies ---  263.3606  632.9766  638.4460

The low frequencies are within the range of ± 15 cm-1 and close to 0, indicating that the method employed in the frequency calculations was sufficiently accurate.

Comparison of Reaction Energies

The comparison table of reaction energies between NH₃, BH₃, and NH₃BH₃ can be found in Table 15 below.

Table 15: Comparison of NH₃, BH₃, and NH₃BH₃ reaction energies
E (NH₃) / a.u.	- 56.55776872
E (BH₃) / a.u.	- 26.61532360
E (NH₃BH₃) / a.u.	- 83.22468911
Energy Difference/ a.u.	- 83.22468911 - ( - 26.61532360 - 56.55776872) = - 0.05159679
Energy Difference = Association Energy / kJmol^-1	- 0.05159679 x 2625.50 = - 140 (Accuracy to 10 kJ/mol)
Dissociation Energy / kJmol^-1	140 (Accuracy to 10 kJ/mol)

As typical bond dissociation energies range from 100 kJmol^-1 to 500 kJmol^-1, the N - B bond dissociation energy in NH₃BH₃ of 140 kJmol^-1 is a sensible value. In addition, since the bond present between NH₃ and BH₃ can be considered as a weak, dative interaction, the relatively low bond dissociation energy calculated seems reasonable.

References

↑ CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 87th edn., 2006.
↑ CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 87th edn., 2006.
↑ CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 87th edn., 2006.

[1] CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 87th edn., 2006.

[2] CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 87th edn., 2006.

[3] CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, 87th edn., 2006.

[1]

[2]

[3]

Optimising a BH3 Molecule

3-21G Calculation

6-31G (d,p) Calculation

Optimising a GaBr3 Molecule

LanL2DZ Calculation

Optimising a BBr3 Molecule

6-31G (d,p) and LanL2DZ Calculation

Comparing the Bond Distances of BH3, BBr3 & GaBr3

BH3 Frequency Analysis

Frequency Calculation

Summary of BH3 Vibrations

Infrared (IR) Spectrum

GaBr3 Frequency Analysis

Frequency Calculation

Summary of Vibrations

Infrared (IR) Spectrum

Comparing Vibrational Frequencies

Molecular Orbitals of BH3

NH3

Optimisation: 6-31G (d,p) Calculation

Frequency Analysis

MO Analysis

NBO Analysis

NH3BH3

Optimisation: 6-31G (d,p) Calculation

Frequency Analysis

Comparison of Reaction Energies

References

Optimising a BH₃ Molecule

Optimising a GaBr₃ Molecule

Optimising a BBr₃ Molecule

Comparing the Bond Distances of BH₃, BBr₃ & GaBr₃

BH₃ Frequency Analysis

Summary of BH₃ Vibrations

GaBr₃ Frequency Analysis

Molecular Orbitals of BH₃

NH₃

NH₃BH₃