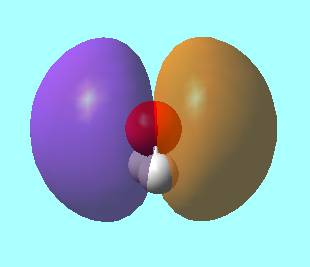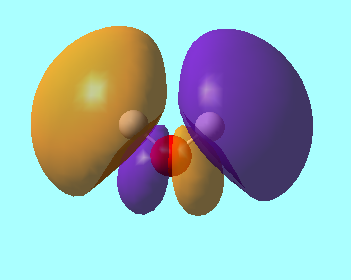Rep:Mod:ECF3842
NH3 Molecule
NH3 molecule |
Optimising NH3
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -56.55776873 a.u. |
| RMS Gradient Norm | 0.00000485 a.u. |
| Point Group | C3V |
N - H bond distance : 1.01798Å
Bond Angle : 105.741
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
The optimisation file is liked to here
Vibrational Analysis
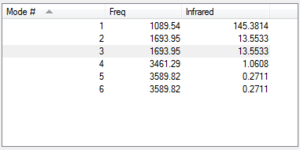
From the 3N-6 rule your would expect six modes of vibration, since NH3 has four atoms, and (3x4)-6 = 6 From the table above, it can be seen that vibrations 2 and 3 are the same energy, and the vibrations 5 and 6 are the same energy. This can be seen because their frequencies are the same. In the table above, the bending modes are the modes 1,2 and 3. The stretching modes are 3,4 and 5. The highly symmetric mode is mode 4 and the "umbrella" mode is mode 1. In the Infrared Spectrum of gaseous ammonia you would expect to see four bands, due to four different frequencies stated.
Charge Analysis
The charge on the nitrogen atom is -1.125D, and the charges on the hydrogen atoms is +0.375D.
N2 Molecule
N2 molecule |
Optimising N2
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -109.52412868 a.u. |
| RMS Gradient Norm | 0.00000060 a.u. |
| Point Group | D*H |
N-N bond distance : 1.10550Å
Bond Angle : 105.741°
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
The optimisation file is linked to here.
Vibrational Analysis

The image to the right shows the vibrational frequency for the N2 molecule. There is one mode of vibration and this corresponds to a stretching mode. There is only one mode because the molecule is a simple diatomic, that s linear so the number of modes is given by 3N-6, which in this case is (3x2)-6=1. It can be seen that the frequency of this mode of vibration is positive.
Molecular Orbitals for N2
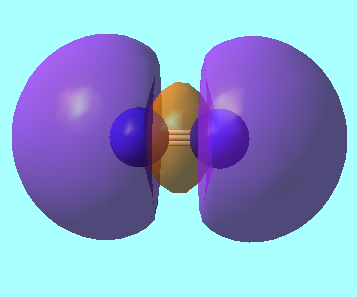
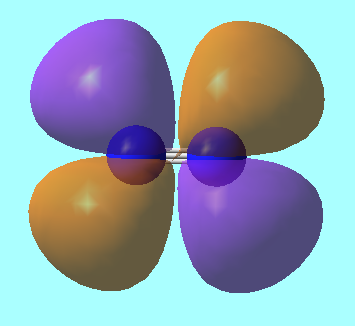
MO 3: 2s bonding MO of energy E=-1.12383 a.u.
MO 4: 2s antibonding MO of energy, E = -0.55342 a.u.
MO 5: pi MO from 2p orbitals of energy, E = -0.46240 a.u.
MO 7: HOMO from 2p sigma bonding orbitals of energy, E= -0.42688 a.u.
MO 8: LUMO from antibonding combination of perpendicular 2p orbitals of energy, E= -1.02412 a.u.
H2 Molecule
H2 molecule |
Optimising H2
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -1.17853936 a.u. |
| RMS Gradient Norm | 0.00000017 a.u. |
| Point Group | D*H |
H-H bond length = 0.74279Å
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
The optimisation file is linked to here.
Vibrational Analysis

The image to the right shows the vibrational frequency for the H2 molecule. There is only one mode of vibration as it is a simple diatomic molecule, and this is a stretching mode. The frequency of this mode of vibration is positive. The frequency of this vibration is 4465.68cm-1 whereas the vibrational frequency for the N2 stetch is 2457.33cm-1. The reason for this is because although the N2 triple bond is much stronger than the H2 single bond, the reduced mass of the hydrogen molecule is much smaller than that of the nitrogen, which outweighs the difference in bond strength.
Finding the energy change of the Haber-Bosch reaction
The equation for this reaction is as follows: N2(g) + 3H2(g) -> 2NH3(g)
E(NH3)= -56.55776873 a.u.
2*E(NH3)= -113.11553746 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 a.u.
In kJ/mol,ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -146.48 kJ/mol
The ammonia is more stable than the two reactants, H2 and N2, as the energy of the ammonia is lower than that of each of the reactants. Also, this reaction is exothermic, meaning that energy is released upon the formation of NH3, suggesting that the ammonia is more stable than the reactants.
H2O molecule
Cl2 molecule |
Optimising H2O
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| Final Energy E(RB3LYP) | -76.41973740 a.u. |
| RMS Gradient Norm | 0.00006276 a.u. |
| Point Group | C2V |
Item Value Threshold Converged? Maximum Force 0.000099 0.000450 YES RMS Force 0.000081 0.000300 YES Maximum Displacement 0.000128 0.001800 YES RMS Displacement 0.000120 0.001200 YES
O-H bond length : 0.96522Å
H-O-H bond angle : 103.745°
The optimisation file is linked to here.
Vibrational Analysis
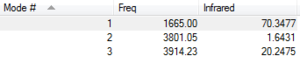
The image to the right shows the frequencies of the vibrational modes of H2O. There are three modes of vibration because H2O is a bent molecule so the number of vibrational modes is equal to 3N-6. As there are three atoms, the number of modes of vibration is (3x3)-6 = 3. The first bending mode at a frequency of 1665.0cm-1 is the 'wag' bending mode. The second vibrational mode at 3801.05cm-1 is the symmetric stretch and the third mode of vibration is the asymmetric stretch.
Charge Analysis
Since oxygen is more electronegative than hydrogen, the distribution of charge withing the molecule is not even. The charge on the oxygen is -0.944D and the charge on each hydrogen is +0.472D.
Molecular Obitals for H2O
MO 1: This is the 1s orbital of the oxygen atom. It has an energy of -19.13799 a.u., which is much lower than the energies of the other molecular orbitals for H2O. This orbital is so deep in energy that the 1s orbitals on the hydrogen are unable to interact with it.
MO 4: This is the molecular orbital with the fourth lowest energy for the H2O molecule. It is a sigma bonding orbital between the 1s orbitals on the hydrogen and the 2py orbital on the oxygen. The energy of this orbital is -0.37102 a.u.
MO 5: This molecular orbital is the HOMO. The only contribution to this orbital is the 2pz orbital so it is solely on the oxygen atom. The energy of this orbital is -0.29197 a.u.
MO 6: This molecular orbital is the LUMO. This orbital is an antibonding orbital with contributions from the 1s orbitals of the hydrogen and an sp3 hybridised orbital of the oxygen. It has an energy of 0.06538a.u.
MO 7: This molecular orbital is an antibonding orbital with contributions from the 1s orbitals on the hydrogen and the 2px orbital on the oxygen. It has an energy of 0.15127 a.u.