Rep:Mod:Dz1814

Introduction

Potential Energy Surface

A Potential Energy Surface (PES) models the energy of a system based on set parameters (usually the coordinates of the atoms), once generatred the gradient and curvature of different points along it can provide a lot of information about the chemical reaction. Physical meaning can be extracted from the surface by considering the stationary points along it - at such points the gradient is equal to zero:

• Minimas correspond to physically stable species. At these points all the force constants, in all dimensions, are negative. Surfaces are usually complex and exhibit several of these points, which are referred to as local minima apart from the lowest point of the surface - known as the global minima corresponding to the most stable state of the system.
• The transition state is the point of highest energy along the reaction coordinate, in a potential energy surface it is known as a saddle point and it separates the products from the reactants. It is important to remember that this is not a 'real' chemical species and cannot be isolated, instead it a state in which bonds are being partially formed and broken between the reactants during the process of forming the products.

21:19, 21 March 2017 (UTC) Good understanding here. You could have gone further and spoke about the second derivatives.

Abstract

This computational simulation aims to investigate 3 different Diels-Alder reactions, of increasing complexity, and one competing cheletropic reaction using a preliminary semi-empirical PM6 optimisation, followed by a more accurate Density Functional Theory (DFT) optimisation at the B3LYP/6-31G(d) level. An Intrinsic Reaction Coordinate (IRC) analysis along with a manual C-C bond length analysis allowed us to determine the nature of the reactions (i.e. concerted or step-wise) as well as visualise the path of the reactants during the transition state. Finally energy diagrams are generated and used to determine the preferred kinetic and thermodynamic products where appropriate.

Methods of Optimisation

3 different methods were employed in order to complete these simulations, each building on the last.
Method One is the fastest but the most unreliable method. Here we are required to a guess the transition state and manually set the bond distances between the fragments before optimising firstly to the PM6 level, then to the B3LYP/6-31G(d). This method can only be used when working with small systems with simple, easy to guess, (or known) transition states, it was adequate for exercise 1 where the reacting fragments were fairly simple but could not be used any further.
Method Two expands on method one. Again we must manually draw the transition state and hence some knowledge of it is required, however this time the reacting atoms are frozen in space prior to the optimisation. This allows the rest of the system to move and find the structure of minimal energy, putting it as close as possible to the transition state and giving us a better structure to optimise than our initial guess.
Method Three is more complicated and requires several extra steps before the optimisation can be performed, however it is the most reliable, and requires no knowledge of the transition state, which means it can be applied to many different molecules. Here we must start with either the reactants or the products and alter their bond lengths/angles to resemble the transition state. An optimisation to a minimum at the PM6 level then returns a structure closer to the transition state. If working from the product, the bonds which will form in the reaction are then broken and another optimisation to a minimum returns the reacting fragments in the correct orientation, finally the optimisations are performed such as in method one.

Exercise 1: Butadiene with Ethylene

550×162px

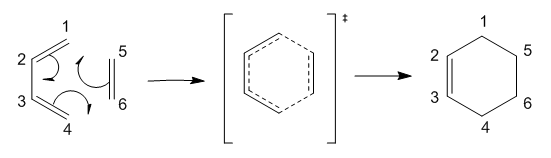
The first calculation was of a simple [4+2] concerted Diels-Alder reaction between butadiene and ethylene to give cyclohexene. This reaction yield only a single product sue to the un-substituted nature of the reactants, and hence no thermodynamic analysis was needed. The reactants, products and transition state were optimised at the PM6 and B3LYP/6-31G(d) levels.

MO diagram and orbital analysis

Ethylene	Butadiene	Transition state

The orbitals of the reactants were visualized in Gaussian, and used to construct the MO diagram bellow, the HOMO and LUMO provide all the needed information to describe this reaction and hence are the only orbitals shown in the diagram. The formed orbitals were found to be slightly destabilised relative to the starting fragment orbitals, this is rational as we are considering the transition state of the reaction, which is the point at which the system has the highest energy.

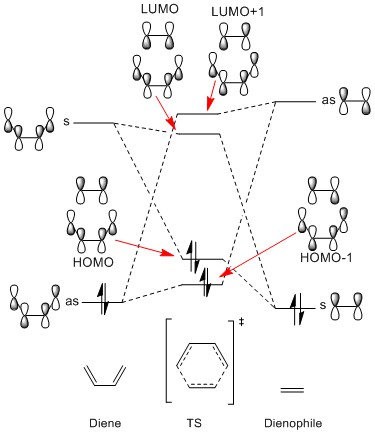
As can be seen in the diagram, the orbitals mix based on their symmetry labels ie:

• Butadiene HOMO + ethylene LUMO (symmetric)
• Butadiene LUMO + ethylene HOMO (asymmetric)

This is due to reactions only being 'allowed' when the interacting fragments are of the same symmetry- which also leads to a non-zero orbital overlap integral. Consequently a symmetric-asymmetric interaction would lead to an orbital overlap integral of zero - i.e. the orbitals would not mix and the reaction can be considered 'forbidden'.

The phases of the orbitals also plays an important role. When the fragments mix in phase there is a positive orbital overlap integral and the resulting mixed MO is of lower energy - this is how the HOMO and HOMO-1 are formed. Similarly, when the orbitals mix out of phase they have a negative orbital overlap and form mixed MO's of higher energy - i.e. the LUMO and LUMO+1.

The following mixing is an example of 'normal' demand Diels-Alder.

(Fv611 (talk) 17:48, 15 March 2017 (UTC) Very nice MO diagram (well done on assigning the correct relative energies to the MOs!), and very nice JMol scripting, but you are missing the symmetry labels on the transition state MOs.)

Imaginary and lowest positive vibration of the TS

The gifs bellow animate the imaginary and the first positive vibrations of the transition state (-526/cm and 136/cm respectively). The vibration at -526/cm shows the two terminal carbons of butadiene approach the two carbons of ethylene in the transition state, prior to the formation of the bonds. The retention of symmetry in both molecules during the bond formation process shows that the reaction is synchronous, which is as expected from a concerted reaction. Examination of the vibration at 136/cm shows the atoms twisting but not approaching eachother, which shows that this vibration mode does not contribute to bond formation, contrary to the previous.

(Fv611 (talk) 17:48, 15 March 2017 (UTC) As you stated earlier that you optimised it at both PM6 and B3LYP levels, it would have been better practice to make explicit that this one is B3LYP.)

C-C bond length analysis

C-C bond	Bond Length (Å)
	Reactants	Transition state	Product
C1-C2	1.335	1.383	1.501
C2-C3	1.468	1.407	1.338
C3-C4	1.335	1.383	1.501
C4-C6	N/A	2.272	1.540
C5-C6	1.327	1.386	1.541
C5-C1	N/A	2.272	1.540

Examining the bond lengths between the atoms at different stages of the reaction also gives an indication of the way the reaction proceeds. The double bonds between C1-C2, C3-C4 (butadiene) and C5-C6 (ethylene) all lengthen when going from reactants to TS to product. This indicates the transformation from double to single bonds and hence a change in hybridisation from sp3 to sp2, the relative changes of bond length are in excellent agreement with the typical values of these hybridisations. This is accompanied by a simultaneous shortening between C2-C3 as the new pi system is formed.

Literature values of typical bond lengths are shown bellow. They are in excellent agreement with the values produced in the computational simulation hence illustrating that this is a good tool to use for these approximations.

• $s{p}^3$ C-C: 1.54Å (c.f. C5-C1, C5-C6, C4-C6 in product)
• $s{p}^2$ C-C: 1.47Å (c.f. C2-C3 in reactants)
• $s{p}^2$ C=C: 1.34Å (c.f. C1-C2, C3-C4, C5-C6 in reactants and C5-C6 in product)

The Van der Waals radius for a carbon atom is 1.7Å. Since the lengths between the carbons of butadiene and ethylene in the transition state (C4-C6 and C5-C1) are shorter than 2xVDW radius we can safely assume that there is some sort of interaction occurring between the fragments. The fact that all these changes occur at the same time, and at similar magnitudes (i.e. C1-C2 and C3-C4 both change the same amounts) further supports the hypothesis that the reaction proceeds via a concerted mechanism. To further confirm this, the IRC of the reaction is shown (right), here, it is clear to see that the two new sigma bonds forming simultaneously.

Exercise 2: Cyclohexadiene and 1,3-Dioxole

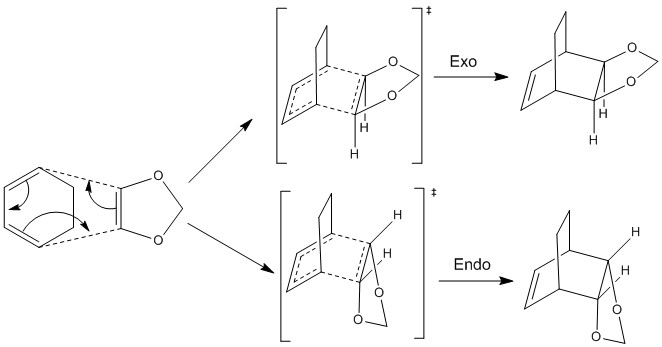
Method 3 was used for the second simulation which involved more complex reagents in another Diels-Alder reaction. The reagents were initially optimised at the PM6 level ensuring that neither displayed an imaginary frequency - it was necessary to break the symmetry to ensure that this requirement was met. In this reaction we must consider the orientation of attack of the molecules as it is now possible to form two different isomers, this was easily achieved by simple rotation of one of the reactants prior to optimisation of the transition state. The presence of two different isomers now gives a more interesting reaction profile and allows us to consider the thermodynamics and kinetics of the reaction. Both transition states were optimised at the PM6 level before optimisation at the B3LYP/6-31(d) level to speed up the process.

Analysis of the Molecular Orbitals

The HOMO and LUMO orbitals for the reactants and both transition states are shown in the tables bellow. The HOMO of the transition state is symmetric, and hence must be formed by mixing symmetric orbitals in order for the reaction to be allowed. From this we can conclude that the interacting orbitals are:

• 1,3-dioxole HOMO + cyclohexene LUMO (symmetric)

This orbital interaction is characteristic of an inverse demand Diels-Alder reaction. The dienophile in this simulation is electron rich due to the presence of the two adjacent oxygen atoms, whilst the purely hydrocarbon diene is relatively electron poor. The extra electron density in the dienophile raises the energy of both frontier orbitals, resulting in the LUMO being too high in energy to interact with the diene's HOMO as it would in a normal Diels-Alder.

Reactants
1,3-Dioxole
HOMO (s)		LUMO (as)
Cyclohexadiene
HOMO (as)		LUMO (s)

Transition States
Endo
HOMO (s)		LUMO (s)
Exo
HOMO (s)		LUMO (s)

(Nice table, but it would be good to see these MOs in an MO diagram to correlate them Tam10 (talk) 11:31, 23 March 2017 (UTC))

Thermodynamic Analysis

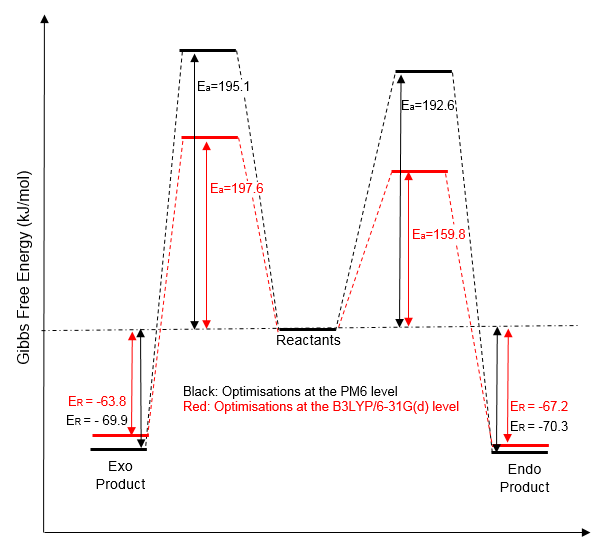
The activation and reaction energies for both products were calculated using both the PM6 and B3LYP/6-31G(d) levels and summarised in the above diagram (shown in black and red respectively) to show the differences produced by the two optimisation methods. It becomes obvious that the two methods produce different values for the activation and reaction energies, however their relative energy remains same (i.e. the exo- TS is always greater than the endo-, and the endo- product is always lower in energy than the exo-). It would therefore be sufficient to use the quicker PM6 calculation for a qualitative analysis of the reaction.

From the diagram above we can conclude that the endo- isomer is both the kinetic and thermodynamic product of this reaction due to its lower barrier of activation and larger (more negative) energy of reaction. Hence, we would expect this product to be dominate in both non-equilibrium and equilibrium conditions.

The stability of the endo- product can be understood by considering the orbital interactions in the transition state. As can be seen in the diagram to the right, the endo- product exhibits favorable secondary interactions between the lone pair of the oxygen (found in a p orbital) and the pi system of the diene, lowering the energy of the transition state and hence results in the reaction proceeding faster. This interaction is not possible in the exo- orientation as the oxygens are placed on the other side of the molecule, and hence this conformer exhibits only primary interactions and a higher energy transition state.

Nf710 (talk) 21:30, 21 March 2017 (UTC) The stability of the SSO contributions is only present for the TS, the product is lowered due to sterics.

(To add to what Nathan said here, we only talk about secondary orbital interactions regarding a transition state, where there is a primary interaction at the bonding site, and a secondary favourable interaction that helps to stabilise the TS. The interaction between the oxygen orbitals and the new alkene pi orbital does remain in the product however Tam10 (talk) 11:31, 23 March 2017 (UTC))

IRC Analysis

Finally the IRC for the formation of the endo- adduct is displayed (right), it clearly shows the synchronous nature of the reaction, showing that it is indeed concerted.

Nf710 (talk) 21:28, 21 March 2017 (UTC) You have made a mistake in the diagram, your file says 167.8 not 197. obviously it would be drawn wrong if those were the values. The diagram is a nice comparison of the methods. Your understating the ordering of thermo and kinetic is good.

Exercise 3: o-Xylylene and SO2

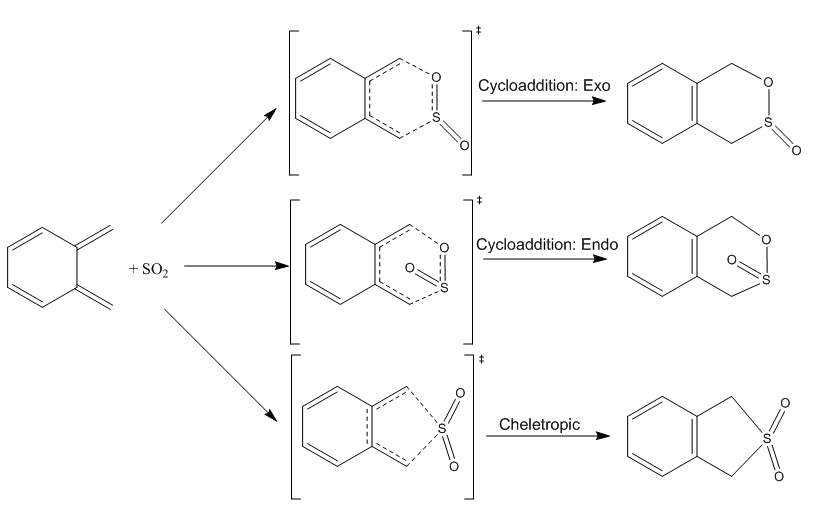
The final exercise used Xylylene and Sulfur Dioxide, which can react via either a Diels-Alder cycloaddition or a cheletropic reaction to yield 3 different products. The reactants, transition states and products were optimised at the PM6 level, the IRC of the three reactions were compared and a thermodynamic analysis was performed to establish the kinetic and thermodynamic products.

IRC Analysis

Gifs of IRC
Endo	Exo	Cheletropic

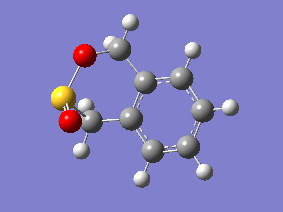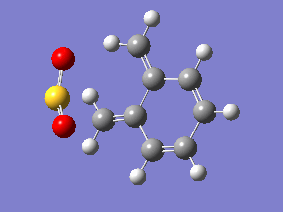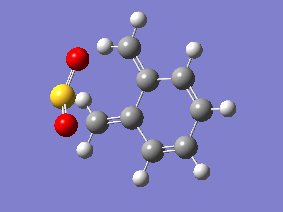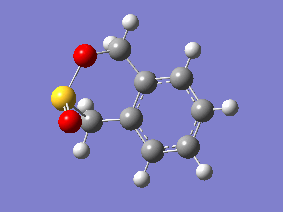
Examining the IRC gif's above shows us the main driving force for all these reactions - the aromitisation of the 6 membered ring in xylylene. We can also see that the Diels-Alder reaction proceeds in an asynchronous fashion with the new C-O bond forming slightly earlier than the new C-S bond, this shows that this cycloaddition reaction is not truly concerted. The opposite is seen in the cheletropic reaction, the terminal carbon atoms of xylylene approach the sulfur molecule and the 2 new sigma bonds are simultaneously formed, showing the synchronous nature of the concerted reaction.

Thermodynamic Analysis

The activation and reaction energies were calculated using a PM6 optimisation in the same way as in exercise 2 - it was decided to not use the B3LYP/6-31G(d) level as optimisation took much longer and PM6 was sufficient for a qualitative analysis. The reaction profiles for all 3 possible pathways were plotted on one diagram to allow for easier comparison.

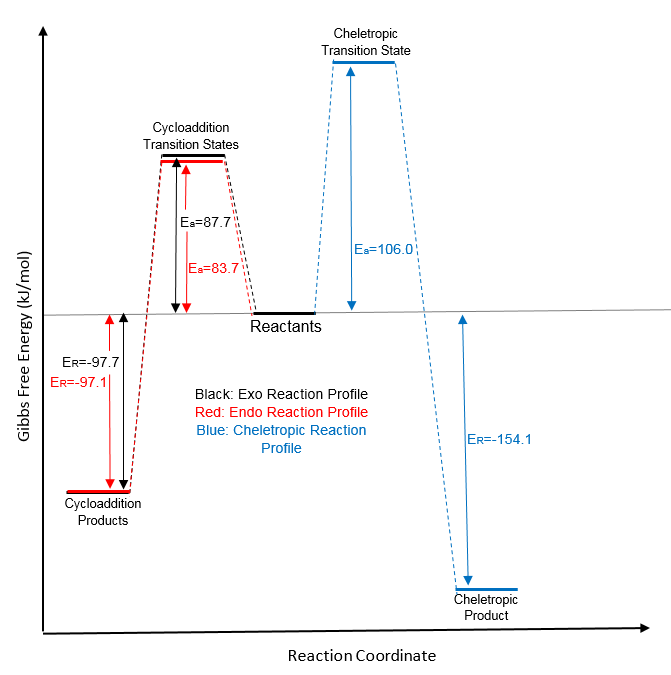
(This is an ideal example of what a reaction profile should look like. The data is clear and we know how the reactions are related. I'd recommend sticking to this sort of style for future work Tam10 (talk) 11:31, 23 March 2017 (UTC))

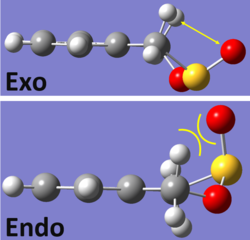
The left side of the graph illustrates the cycloaddition reactions which form the endo- and exo- products. It is clear that the endo- product (shown in red) has a lower activation energy and hence is the kinetically favored product - it would be expected to predominate if the reaction was to be carried out in non-equilibrium conditions as it will be the quickest to form. This is once again due to secondary orbital overlap between the non reacting oxygen atom and the pi system of the xylylene double bond.

Optimisation at this level gave very similar values for the energy of reaction for both the isomers, with the exo- being only slightly more stable suggesting that this is the thermodynamically preferred product. The reason for this is most likely to be steric clashes of the oxygen outside of the ring with hydrogen atoms in the endo- product (shown right). Due to the bending of the ring in the exo- adduct, this interaction is reduced. Hydrogens are small and therefore would result in only minimal steric hindrance, which could explain why the energy difference between the two isomers is so small.

The activation energies for the two cycloaddition pathways are fairly close to eachother in magnitude, therefore we can safely assume that a mixture of the two products would form when carrying out this reaction. Contrary to this, the cheletropic reaction (shown in blue) displays a much higher activation barrier, meaning the system would need a substantially larger input of energy to proceed via this path rather than the cycloaddition route. This could potentially allow us to minimise the formation of the cheletropic adduct by carefully controlling the amount of energy put into the system so that the minimum amount for cycloaddition is supplied, but not for the cheletropic path.

The simulation shows the cheletropic product to be the most thermodynamically favored of the three, indicated by the largest (most negative) energy of reaction, this is in good agreement with previous computational analysis . This is most likely due to the presence of the two S=O bonds rather than the presence of a S-O bond (such as in the cycloaddition product).

Alternative Xylylene Reaction

Theoretically it is possible for xylylene to react via its second cis-butene fragment which is found within the 6 membered ring (this site will be referred to as the secondary diene for ease of comparison). A simulation for this reaction was performed and optimised at the PM6 level so that the activation and reaction energies could be calculated in order to determine if the reaction is feasible. The IRC's for both isomers are displayed bellow. Both follow the same asynchronous path as the earlier reaction at the primary diene, with the C-O bond forming slightly earlier than the C-S bond, indicating that the reaction is not truly concerted.

Gifs of IRC
Endo	Exo

Analysis of Thermodynamics

Adduct	Activation Energy (kJ/mol)	Reaction Energy (kJ/mol)
Endo	113.9	-18.2
Exo	121.8	-22.7

(I don't think these are even exothermic reactions at this level of theory Tam10 (talk) 11:31, 23 March 2017 (UTC))

From the table above we can conclude that a reaction at this site would be both thermodynamically and kinetically unfavorable, due to it having an activation energy which is much greater than its reaction energy, hence we can safely assume none of these adducts would be formed. The decreased stability of the products is most likely due to the absence of an aromatic system, which is the main driving force in the reaction at the primary diene.

During the reaction the reacting carbons are displaced, moving towards the SO2 molecule, prior to forming the new bonds - this vibration is animated in the table bellow for both dienes in the endo- approach. Displacing the carbons within the ring (in the secondary diene attack) would require more energy due to the rigidity of the ring compared to that at the primary, where the carbons have more flexibility. This could be an explanation for the increased activation energy of this approach.

Primary Diene Interaction	Secondary Diene Interaction