Rep:Mod:Dorene

NH₃

General information

Information
Molecule name	Calculation method	Basic set	Final energy E(RB3LYP)	RMS gradient	Point group	N-H bond distance	H-N-H bond angle
NH₃	RB3LYP	6-31G(d,p)	-56,5577687299 a.u.	0.05399560 a.u.	C3V	1.01798Å	105.741

 Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

J mol of NH₃

test molecule

Media:YONGYINCHEN_PHUNT_NH3_OPTF_POP.LOG

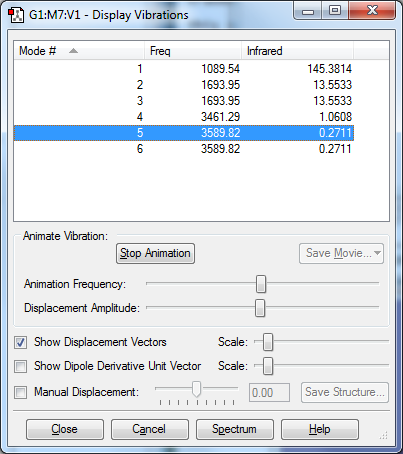
Vibration modes

 • 6 modes are expected from the 3N-6 rule. 
 • Modes 2&3 are degenerate to each other, so are modes 5&6. 
 • Modes 1,2,3 are bending vibrations and modes 4,5,6 are bond stretch vibrations. 
 • Mode 4 is highly symmetric,
 • Mode 1 is known as "umbrella" mode. 
 • As vibrations of modes 4,5,6 do not have a change in dipole moment, they are not IR active. Therefore 2 bands would be seen in experimental spectrum

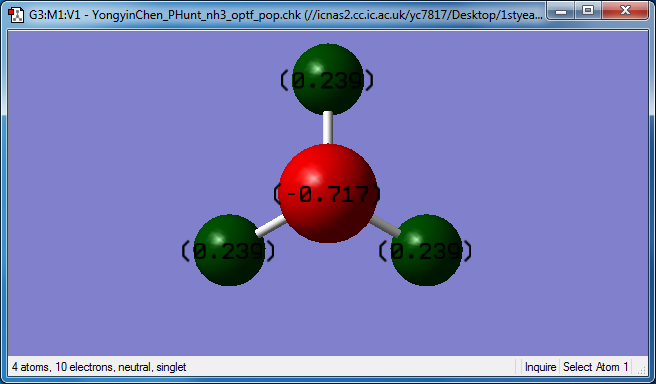
Charge of atoms

 • N is more electronegative than H.
 Therefore,
 • N is expected to have a negative charge of -0.717
 • H is expected to have a positive charge of +0.239

N₂

General information

Information
Molecule name	Calculation method	Basic set	Final energy E(RB3LYP)	RMS gradient	Point group	N-N bond distance	N-N structure
N₂	RB3LYP	6-31G(d,p)	-109.52412868 a.u.	0.00000365 a.u.	D*H	1.10550Å	Linear

Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000002     0.001800     YES
 RMS     Displacement     0.000003     0.001200     YES

J mol of N₂

test molecule

Media:YONGYINCHEN_PHUNT_N2_OPTF_POP.LOG

Vibration modes

 • N₂ has only one vibration mode which is bond stretch vibration.
 • No bands would appear in experimental spectrum.

Charge of atoms

 • N₂ has no charge on either of the atom as they are the same element and have same electronegativity.

H₂

General information

Information
Molecule name	Calculation method	Basic set	Final energy E(RB3LYP)	RMS gradient	Point group	H-H bond distance	H-H structure
H₂	RB3LYP	6-31G(d,p)	-1.17853936 a.u.	0.00000017 a.u.	D*H	0.74309Å	Linear

Item               Value     Threshold  Converged?
 Maximum Force            0.000211     0.000450     YES
 RMS     Force            0.000211     0.000300     YES
 Maximum Displacement     0.000278     0.001800     YES
 RMS     Displacement     0.000393     0.001200     YES

J mol of H₂

test molecule

Media:YONGYINCHEN_PHUNT_H2(2)_OPTF_POP.LOG

Vibration modes

 • Similar to N₂, H₂ has only one vibration mode which is bond stretch vibration as well.
 • No bands would be seen in experimental spectrum.

Charge of atoms

 • H₂ has no charge on either of the atom as they are the same element and have same electronegativity.

The Haber-Bosch process

Equation

 • N₂ + 3H₂ -> 2NH₃

Energy of the reaction

 • E(NH3)= -56.55776873 a.u.
 • 2*E(NH3)= -113.1155375 a.u.
 • E(N2)= -109.52412868 a.u.
 • E(H2)= -1.17853936 a.u.
 • 3*E(H2)= -3.53561808 a.u.
 • ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 a.u. = -146.48 kJ/mol
 • The energy of reaction is negative which indicates that this is an exothermic reaction and it actually is, therefore the product is more stable than the reactants.
 But the value obtained is quite different from the literature experimental value (-92 kJ/mol)^[1], because this value is calculated computationally.

CH₄

General information

Information
Molecule name	Calculation method	Basic set	Final energy E(RB3LYP)	RMS gradient	Point group	C-H bond distance	H-C-H bond angle
CH₄	RB3LYP	6-31G(d,p)	-40.44773109 a.u.	0.04153842 a.u.	TD	1.09194Å	109.471

 Item               Value     Threshold  Converged?
 Maximum Force            0.000044     0.000450     YES
 RMS     Force            0.000023     0.000300     YES
 Maximum Displacement     0.000124     0.001800     YES
 RMS     Displacement     0.000066     0.001200     YES

J mol of CH₄

test molecule

Media:YONGYINCHEN_PHUNT_CH4_OPTF_POP.LOG

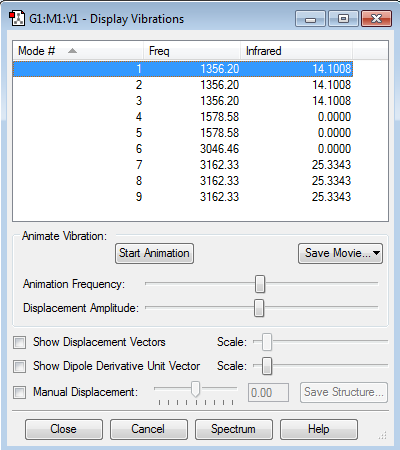
Vibration modes

 • 9 modes of vibrations would be expected. 
 • Modes 1&2&3 are degenerate to each other, so are modes 4&5 and modes 7&8&9. 
 • 2 kinds of vibration modes are present. Modes 1,2,3,4,5 are bending vibrations and modes 6,7,8,9 are bond stretch vibrations. 
 • Modes 4,5,6 is highly symmetric as the vibration of them do not produce dipole moment so they are IR inactive.
 • Therefore, 2 bands would be seen in the experimental spectrum of methane as expected.

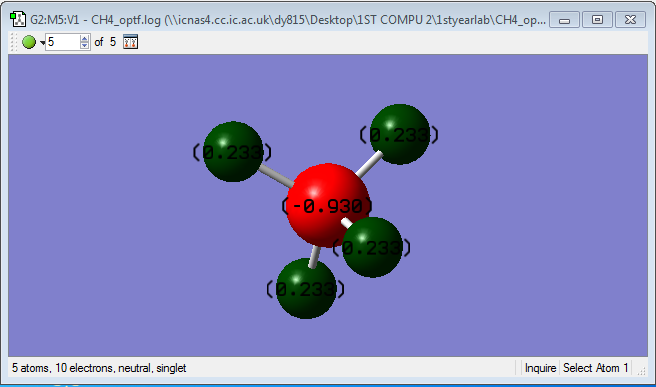
Charge of atoms

 • C is more electronegative than H.
 Therefore,
 • C is expected to have a negative charge of -0.930
 • H is expected to have a positive charge of +0.233

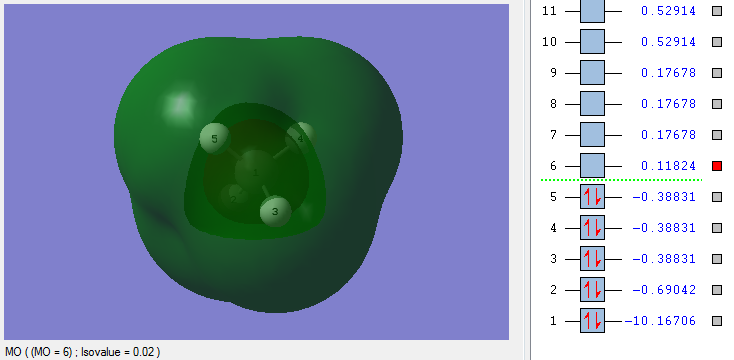
Molecular Orbitals (MO) of CH₄

MO diagram	Explanation
	• This MO is from two electrons of 1s atomic orbital(AO) from C-atom, electrons are delocalised only around C-atom, therefore it has the lowest energy (-10.16706 a.u.) and is a non-bonding orbital.
	• This occupied σ-bonding MO is the contribution from 2s AO of C-atom and 1s AO of H-atom, because it is symmetric, 1s AO of all 4 H-atoms are degenerate, so no specific H-atom is chosen to overlap. But as there is only one space available, 1s of a random H-atom among four is bonding.
	• The 3 occupied π-bonding MOs above are degenerate as they are the combination of three 2p AOs of C-atom and 1s AOs of the remaining three Hydrogen atoms. As shown, MO-5 is the highest occupied molecular orbital (HOMO) of CH₄.
	• This the σ-antibonding MO because the AOs are out of phase to each other. And as all electrons are used up to form one σ-bonding MO and three π-bonding MOs, it is unoccupied. Therefore, it is lowest unoccupied molecular orbital (LUMO) in this case.