Rep:Mod:Demonstrator:rs6817
Information about various molecules
This page documents the use of study and modelling of a series of molecules within the Gaussview software package.
NH3 molecule
The first studied molecule is NH3.
The information below is for an optimized NH3 molecule:
Method: B3LYP
Basis set: 6-31G(d.p)
Calculation: OPTF(optimise and frequency analysis)
Final energy: -56.5564054 a.u.
RMS Gradient Norm: 0.00980112 a.u.
Point Group: C3V
N-H bond length: 1.01798 Angstroms
H-N-H bond angle: 105.741 degrees
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000014 0.001800 YES
RMS Displacement 0.000009 0.001200 YES
Predicted change in Energy=-1.141690D-10
Optimization completed.
-- Stationary point found.
NH3 molecule |
Below is the file showing optimization of the NH3 molecule: Optimization link
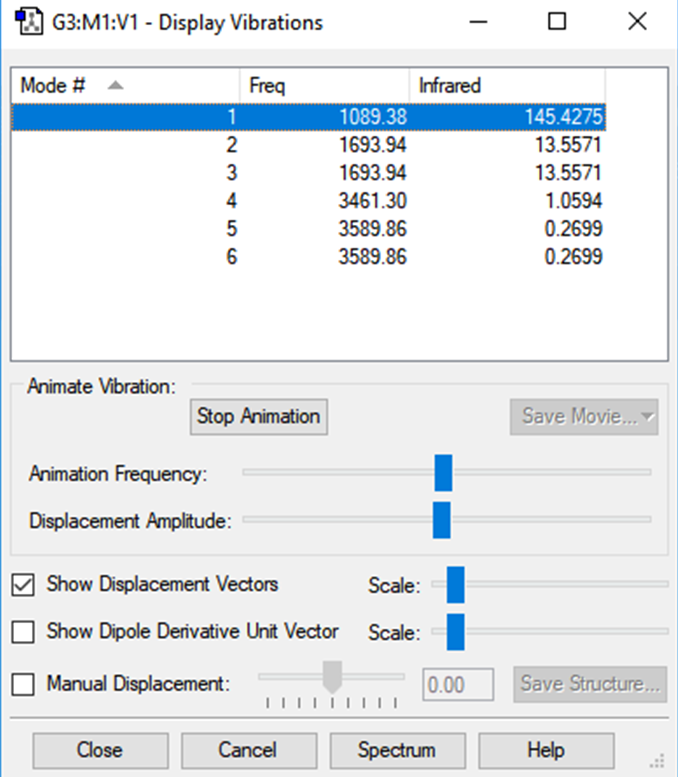
Following the 3N-6 (3*4)-6, as predicted there are 6 vibrations. Modes 2 and 3 & 5 and 6 are degenerate as they share the same energies. Mode 1, 2 and 3 are bedning vibrations whilst 4,5 and 6 are bond-stretch vibrations. Mode 4 is highly symmetric (potentially mode 1 too?). The umbrella mode is vibration 1 - as depicted by its behaviour. Based on this information, a gaseous Ammonia specturm should give 3 bands, 1 for mode 1, 1 for modes 2 and 3 together and modes 4,5 and 6 will likely fuse into a single band.
Here is the 'Display Vibrations' frame from Gaussview for an optimised NH3 molecule:
Below shows the relative charges of each atom in the ammonia molecule:
In terms of what would be expected for an N and H atom, N is more electronegative than H and so a negative charge accounts for the pulling of the less electronegative hydrogen atoms towards it.
N2 molecule
The second studied molecule is N2.
The information below is for an optimized N2, diatomic molecule:
Method: B3LYP
Basis set: 6-31G(d.p)
Calculation: OPTF(optimise and frequency analysis)
Final energy: -109.52412868 a.u.
RMS Gradient Norm: 0.00000060 a.u.
Point Group: D*H
N-N bond length: 1.10550 Angstroms
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400956D-13
Optimization completed.
-- Stationary point found.
The link to the optimisation file. Optimization link
N2 molecule |
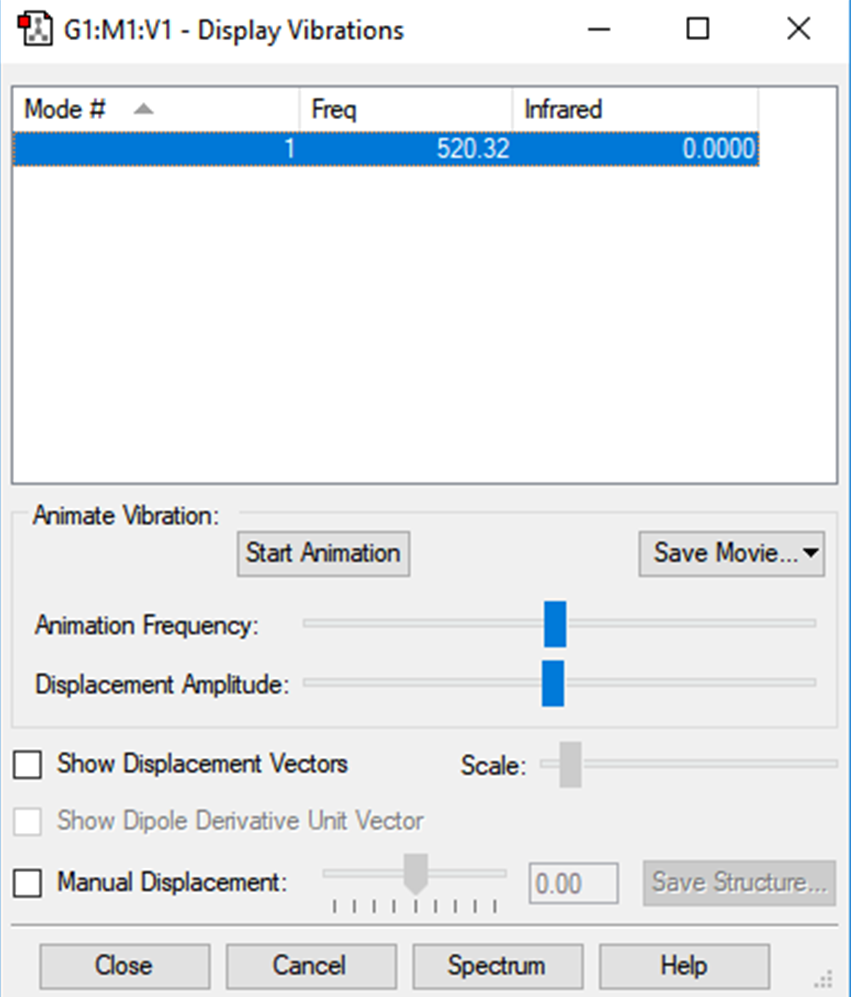
Vibrational analysis
There is no charge distribution across the N2 diatomic molecule. As both constituent atoms are the same, theyre electronegativities will cancel one another out.
H2 molecule
The third studied molecule is H2.
The information below is for an optimized N2, diatomic molecule:
Method: B3LYP
Basis set: 6-31G(d.p)
Calculation: OPTF(optimise and frequency analysis)
Final energy: -1.15928020 a.u.
RMS Gradient Norm: 0.09719500 a.u.
Point Group: D*H
N-N bond length: 0.6 Angstroms
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
The link to the optimisation file. Optimization link
H2 molecule |
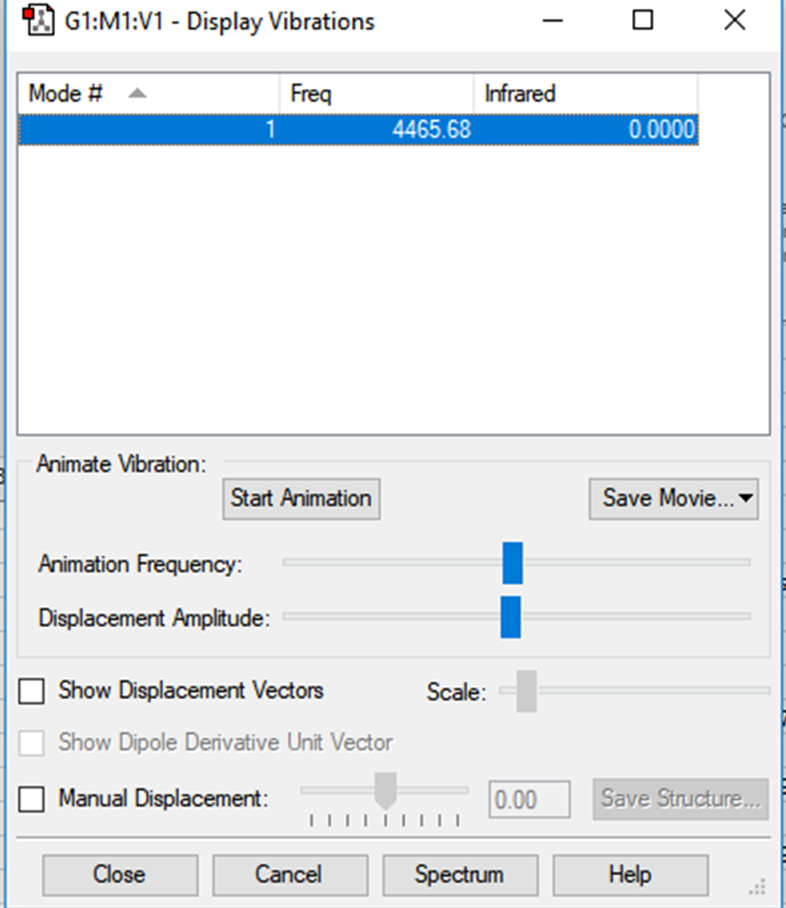
Vibrational analysis
There is no charge distribution across the H2 diatomic molecule. As both constituent atoms are the same, the electronegativities will cancel one another out.
CCSD Search
The CSD allows a search of metallic complexes. In co-ordinating N2, a Zinc based complex - NIFSON : catena-(bis(μ-2-methylimidazolato)-zinc dinitrogen)
Haber-Bosch process
The Haber-Bosch process converts N2(g) + H2(g) into NH3(g).
E(NH3)= -56.5564054 a.u. --> -148488.9 kj/mol-1 2*E(NH3)= -113.112908 a.u. --> -296970.3 kj/mol-1 E(N2)= -109.52412868 --> -287555.6 kj/mol-1 E(H2)= -1.15928020 --> -3043.7 kj/mol-1 3*E(H2)= -9131.1 kj/mol-1 ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -6371 kj/mol-1
To convert a.u. into Kj/mol-1 multiply by 2625.5.
The reaction is favoured in the direction of product formation, as there is a net negative energy difference, therefore the Ammonia product is more stable.
CL2 molecule
The molecule I decided to investigate is Cl2.
The information below is for an optimized Cl2, diatomic molecule:
Method: B3LYP
Basis set: 6-31G(d.p)
Calculation: OPTF(optimise and frequency analysis)
Final energy: -920.34853292 a.u.
RMS Gradient Norm: 0.01404387 a.u.
Point Group: D*H
N-N bond length: 1.98 Angstroms
Item Value Threshold Converged?
Maximum Force 0.000043 0.000450 YES
RMS Force 0.000043 0.000300 YES
Maximum Displacement 0.000121 0.001800 YES
RMS Displacement 0.000172 0.001200 YES
Predicted change in Energy=-5.277115D-09
Optimization completed.
-- Stationary point found.
The link to the optimisation file. Optimization link
Cl2 molecule |
Vibrational analysis
There is no charge distribution across the H2 diatomic molecule. As both constituent atoms are the same, their electronegativities will cancel one another out.
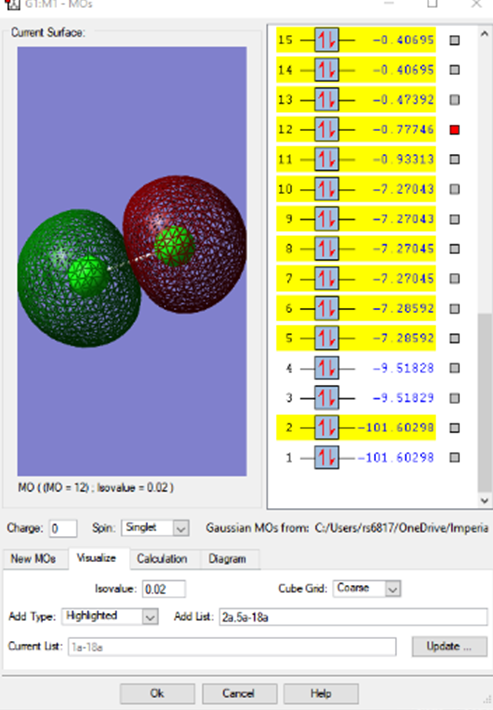
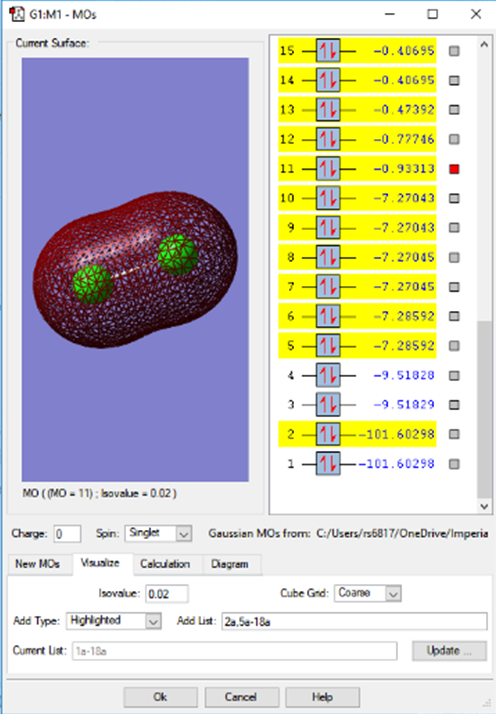
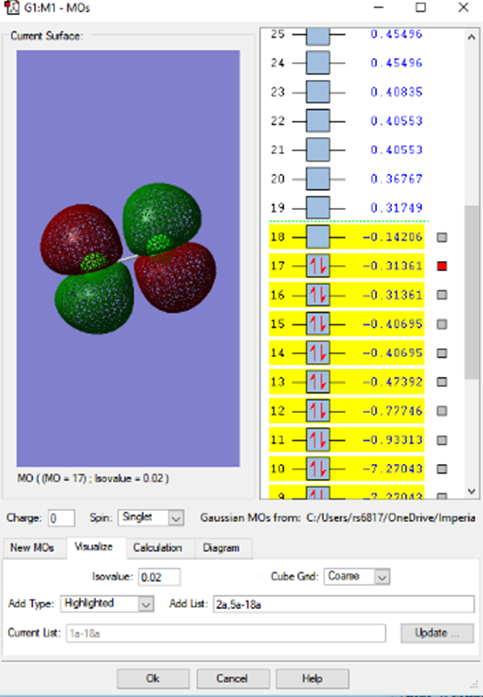
MO's of CL2 molecule
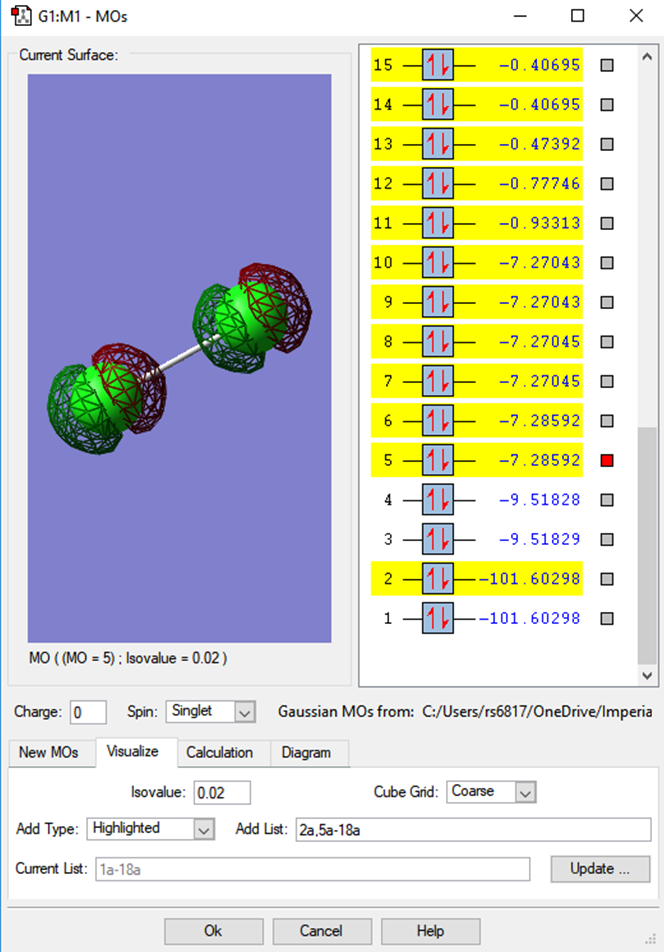
Below are some images of the MO's of the Cl2 diatomic.
The electron configuration of a chlorine atom is 1s2 2s2 2p6 3s2 3p5 , a total of 17 electrons, which in a diatomic will give 34 electrons to donate into the formed MO's.
2pz antibonding MO
The first observable MOs will show the difference between the bonding and antibonding orbitals. This MO is formed from 2 * 2pz atomic orbitals, organised along the z axis, across the bond. The energy of the orbitals allows them to interact and fuse, as shown in the bonding MO below. Both of these MOs are occupied.
2pz bonding MO
3s2 antibonding MO
When observing the same difference between the bonding and antibonding MO that is built from the 3s2 AOs, the difference in the probability density is observed. We can see the stark difference between the large AOs in the antibonding MO vs. the bonding form in the MO.
3s2 bonding MO
3py antibonding HOMO
The HOMO of chlorine is the antibonding form of the 3py AOs, it is difficult to determine if x or y due to the diatomic nature of the chlorine molecule. The energies of the MOs below show how close these all are in energy in the HOMO region.
In the upper HOMO region, antibonding MOs (formed from p AOs) are all full. An MO based analysis would suggest that the bond in the diatomic form of chlorine is therefore likely to easily dissociate, due to the contribution of the antibonding character.