Rep:Mod:DZC1990

Conformational analysis using Molecular Mechanics

In order to predict the most stable conformations of molecules and the reasons behind them, conformational analysis has been used. The possible observations in the experiments were explained by the use of 'molecular mechanics' and 'conformational analysis'. Energies calculated were also used to predict the expected conformers some molecules will take and explain the hyper stability seen in bridgehead olefins.

(I) Hydrogenation of Cyclopentadiene dimer

Cyclopentadiene molecules have a tendency to dimerise at room temperature via the Diels-Alder addition, a type of pericyclic reactions. Theoretically, there are two possible dimers that can be formed - exo (1) and endo (2) as shown below.

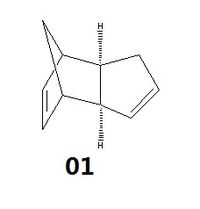
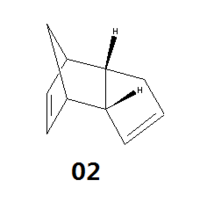
Figure 1.1: Cyclopentadiene dimers (1) and (2)

Intensive studies performed over the years have indicated that the cyclopentadiene molecules specifically dimerise to give only the endo dimer (2) at room temperature. In order to confirm and investigate this observation, various energies of the 2 dimers were calculated through computational modelling.

The calculated minimised energies of the dimers using the MMFF94(s) force-field option are given in Table 1.1:

Energies (kcal/mol)	Exo dimer (1)	Endo dimer (2)
Bond Stretching	3.54	3.47
Angle Bending	30.8	33.2
Stretch Bending	-2.04	-2.08
Torsional	-2.73	-2.95
Out-of-plane Bending	0.0149	0.0220
Van Der Waals	12.8	12.4
Electrostatic Interactions	13.0	14.2
Total	55.4	58.2

Table 1.1: Table comparing various minimised energies of exo dimer (1) and endo dimer (2)

Results shown in the table above indicate that the exo dimer (1) is given to be the thermodynamic product as it is more stable with a lower overall energy compared to the endo dimer (2). The biggest contribution comes from the angle bending energy, where the exdo dimer (1) has a lower energy by 2.4kcal/mol. Hence, the formation of the endo dimer (2) over the exo dimer (1) as reported in literature, despite the latter's greater stability, indicates that the Diels-Alder addition of cyclopentadiene molecules is of a kinetic control.

Various studies have been performed to explain this observation; looking at the transition states of the mechanisms in particular. Literature states that the transition state of the endo dimer (2) has an energy of 21.0 kcal/mol, which is 2.9kcal/mol lower in energy than the transition state of the exo dimer (1). As a result, the former transition state is quicker to form as it is more stable. The large number of endo dimer (2) transition state formed leads to the endo dimer (2) being preferentially formed at room temperature instead. Evidence of the exo dimer (1) formation requiring more energy to reach its transition state is further supported by the observation that heating the endo dimers to 180^oC-240^oC lead to the formation of some exo dimers. This was not observed at room temperature .

In addition, concerted cycloaddition reactions can only occur under specific selection rules. In the case of Diels-Alder cycloaddition of 2 cyclopentadiene molecules, the Huckel rule of _π4_s + _π2_s is followed. The mechanism requires the overlap of symmetrical frontier orbitals. By comparing the transition states of the exo dimer (1) and endo dimer (2), the positioning of the cyclopentadiene molecules directly above one another for the formation of the endo dimer (2) allows better overlap between the frontier orbitals. This results in a lowering of energy and greater stability in the transition state, hence explaining the energies found above.

Thus, it can be concluded that the cyclodimerisation of cyclopentadiene via Diels-Alder addition is kinetically controlled.

Upon hydrogenation, such as using a Pd catalyst/H₂ system, the endo dimer (2) forms either dihydro derivatives (3) or (4) as shown below.

Figure 1.2: Dihydo derivatives(3) and (4)

By comparing the minimised energies of the optimised geometries of dihydro derivatives (3) and (4), a prediction can be made on the relative ease of hydrogenation of endo dimer (2) to give either dihydro derivatives (3) and (4).

The calculated minimised energies of the dihydro derivatives using the MMFF94(s) force-field option are given in Table 1.2:

Energies (kcal/mol)	Dihydro derivative (3)	Dihydro derivative (4)	Energy differences (magnitude)
Bond Stretching	3.30	2.82	0.48
Angle Bending	30.9	24.7	6.2
Stretch Bending	-1.92	-1.65	0.27
Torsional	0.0535	-0.367	0.4205
Out-of-plane Bending	0.0138	0.0003	0.0135
Van Der Waals	13.3	10.6	2.7
Electrostatic Interactions	5.12	5.15	0.03
Total	50.7	41.3	9.4

Table 1.2: Table comparing various minimised energies of dihyro derivatives (3) and (4)

The thermodynamic stability of both dihydro derivatives can be determined by comparing their relative energies. Referring to Table 1.2, the differences in bond stretching, stretch bending, torsional, out-of-plane bending and electrostatic interactions energies are small and insignificant. It can be predicted that the higher stability of (4) is contributed by the angle bending energy and the Van Der Waal forces, which are 6.2kcal/mol and 2.7kcal/mol lower respectively in comparison to the energies of (3). From this, it can be determined that the angle strain highly affects the stability of the dihydro derivatives, which is expected as they are multi-rings compounds that have restricted conformations. In addition, the lower Van Der Waal forces seen in (4) indicated better intermolecular interactions, which help to lower the overall energy and stabilise the compound. Hence, formation of dihydro derivative (4) via hydrogenation of endo dimer (2) is expected to be easier and thermodynamically favoured.

Further hydrogenation will then produce the tetrahydro derivative shown below.

Figure 1.3: Tetrahydro derivative of cyclopentadiene dimer (2)

(II) Atropisomerism in an intermediate related to the synthesis of Taxol

Intermediates (9) and (10) shown below were proposed to be involved in the multi-steps synthesis of Taxol. Due to the restriction in rotation of bonds in the rings, particularly due to the presence of a double bond, both isomers can exist at room temperature, resulting in them being atropisomers. This is further supported by studies which have proven that addition across the alkene double bond, causing a change in sp² to sp³ geometric changes to the relevant carbon centers, result in faster conformational isomerisation. However, given sufficient time, one of the intermediates will eventually isomerise to the more stable intermediate. The more stable intermediate is found through comparing calculated energies of both isomers using the MMFF94s force field option, as shown below.

Energies (kcal/mol)	Taxol intermediate (9)	Taxol intermediate (9) parent hydrocarbon	Taxol intermediate (10)	Taxol intermediate (10) parent hydrocarbon
Structure
Jmol	Intermediate (9)	Intermediate (9)	Intermediate (9)	Intermediate (9)
Bond Stretching	7.67	6.97	7.54	6.77
Angle Bendng	28.4	32.2	18.7	24.5
Stretch Bending	-0.0533	0.329	-0.158	0.439
Torsional	0.132	9.41	0.284	8.14
Out-of-plane Bending	0.956	0.252	0.824	0.107
Van Der Waals	33.1	32.7	33.5	32.0
Electrostatic Interactions	0.307	0.000	-0.0573	0.000
Total	70.5	81.9	60.7	72.0

Table 1.3: Table comparing various minimised energies of taxol intermediates (9) and (10) and their parent hydrocarbons

Comparing the overall energies, it can be observed that taxol intermediate (10) is the more stable intermediate as it has ~11kcal/mol less energy than taxol intermediate (9). The biggest contribution comes from the angle bending energy, which is much higher for both the taxol intermediate (9) and its parent hydrocarbon when compared to taxol intermediate (10) and its parent hydrocarbon. This implies that the bending of the molecules, which then result in deviations from the expected angles (109.5^o for sp³ centers and 120^o for sp² centers), causes the most instability in the molecules.

Both intermediates are also observed to be highly unreactive in the functionalisation of the alkenes. Their hyperstable alkene characteristic can be explained by investigating the olefinic strain (OS) of the intermediates and their parent hydrocarbons. The olefin strain has been defined as the extra strain energy caused by the double bond in the bridgehead olefin when compared to its parent hydrocarbon. In order to calculate the OS values for both intermediates, the most stable conformers for both intermediates and their parent hydrocarbons were modeled and their energies were calculated and presented in Table 1.3. The OS values were obtained by finding the differences in torsional energies between an intermediate and its parent hydrocarbon. Since the only difference between the intermediates and their hydrocarbons is the alkene double bond in the ring, the OS value is directly related to the energies required for hydrogenation. To ensure fair comparison, all energies calculated were based on the one of the most stable conformers of each molecule, which is achieved by ensuring that the 6-membered ring is of a chair conformation. In addition, all 4 molecules were modeled to have identical chair conformation for the 6-membered ring.

From the calculations, intermediates (9) and (10) were noted to have significantly lower torsional energies than their parent hydrocarbons, resulting in calculated OS values of -9.28kcal/mol and -7.86kcal/mol respectively. Using the empirical rules formulated by Maier and Schleyer, intermediates (9) and (10) are categorised as isolable bridgehead olefins as their OS values are < 17kcal/mol. Hence, like all bridgehead olefins with such OS values, they are expected to be kinetically stable at room temperature, giving them their hyperstable alkene character.

References:

Spectroscopic Simulation using Quantum Mechanics

The NMR spectra of molecules can also be predicted by using Quantum Mechanics. These calculated results can then be compared with the chemical shifts reported in literature to investigate their accuracies.

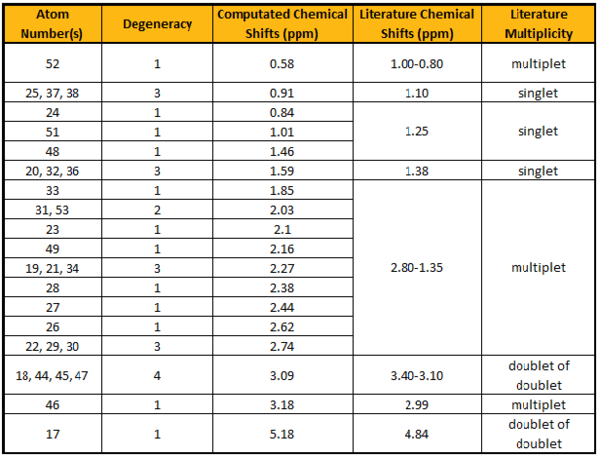
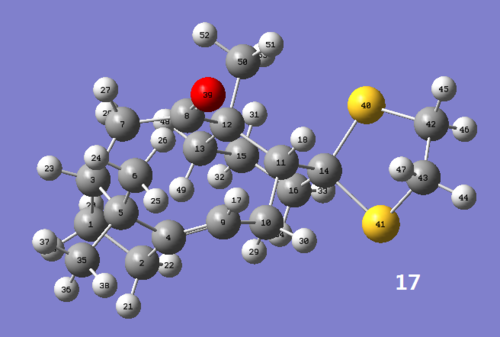
Molecule (17) is a derivative of taxol intermediate (9) found in the synthesis of Taxol. The ¹H and ¹³C NMR spectra were computed and analysed below.

Figure 2.1: Molecule (17)

Figure 2.2: ¹H NMR spectrum of molecule (17)

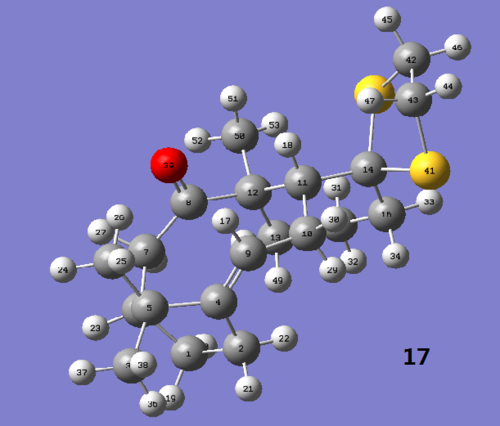
Figure 2.3: Labelled protons of molecule (17)

Table 2.1: Table illustrating the calculated shifts for ¹H NMR of molecule (17)

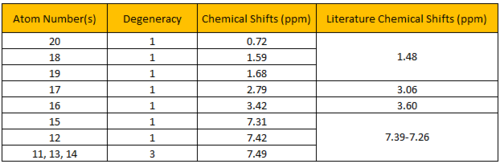
The chemical shifts in the ¹H NMR spectrum produced using Gaussian deviates from the literature by ~0.20-0.30 ppm, which is insignificant. An anomaly occurs for atoms #24, 48 and 51, which are expected to show a singlet in the NMR but are given their respective chemical shifts when computated. On close inspection of the respective protons, it was found that they were of different environments and should not have identical chemical shifts, implying an error in the reported results. In addition, the literature also poorly reported the peaks for atoms #19, 21-23, 26-31,33, 34, 49 and 51 as multiplets whereas they are given individual chemical shifts when computated. Given that the results were produced 23 years ago, where NMR techniques were not as advanced, such observation are expected. Hence the computed results are clearly more accurate.

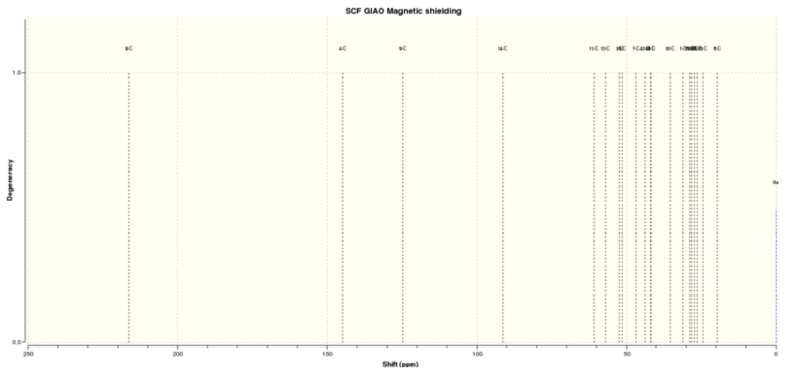
Figure 2.4: ¹³C NMR spectrum of molecule (17)

Figure 2.5: Labelled carbons of molecule (17)

<

Table 2.2: Table illustrating the calculated shifts for ¹³C NMR of molecule (17)

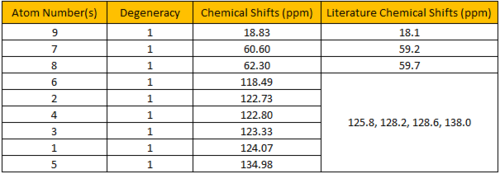
The chemical shifts in the ¹³C NMR spectrum produced using Gaussian are similar to the ones reported in the literature. The greatest deviation is observed for atom #14. This is because the Carbon atom is adjacent to 2 Sulfur atoms, which are considered to be heavy atoms, and correction to the chemical shift needs to be made to remove the spin-orbit coupling error.

The thermodynamic quantities of molecule (17) were also computed and listed below:

Types of energies	Energies(Hartree/Particle)
Zero-point correction	0.468397
Thermal correction to Energy	0.489751
Thermal correction to Enthalpy	0.490696
Thermal correction to Gibbs Free Energy	0.422010
Sum of electronic and zero-point Energies	-1651.414384
Sum of electronic and thermal Energies	-1651.393029
Sum of electronic and thermal Enthalpies	-1651.392085
Sum of electronic and thermal Free Energies	-1651.460770

Table 2.3: Thermodynamic quantities of molecule (17)

From Table 2.3, ΔG is calculated to be -1650kcal/mol. This value can be compared with the ΔG of molecule (18) to determine which molecule is more stable at room temperature.

References:

Analysis of the properties of the synthesised alkene epoxides

(I) Catalyst Structures
The stable precursor (21) of the Shi catalyst shown below was synthesised for the epoxidation of styrene and trans-B-methyltyrene.

Figure 3.1: Molecule 21 with labelled bond lengths and angles

Figure 3.2: Stick diagram of molecule 21 with the C-O bond lengths

Close examination of the C-O bond lengths in the anomeric centres with O-C-O substructures found that one C-O bond is significantly longer than the other. This is presented in Figure 3.2, where the bottom anomeric centre shows C-O bond lengths of 1.428Å and 1.456Å, when the expected bond length is 1.43Å. This is similarly found in the top anomeric structure. In addition, the terminal methyl groups are found to have shorter than normal C-C bonds (1.54Å) with values ranging from 1.500Å - 1.511Å. This observation is likely due to overlap of the p* orbitals in O atoms that have weak C-O bonds and the sp³ orbitals in C atoms. As a result the bonding orbitals of the C atoms are stabilised, resulting in stronger C-C bonds while the donation of some electron density to the p* orbital due to the overlap decreases the bond order and weakens the C-O bond. The O-C-O angles are also observed to be smaller than the expected value of 109.5^o. The anomeric centre that is contained in both the 5-membered ring and 6-membered ring has shorter than normal C-O bonds with values of 1.415Å and 1.423Å. The short C-O bond can be explained by the resonance effect to the nearby C=O group.

For the Jacobsen asymmetric catalyst, the stable pre-catalyst (23) formed in the reaction is shown below.

Figure 3.3: Molecule 23

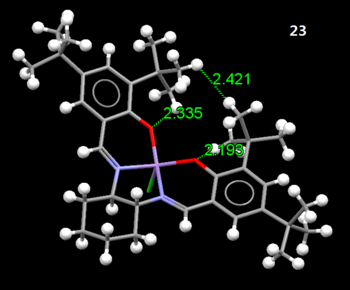
Figure 3.4: Sticks and ball diagram of molecule 23

Referring to Figure 3.4, a close approach of the 2 adjacent t-butyl groups on the rings is observed. When the shortest distance between the protons were measured, it was found to be 2.421Å, which corresponds to the Van Der Waals radii for the maximum attractive interaction. This helps to stabilise the molecule strongly. The dominance of the strong H...H Van Der Waals interactions is further supported by the fact that it is present despite the close proximity that results in repulsive O..H Van der Waals interactions (2.335Å and 2.193Å) being observed too.

The rest of the report will be based on the (R) and (S) styrene oxides and the (R)(R), (S)(S), (R)(S), (S)(R) trans-ß-Methylstyrene oxides.

(II) NMR of selected epoxides
The NMR spectra of the selected epoxides were computed and the calculated chemical shifts were compared with those found in literature as no NMR spectra of the epoxides were produced in the actual synthesis.

(R)-Styrene oxide
The (S)-Styrene oxide produces the same NMR data as the (R)-Styrene oxide and will not be shown below.

Figure 4.1: Labelled atoms of (R)-Styrene oxide

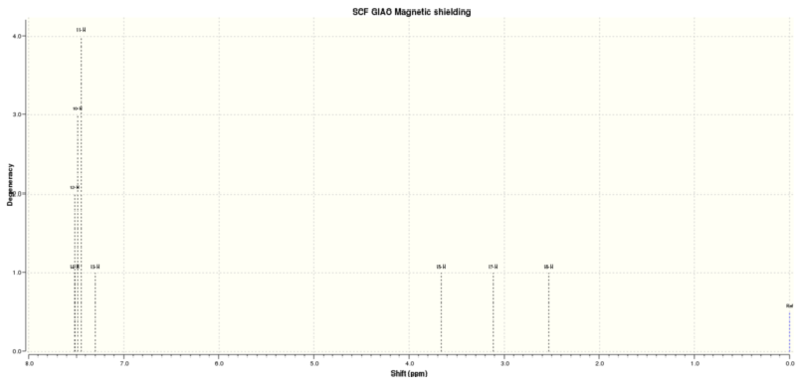
Figure 4.2: ¹H NMR spectrum of (R)-Styrene oxide

Table 3.1: Table illustrating the calculated shifts for ¹H NMR of (R)-Styrene oxide

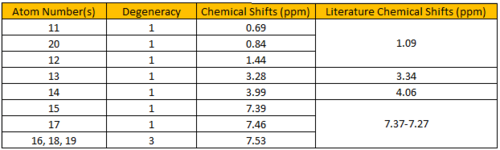
The calculated ¹H NMR chemical shifts are in line with the reported values with insignificant derivations of <0.20ppm. Precision is seen in the calculated values which indicates that proton #13 has a different chemical shift than the rest of the protons. This is likely due to the close proximity of proton #13 with the O atom. However, protons #11 and #14 should not have the same chemical shift as protons #10 and #12 as they are not chemically equivalent.

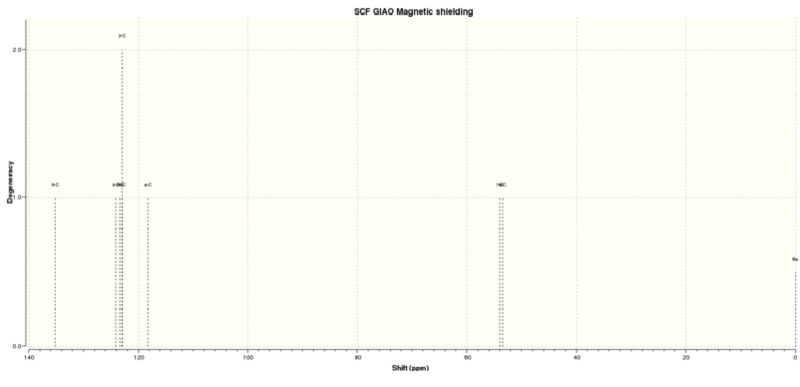
Figure 4.3: ¹³C NMR spectrum of (R)-Styrene oxide

Table 3.2: Table illustrating the calculated shifts for ¹³C NMR of (R)-Styrene oxide

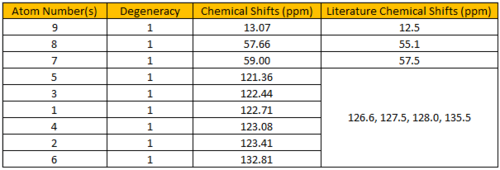
The calculated ¹³C NMR chemical shifts are in line with the reported values with insignificant derivations of <5.00ppm. The literature failed to report 2 of the chemical shifts for the protons, likely due to its close proximity on the spectra that results in overlaps.

(R),(R)-trans-ß-Methylstyrene oxide
The (S),(S)-trans-ß-Methylstyrene oxide produces the same NMR data as the (R),(R)-trans-ß-Methylstyrene oxide and will not be shown below.

Figure 4.4: Labelled atoms of (R),(R)-trans-ß-Methylstyrene oxide

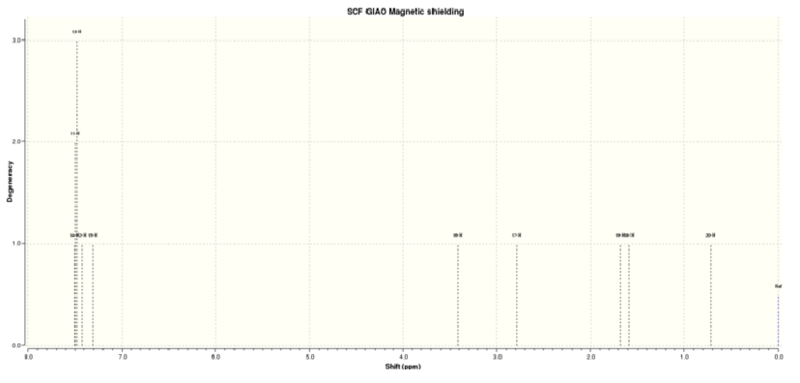
Figure 4.5: ¹H NMR spectrum of (R),(R)-trans-ß-Methylstyrene oxide

Table 3.3: Table illustrating the calculated shifts for ¹H NMR of (R),(R)-trans-ß-Methylstyrene oxide

The calculated ¹H NMR chemical shifts are in line with the reported values. Protons #18-20 were reported to have 3 different chemical shifts despite belonging to a -CH₃ group. This indicates that the computed results took into account that presence of slow rotation about the C atom due to the hindrance of the O atom which results in the 3 protons being seen as having different environments. Additionally, the aromatic proton #15 does not have the same chemical shift as proton #14 despite being in the same chemical environment. This implies that they are magnetically inequivalent. This is possible if there's slow rotation about the C(Ph)-C(OC) bond.

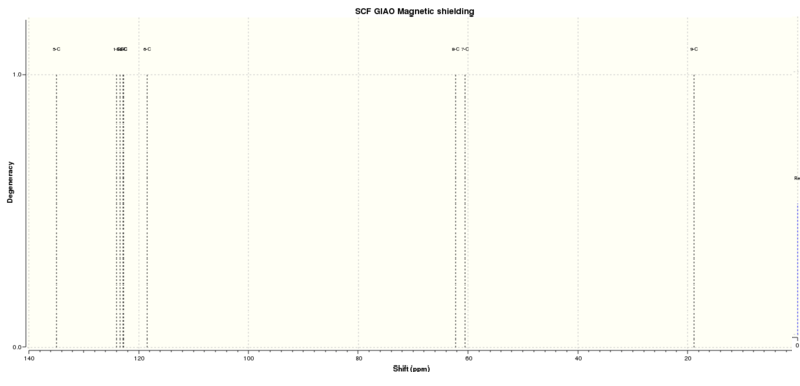
Figure 4.6: ¹³C NMR spectrum of (R),(R)-trans-ß-Methylstyrene oxide

Table 3.4: Table illustrating the calculated shifts for ¹³C NMR of (R),(R)-trans-ß-Methylstyrene oxide

The calculated ¹³C NMR chemical shifts are in line with the reported values. As seen previously, the computed results show individual chemical shifts for the aromatic carbons which is not seen in the literature.

(R),(S)-trans-ß-Methylstyrene oxide
The (S),(R)-trans-ß-Methylstyrene oxide produces the same NMR data as the (R),(S)-trans-ß-Methylstyrene oxide and will not be shown below.

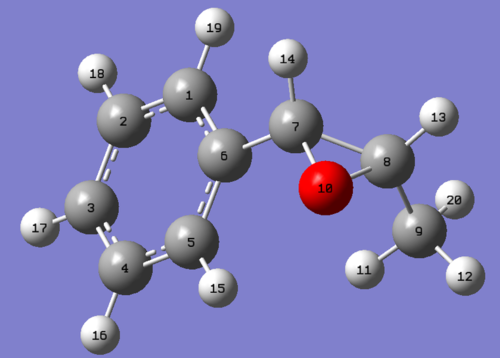
Figure 4.7: Labelled atoms of (R),(S)-trans-ß-Methylstyrene oxide

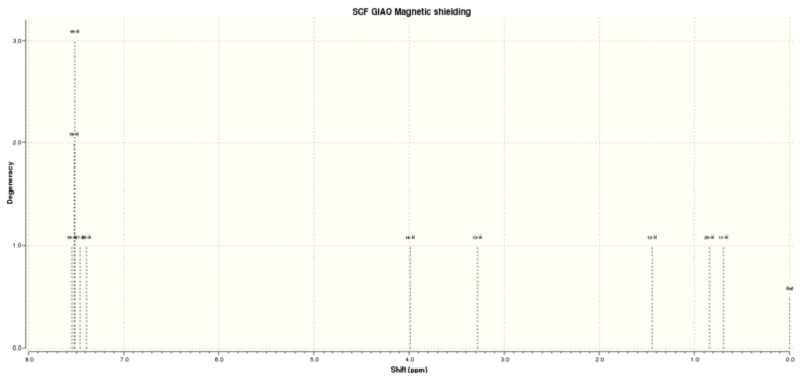
Figure 4.8: ¹H NMR spectrum of (R),(S)-trans-ß-Methylstyrene oxide

Table 3.5: Table illustrating the calculated shifts for ¹H NMR of (R),(S)-trans-ß-Methylstyrene oxide

The calculated ¹H NMR chemical shifts are in line with the reported values. The observation for (R),(R)-trans-ß-Methylstyrene oxide is also seen here; protons #11, 12 and 20 are found to be of different chemical shifts despite belonging to the same -CH₃ group. Similarly, protons #15 and 19 are calculated to have different chemical shifts despite being chemically equivalent, implying that they are magnetically inequivalent.

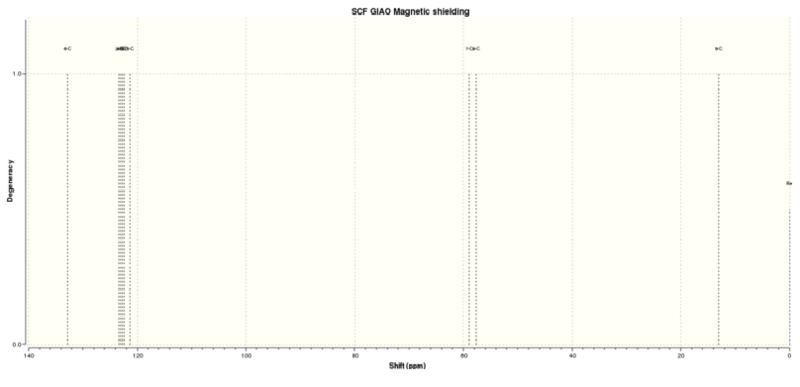
Figure 4.9: ¹³C NMR spectrum of (R),(S)-trans-ß-Methylstyrene oxide

Table 3.6: Table illustrating the calculated shifts for ¹³C NMR of (R),(S)-trans-ß-Methylstyrene oxide

The calculated ¹³C NMR chemical shifts are in line with the reported values. As seen previously, the computed results show individual chemical shifts for the aromatic carbons which is not seen in the literature.

(III) Calculated chiroptical properties of selected epoxides

The optical rotation values were calculated for 3 different epoxides; their respective enantiomers were assumed to have the same values but of different signs. No comparison is made with experimental results as none were produced due to the lack of time, hence comparison is made with litera

Epoxides	Calculated values of [α]D (o)	Reported values of [α]D (o)
(R)-Styrene Oxide	-179.79	-23.7
(R),(R)-trans-ß-Methylstyrene oxide	+131.77	+44.3
(S),(R)-trans-ß-Methylstyrene oxide	+33.99	+38.6

Table 4.1: Table showing the epoxides and their calculated optical rotations

The calculated values of [α]_D (^o) all show the same sign as the ones reported. However, the computed value for (R)-Styrene oxide largely deviates from the literature value, with a difference of 157^o. Similarly, the computed value for (R),(R)-trans-ß-Methylstyrene oxide also deviates from the literature by 87^o. Only the computed value for (S),(R)-trans-ß-Methylstyrene oxide is close to the value reported. Since the specific optical rotation already takes into account the path length and the concentration of the molecules, the large deviation is likely due to the difference in conformations between the ones used for calculations and the ones done in experiment. This is because the computed values differ for different conformers of the same compound. At the same time, it is also possible that the deviation is due to presence of impurities during measurement in the experiment. This is because the epoxides are produced in a racemic mixture and separation is required before measuring the optical rotation. Hence it is difficult to evaluate the accuracy of the computed results and the literature results as different literature reports produce different values too. One way of improving the computed results will be to repeatedly produce optimised molecules for computation.

(IV) Using the properties of transition state for the reaction
Shi catalyst transition states
Trans-ß-Methylstyrene oxide and styrene oxide were chosen for this segment.

Out of the 8 transition states provided for the (R),(R)-trans-ß-Methylstyrene oxide and the (S),(S)-trans-ß-Methylstyrene oxide, the ones with the lowest energies, i.e. largest magnitude since G<0, were chosen for further calculations. This is because the lowest energies transition states are the most stable and will most likely occur to give the epoxides. The values obtained from the .log files were also converted from Hartree/particle to Joules/mol.

G of (R),(R)-trans-ß-Methylstyrene oxide (Hartree/Particle)	-1343.032443
G of (S),(S)-trans-ß-Methylstyrene oxide (Hartree/Particle)	-1343.024742
G of (R),(R)-trans-ß-Methylstyrene oxide (Joules/mol)	-3.5261343E+09
G of (S),(S)-trans-ß-Methylstyrene oxide (Joules/mol)	-3.5261341E+09
∆G (Joules/mol)	-2.02E+04
K ([(R),(R) enatiomer]/[(S),(S) enantiomer])	3485.09
Ratio of (R),(R)-trans-ß-Methylstyrene oxide	0.9997
Ratio of (S),(S)-trans-ß-Methylstyrene oxide	2.869E-04
Enantiomeric excess (%)	99.9
Reported enantiomeric excess (%)	96-98

Table 5.1: Table showing calculations for the transition states for the epoxidation of trans-ß-Methylstyrene

The difference in free energies (∆G) is calculated to be -2.02E+04 Joules/mol, implying that (R),(R)-trans-ß-Methylstyrene oxide has a more stable transition state. Given that ∆G =-RTlnK, where R is the gas constant(8.314JK^-1mo^-1) and T is the temperature(298.15K). The ratio of concentrations of (R),(R)-trans-ß-Methylstyrene oxide over (S),(S)-trans-ß-Methylstyrene oxide is denoted as K and given to be 3485.09. Since the ratio of both concentrations add up to 1, the predicted enantiomer excess is calculated to be 99.9% with the (R),(R)-trans-ß-Methylstyrene oxide being the dominating enantiomer. This is in line with the reported value of 96-98% by Shi

G of (R)-styrene oxide (Hartree/Particle)	-1303.738044
G of (S)-styrene oxide (Hartree/Particle)	-1303.738503
G of (R)-styrene oxide (Joules/mol)	-3.422967E+09
G of (S)-styrene oxide (Joules/mol)	-3.422968E+09
∆G (Joules/mol)	1.21E+04
K ([(R) enantiomer]/[(S) enatiomer])	0.615
Ratio of (R)-styrene oxide	0.619
Ratio of (S)-styrene oxide	0.381
Enantiomeric excess (%)	23.8
Reported enantiomeric excess (%)	24.3

Table 5.2: Table showing calculations for the transition states for the epoxidation of styrene

The difference in free energies (∆G) is calculated to be 1.21E+04 Joules/mol, implying that (S)-styrene oxide has a more stable transition state. Given that ∆G =-RTlnK, where R is the gas constant(8.314JK^-1mo^-1) and T is the temperature(298.15K). The ratio of concentrations of (R)-styrene oxide over (S)-styrene oxide is denoted as K and given to be 0.615. The predicted enantiomer excess is calculated to be 23.8% with the (R)-styrene oxide being the dominating enantiomer. This is also in line with the reported value of 24.3% by Shi.

Jacobsen catalyst transition states

G of (S),(R)-cis-ß-Methylstyrene oxide (Hartree/Particle)	-3383.259559
G of (R),(S)-cis-ß-Methylstyrene oxide (Hartree/Particle)	-3383.25106
G of (S),(R)-cis-ß-Methylstyrene oxide (Joules/mol)	-8.88275E+09
G of (R),(S)-cis-ß-Methylstyrene oxide (Joules/mol)	-8.88273E+09
∆G (Joules/mol)	-2.23E+04
K ([(S),(R)enantiomer]/[(R),(S) enantiomer])	8114.63
Ratio of (S),(R)-cis-ß-Methylstyrene oxide	1.23E-04
Ratio of (R),(S)-cis-ß-Methylstyrene oxide	0.9999
Enantiomeric excess (%)	99.9%
Reported enantiomeric excess (%)	92

Table 5.3: Table showing calculations for the transition states for the epoxidation of cis-ß-Methylstyrene

The difference in free energies (∆G) is calculated to be -2.23E+04 Joules/mol, implying that (S),(R)-cis-ß-Methylstyrene oxide has a more stable transition state. Given that ∆G =-RTlnK, where R is the gas constant(8.314JK^-1mo^-1) and T is the temperature(298.15K). The ratio of concentrations of (S),(R)-cis-ß-Methylstyrene oxide over (R),(S)-cis-ß-Methylstyrene oxide is denoted as K and given to be 8114.63. The predicted enantiomer excess is calculated to be 99.9% with the (R),(S)-cis-ß-Methylstyrene oxide being the dominating enantiomer. This is slightly higher than the experimental results by Jacobsen but it still ties in with the observation that the (R),(S)-cis-ß-Methylstyrene oxide is preferentially formed.

G of (S),(S)-trans-ß-Methylstyrene oxide (Hartree/Particle)	-3383.262481
G of (R),(R)-trans-ß-Methylstyrene oxide (Hartree/Particle)	-3383.254344
G of (S),(S)-trans-ß-Methylstyrene oxide (Joules/mol)	-8.88276E+09
G of (R),(R)-trans-ß-Methylstyrene oxide (Joules/mol)	-8.88274E+09
∆G (Joules/mol)	-2.14E+04
K ([(S),(S)enantiomer]/[(R),(R) enantiomer])	5530.45
Ratio of (S),(S)-trans-ß-Methylstyrene oxide	0.9998
Ratio of (R),(R)-trans-ß-Methylstyrene oxide	1.81E-04
Enantiomeric excess (%)	99.96
Reported enantiomeric excess (%)	92

Table 5.4: Table showing calculations for the transition states for the epoxidation of trans-ß-Methylstyrene

The difference in free energies (∆G) is calculated to be -2.14E+04 Joules/mol, implying that S),(S)-trans-ß-Methylstyrene oxide has a more stable transition state. Given that ∆G =-RTlnK, where R is the gas constant(8.314JK^-1mo^-1) and T is the temperature(298.15K). The ratio of concentrations of S),(S)-trans-ß-Methylstyrene oxide over (R),(R)-trans-ß-Methylstyrene oxide is denoted as K and given to be 5530.45. The predicted enantiomer excess is calculated to be 99.96% with the (S),(S)-trans-ß-Methylstyrene oxide being the dominating enantiomer. This is slightly higher than the literature value of 92% but the preference for the formation of (S),(S)-trans-ß-Methylstyrene oxide is supported.

(V) Investigating the non-covalent interactions in the active-site of the reaction transition state
The (R),(R)-trans-ß-Methylstyrene oxide transition state using the Shi catalyst is chosen for this analysis.

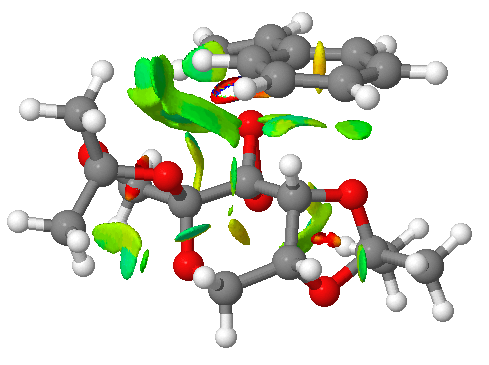
Figure 5.1: NCI analysis of the transition state using Shi catalyst to form (R),(R)-trans-ß-Methylstyrene oxide

It can be observed that active site in the Shi catalyst is positioned at one of the dioixirane O atoms. Observation of blue and green electron density near the active site indicates very attractive interaction between the catalyst and the alkene at this position. Specifically, the 5-membered ring on the Shi catalyst shows strong interaction with the protons on the methyl group and the phenyl ring which are positioned closely to the alkene functional group such that they enclose it. In addition, the dioxirane O atom that is not involved in the epoxidation shows hydrogen bond like interaction with a proton on the protruding methyl group at the other end. Intramolecular hydrogen bonding interaction is also observed in the Shi catalyst between the proton on the methyl group and ether O in the 6-membered ring. These attractive interactions help to stabilise the overall system and are a result of an endo-type interaction between the dioxirane O atom and the alkene functional group where the latter is positioned directly above the former. As a result, the epoxidation of the trans-ß-Methylstyrene is a syn addition to the alkene double bond. This explains the formation of the (R),(R)-trans-ß-Methylstyrene oxide enantiomer from this transition state.

(VI) Investigating the Electronic topology (QTAIM) in the active-site of the reaction transition state
The electronic topology of the transition state for the formation of (R),(R)-trans-ß-Methylstyrene oxide using Shi catalyst is shown below.

Figure 6.1: Electronic topology of the transition state using Shi catalyst to form (R),(R)-trans-ß-Methylstyrene oxide

Atoms that are involved in weak non-covalent bond critical point(BCP) are annotated in Figure 6.1. On close inspection, it is observed that there is an absence of a bond (i.e. BCP not seen) between the dioxirane O atoms in the Shi catalyst. With the lack of a covalent bond, the O atom that is not involved in the epoxidation is stabilised by hydrogen bonding with a proton on the methyl group as it has the most suitable distance for attractive interaction. On the other hand, the O atom involved in epoxidation is stabilised by weak non-covalent interactions with the C atom on the alkene C=C that is less hindered. This illustrates the means of epoxidation. In additional, the overall structure is stablised by favourable weak interactions such as hydrogen bonding between the O atom in the 5-membered ring with suitable H atoms and H...H Van Der Waals interactions.

(VII) Suggesting new candidates for investigations
One alkene that can be epoxidised to give an epoxide with [α]_D=835.9^o is (+)-pulegone shown below:

Figure 7.1: Epoxidation of (+)-pulegone

This will give cis R-(+)-pulegone oxide.

Conclusion
In conclusion, the use of computational methods has allowed an expansion on the experiment performed for the epoxidation of selected alkenes using Shi catalyst and Jacobsen catalyst. It has proven useful in conformational analysis of specific compounds to explain unexpected observations seen in experiments. Similarly, it also allows the computation of NMR spectra of various optimised molecules which can then be compared with the ones produced in literature. More importantly, it helps to calculate free energies which is use to identify the stability of the molecules. Optical rotation of chiral epoxides were also computed but more can be expanded in this area to ensure its accuracy. Computational methods also allow close inspection of active sites in catalyst during the transition state in order to understand the mechanism behind it. It has certainly proven useful in explaining and understanding the accuracy of data collected.

References: