Module 3: Transition States

Introduction

Through the use of GaussView 5.0, energies and transition states of different molecules were analysed. Different optimisation methods and basis sets were used, each with their own advantages and disadvantages. Starting with the Cope rearrangment, a pericyclic reaction consisting of a [3,3]-sigmatropic shift in 1,5-hexadiene. The rearrangement can be considered to go via a transition state, energetically and structurally equivalent to a diradical due to the absence of charge although, it is widely accepted that the reaction occurs through a concerted mechanism.

The Cope rearrangement can occur via a "chair" or "boat" conformation. It will be computationally determined which is the lower energy conformation. Both gauche and anti conformations of 1,5 hexadiene will be used in the experiment. The difference between the gauche and anti conformations is the dihedral angle which affects orbital orientations and hence orbital overlap. The gauche conformation tends to give unfavourable steric clashes due to long chains.

Nf710 (talk) 10:15, 21 April 2016 (BST) It would have been good here if you could have shown some understanding of the methods.

Optimisation of the Cope Rearrangement

Optimizing Reactants and products

Anti Linkage

Using GaussView 5.0, an anti conformation of 1,5 hexadiene was drawn and cleaned. The anti conformation is anti periplanar, so the dihedral angle was changed to 180°. The structure was optimised at the HF/3-21G level. The hartree fock method uses a single slater determinant to evaluate the wave function of the system. ^[1]It is a fast basis set, ideal for simple systems providing vague energies and geometries expected, not the exact experimental value.^[2] Using the "Symmetrize" function, the point group of this conformer was determined.

Nf710 (talk) 10:17, 21 April 2016 (BST) the method is not related to the basis set.

Table 1: Summary of Anti conformer
Structure	Results Summary	Point Group	Energy (hartrees)
		C_2h	-231.68907067

Gauche Linkage

The same process is carried out as in the previous section however, the dihedral angle in this case is 60°.

Structure	Results Summary	Point Group	energy (hartrees)
		C₂	-231.68771610

In the specific conformers shown above, it is seen that the gauche conformer is lower in energy than the anti however, this is not the case for all anti conformers. Due to secondary orbital interactions, gauche conformers are usually higher in energy than anti. These interactions can be seen in the HOMO of the gauche conformer but not in the anti conformer (both shown below).

HOMO of Gauche3 conformer showing strong bonding interaction

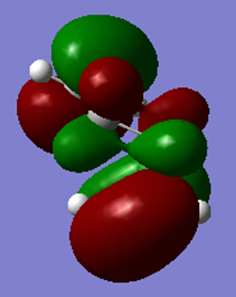
Optimization of gauche3 conformer

Gauche3 is the lowest energy conformer due to favourable orbital overlap, which cause a stabilizing effect which outweighs the steric repulsion. If the bulk around this conformer was increased, it is possible that this conformation would be less favourable as steric factors outweigh the stabilization energy experienced from orbital overlap.

Nf710 (talk) 10:18, 21 April 2016 (BST) Good understanding of the ordering of conformers

Structure	Results Summary	Point Group	Energy (hartrees)
		C₁	-231.69266120

Optimization and reoptimization of anti 2 conformer

Structure	Results Summary	Point Group	Energy (hartrees)
		C_i	-231.69253528

The anti2 conformer was optimized, using the HF\3-21G method, to a minimum. The total energy from Appendix 1 is -231.69254. This is lower than that calculated due to small discrepancies in bond angles. It is also possible that there is no discrepancy due to rounding.

Structure	Results Summary	Point Group	Energy (hartrees)
		C_i	-234.61171061

The reoptimization was completed using the B3LYP/6-31G* method. this method uses density functions of electrons to account for repulsion when determining energy. The result of this is that the outcome is closer to experimental values than that seen using the HF/3-21G method. For this reason, there is a change in geometry. Due to different approximations being applied and varying zero-point energies, the energy cannot be compared.^[3]

Nf710 (talk) 10:21, 21 April 2016 (BST) Basic understanding, could have gone into more detail

list of vibrations for reoptimized anti2 conformer

Atom	HF/3-21G	B3YLP/6-31G*
C1-C4	1.31613	1.33349
C4-C6	1.50891	1.50423
C6-C9	1.55275	1.54811

As seen in the table above, C1-C4 increases in bond length using DFT, where as, C4-C6 and C6-C9 decrease. The bond lengths from the DFT optimization is comparable to literature values.

Atoms	HF/3-21G (°)	B3YLP/6-31G* (°)
C1-C4-C5-C9	114.66880	118.57128
C4-C5-C9-C12	-180.00000	-180.00000
C5-C9-C12-C14	-114.66880	-11857128

As the table shows, there is an increase in the dihedral angle of approximately 4°.

The frequency calculations show absence of negative vibrational frequencies. This indicated all vibrational frequencies are real and that the critical point is a minimum in this case.

Sum of electronic and zero-point Energies= -234.469215

Sum of electronic and thermal Energies= -234.461866

Sum of electronic and thermal Enthalpies= -234.460922

Sum of electronic and thermal Free Energies= -234.500803

The first of these is the potential energy at 0 K including the zero-point vibrational energy (E = E_elec + ZPE), the second is the energy at 298.15 K and 1 atm of pressure which includes contributions from the translational, rotational, and vibrational energy modes at this temperature (E = E + E_vib + E_rot + E_trans), the third contains an additional correction for RT (H = E + RT) which is particularly important when looking at dissociation reactions, and the last includes the entropic contribution to the free energy (G = H - TS).

The frequencies which are obtained are calculated through the second derivates of energy which is a force constant for that degree of freedom. This is used to obtain the vibrational frequency from the vibronic harmonic oscillator equation. A negative k value would therefore result in an imaginary frequency.^[4]

Optimizing the "Chair" and "Boat" Transition Structures

3 different methods have been used to optimise the chair and boat transition structures through the HF/3-21G level of theory.

Optimizing the allyl fragment (CH₂CHCH₂)

Structure	Results Summary	Point Group	energy (hartrees)
		C_2v	-115.82304010

Optimization to a Transition State

The allyl fragment was duplicated and optimized to a chair transition state. The calculation set up was an "optimization and frequency", with optimization to a "TS(Berny)". Force constant was set to calculate once. "Opt=NoEigen" was an added parameter which stops the calculation crashing if more than one imaginary frequency is detected during the optimization which can often happen if the guess transition structure is not good enough.

Structure	Results Summary	Energy
		-231.61932235

An inter-fragment distance was set at 2.2 Å and the resultant distance was 2.02041 Å. An imaginary frequency was observed at -817.87 cm^-1. This shows the breaking and forming of bonds at the transition state allowing the determination of whether a transition state has been achieved.

Optimization using Frozen Coordinate Method

The Redundant Coord Editor was used to freeze terminal carbons. This optimizes remaining carbons so that once unfrozen, only inter-fragment bond distance needs to be optimized. This was optimized at HF/3-21G level of theory. The molecule was then optimized to change frozen bonds. The inter-fragment distance was set at 2.2 Å and the output had a distance of 2.02060 Å. Analysis of the LOG file showed one imaginary frequency at -817.91 cm^-1 confirming a transition state has been achieved.

Structure	Results Summary	Energy (hartrees)
		-231.61483163

Both TS(Berny) and frozen coordinates method resulted in negative frequencies being obtained.

Atom	TS(Berny) (Å)	frozen coordinate method (Å)
C6-C11	2.02051	2.02056
C3-C14	2.02049	2.02060

The table shows a difference in inter-fragment distance between terminal carbon atoms. These distances are very similar so for a simple molecule such as this, both methods seem to work well.

Optimizing the boat conformer

In this optimization, the QST2 method was used. The benefit of this method is that the transition state is automatically generated by providing the reactant and product. The anti2 confromer was used. This was sopied into a new window as a reactant and reorganized into the product. The atoms for both structures were labelled the same to ensure Gaussian is able to interpolate between them. The initial run failed as the molecule was not rotated around the central bonds. For this reason, the central dihedral angle for both product and reactant was modified to 0° and the inside C-C-C angles were modified to 100°. QST2 was run again.

Reactant and product conformers of Anti2

Boat Reactant and product conformers of Anti2

Structure	Results Summary	Energy (hartrees)
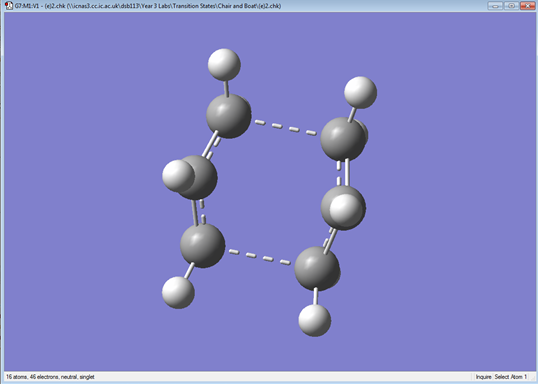
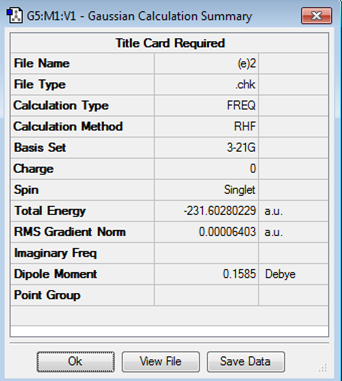
		-231.60280229

An imaginary frequency was observed at -839.99 cm^-1 confirming that a transition state has been reached. the vibration of this is shown below.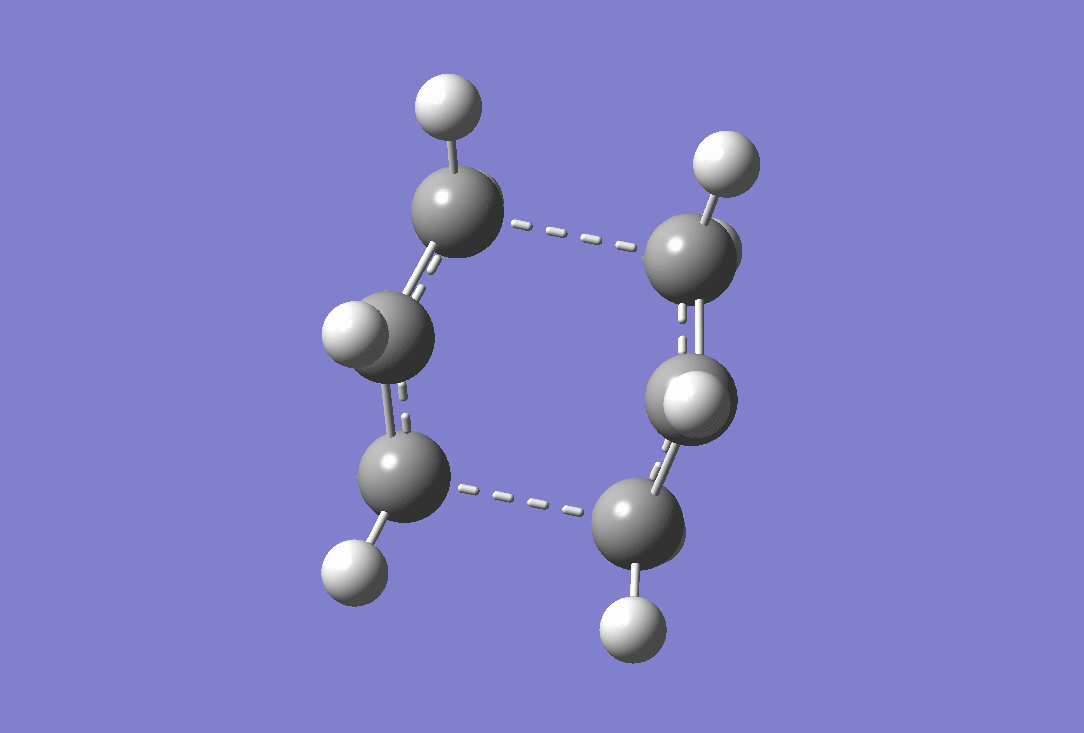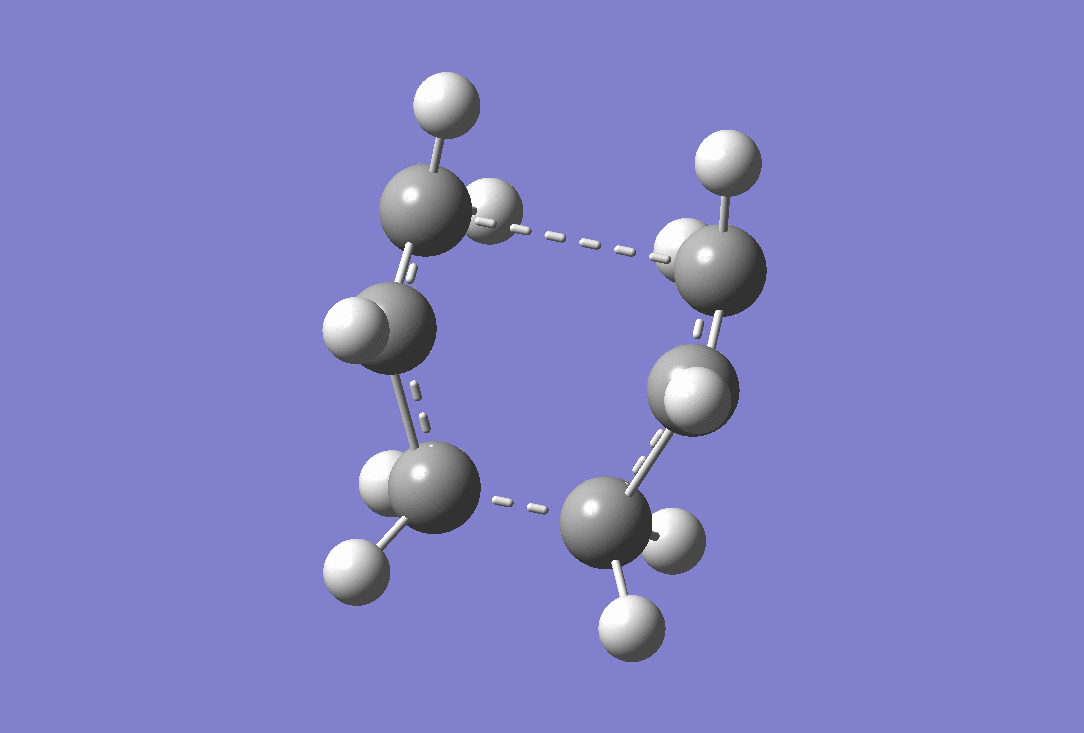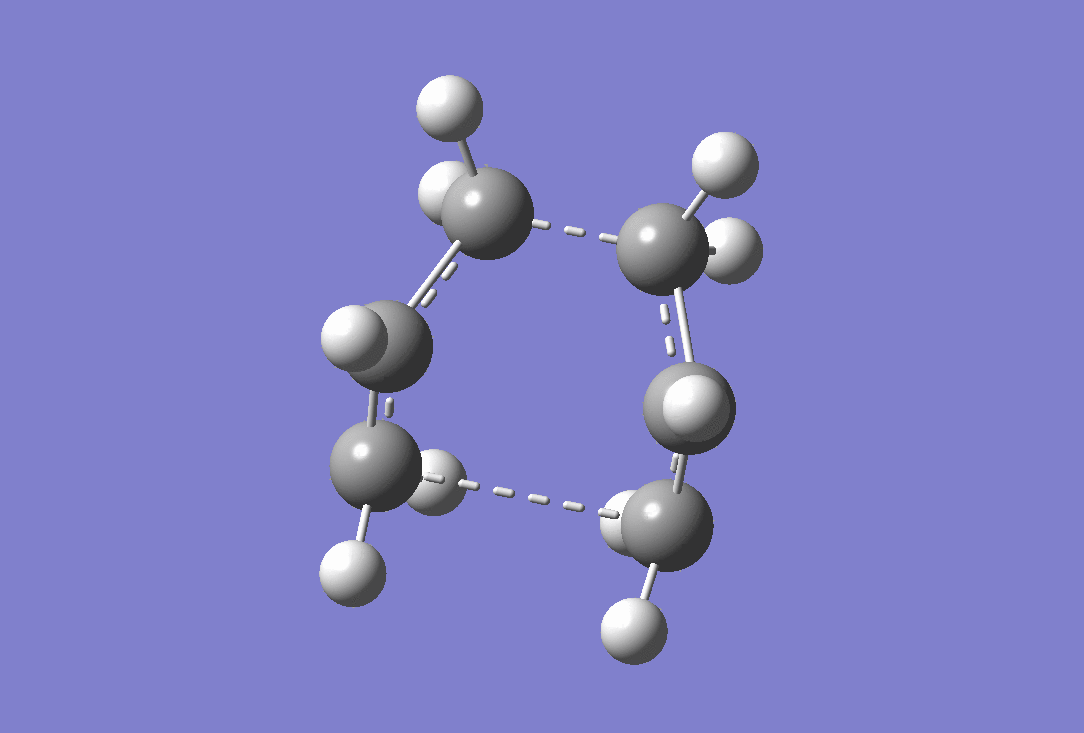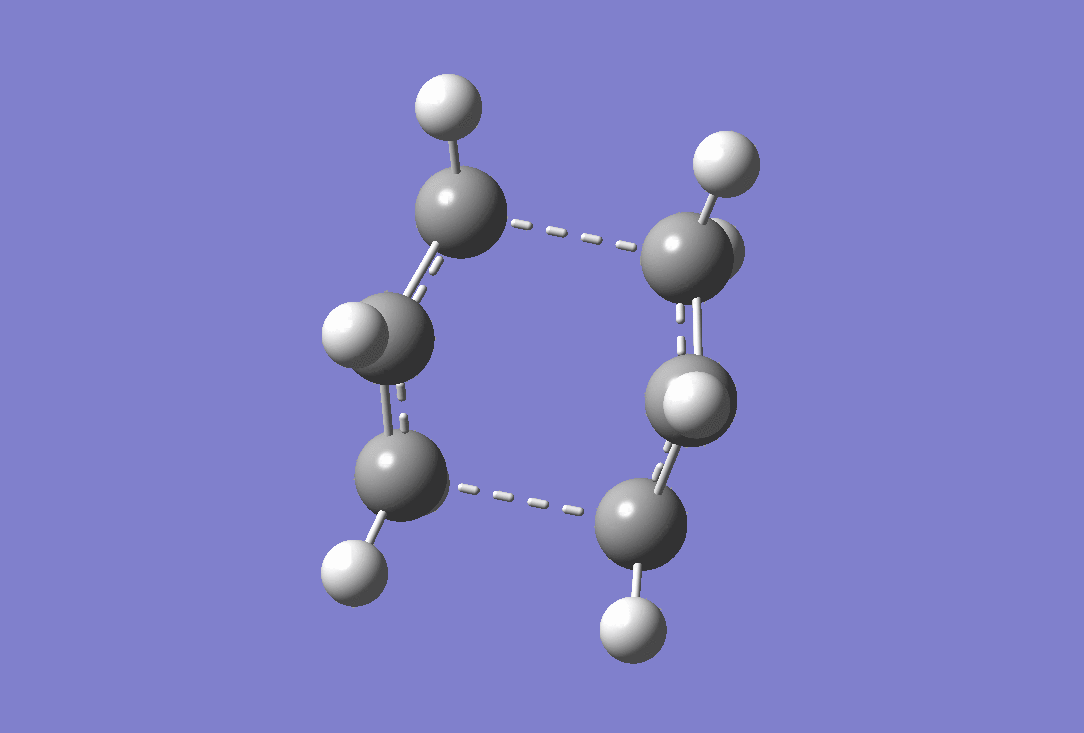

Nf710 (talk) 10:24, 21 April 2016 (BST) Correct frequencies obtained

Intrinsic Reaction Coordinate

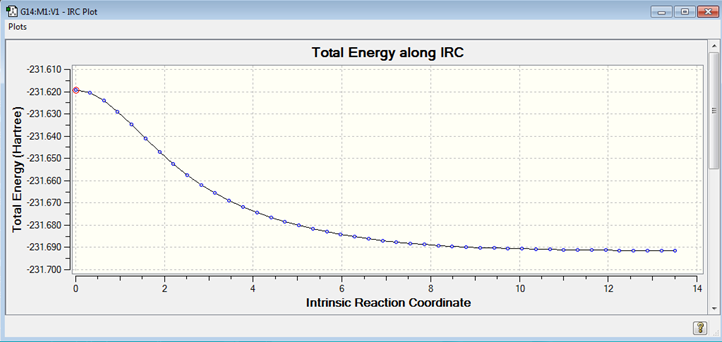
An IRC is used to provide the reaction pathway from the transition structure. This allows you to follow the minimum energy path from a transition structure down to its local minimum on a potential energy surface. It creates a series of points by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest. An IRC can be run in both the forwards and backwards directions as when you are at a transition state, you can descend either side. However, for a symmetrical reaction co-ordinate it is only necessary to run it in one direction. The chair TS IRC ran for 44 steps before reaching completion.

Activation Energies

	HF/3-21G			B3LYP/6-31G*
	Electronic Energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic Energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619322	-231.466697	-231.461338	-234.557020	-234.414921	-234.408999
Boat TS	-231.602802	-231.450932	-231.445299	-234.542989	-234.402346	-234.396020
Reactant (Anti2)	-231.692535	-231.539602	-231.523576	-234.511709	-234.469200	-234.461866

1 hartree = 627.509 kcal/mol

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.75	39.05	34.06	33.17	33.5 ± 0.5
ΔE (Boat)	55.64	49.12	41.95	41.32	44.7 ± 2.0

All energies in the table above provide the activation energies in kcal/mol. It can be seen from the table that the higher level optimization is closer to the experimental value. The tables also show that the chair transition structure have a lower electronic energy and so the reaction will occur through the chair transition structure. While the lower level of theory is good for approximating geometries, they are not able to handle energies as effectively.

Nf710 (talk) 10:33, 21 April 2016 (BST) Fairly good report. Yo have done the majority of what you have been asked but you could have gone into alot more detail in the theorey.

The Diels-Alder Cycloaddition

Like the Cope rearrangment, the Diels-Alder cycloaddition is also a concerted pericyclic reaction. π orbitals are used to form new sigma bonds generating a ring structure. 2 pi-bonds are broken and 2 new sigma bonds are formed in the cycloaddition. This reaction requires 2 reactants for an intermolecular reaction, a diene and a dieneophile. There are also intramolecular cycloaddition reaction which require a single reactant with a conjugated pi-system. The cycloaddition is specifically a [4+2] cycloaddition. The diene must be electron rich and the dieneophile must be electron poor to ensure good orbital overlap between the low-lying LUMO and the high energy HOMO. The smaller the energy gap between these orbitals, the greater the interaction energy. Symmetry properties are also key for this reaction as the reaction may be thermally forbidden in which case photochemistry will be required. To determine whether the reaction is thermally allowed, Woodward-Hoffmann analysis is required.^[7]

(Could you give an example/reference to an intramolecular DA reaction? Tam10 (talk) 17:24, 7 April 2016 (BST))

The reaction taking place now is a DA addition between cis butadiene and ethene along with, cyclohexadiene and maleic anhydride. The electronegative oxygen atoms in maleic anhydride make this an electron poor dieneophile and the electron donating alkyl groups on the diene make it electron rich so the reaction will occur under "Normal electron Demand".^[8]

The "Semi-emperical AM1" method was used to optimize the reactants and products in this case due to its ability to use numerous approximations, speeding up the process. This is particularly useful in this case as more complex molecules are being used. This method is very useful for quickly generating "guess" structures before applying a computationally more expensive method such as B3LYP.

Optimizing cis butadiene

Structure	Results Summary	Point Group	Energy
		C_2v	0.04879719

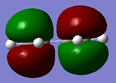
From this optimization, HOMO and LUMO orbitals could be analysed.

cis butadiene HOMO	cis butadiene LUMO

It can be seen that the HOMO is antisymmetric with respect to the plane while the LUMO is symmetric.

Optimizing ethene

Structure	Results Summary	Point Group	Energy
		D_2h	0.02619028

Ethene HOMO	Ethene LUMO

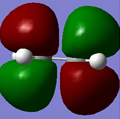
The HOMO is symmetric with respect to the plane, where as the LUMO is antisymmetric.

Optimizing to a Transition Structure

Using the previously optimized cis butadiene and ethene, a transition structure will be generated. The inter-fragment distances input were 2.2 Å and 2.0 Å. Once optimized, the geometry changed, resulting in inter-fragment distances of 2.11930 Å and 2.11916 Å respectively. An imagnary frequency was present at 956.19 cm^-1, proving a transition state has been reached, the animation of which is shown below. The animation shows that the reaction is concerted as the fragments move towards each other in a synchronous fashion.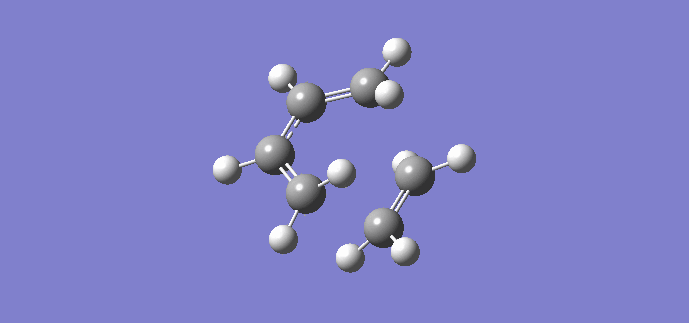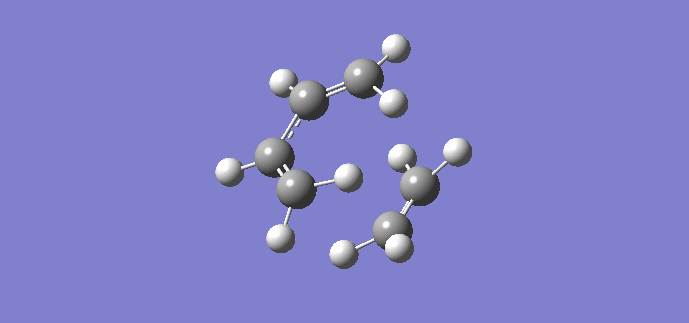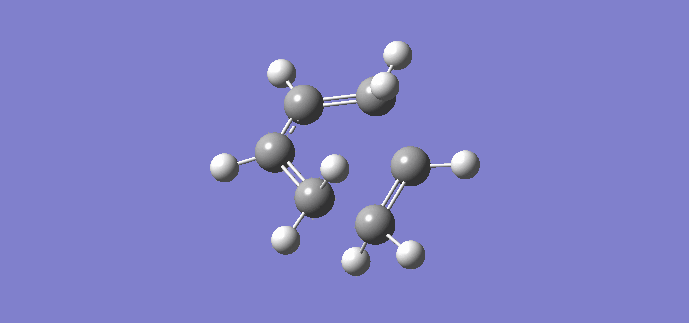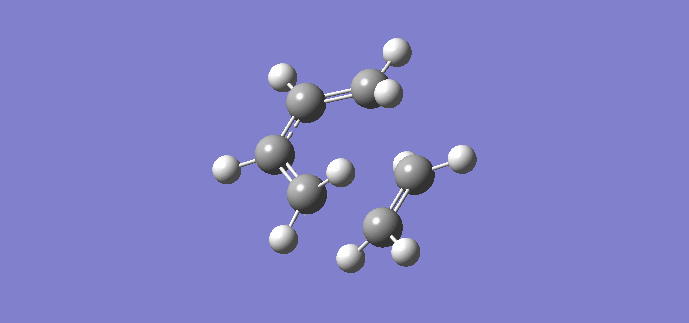

(Avoid putting images in the same line as a paragraph - leads to some strange effects on visualisation Tam10 (talk) 17:24, 7 April 2016 (BST))

The lowest positive frequency is at 147.12 cm^-1. The animation for this (which is below) shows that it does not assist in the formation of the transition state. As the animation shows that at this frequency, the ethene molecule is simply rotating not forming any bonds.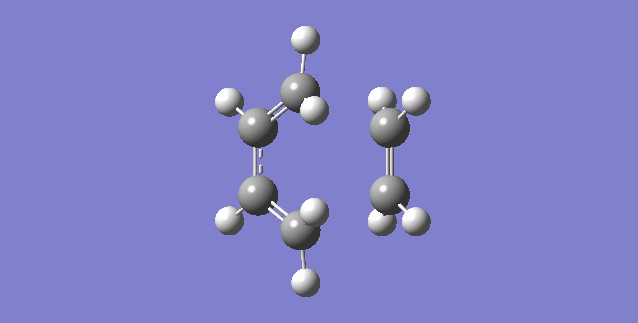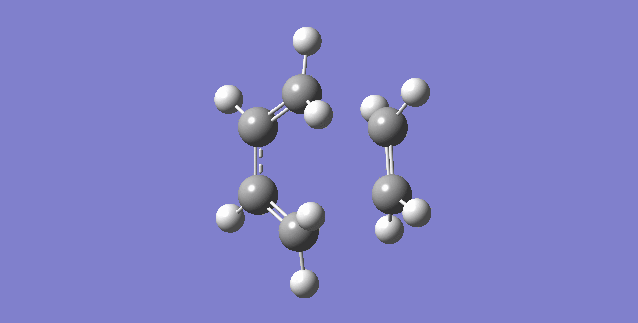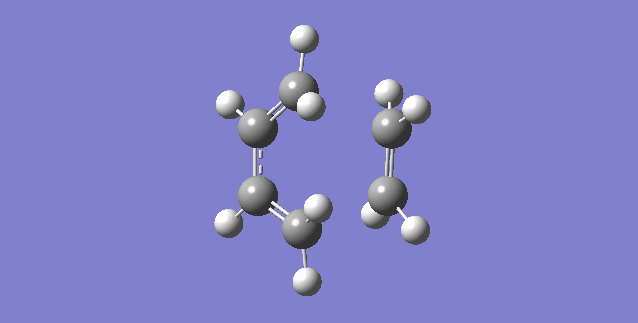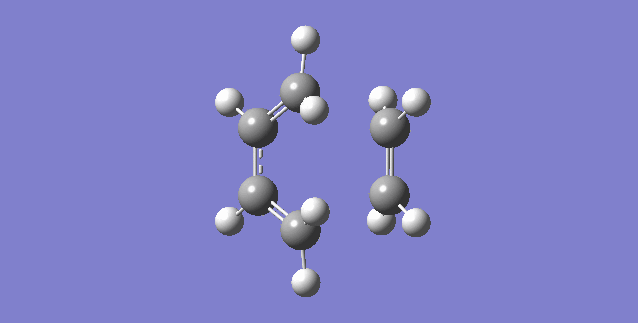

TS HOMO	TS LUMO

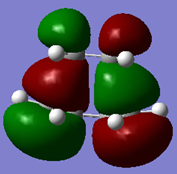
The MOs above show that the HOMO is antisymmetric with respect to the plane and the LUMO is symmetric with respect to the plane. Relative to the reactants, it can be seen that the antisymmetric HOMO of cis butadiene combines with the antisymmetric LUMO of the ethene to form the transition structure HOMO. The symmetric LUMO of the cis butadiene and the symmetric HOMO of the ethene combine to form the symmetric transition structure LUMO. The matching symmetry of these orbitals allows the combination.

Atom	Bond Length (Å)
C1-C10	2.11916
C10-C13	1.38183
C13-C15	1.39748
C15-C7	1.38146
C7-C4	2.11930

As shown in the table, the lengths between C1-C10 and C7-C4 are below 2 x Van der Waals radii, indicating bond formation. With regard to the remaining bonds, the bond length is higher than that seen in C=C double bonds but lower than that observed in C-C single bonds. This indicates that these bonds are between single and double bonds undergoing transitions to their respective product bond. Typical sp³ C-C bond length is 1.54 Å and typical sp² C=C bond length is approximately 1.36 Å. ^[5]The Van der Waals radius of carbon is 1.7 Å.^[6]

Regioselectivity of Diels-Alder Reaction

This reaction can form 2 products, endo and exo. The purpose of this section si to determine which is energetically favourable and the preferred transition structure.

Optimization of cyclohexa-1,3-diene

Structure	Results Summary	Point Group	Energy
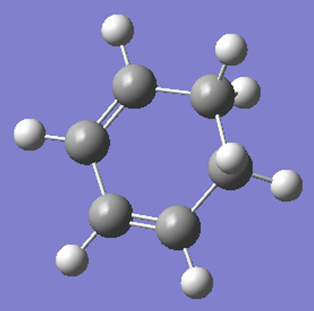
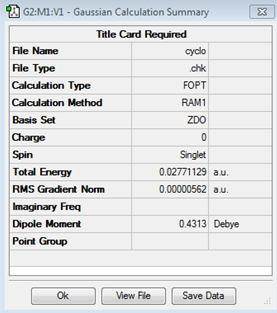
		C₂	0.02771129

HOMO	LUMO

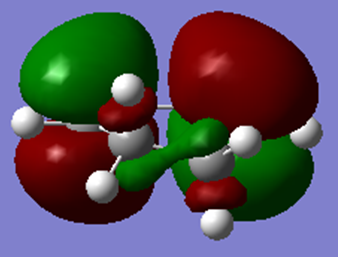
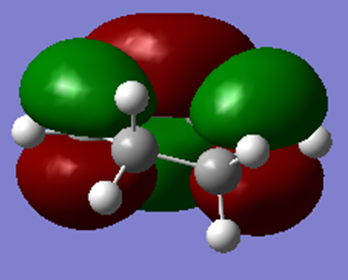
Looking at the MOs above, it can be seen that the HOMO is antisymmetric and the LUMO is symmetric with respect to the plane.

Optimization of maleic anhydride

Structure	Results Summary	Point Group	energy
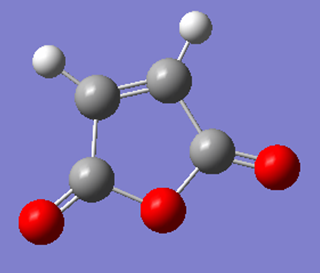
		C_s	-0.12182418

HOMO	LUMO

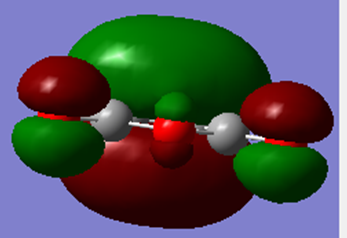
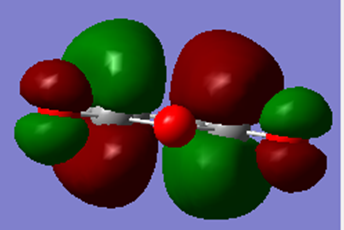
From the MOs above, it can be seen that the HOMO for maleic anhydride is symmetric and the LUMO is antisymmetric with respect to the plane.

Optimization of the Exo Product

Structure	Results Summary	Point Group	Energy
		C₁	-0.15990928

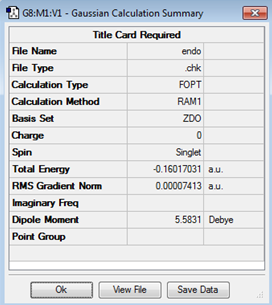
Optimization of Endo Product

Structure	Results Summary	Point Group	Energy
		C₁	-0.16017031

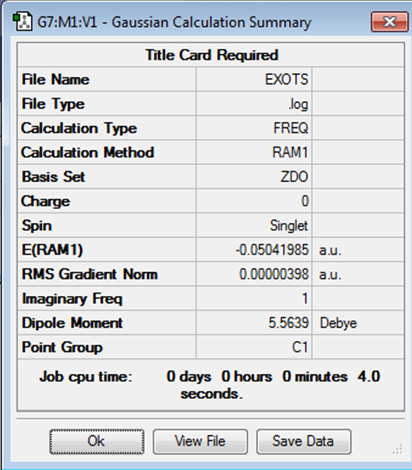
Optimizing to exo transition structure

For this method, I worked backwards from the product molecule, increasing distance between reactant atoms to 2.0 Å. The method used was semi-emperical AM1 as seen earlier.

Structure	Results Summary	Point Group	Energy
		C₁	-0.05041985

A negative frequency was observed at -812.23 cm^-1. The vibration for this is shown below.

HOMO	LUMO

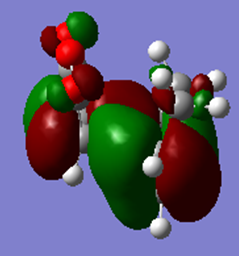
It can be seen from this table that the HOMO is antisymmetric and the LUMO is symmetric.

Structure	Atoms	Bond Length (Å)
	C9-C2	2.17040
	C11-C3	2.17037
	C3-C15	1.38944
	C15-C17	1.39677
	C17-C2	1.39438
	C2-C1	1.48976
	C1-C4	1.52208
	C4-C3	1.48977
	C9-C11	1.41011
	C11-C20	1.48820
	C20-O21	1.40963
	O21-C19	1.40963
	C19-C9	1.48821
	C19-O22	1.22053

The through space distance between C19-H5, of around 2.41624 Å, provides the greatest steric interaction. (Yes, this is a large contribution to the higher exo TS. Watch out that you're quoting lengths to a very high precision - two or three decimals is more appropriate Tam10 (talk) 17:24, 7 April 2016 (BST))

Optimizing to endo transition structure

A similar approach was taken for this as the exo structure above.

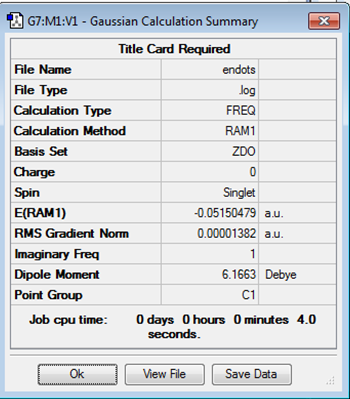
Structure	Results Summary	Point Group	Energy
		C₁	-0.05150479

A negative vibrational frequency was observed at -806.57 cm^-1. The animation of this vibration is shown below.

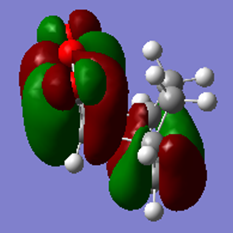
HOMO	LUMO

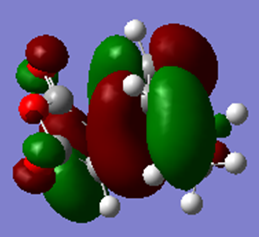
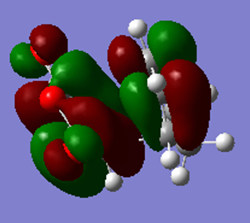
The table shows that both the HOMO and the LUMO are antisymmetric with respect to the plane.

Structure	Atoms	Bond Length (Å)
	C11-C3	2.16248
	C9-C2	2.16218
	C2-C1	1.49055
	C1-C4	1.52296
	C4-C3	1.49052
	C3-C15	1.39306
	C15-C17	1.39728
	C17-C2	1.39306
	C9-C11	1.40848
	C11-C19	1.48924
	C19-O21	1.40896
	O21-C20	1.40894

Relative to the exo transition structure, the C19-H16 through space distance is 3.08346 Å so not sterically hindered. However, H12-H7 provides strong steric repulsion with a through space distance of 2.23190 Å.

Exo vs Endo

From the energies above, it can be seen that the endo transition structure has the lower energy. The bond length analysis in the sections above show that for C-C single bonds, the endo transition structure has shorter bonds. This is due to the greater orbital overlap in the endo TS relative to the exo TS. The bond length between the maleic acid and cyclohexa-1,3-diene in both the exo and endo transition structure is below the Van der Waals radius of 2 carbon atoms of 3.4 Å. The shorter bonds on the endo transition structure indicate a less strained structure at the reacting centre. The maleic acid is able to get closer to the reacting centre in the endo transition structure for this reason. Due to the exo TS having longer bonds, the strain is increased relative to the endo TS. This causes the stabilizing effect of secondary orbital interactions to allow the endo TS to dominate.

(You need to compared your energies numerically. Converting the difference into a unit such as kJ/mol or kcal/mol would make it easy to see what the difference between them is Tam10 (talk) 17:24, 7 April 2016 (BST)) (Secondary orbital interactions are caused by the favourable alignment of orbitals that are not directly involved in the reaction. Endo has them as the pi system of C15 and C17 is close enough to C19(=O23)-O21-C20(=O22) Tam10 (talk) 17:24, 7 April 2016 (BST))

Secondary Orbital Overlap Effect

Due to additional orbital interactions, the endo product is preferred relative to the exo product which doesn't have these interactions. In both cases, primary orbital overlap is present. These additional interactions which do not contribute to bonding (non-bonding) lower the activation energy providing a faster pathway for the reaction to proceed. ^[9] For this reason, the endo is the kinetic product. Under thermodynamic conditions, the exo product will be favoured. The orientation of the approach determines whether there will be stabilization from secondary orbital interactions.

Conclusion

In the first part of the experiment, anti3, gauche, gauche3 and anti 2 were created and optimized under the HF/3-21G level. For the simple molecules being optimized, this method provided a high degree of accuracy in terms of geometry and energy. Optimization to a transition state confirmed the reaction proceeds in a synchronous fashion. The chair and boat structures produced under QST2 required a reasonable guess of the transition state which can prove to be a limitation in more complex molecules. Initially the boat TS failed due to the inability of QST2 to consider bond rotations. QST3 improves the reliability as it allows an input of geometry.

For the Diels Alder cycloaddition, the AM1 proved to be useful as it is fast and reasonably accurate. PM6 can be applied to a greater set of systems as it is more parameterized. This allows for the generation of guess structures. It would be beneficial to implement more complex molecules to determine the variation between theory and observed energies and geometries.

References

[1] Grimes R. W., Catlow C.R.A.. Quantum Mechanical Cluster Calculations in Solid State Studies. Singapore: World Scientific Publishing Co. Pte. Ltd; 1992.

[2] Hasanein A.A., Evans M.W. Computational Methods in Quantum Chemistry, Volume 2: Quantum Chemistry. Singapore: World Scientific Publishing Co. Pte. Ltd; 1996.

[3] Computational Methods for Large Systems: Electronic Structure Approaches for Biotechnology and Nanotechnology - By Jeffrey R. Reimers

[4] Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics By Errol G. Lewars

[5] Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. Springer.

[6] Bondi, A. (1964). "Van der Waals Volumes and Radii". J. Phys. Chem. 68 (3): 441–51. doi:10.1021/j100785a001.

[7] Dewar, M. J.; Olivella, S.; Stewart, J. J. (1986). "Mechanism of the Diels-Alder reaction: Reactions of butadiene with ethylene and cyanoethylenes". Journal of the American Chemical Society 108 (19): 5771–5779. doi:10.1021/ja00279a018.

[8] Kloetzel, M. C. (1948). "The Diels-Alder Reaction with Maleic Anhydride". Organic Reactions 4: 1–59. doi:10.1002/0471264180.or004.01.

[9] Fleming, Ian (1978). Frontier Orbitals and Organic Chemical Reactions. London: Wiley. pp. 29–109.