Dat's Wiki Page

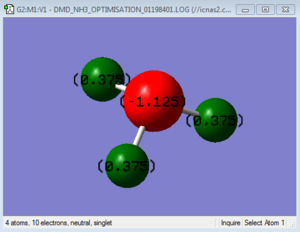
NH3 molecule

Summary information

N-H bond distance	1.01798
H-N-H bond angle	105.741
Calculation method	B3LYP
Basis set	6-31G(d,p)
Final energy E(RB3LYP) in au	-56.55776873
RMS gradient	0.00000485
Point Group	C3V

Optimisation


         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
 Predicted change in Energy=-5.986269D-10
 Optimization completed.
    -- Stationary point found.

NH3

The optimisation file is linked to here

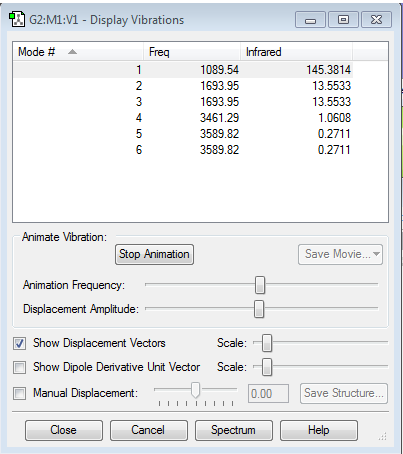
Vibrations and charges of NH₃

How many modes do you expect from the 3N-6 rule?

6

Which modes are degenerate (ie have the same energy)?

2 and 3, 5 and 6

Which modes are "bending" vibrations and which are "bond stretch" vibrations?

1,2 and 3 are bending vibrations, 4,5 and 6 are bond stretch vibrations

Which mode is highly symmetric?

4

One mode is known as the "umbrella" mode, which one is this?

1

How many bands would you expect to see in an experimental spectrum of gaseous ammonia?

2 bands because there are two large peaks, but the other peaks are too small relative to the larger peaks so are not counted.

Charge Distribution

H2 Molecule

Summary information

H-H bond distance	0.74279
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy E(RB3LYP) in au	-1.17853936
RMS gradient	0.00000017
Point Group	D_∞h

Optimisation


         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
 Predicted change in Energy=-1.164080D-13
 Optimization completed.
    -- Stationary point found.

H2

The optimisation file is linked to here

N2 Molecule

Summary information

N-N bond distance	1.10550
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy E(RB3LYP) in au	-109.52412868
RMS gradient	0.00000365
Point Group	D_∞h

Optimisation

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES
 Predicted change in Energy=-3.401029D-13
 Optimization completed.
    -- Stationary point found.

N2

The optimisation file is linked to here

Haber-Bosch process

N₂ + 3H₂ --> 2NH₃


E(NH3)= -56.55776873
2*E(NH3)= -113.1155375
E(N2)= -109.52412868
E(H2)= -1.17853936
3*E(H2)= -3.53561808
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 au
ΔE= -146.478599028 kJ/mol
ΔE= -146.48 kJ/mol (2dp)

The ammonia product is the most stable as the formation of ammonia is a exothermic reaction so energy is released to form a more stable product.

The literature value for the formation of ammonia in the Haber Bosch process is -91.2kJ/mol.^[1] This literature value is very different from the calculated value because the literature value is experimentally calculated under standard conditions such as 298K. The computer calculated energies are calculated under conditions assumed to be for example 0K. Therefore the energy values from the computer are very different from the experimentally calculated enthalpies.

F2 molecule

Summary information

F-F bond distance	1.40298
Calculation method	RB3LYP
Basis set	6-31G(d,p)
Final energy E(RB3LYP) in au	-199.49825220
RMS gradient	0.00000069
Point Group	D_∞h

The literature value of the F-F bond length is 1.41 angstroms .^[2] This literature value is very close to the calculated F-F bond length because the computer can calculate the first derivative of the potential energy surface which provides us of the structure we want.

Optimisation

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000001     0.001800     YES
 RMS     Displacement     0.000002     0.001200     YES
 Predicted change in Energy=-1.747692D-12
 Optimization completed.
    -- Stationary point found.

F2

The optimisation file is linked to here

F₂ is a fully symmetrical molecule and is linear and so has an equal charge distribution.

Molecular Orbitals of F₂

Molecular Orbitals of F₂
Image	Description
	The highlighted orbitals show the energies of the molecular orbitals (MOs) I have chosen.
	These are the axes I will use to describe my molecular orbitals.
	1 - The core 1s orbitals of fluorine are very deep in energy and very penetrating. They are so contracted and so won't overlap as shown in the MO diagram.
	3 - This is a σ_g MO formed by the overlap of two 2s AOs in the same phase. It is quite low in energy as it is lower than all MOs formed from the overlap of 2p orbitals. It is also occupied but doesn't contribute to the F-F bond as the σ_u* antibonding MO for two 2s AOs is filled.
	4 - This is the σ_u* antibonding MO formed by the overlap of two 2s AOs of opposite phase. It is higher in energy than MO 3 but is lower in energy than all MOs formed from the overlap of 2p orbitals. This antibonding MO is occupied.
	8 - This is the π_g* antibonding MO formed by the overlap of two 2px AOs of opposite phase. It is quite high in energy as it is an antibonding MO formed from 2p orbitals which are higher in energy than 2s orbitals. It is also the HOMO.
	10 - This is the σ_u* antibonding MO formed by the overlap of two 2pz AOs of opposite phase. It is the highest energy MO and is also the LUMO as it is the only unoccupied MO formed. Because it is unoccupied, this gives a bond order of 1 (8-6/2) and so a single F-F molecule describes the F2 molecule.