Rep:Mod:DJW404

Conformational Analysis Using Molecular Mechanics

The Hydrogenation of Cyclopentadiene Dimer

Structures of the cyclopentadiene dimer (1,2) and the two hydrogenated products of 2 (3,4)

Diagram showing the difference between the thermodynamic product and the kinetic product

Table 1 - Click molecule names to view structures

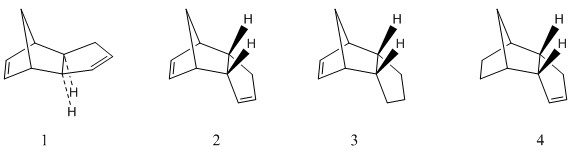
Molecule	Total energy (kCal/mol)	Total bond stretching energy (kCal/mol)	Total angle bending energy (kCal/mol)	Total torsional energy (kCal/mol)	Total van der Waals energy (kCal/mol)	Total electrostatic energy (kCal/mol)
Exo dimer (1)	55.37344	3.54298	30.77289	-2.73086	12.80126	13.01371
Endo dimer (2)	58.19070	3.46739	33.19139	-2.94948	12.35721	14.18433
Hydrogenation product (3)	50.44567	3.31130	31.93653	-1.47006	13.63738	5.11951
Hydrogenation product (4)	41.25749	2.82296	24.68574	-0.37807	10.63670	5.14702

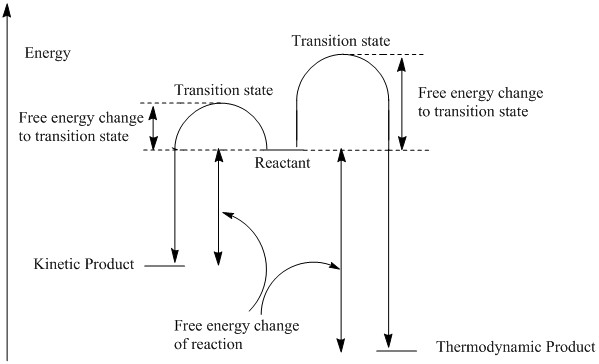
The geometries of the two dimers of cyclopentadiene were optimised using the MMFF94s forcefield. The results of the optimisations are summarised in table 1. The results show that the thermodynamically favoured minimum energy conformation of the dimer is the exo dimer, not the endo dimer which is experimentally observed. This suggests that the dimerisation selectivity is not governed by the thermodynamic stability (as this would lead to the exo product). The transition state for the dimerisation leading to the endo product is therefore probably lower in energy and the reaction selectivity controlled by kinetic factors. The difference between the thermodynammic reaction path and the kinetic reaction path is illustrated in the diagram.

The two dihydro derivatives of the endo conformer were again optimised using the same MMFF94s forcefield. The results are also summarised in table 1. the results show that hydrogenation product (3) is lower in energy and therefore more stable than hydrogenation product (4). Looking at the relative contributions from each factor, while the electrostatic contribution and the torsional energy are lower for product (4), the other factors all favour product (3).

Atropisomerism in an Intermediate related to the Synthesis of Taxol

Intermediates in the synthesis of taxol

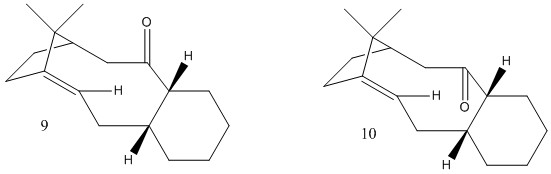
The structures of two atropisomers of the intermediate in the synthesis of Taxol were optimised using the MMFF94s force-field. The results are summarised in table 2. Atropisomers are isomers that are conformationally separated by the rotation of a single bond.

Relationship between different Taxol intermediate structures

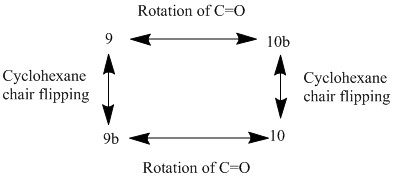
The completely minimised structures for the Taxol intermediates were hard to obtain because of the large degree of conformational freedom within the molecule. This meant that finding the correct structure required some manual manipulation to get all bonds into the correct orientations. The first two structures are the lowest energy structures, with the cyclohexane group in the chair conformation. The second two structures in table 2 (9b and 10b) differ from structures 9 and 10 in the configuration of the cyclohexane group (different chair conformation) and both give higher energies. If these two configurations were found and assumed to be the minimum energy conformations then the ordering of the conformers with respect to the energies would be wrong. The relationships between the four structures in the table are shown in the diagram. This means that the energy barrier between 9 and 10 is not just due to the energy associated with the rotation of the carbonyl group but also the energy associated with ring flipping of the cyclohexane group. Structures 9c and 10c both have twist boat conformations and are both higher in energy than the minimum energy chair conformations. It is interesting to note that the boat conformations are lower in energy and thus more stable than the higher energy chair conformations.

Bond angles of the alkene in the lowest energy conformations of the two taxol intermediates (all angles are in degrees)

Table 2 - Click molecule names to view structures

Molecule	Total energy (kCal/mol)	Total bond stretching energy (kCal/mol)	Total angle bending energy (kCal/mol)	Total torsional energy (kCal/mol)	Total van der Waals energy (kCal/mol)	Total electrostatic energy (kCal/mol)
Taxol intermediate (9) Chair	70.54367	7.70627	28.31850	0.10230	33.21079	0.30024
Taxol intermediate (10) Chair	60.55377	7.61780	18.82559	0.19603	33.26480	-0.05548
Taxol intermediate (9b) Chair	83.71668	8.07632	35.73324	3.65187	34.35841	0.17321
Taxol intermediate (10b) Chair	74.89893	8.54150	21.49387	7.25142	35.79315	0.43814
Taxol intermediate (9c) Boat	76.28936	7.94940	29.48607	2.77935	34.72395	0.31644
Taxol intermediate (10c) Boat	66.31628	7.76294	19.01892	3.79057	34.98250	-0.06037
Hydrogenated Taxol intermediate (9) Chair	81.75224	6.94339	32.04095	9.50639	32.70568	0.00000
Hydrogenated Taxol intermediate (10) Chair	71.43756	6.58715	24.76522	8.40255	31.18402	0.00000

Table 3 - Click molecule names to view structures

Molecule	Total energy (kCal/mol)	Total angle bending energy (kCal/mol)	Total torsional energy (kCal/mol)
Alkene	53.94489	16.76091	10.25654
Hydrogenated Alkene	15.37117	6.28104	-3.55842

The most stable isomer found is (10). As can be seen from the table, the difference is almost entirely accounted for by the difference in the contributions from the angle bending energy. The bond angles around the alkene in both structures are shown in diagram 3. The deviations of the angles for structure 10 from the ideal values of 120° for a planar sp² are all either equal or smaller to the deviations from 120° in structure 9. The carbonyl CCC bond angles are also significantly different in the two structures, with the angle for structure 10 (118.3°) being much closer to the ideal value of 120° than for structure 9 (123.4°). The increased bending of the bond angles in structure 9 add together to raise the energy of the overall structure, making it less stable than structure 10.

The structure of 9 causes it to adopt a more strained structure with unfavourable bond angles. This makes the structure less stable than structure 10. This is referred to as olefin strain. The olefin strain (OS) energy is denfined as the difference in strain energy between an olefin and it's hydrogenated counterpart. The two major contributions to this are the torsional strain energy and the angle bending strain energy. An OS of 24.4 for another constrained alkene, results summarised in table 3 for an unstable alkene compares with a negative olefin strain for the molecules under study. This stability of the olefin in the Taxol intermediate (the total energy increases upon hydrogentation) accounts for why it is observed to be unreactive.

Spectrocopic Simulation using Quantum Mechanics

Optimisation of Taxol intermediates 17 and 18

Table 4 - Click molecule names to view structures

Molecule	Total energy (kCal/mol)	Total bond stretching energy (kCal/mol)	Total angle bending energy (kCal/mol)	Total torsional energy (kCal/mol)	Total van der Waals energy (kCal/mol)	Total electrostatic energy (kCal/mol)
Taxol intermediate (18) Chair	100.46535	15.00553	30.91071	9.71977	49.32278	-6.01077
Taxol intermediate (18) Twist-Boat	102.20994	15.46615	28.98120	12.85489	52.61916	-9.00992

The intermediates 17 and 18 were optimised, again using the MMFF94s force field, and found to have a different lowest energy conformation than intermediates 9 and 10. The results are summarised in table 4. Although the lowest energy conformation had a chair cyclohexane group, the lowest boat conformation was also very close in energy. These geometries were then submitted to GAUSSIAN software for a finer optimisation and calculation of an NMR spectrum. The GAUSSIAN calculations were done with B3LYP theory level using the 6-31G(d,p) basis set with the SCRF solvent system (benzene chosen as the solvent for comparison with literature values). The energy was also corrected for dispersion interactions using the "EmpiricalDispersion=GD3" keyword.

Deviations of the ¹³C NMR calculated shifts from the actual shifts

Chair ¹³C NMR spectrum

Chair ¹H NMR spectrum (Degeneracies included to improve readability)

Boat ¹³C NMR spectrum

Boat ¹H NMR spectrum (Degeneracies included to improve readability)

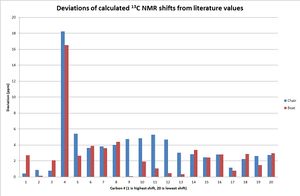
The sum of the electronic and thermal free energies can be used to compare the relative energies of two isomers of the molecule. Although the chair form is calculated to be lower in energy than the boat form, both values are close and so both forms were used to calculate the NMR spectrum of the molecule. The deivations of the two ¹³C NMR spectra from the literature values are shown in the chart. Since it is hard to individually assign all the carbons the deviations were calculated from the literature carbon in the same position if all the carbons were ordered by the chemical shift. The overall result was the same if only the carbons that had the same rank in both the chair and boat calculations were included. The sum of the deviations was lower for the boat configuration (2.8ppm for boat vs 3.8 ppm for the chair), indicating that the boat conformer might actually be the experimentally observed one although they were both reasonably close to the literature.

In both cases the shift for the carbonyl carbon (1 in the chart), the two alkene carbons (3 and 6 in the chart) were all very close to the literature values. On the other hand, the carbon bonded to both S atoms was calculated to be considerably higher in shift than is observed experimentally.

Chair:
 Sum of electronic and zero-point Energies=          -1651.415410
 Sum of electronic and thermal Energies=             -1651.394012
 Sum of electronic and thermal Enthalpies=           -1651.393067
 Sum of electronic and thermal Free Energies=        -1651.462141

Twist-Boat:
 Sum of electronic and zero-point Energies=          -1651.410650
 Sum of electronic and thermal Energies=             -1651.389074
 Sum of electronic and thermal Enthalpies=           -1651.388129
 Sum of electronic and thermal Free Energies=        -1651.457741

Analysis of the properties of the synthesised epoxides

Four epoxides were synthesised in the organic laboratory using the shi and jacobsen catalysts. They were investigated here using computational methods in order to rationalise the selectivity of the catalysts observed experimentally. The structures are shown in the diagram.

Catalyst crystal structure

Catalyst Structures

Shi Catalyst OCO bond distances and angles

Shi catalyst favourable vdW interactions

Favourable H-H contacts in Jacobsen catalyst

Favourable O-H contacts in Jacobsen catalyst

The ConQuest software package was used to search the Cambridge crystal database to find the crystal structures of the two catalysts under study. The two catalysts were the Shi catalyst (21) and the Jacobsen catalyst (24).

Shi Catalyst

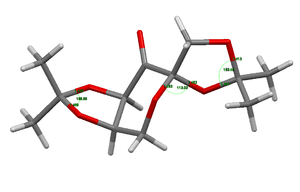
The crystal structure of the Shi catalyst was analysed to investigate its configuration. The carbon atom on the ring that is bound to two oxygen atoms is quite different in configuration to the other two OCO centres. The angle between the two C-O bonds for the 6-membered ring carbon atom is wider and the bond lengths shorter.

Jacobsen Catalyst

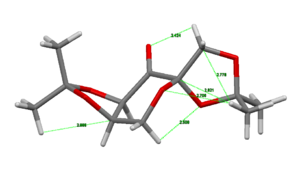
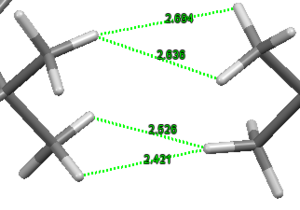
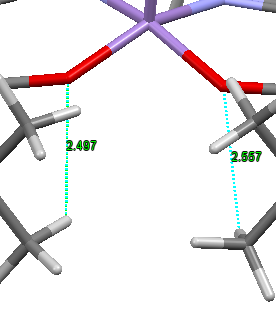
The Jacobsen catalyst was analysed to investigate any favourable intramolecular interactions. The crystal structure was first analysed to find favourable H-H van der Waals contacts (~2.4Å) . This analysis showed only 4 contacts between H atoms separated by more than 5 bonds; which were between the adjacent ^tBu groups. The bond distances are shown in the image. There are many more of these contacts between atoms separated by fewer than 5 bonds but they were not considered to have a strong effect on the structure since as they are so close simply due to being separated by fewer bonds. The structure was also searched for any favourable OH interactions. There were two favourable interactions found, shown in the second image, both close to the optimum O-H distance (2.62Å) between the O atoms bound to the Mn centre and the closest hydrogen atoms on the tBu groups discussed above.

NMR Analysis of epoxidised products

Table 5 - Click molecule names to view structures

Molecule	doi	1H NMR	13C NMR	Literature values
R,S-dihydronapthalene Oxide	DOI:10042/28132			1H NMR (400 MHz, CDCl3) δ 7.39 (d, J = 7.3 Hz, 1H), 7.28 – 7.18 (m, 2H), 7.08 (d, J = 7.3 Hz, 1H), 3.84 (d, J = 4.2 Hz, 1H), 3.73 (s, 1H), 2.89 – 2.71 (m, 1H), 2.54 (dd, J = 15.5, 5.5 Hz, 1H), 2.41 (dd, J = 14.2, 6.4 Hz, 1H), 1.76 (td, J = 13.9, 5.6 Hz, 1H); 13C NMR (100 MHz, CDCl3) δ 137.26 (s), 130.11 (s), 128.99 (d, J = 3.0 Hz), 126.69 (s), 55.68 (s), 53.34 (s), 24.96 (s), 22.39 (s)
R,R-Stilbene Oxide	DOI:10042/28133			1H NMR (400 MHz; CDCl3) δ=3.95 (2H, s), 7.40-7.55 (10H, m); 13C NMR (100 MHz; CDCl3) δ=137.1, 128.5, 128.2, 125.5, 62.7

The NMR for the epoxidised products were calculated using an initial optimisation under the MMFF94s forcefield, followed by an optimisation and frequency analysis using the B3LYP hybrid functional and the 6-31G(d,p) basis set. The structures and NMR spectra can be found in table 5.

The napthalene oxide ¹H NMR has the correct degeneracies and genrally similar chemical shifts with an error of around 0.25ppm.

The ¹³C NMR for the napthalene oxide shows genrally good agreement with literature, especially for the aryl carbon atoms but much poorer agreement with literature for the alkyl carbon atoms.

The ¹H NMR for Stilbene oxide shows good agreement with literature for the aryl protons, with 10 protons between 7.47 ppm and 7.57 ppm compared with the literature value of 7.4-7.55 ppm. The epoxide protons are slightly further from the literature value at 3.53ppm compared with the literature value of 3.95 ppm.

The ¹³C NMR for Stilbene oxide also shows good agreement with literature. The epoxide carbon atoms are slightly different (calculated as 66.4 ppm vs lit. 62.7). The aryl carbon atom calculated shifts are slightly more spread out with 118-134 ppm vs 125-137 ppm for the literature value.

Assigning the absolute configuration of the product epoxides using the calculated chiroptical properties

Table 6 - All Optical rotations reported in chloroform, Click molecule names to view structures

Molecule (doi)	Optical Rotation at 589nm (deg)	Optical Rotation at 365nm (deg)	Literature value at 589nm (deg)
Napthalene Epoxide 1R2S (DOI:10042/28204 )	-35.87	-209.45	-38.8;
Napthalene Epoxide 1S2R (DOI:10042/28168 )	35.86	209.46	inferred to be 38.8
trans-Stilbeneoxide RR (DOI:10042/28170 )	297.78	1252.94	250.8
trans-Stilbeneoxide SS (DOI:10042/28171 )	-297.79	-1252.95	Inferred to be -250.8

The optical rotation of both enantiomers of each epoxide were calculated using the CAM-B3LYP method and the 6-311++g(2df,p) basis set. The CAM-B3LYP was used as it includes a number of corrections to improve the accuracy of the optical rotation calculation.

The optical rotatory power of the trans stilbene, epoxidised using Shi catalyst, is reported to be positive. Therefore the calculation suggests that the enantiomer formed in the Shi epoxidation is indeed RR. The calulated value for the optical rotation is higher than is observed experimentally. This suggests that the basis set used in the calculation may have been too small to full describe the system. It is still reasonably close however so the assignment can be made with confidence. This is supported by the calculated value for the opposite enantiomer being very similar in magnitude and negative.

The optical rotation of the 1,2-dihydronapthalene epoxide formed with Shi Catalyst is reported to be negative, the calculation thus suggests that the epoxide formed is the 1R2S. This is however not in agreement with the literature cited which claims that the epoxide synthesised was the 1S2R enantiomer. The literature is therefore suggested to have made an incorrect assignment.

In contrast to the Shi catalyst derivative, the optical rotation of the 1,2-dihydronapthalene epoxide formed with Jacobsen catalyst is reported to have a positive optical rotation. This is correctly identified as the 1S2R enantiomer in the literature cited. This means that the Shi catalyst and the Jacobsen catalyst have opposite selectivity for this substrate.

Transition States

Table 7 - Click configuration to view transition state structure

Transition State (doi)	Sum of electronic and thermal free energies (Hartees)
Dihydronapthalene Jacobsen Catalyst
Jacobsen - 1R2S1 (DOI:10.6084/m9.figshare.909346 )	-3421.359354
Jacobsen - 1R2S2 (DOI:10.6084/m9.figshare.907332 )	-3421.359499
Jacobsen - 1S2R1 (DOI:10.6084/m9.figshare.903752 )	-3421.369033
Jacobsen - 1S2R2 (DOI:10.6084/m9.figshare.907473 )	-3421.361580
Trans-Stilbene Shi Catlayst
Shi - RR1 (DOI:10.6084/m9.figshare.828552 )	-1534.687808
Shi - RR2 (DOI:10.6084/m9.figshare.829522 )	-1534.700037
Shi - RR3 (DOI:10.6084/m9.figshare.829523 )	-1534.699901
Shi - RR4 (DOI:10.6084/m9.figshare.830388 )	-1534.687252
Shi - SS1 (DOI:10.6084/m9.figshare.829524 )	-1534.683440
Shi - SS2 (DOI:10.6084/m9.figshare.829525 )	-1534.685089
Shi - SS3 (DOI:10.6084/m9.figshare.830389 )	-1534.693818
Shi - SS4 (DOI:10.6084/m9.figshare.830390 )	-1534.691858

The S,S and the R,R transition states for the Shi epoxidation of Stilbene and the 1S2R and 1R2S transition states of the Jacobsen epoxidation of 1,2-dihydro napthalene were analysed to determine a theoretical value for the enantiomeric excess of the reaction.

The transition states used were calculated by Professor Henry Rzepa of the Imperial College London Chemistry department and kindly provided for analysis. the calculation method used was RwB97XD using the 6-311G(d,p) basis set. The free energies of the transition states are shown in table 7. It should be noted that the Shi transition states RR2(DOI:10.6084/m9.figshare.829522 ) and RR3(DOI:10.6084/m9.figshare.829523 )are almost identical in energy and geometry. This leads the author to think that the transition states might actually be the result of two optimisations converging to the same transition state, however, for this lab this similarity was ignored.

Shi transitions states RR1, RR4, SS1 and SS2 had the alkene reacting with the oxirane oxygen atom on the same side as the bridged ring while RR2, RR3, SS3 and SS4 had the alkene reacting with the other oxirane. For the Jacobsen trsnsition states, RS1 and SR1 are in an 'endo' type configuration while RS2 and SR2 are in an 'exo' type configuration.

Since the two products from both the Shi catalyst reaction and the Jacobsen catalyst reaction are enantiomers and thus equal in energy, any selectivity is controlled by the transition state of each reaction and so controlled kinetically rather than thermodynamically. The enantiomeric excess can be estimated from the free energies associated with the transition state. The results suggest that the most stable transition state for the Jacobsen catalyst is the 1S2R1 transition state. The most stable Shi catalyst transition state was found to be RR2, followed by RR3 and SS3. For the trans-stilbene, the two transition states for the Jacobsen catalyst, as well as the three most stable transition states for the Shi catalyst were subjected to a NCI analysis, as detailed in the next section.

To calculate the enantiomeric excess the Boltzman distribution can be used. $\frac{N_{ts1}}{N_{ts2}}=e^{\frac{E_2-E_1}{kT}}.$

Where $\frac{N_{ts1}}{N_{ts2}}$ is the ratio of the molecules in each of transition states 1 and 2 with energies $E_1$ and $E_2$ respectively. Since any of the transition states could theoretically lead to reaction, in order to get the correct K value for the equilibrium constant for the Shi catalyst including all 8 possible transition states the relative populations of each state were calculated relative to the highest energy (least populated) energy state (SS1). The equilibrium constant was then calculated as $k_{RR/SS}=\frac{N_{RR1}+N_{RR2}+N_{RR3}+N_{RR4}}{N_{SS1}+N_{SS2}+N_{SS3}+N_{SS4}}$

The enantiomeric excess (ee) is calculated from the equilibrium constant by $ee=\frac{k_{RR/SS}}{k_{RR/SS}+1}$ The calculations give values for K of 1.31×10³ for the Jacobsen and 1.20×10³ for the Shi catalyst, with the 1S2R enatiomer favoured by the Jacobsen catalyst and the RR enantiomer favoured by the Shi Catalyst. These values correspond to an enantiomeric excess of 99.98% for Jacobsen and 99.83% for the Shi catalyst.

While a 99.98% ee sounds unachievable, the Jacobsen reaction with Dihydronapthalene is reported to give an ee varying from 98% at low yields (~60%) to 85-91% at higher yields (~70%). This suggests that the theoretically calculated ee could be obtained under strictly controlled reaction conditions.

The ee for Stilbene with Shi catalyst is also in good agreement with literature; with >95% yields reported. It is interesting to note that the ee has been observed to decrease with increasing reaction time. This also supports the calculated value as it has been assumed that the reaction is kinetically controlled for the above calculation to be valid. Therefore it would be expected that if the system was given longer to equilibrate, a more even distribution between the two enantiomers would be observed (since they are enantiomers, the products of the reaction are equal in energy so under completely thermodynamic conditions a 50:50 racemic mixture would be obtained). It should also be noted however that this increase in the ee again comes at the cost of much lower yield.

Investigating the non-covalent interactions in the active-site of the reaction transition state

The transition states were subjected to a non-covalent interactions (NCI) analysis to qualitatively assess the extent of Van der Waals interactions around the active site of the reaction. It can be seen immediately by comparing the Shi RR transition states and the SS transition state that the RR transition state has significantly more NCIs present (shown as green blobs in the model). These NCIs have the effect of stabilising the transition state and making it lower in energy. This stabilisation means that the kinetic product of the reaction is the RR enantiomer as opposed to the SS enantiomer, even though the products are identical in energy. In all three transition states the new covalent bond forming can be seen as the blue ring between the alkene and the oxygen atom on the catalyst.

For the Jacobsen catalyst transition states, there are significant NCIs between the aryl groups on the stilbene and on the catalyst. The SS transition state seems to have slightly more interactions between the opposing aryl groups of the two molecules but are hard to differentiate by this. This reaction hasn't been reported in literature but the most stable transition state energies are -3574.921174 hartrees for RR and -3574.923087 hartrees for SS. This suggests that the most stable transition state is therefore the SS one. This would be an interesting reaction to investigate since it has never been reported in literature. This absence from literature may be due to the it not being a very reactive transition state. The NCI analysis doesn't show the same blue ring indicating the formation of the new bond as is seen in the Shi catalyst transition states.

Table 8 - NCI analysis of selected stilbene transition states

Jacobsen	Shi RR	Shi SS
Stilbene Jacobsen SS Orbital	Stilbene Shi RR2 Orbital	Stilbene Shi SS3 Orbital
Stilbene Jacobsen RR Orbital	Stilbene Shi RR3 Orbital

Quantum Theory of Atoms in Molecules Analysis

SS3

RR2

RR2

A quantum theory of atoms in molecules (QTAIM) analysis gives information of the bond critical points (BCPs), which are the points with a zero derivative in every direction with respect to the electron density. this means that they are generally the point at which the bond will break, they are also related to the presence of hydrogen bonding in the case of BCPs between non-bonded atoms. The QTAIM analysis was carried out using the Avogadro2 software package.

The QTAIM analysis was carried out on the trans-Stilbene and Shi catalyst RR2 and SS3 (the most stable RR and most stable SS) transition states. For the RR2 transition state it reveals that there are 3 interactions between the Oxygen atoms on the Shi catalyst and the hydrogen atoms on the stilbene, there are also 2 H-C and 2 H-H interactions. The non-bonded O-H BCPs are indicative of hydrogen bonding and may account for some of the stabilisation of the transition state.

By comparison, although the SS3 transition state shows 3 non-bonded O-H hydrogen bonding interactions, the same as for the RR2 transition state, there is only one non-bonded C-H BCP. This supports the finding of the NCI analysis that there are fewer favourable non-bonding interactions for the SS3 state when compared with the RR2 state. Together these both suggest that the RR2 is the favoured transition state.

New Candidate for Investigation

A new candidate for investigation could be 2-phenyl-3-p-tolyl-oxirane which has an optical rotatory power of -380 degrees, the alkene (4-methyl-stilbene) is available for purchase as of 21/03/2014 from TCI Europe.

Since the reported optical rotatory power is so strong it should be easy to identify which enantiomer has been produced using the calculation and also due to the literature on the compound being so dated, it is unlikely to have been checked against a calculation, meaning that the assignment may well be incorrect. It would also be interesting to comment on the effect of the addition of the methyl group by comparing the results with that of the stilbene investigated above.