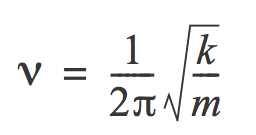Rep:Mod:DDB2716
NH3 molecule
The NH3 molecule has been modelled and optimised using the Gaussian software.
| Optimised NH3 molecule | ||
|---|---|---|
| ||
| Summary | ||
| Calculation Type | FREQ | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d,p) | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | -56.55776873 a.u. | |
| RMS Gradient Norm | 0.00000485 a.u. | |
| Imaginary Freq | 0 | |
| Dipole Moment | 1.8466 | |
| Point Group | C3V | |
Further investigations have shown that the N-H bond distance is 1.01798 Angstrom , while the H-N-H bond angle is 105.74115 degrees .
A look in the Item table, found in the .log file, has shown that the molecule has been optimised.
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986269D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The optimisation file is liked to here .
3D model of the optimised NH3 molecule |
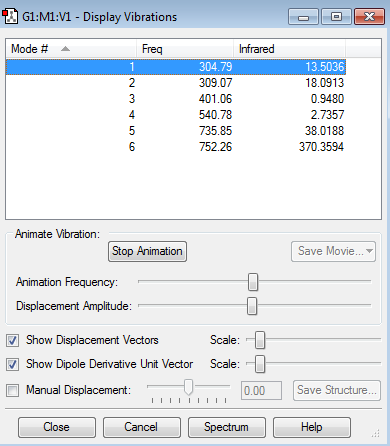
The vibration modes of NH3 have also been investigated with Gaussian, the results being shown in the window below:
How many modes do you expect from the 3N-6 rule?
NH3 has 4 atoms, so the 3N-6 rule would give 3*4-6=6 vibrations mode, which is indeed the number of vibrations modes found by Gaussian.
Which modes are degenerate (ie have the same energy)?
Modes 2 and 3 have the same frequency (1693.95), and so do modes 5 and 6 (3589.82). Therefore, they are degenerate.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?
The first 3 modes (numbers 1,2,3) are "bending" vibrations, while the last 3 modes (numbers 4,5,6) are "bond stretch" vibrations.
Which mode is highly symmetric?
Mode 4 is highly symmetric, as it is the symmetric bond stretch.
One mode is known as the "umbrella" mode, which one is this?
The "umbrella" mode is mode 1 .
How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
The Gaussian software gives 4 distinct intensity values for the vibrations of NH3 (with relative intensities of 145.3814 : 13.5533 : 1.0608 : 0.2711). However, the last 2 relative intensities are very small, so the bands for those frequencies are very small and difficult to spot. Therefore, even if there are four different frequencies for vibrations in ammonia, the experimental spectrum is expected to show only 2 bands.
The literature values are close to those determined by Gaussian: 968.32 cm-1, 1627.26 cm-1, 3337.18 cm-1, 3443.94 cm-1. [1] .
The charge distribution of the NH3 molecule has also been investigated using the Gaussian software. The expected outcome would be to have the negative charge on the nitrogen atom and the positive charges on the hydrogen atoms because nitrogen is more electronegative than hydrogen. The experimental data confirms the theoretical expectations, as the charge on nitrogen is -1.125, whereas the charge on each hydrogen atom is +0.375.
N2 molecule
The N2 molecule has been modelled and optimised using the Gaussian software.
| Optimised N2 molecule | ||
|---|---|---|
| ||
| Summary | ||
| Calculation Type | FREQ | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d,p) | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | -109.52412868 a.u. | |
| RMS Gradient Norm | 0.00000060 a.u. | |
| Imaginary Freq | 0 | |
| Dipole Moment | 0.0000 | |
| Point Group | D∞h | |
A look in the Item table, found in the .log file, has shown that the molecule has been optimised.
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400954D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The optimisation file is liked to here .
H2 molecule
The H2 molecule has been modelled and optimised using the Gaussian software.
| Optimised H2 molecule | ||
|---|---|---|
| ||
| Summary | ||
| Calculation Type | FREQ | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d,p) | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | -1.17853936 a.u. | |
| RMS Gradient Norm | 0.00000017 a.u. | |
| Imaginary Freq | 0 | |
| Dipole Moment | 0.0000 | |
| Point Group | D∞h | |
A look in the Item table, found in the .log file, has shown that the molecule has been optimised.
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The optimisation file is liked to here .
Haber-Born cycle for NH3 formation
The reaction for the formation of NH3 from elements is:
N2 + 3H2 -> 2NH3
To calculate the energy for converting hydrogen and nitrogen into ammonia, the following data has been used:
E(NH3) = -56.55776873 a.u.
2*E(NH3) = -113.11553746 a.u.
E(N2) = -109.52412868 a.u.
E(H2) = -1.17853936 a.u.
3*E(H2) = -3.53561808 a.u.
ΔE =2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557907 a.u. = -146.47848285 kJ/mol
Using the data provided by the Gaussian optimisations of NH3, N2, H2, the reaction energy was found to be -146.47848285 kJ/mol. The negative sign of it indicates that the product is more stable than the reactants. This value is significantly different from literature data (−46.11 kj/mol). [2]
Project molecule - ClF3
ClF3 is a molecule that shows interesting structural characteristics. VSEPR theory predicts a trigonal bipyramidal pseudo structure, with the T-shaped structure being the actual one. The lone pairs are expected to adopt equatorial position, so that the repulsions would be minimal.
The ClF3 molecule has been modelled and optimised using the Gaussian software. The results were then compared with literature.
| Optimised ClF3 molecule | ||
|---|---|---|
| ||
| Summary | ||
| Calculation Type | FREQ | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d,p) | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | -759.46531688 a.u. | |
| RMS Gradient Norm | 0.00002465 a.u. | |
| Imaginary Freq | 0 | |
| Dipole Moment | 0.8386 Debye | |
| Point Group | C2v | |
Item Value Threshold Converged?
Maximum Force 0.000050 0.000450 YES
RMS Force 0.000028 0.000300 YES
Maximum Displacement 0.000204 0.001800 YES
RMS Displacement 0.000134 0.001200 YES
Predicted change in Energy=-1.250230D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.7286 -DE/DX = 0.0 !
! R2 R(1,3) 1.6514 -DE/DX = 0.0 !
! R3 R(1,4) 1.7286 -DE/DX = 0.0 !
! A1 A(2,1,3) 87.1404 -DE/DX = 0.0 !
! A2 A(3,1,4) 87.1404 -DE/DX = 0.0 !
! A3 L(2,1,4,3,-1) 174.2807 -DE/DX = 0.0 !
! A4 L(2,1,4,3,-2) 180.0 -DE/DX = 0.0 !
! D1 D(2,1,3,4) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The optimisation file is liked to here .
3D model of the optimised ClF3 molecule |
The bond lengths and angles have been investigated after the optimisation had been performed. It was found that ClF3 has 2 different types of Cl-F bonds: 1.72863 (bonds 1-2 and 1-4) and 1.65143(bond 1-3). This molecule presents 2 different angle values as well. The angles between atoms 2-1-3 and 3-1-4 are 87.14037 degrees, while the angle between atoms 2-1-4 is 174.28073 degrees.
The values given by literature are 1.598 Angstrom for the short bond and 1.698 Angstrom for the 2 long bonds. The angle defined by the 2-1-3 and 3-1-4 notations is found to be 87°29′, experimentally. [3]
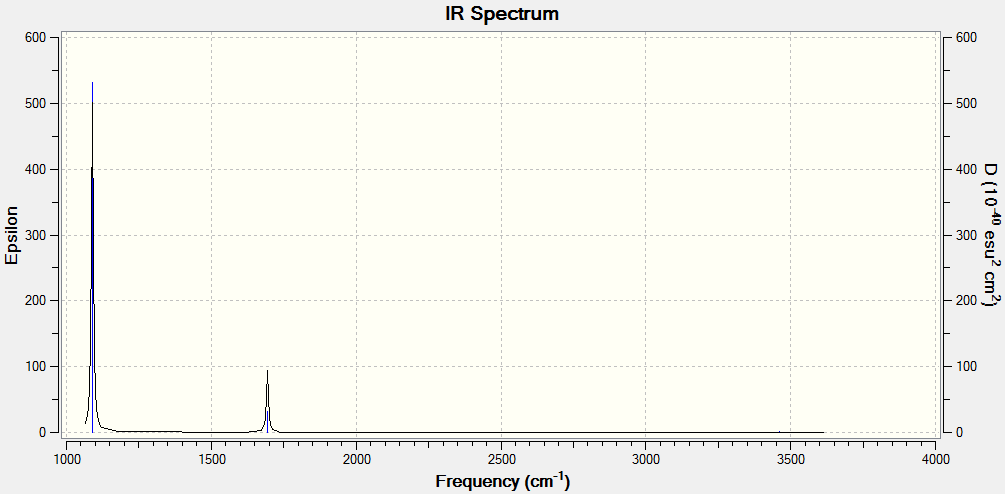
The vibration modes of ClF3 have also been investigated with Gaussian, the results being shown in the window below:
As expected from the 3N-6 rule for non-linear molecules, ClF3 has 6 modes of vibrations. None of them are degenerate, as all the frequency values listed by Gaussian are different. The first three vibrations are for bending modes, while the last three ones are for bond stretches. The first vibration is a deformation (in-plane bend), the second one is the wagging of Cl atom, while the third one is the rocking of Cl atom. The fourth vibration mode is the symmetric axial stretch, the fifth is the equatorial stretch, while the last one is the asymmetric axial stretch. All 6 modes are IR active because all of them give rise to a change in the dipole moment of the molecule.
Literature cites values of 752.1, 529.3, and 328 (a1), 702 and 442 (b1), and 328 (b2)cm-1. [4]
The spectrum
ClF3 is an interesting molecule in term of charge distribution because it is one of the few examples where chlorine has a positive charge. Chlorine is a very electronegative atom, but fluorine is even more so. Therefore, the electrons are drawn much more towards fluorine. Thus, overall, chlorine has a charge of +1.048, while each fluorine atom has a charge of -0.394.
Molecular Orbitals of ClF3
The frst 30 molecular orbitals of ClF3 have been modeled using Gaussian. Out of them, the following significant 6 have been investigated further:
The first molecular orbital, arising from the in-phase combination of the 1s orbitals of F and Cl, is so deep in energy (-101.79317 ) that Gaussian cannot show it. Therefore, the 1s orbitals are too close to the nuclei of the atoms and have a significantly low contribution to the overall bonding of the molecule.
The 9th molecular orbital is a bonding one, formed between 2s orbitals of all F atoms and of the Cl atom. This molecular orbital is much higher in energy (-1.28161 ), so the graphical representation is clearly visible now. It is a σ molecular orbital.
The 12th molecular orbital is an anti-bonding one, arising from an out-of-phase combination of the 2s orbitals of all atoms involved in the molecule. Therefore, it is a σ* molecular orbital. Its energy is -0.89010.
The 13th orbital is an overall bonding one. The orbitals involved are a p orbital of Cl and p orbitals from each of the F atoms. The 2 Cl-F bonds which form the 174.28073 angle are the same, formed by π interactions between the p orbitals on Cl and the 2 F atoms, while the other Cl-F bond is formed by a linear combination of p orbitals.
The 19th molecular orbital of ClF3 is showing an antibonding relationship between the F-Cl-F that form the 174.28073 angle. There is a π* interaction between the p orbitals of Cl and the 2 F. However, the other F doesn't contribute to this π* molecular orbital, so it is in a nonbonding relationship with the central Cl.
The 22nd molecular orbital is the last occupied one, so it is the HOMO. It is an anti-bonding orbital with respect to the interactions between Cl and F, as can be seen from the snapshot. However, all F atoms are in phase, so they have a bonding interaction. The atomic orbitals involved in its formation are the p orbitals from Cl and F atoms. Its energy is -0.33458.
The 23rd molecular orbital is the LUMO. It is an overall antibonding orbital, arising from out-of-phase interactions between a p orbital of Cl and 3 p orbitals from the 3 F atoms. Its energy is -0.15006.
Further investigations - BrF3
Furthermore, BrF3 has been investigated using Gaussian in order to make an accurate comparison between it and ClF3. Both molecules adopt the same structure (T-shaped). However, the exact parameters differ, as can be seen from the optimised Gaussian job.
| Summary | ||
|---|---|---|
| Calculation Type | FREQ | |
| Calculation Method | RB3LYP | |
| Basis Set | 6-31G(d,p) | |
| Charge | 0 | |
| Spin | Singlet | |
| E(RB3LYP) | -2871.04029135 a.u. | |
| RMS Gradient Norm | 0.00004698 a.u. | |
| Imaginary Freq | 0 | |
| Dipole Moment | 1.353 Debye | |
| Point Group | C2v | |
Item Value Threshold Converged?
Maximum Force 0.000117 0.000450 YES
RMS Force 0.000044 0.000300 YES
Maximum Displacement 0.000357 0.001800 YES
RMS Displacement 0.000162 0.001200 YES
Predicted change in Energy=-3.147111D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.7671 -DE/DX = -0.0001 !
! R2 R(1,3) 1.8395 -DE/DX = 0.0 !
! R3 R(1,4) 1.8395 -DE/DX = 0.0 !
! A1 A(2,1,3) 86.2218 -DE/DX = 0.0 !
! A2 A(2,1,4) 86.2218 -DE/DX = 0.0 !
! A3 L(3,1,4,2,-1) 172.4436 -DE/DX = 0.0 !
! A4 L(3,1,4,2,-2) 180.0 -DE/DX = 0.0 !
! D1 D(1,2,4,3) 0.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
The optimisation file is liked to here.
The short Cl-F bond is 1.6514 Angstrom, while the short Br-F was estimated to be 1.7671 Angstrom. The other two Cl-F bonds are 1.7286 Angstrom, while the long Br-F bonds are 1.8395.
Overall, all the bonds in BrF3 are longer than those in ClF3. This result is in accordance with the theoretical expectations. Br is more voluminous than Cl, therefore it is expected that a Br-F bond should be longer than a Cl-F one, due to a less effective orbital overlap between the large Br and the small F. Meanwhile, the size of Cl is closer to the one of F, so the bond is shorter.
The same rationalisation can be applied when looking at the angle values as well. The F-Br-F angles are all smaller than the F-Cl-F ones, suggesting that the two lone pairs of Br are in bigger orbitals than those of Cl, which is also confirmed by theory (chlorine's electronic configuration is [Ne] 3s2 3p5, while bromine's electronic configuration is [Ar] 3d10 4s2 4p5, so bromine's valence electrons are in bigger orbitals than chlorine's).
In comparison with ClF3, the central atom in BrF3 has a smaller positive charge (1.022 compared to 1.048). This can be easily explained, as the electronegativity of Br is smaller than that of Cl, so the F atom attracts the bond electrons better in BrF3 than in ClF3.
Also, the dipole moment of BrF3 is higher than that of ClF3, because the difference in electronegativity is bigger in the first molecule than in the latter.
The vibrations of BrF3 have been investigated using Gaussian, in order to compare them as well with those of ClF3.
It is known that the anharmonic oscillator obeys the following formula:
Therefore, the frequency is inversely proportional to the reduced mass of the system. As expected from theoretical knowledge, the vibrations in BrF3 have a lower frequency because Br is heavier than Cl.
References
- ↑ http://iopscience.iop.org/article/10.1088/0022-3700/5/2/038/pdf
- ↑ Atkins' Physical Chemistry (10th Edition), Peter Atkins and Julio de Paula, Published by Oxford, 2014
- ↑ http://aip.scitation.org/doi/10.1063/1.1698976
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedClF3 vibrations - ↑ https://d32ogoqmya1dw8.cloudfront.net/images/NAGTWorkshops/mineralogy/mineral_physics/anharmonic_oscillator_1332484707.jpg
Cite error: <ref> tag with name "ClF3_vibrations" defined in <references> is not used in prior text.