Rep:Mod:DC3415

NH₃ molecule

A range of properties of the molecule ammonia, NH₃ including N-H bond length, H-N-H bond angles and molecule energy were calculated using the program Gaussian.

Calculation method, basis set, point group and final energy of ammonia

The calculation method used to optimize the structure of ammonia along with the basis set used and the calculated final energy of the molecule, E(RB3LYP), are shown in a summary table below together with the point group of the molecule.

NH₃ Symmary table

parameter	value
calculation method	RB3LYP
basis set	6-31G(d,p)
E(RB3LYP)	-56.55776873 a.u.
RMS gradient norm	0.00000485 a.u.
Point Group	C3V

N-H bond length and H-N-H bond angle

After optimisation of the molecule using the above mentioned optimisation settings, the N-H bond length was found to be 1.01798 ‎Å and the H-N-H bond angle was found to be 105.741^o.

Item table from Gaussian log file

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
 

The fact that all the items have converged, suggests that the optimisation was successful.

Dynamic image

A dynamic image of the ammonia molecule is found below:

.log file here

ammonia molecule

Bond Vibrations

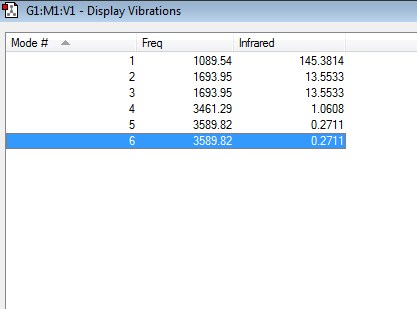
A screenshot of the different vibrational modes of ammonia is shown below:

Using the 3N-6 rule for triatomic molecules the number of predicted vibrational modes is 6, since N=4. Vibrational modes 2 and 3 are degenerate since they have the same frequency, 1693.95 cm^-1 and the same infrared intensity, 13.5533. Also vibrational modes 5 and 6 are degenerate for the same above mentioned reasons. However these vibrations occur at a higher frequency, 3589.82 cm^-1 and have a lower intensity, 0.2711. Bending vibrations are often observed at lower frequencies than stretches. Vibrational modes 1, 2 and 3 are caused by bending of the N-H bonds whereas vibrational modes 4, 5 and 6 are caused by stretching of the N-H bonds. Vibration number 4 is a highly symmetric stretch as all the N-H bonds stretch equally resulting in no net change in the dipole moment. Vibrational mode 1 is known as an 'umbrella bend' since the N-H bonds bend resembling the motion of the opening of an umbrella. 2 bands are expected to be seen in a spectrum of gaseous ammonia since vibrations 2 and 3 are degenerate, and so are 5 and 6 so each pair will only produce one band. However, due to their low intensity, vibrational modes 5 and 6 will not be visible on the spectrum. A band will be created by the umbrella bend. Vibrational mode number 4, that is the symmetric stretch is not expected to appear on the spectrum since the stretch do not cause a change in the dipole moment of the molecule.

Charge distribution values

Analysis of charge distribution on the NH₃ molecule showed that the charge on each hydrogen atom is +0.357 whereas the charge on the Nitrogen molecule is -1.125. These values are what was expected since nitrogen is more electronegative than hydrogen, hence it will attract electrons more, resulting in a partial negative charge on the nitrogen and partial positive charges on each hydrogen.

N₂ and H₂ molecules

A similar method to ammonia was used to optimise N₂ and H₂ molecules on Gaussian.

N₂ molecule

The calculation method used to optimise the N₂ molecule, the basis set and final energy, E(RB3LYP), gradient norm value and point group are summarised in the table below. N-N triple bond length was found to be 1.10550 ‎Å and the bond angle 180^o.

N₂ Symmary table

parameter	value
calculation method	RB3LYP
basis set	6-31G(d,p)
E(RB3LYP)	-109.52416848 a.u.
RMS gradient norm	0.00000365 a.u.
Point Group	D∞h

The ground state energy of nitrogen was found in another experiment to be -108.9956 a.u. that is similar to the value calculated by Gaussian.

The "item" table from the optimisation .log file of N₂ is shown below:

         Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000002     0.001800     YES
 RMS     Displacement     0.000003     0.001200     YES

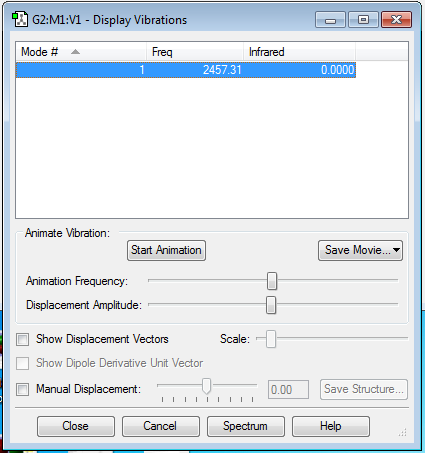
Frequency vibration analysis shows that there is only one vibrational mode that is a symmetric stretch at 2457.31 cm^-1. It is expected that there will only be one vibrational mode due to the fact that the molecule is linear. Charge distribution analysis showed that there is no charge on any of the atoms since the molecule is homodinuclear.

.log file here

Nitrogen molecule

Note: Rotate the dynamic image to view the whole molecule.

H₂ molecule

The calculation method used to optimise the H₂ molecule, basis set and final energy, E(RB3LYP), the RMS gradient norm value and the point group of the molecule are summarised in the table found below. H-H bond length was found to be 0.74279 ‎Å and the bond angle 180^o.

H₂ Symmary table

parameter	value
calculation method	RB3LYP
basis set	6-31G(d,p)
E(RB3LYP)	-1.17853936 a.u.
RMS gradient norm	0.00000204 a.u.
Point Group	D∞h

This value is similar to the values obtained in other experiments that used different methods. The values obtained in these experiments ranged from -1.163 a.u. to -1.175 a.u.

The "item" table from the optimisation .log file of H₂ is shown below:

Hydrogen molecule item table

Item	Value	Threshold	Converged?
Maximum Force	0.000004	0.000450	YES
RMS Force	0.000004	0.000300	YES
Maximum Displacement	0.000005	0.001800	YES
RMS Displacement	0.000007	0.001200	YES

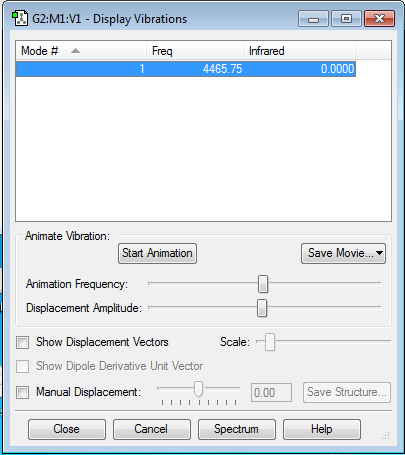
Frequency vibration analysis shows that there is only one vibrational mode that is a symmetric stretch at 4465.75 cm^-1. It is expected that there will only be one vibrational mode due to the fact that the molecule is linear. Charge distribution analysis showed that there is no charge on any of the atoms since the molecule is homodinuclear.

.log file here

Hydrogen molecule

Note: Rotate the dynamic image to view the whole molecule.

Energy values and calculation of reaction energy

E(NH₃)= -56.55776873 a.u.

2*E(NH₃)= -113.11553746 a.u.

E(N₂) = -109.52416848 a.u.

E(H₂) = -1.17853936 a.u.

3*E(H₂) = -3.53561808 a.u.

ΔE = 2*E(NH₃)-[E(N₂)+3*E(H₂)]= -0.0557509 a.u.

To convert a.u. to KJ*mol^-1 ΔE is multiplied by 2625.5. -0.0557509*2625.5= -146.37 KJ*mol^-1.

Therefore, the calculated energy value for the conversion of N₂ and H₂ to NH₃ is -146.37 KJ*mol^-1. The negative sign indicates that the reaction is exothermic and therefore the product is energetically more stable than the reactant gases. The calculated enthalpy change of the reaction is much higher than the actual value, that is -92 KJ*mol^-1. This is because the calculation conditions used by Gaussian are different than normal experimental calculations that affect the enthalpy change value obtained.

Cl₂ molecule

Cl₂ summary

Using a similar procedure to the one used to analyse the molecules above, the Cl₂ molecule was also optimised and analysed on Gaussian.

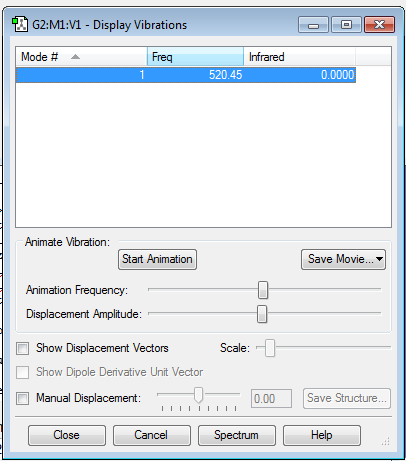
The calculation method used for optimisation was RB3LYP with a basis set of 6-31G(d,p). The final energy of the molecule, E(RB3LYP), was calculated to be -920.34987887 a.u. with RMS gradient norm of 0.00000557 a.u. The point group of the molecule is D_∞h since the molecule is linear. The Cl-Cl bond angle is 180^o and the bond length is 2.04164 ‎Å. Frequency analysis of the Cl₂ molecule showed a single stretch vibration at 520.45 cm^-1 as expected by a heavy homodinuclear molecule. Infra red intensity is 0 since symmetric stretches do not induce changes in the dipole moment of the molecule. Charge distribution analysis showed 0 charge on both Cl atoms since there is equal distribution of charge between the same atoms because they have the same electronegativity.

The "Item" table from the .log file generated, the vibrational mode and the link to the .log file are found below:

Chlorine molecule item table

Item	Value	Threshold	Converged?
Maximum Force	0.000010	0.000450	YES
RMS Force	0.000010	0.000300	YES
Maximum Displacement	0.000027	0.001800	YES
RMS Displacement	0.000038	0.001200	YES

.log file here

Chlorine molecule

Note: Rotate the dynamic image to view the whole molecule.

Molecular orbital analysis

Molecular orbital analysis of the Cl₂ molecule revealed some atomic orbital overlaps that are worth mentioning:

This is the 4σ_g molecular orbital that results from the in-phase overlap of the 3s orbitals of each Cl atom to form a bonding orbital. This a low energy orbital and is much lower in energy than the orbitals in the LUMO/HOMO region. This molecular orbital is occupied by 2 electrons. This orbital is stabilised even further as a result of mixing with the 5σ_g molecular orbital.

This is the 4σ^*_u molecular orbital that results from the out-of-phase overlap of the 3s atomic orbitals of each Cl atom to form the antibonding orbital. This orbital is also occupied by two electrons. The lack of electron density at the centre of the bond indicates the presence of a nodal plane which results in an increase in the molecular orbital energy.

The above image corresponds to the 5σ_g molecular orbital that results from the in-phase overlap of the 3p_x atomic orbitals of each Cl atom to form a bonding orbital. The 3p_x atomic orbitals overlap along the x-axis and there is electron density between the bonding atoms hence it is a bonding molecular orbital. This molecular orbital was expected to be higher in energy than the corresponding orbitals formed by 3p_y-3p_y and 3p_z-3p_z overlaps as a result of it mixing with the σ_g molecular orbital formed by 3s-3s overlap. However this in not the case most probably due to inaccuracies in Gaussian NBO orbital calculation method.

This image corresponds to the 5σ^*_u molecular orbital that results from the out-of-phase overlap of the 3p_x atomic orbitals of each Cl atom to form an antibonding orbital. This overlap results in the formation of 3 nodes between the two nuclei hence it is a very high energy orbital. This orbital is the lowest unoccupied molecular orbital (LUMO) of the chlorine molecule.

The last image corresponds to the 2π^*_u molecular orbital that results from the out-of-phase overlap of the 3p_y atomic orbitals of each Cl atom to form an anti-bonding orbital. This is an occupied orbital as is the 2π^*_u formed by the overlap of the 3p_z atomic orbitals of chlorine. These two molecular orbitals are degenerate and both hold 2 electrons. They are the highest occupied molecular orbitals (HOMOs) of the chlorine molecule.