Rep:Mod:DAAO phys
Module 3: Transition States & Reactivity
Introduction
This report cites and discusses the results from a set of computational experiments involving the Cope rearrangement. This includes characterising the transition structures on the potential energy surfaces of this rearrangement. This builds both on previous work performed during second year physical chemistry laboratory course at Imperial College London in 2009 and the more recent computational laboratory course in 2010. Here, using methods based on molecular orbitals, one will calculate what the transition structures of this rearrangement will look like as well as reaction paths and barrier heights.
The Cope Rearrangement Tutorial
This section focuses on the Cope rearrangement of 1,5-hexadiene in order to show how chemical reactivity problems can be studied. This will involve locating the low-energy minima and transition structures on the 1,5-hexadiene potential energy surface and hence determining the preferred reaction mechanism. After some controversy, it is generally believed that this [3,3]-sigamatropic shift rearrangement occurs via a concerted mechanism with either a ‘chair’ or ‘boat’ transition state. [1]

Optimising the Reactants and Products
Using the program GaussView 3.09, a molecule of 1,5-hexadiene was created so that its four central carbon atoms approximately had an anti-periplanar arrangement. This structure was tidied up by using the clean function. The structure was then optimised at the HF/3-21G level of theory. This means that the optimisation calculation using Gaussian was done using the the Hartree Fock method and the 3-21G basis set. The calculation summary did not show the point group of the structure and therefore was symmetrised which then showed the point group. This process was then repeated for 1,5-hexadiene with the four central carbon atoms in a gauche arrangement. These optimised structures were then compared to those given in a table in Appendix 1 and identified. The results obtained are shown below.
| Anti Conformer | Gauche Conformer | |
|---|---|---|
| Optimised Structure | 
|
File:DAAO react gauche.jpg |
| jmol | ||
| Calculation Summary | File:DAAO anti calc summary.png | File:DAAO gauche calc summary.png |
| Point Group | Ci | C2 |
| Structure in Appendix 1 Table | anti2 | gauche4 |
The above shows the anti conformer to be lower in energy. This could be due to there being less torsional strain present in the molecule. In order to achieve lower energy conformers, both the anti and gauche structures shown above were manipulated (by changing the dihedral angles) to reduce steric strain. These geometries were then optimised and indentified with reference to the table in Appendix 1. The results are shown below.
| Anti Conformer | Gauche Conformer | |
|---|---|---|
| Optimised Structure | File:DAAO React 2nd anti.jpg | 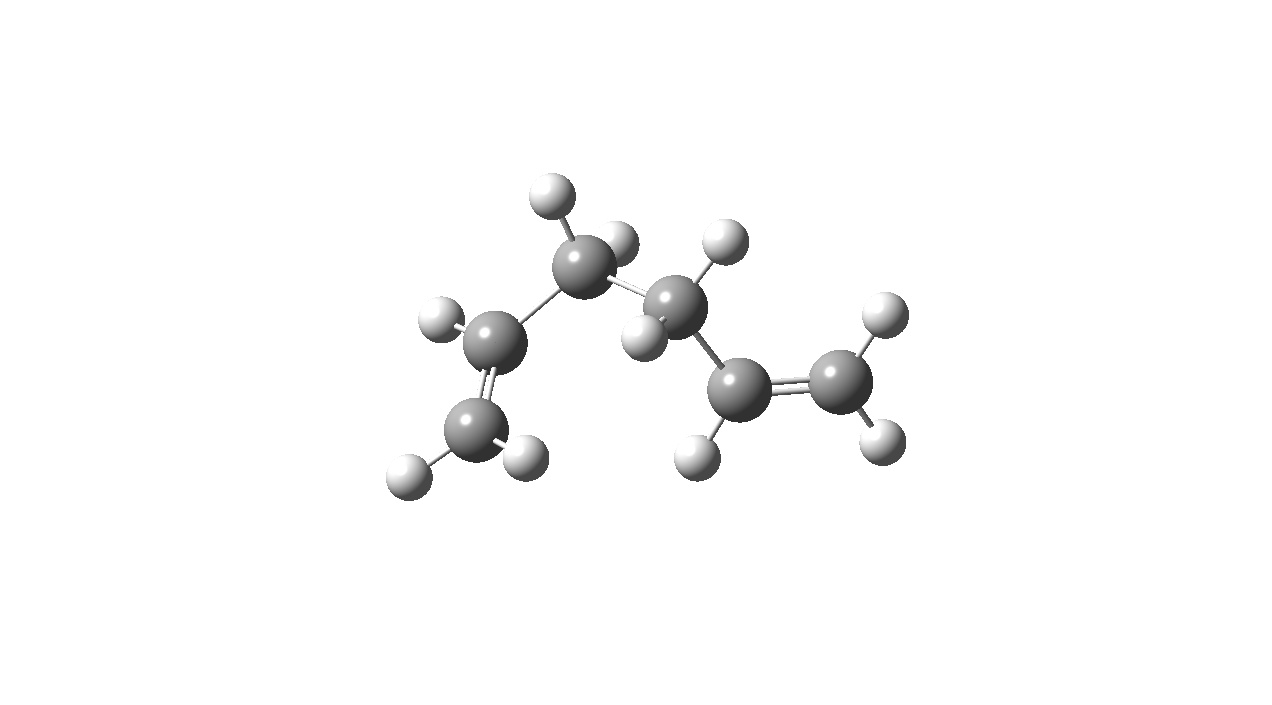
|
| jmol | ||
| Calculation Summary | 
|
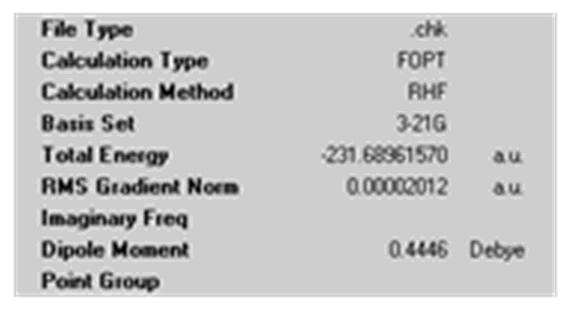
|
| Point Group | Ci | C1 |
| Structure in Appendix 1 Table | anti1 | gauche5 |
From the above we can see that manipulating the anti conformer lead to a lower energy geomtery yet in the case of the gauche isomer manipulation lead to a higher energy conformer. This suggests the possiblity that there is a favorable interaction present involving the carbon-carbon double bond and the vincinal proton in the gauche conformer that perhaps compensates for the additional torsional strain compared to the anti isomer.
All of the structures drawn agree with the values given in Appendix 1 to 5 decimal places.
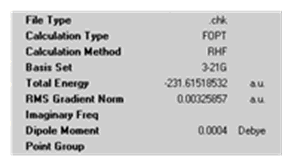
The anti 1,5-hexadiene with Ci symmetry was then reoptimised at the higher level of theory of B3LYP/6-31G*.
| HF/3-21G | B3LYP/6-31G* | |
|---|---|---|
| Optimised Structure | 
|

|
| jmol | ||
| Calculation Summary | File:DAAO anti calc summary.png | File:DAAO 1st anti reopt calc summary.png |
| Point Group | Ci | Ci |
Comparing the different levels of theory used for the optimisation the following was noted:


| Bond | HF/3-21G Optimised Structure Bond Distance/ Å | B3LYP/6-31G* Optimised Structure Bond Distance/ Å | Difference in Bond Distances between Methods/ Å |
|---|---|---|---|
| C1=C2 | 1.32 | 1.33 | 0.01 |
| C2-C6 | 1.51 | 1.50 | 0.01 |
| C6-C9 | 1.55 | 1.55 | 0.0 |
| C9-C12 | 1.51 | 1.50 | 0.01 |
| C12=C13 | 1.32 | 1.33 | 0.01 |
| Dihedral Angle | HF/3-21G Optimised Structure Dihedral Angle/ ⁰ | B3LYP/6-31G* Optimised Structure Dihedral Angle/ ⁰ | Difference in Dihedral Angle between Methods/ ⁰ |
|---|---|---|---|
| C1-C2-C6-C9 | 115 | 119 | 4 |
| C2-C6-C9-C12 | 180 | 113 | 67 |
| C6-C9-C12-C13 | 115 | 119 | 4 |
| Angle | HF/3-21G Optimised Structure Angle/ ⁰ | B3LYP/6-31G* Optimised Structure Angle/ ⁰ | Difference in Angle between Methods/ ⁰ |
|---|---|---|---|
| C1-C2-C6 | 125 | 125 | 0 |
| C2-C6-C9 | 111 | 113 | 2 |
| C6-C9-C12 | 111 | 113 | 2 |
| C9-C12-13 | 125 | 125 | 0 |
Energies obtained between the methods cannot be compared as different basis sets were used. Reoptimisation using a better basis set showed very little difference in bond lengths between the two structures. Bond lengths are either identical or slightly longer for the structure optimised to a higher level of theory. The greatest difference in geometry between the two optimised structures is found when one looks at their dihedral angles. As there is such a small difference in bond lengths between the two optimised structures comparison to literature is futile. However, this small difference between the structure optimised at different levels of theory suggests that a smaller basis set sometimes is appropriate for calcualtions and a larger basis set is unnecessary especially when one takes into account the increase time involved in calculations.
Vibrational Analysis
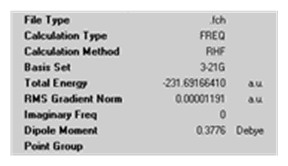
It can be confirmed that the B3LYP/6-31G* optimisation was successful by vibrational analysis. Frequency calculations were performed using the same method and basis set as used for the optimisation (B3LYP/6-31G*).

There are no imaginary frequencies i.e. all vibrational frequencies are positive so it is known that optimisation was successful and a transition structure was not achieved.
The output file provides details such as those shown below which will enable the activation energy of the Cope rearrangement to be calculated later in this report.
File:DAAO 1st anti reopt thermo.png
Optimising the 'Chair' and 'Boat' Transition Structures
Here, both the ‘chair’ and ‘boat’ transition structures will be optimised by computing the force constants at the beginning of the calculation, using the redundant coordinate editor and QST2 method. The reaction coordinate will be visualised, the IRC run and the activation energies for the Cope rearrangement by both the ‘chair and ‘boat transition structures.
Optimising an Allyl Fragment
An allyl fragment (CH2CHCH2) was created using GaussView 3.09 and optimised at the HF/3-21G level of theory.
| Optimised Structure | 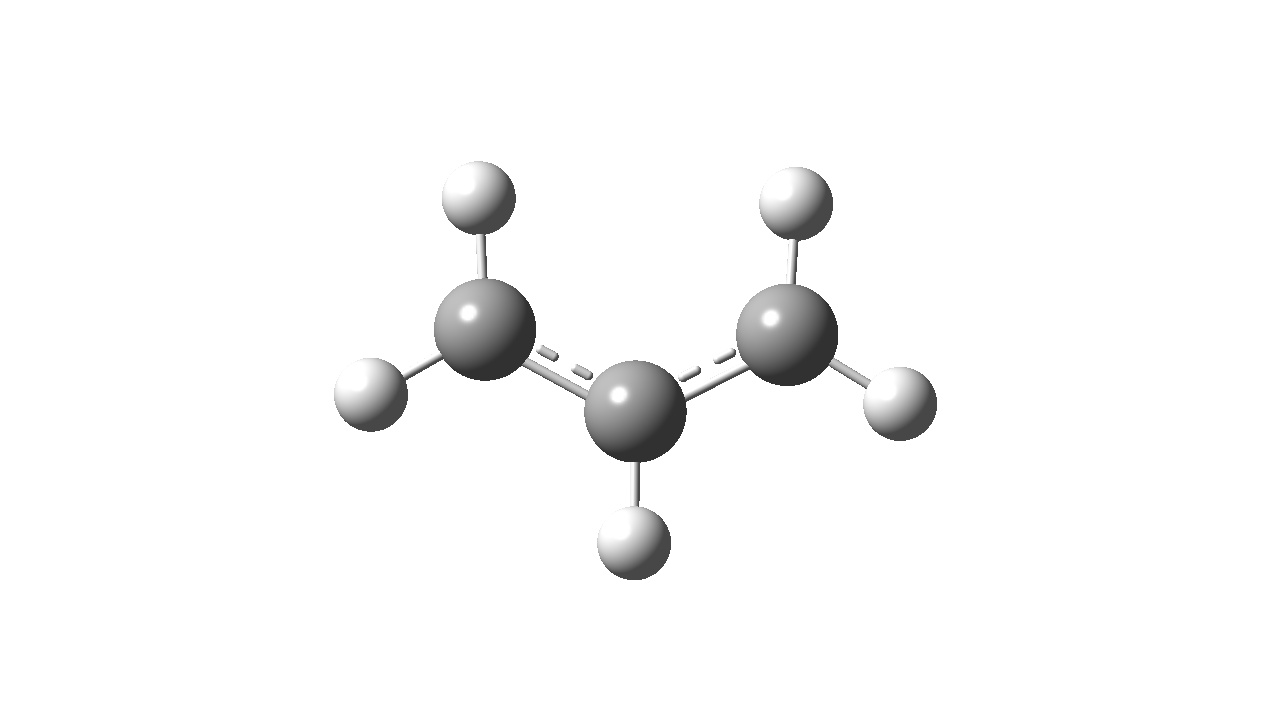
|
| jmol | |
| Calculation Summary | 
|
File:DAAO allyl converged output.png
Optimising the 'Chair' Transition Structure
Two of these fragments were oriented at shown below and optimised with Gaussian by selecting Opt+Freq as the job type, ‘Optimisation to a TS (Berny)’, force constants to be calculated once, and HF/3-21G as the level of theory. The keywords Opt=NoEigen were also added to prevent the calculation from crashing.


After optimisation the distance between the terminal carbons decreased from 2.13 and 2.07 Å to 2.02 Å for both distances. The job was successful as vibrational analysis shows that an imaginary frequency of -818 cm-1 was obtained. This vibrational mode corresponds to the Cope rearrangement and shows two terminal carbon atoms approach each other to form a bond while the opposite two carbons atoms move apart as the C-C bond breaks.
File:DAAO chair berny freq calc summary.png

The guess ‘chair’ transition structure was then optimised using the frozen coordinate method. This was done in two steps the first of which involved fixing the distance between the terminal carbons forming/ breaking a bond during the rearrangement to 2.2 Å and using Gaussian to perform the optimisation.

This optimised structure looks similar to that achieved after optimisation to a TS (Berny) but the C-C bond length is 2.2 Å rather than 2.02 Å.
The second step of this optimisation method involved optimising to a TS (Berny) again but this time the force constants were not calculated.
File:DAAO chair ts d calc summary.png
The optimised structures from both methods have the same bond lengths and angles. Both structures have a carbon-carbon bond length of 1.39 Å, a distance of 2.02 and 2.88 Å between the terminal and central carbons of the transition structure respectively. The frozen coordinate method is more time consuming as it requires two calculations. However, this method yielded a slightly lower energy 'chair' transition structure by 2.1 x 10-7 a.u.
Optimising the 'Boat' Transition Structure
The ‘boat’ transition structure was then optimised using the QST2 method. The method involves both the reactants and products and tries to interpolate the two to find the transition structure. Using the anti2 stucture previously optimised, it was first necessary to ensure that the reactants and products were labelled in the same way.

After submitting the ‘Opt+Freq’ job to Gaussian selecting TS(QST2) and the same method and basis set as previously used it was seen that the job had failed. This is due to the possible rotation about the central bonds not being considered. From this, we know that the QST2 method will not locate the transition structure starting from the above structures for the reactant and product.
However, by using the original input file and modifying the reactant and product starting configurations one can locate the boat transitions structure.
File:Qst2 rearranged react.jpg
File:DAAO rearranged calc summary.png
Looking the output file, it can be seen that there is one imaginary frequency at -840 cm-1. This confirms that a transition state was obtained. This corresponds to the cope rearrangement via the ‘boat’ transition structure.



Intrinsic Reaction Coordinate (IRC) Method
It is difficult to tell which conformer of 1,5-hexadiene is connected to the optimised transtion structures found above. The Intrinsic Reaction Coordinate (IRC) method allows us to predict which conformer of 1,5-hexadiene will be obtained from the ‘chair’ and ‘boat’ transition structures. Gaussian is used in this method and enables us to follow the minimum energy path with small changes in the geometry in the direction where the gradient of the potential energy surface is steepest.
Intrinsic Reaction Coordinate (IRC) Method for 'Chair' Transition State
The checkpoint file for the chair structure optimised to a TS (Berny) was opened. Using Gaussian, the job type IRC was chosen with the reaction coordinate computed only in the forward direction as it is symmetrical. The force constant was calculated once, IRCMax option was left unchecked and the number of points along the IRC was increased from the default 6 to 50.
After the job had finished, it was seen from the following that a minimum geometry was not reached. The IRC reaction coordinate vs RMS gradient is the very useful. It shows that the the gradient had not yet reached zero and so a minimum on the PES had not been found. The struture obtained did not correspond to any of the low energy conformers of 1,5-hexadiene given in Appendix 1.


In order to achieve the geometry minimum 3 options were suggested. Each approach will now be discussed.
Approach 1: Run a Normal Minimisation on Struture Obtained After 50 Iterations
This approach is the fastest of the three suggested however, it can lead to obtaining the wrong minimum if the geometry is not close enough to a local minimum. The following results were obtained.
File:DAAO IRC app1 calc summary.png
File:DAAO IRC app1 converged.png

The structure obtained from this method has C2 symmetry and corresponds to the gauche2 structure in the table in Appendix 1 with the same energy to 5 decimal places. This suggests that the structure obtained from the previous calculation was close to a local minimum. This also suggests that the gauche2 conformer of 1,5-hexadiene is formed from the 'chair' transtion structure. We will now consider the other possible approaches to obtain a minimum geometry to see whether they confirm or disprove this suggestion.
Approach 2: Restart IRC & Increase Number of Iterations
This approach is said to be more reliable than Approach 1 but if too many points are used the wrong geometry can be obtained. The number of iterations was increased to 100 and the IRC was restarted. The results obtained are shown below.
File:DAAO IRC app2 calc summary.png


Even though it has been said that this approach is more reliable, we can see that after doubling the number of iterations the expected gauche2 structure has not been obtained. This structure has C2h symmetry and corresponds to the anti3 structure in the table in Appendix 1. From the graphs we can see that RMS gradient had not reached zero and so the minimum geometry was not achieved. This highlights a problem with this approach. Choosing the correct number of iterations can only be found through trial and error. Too few or too many iterations and the wrong geometry is obtained.
Approach 3: Redo IRC Computing Force Constants at Every Step
This approach is said to be the most reliable but it is not suitable for large systems and is expensive.


From the graphs above we can see that the RMS gradient reached zero and therefore the minimum geometry was obtained. As expected this approach yielded a structure which corresponds to gauche2. It can now be said we condfidence that the 'chair' transition structure leads to the gauche2 1,5-hexadiene conformer. Just like the gauche2 conformer, this structure has C2 symmetry and the energies agree to 5 decimal places.
Intrinsic Reaction Coordinate (IRC) Method for 'Boat' Transition State
The checkpoint file for the boat structure optimised using the QST2 method was opened. Using Gaussian, the job type IRC was chosen with the reaction coordinate computed only in the forward direction as it is symmetrical. The force constant was calculated once, IRCMax option was left unchecked and the number of points along the IRC was increased from the default 6 to 50.
After the job had finished, it was seen from the following that a minimum geometry was not reached.
File:DAAO Boat IRC 50 calc summary.png

File:DAAO Boat IRC 50 graphs.png
The RMS gradient did not reach zero. In order to achieve the geometry minimum 3 approaches discussed above were carried out for the 'boat' transition structure.
Approach 1: Run a Normal Minimisation on Structure Obtained After 50 Iterations

The structure achieved has C1 symmetry and corresponds to the gauche3 structure in the table in Appendix 1. Gauche3 is the lowest energy conformer in the table. This suggests that the 'boat' transition structure leads to the gauche3 conformer of 1,5-hexadiene.
Approach 2: Restart IRC & Increase Number of Iterations
Again, the number of iterations was increased to 100. The following results were obtained.
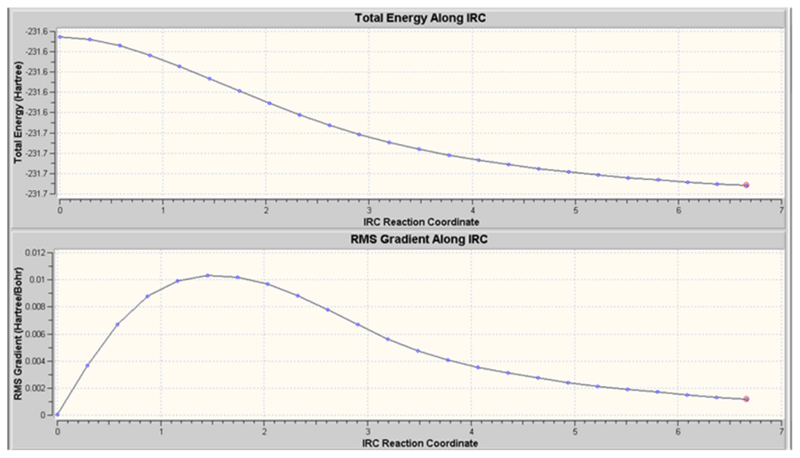
The struture obtained has CS symmetry and does not correspond to any of the structures in the table of Appendix 1. This is expected as the graph above shows that the RMS gradient had not reached zero and so the minimum on the PES had not been found. A higher number of iterations may have lead to the gauche3 structure and therefore would confirm that the boat transition struture leads to the gauche3 conformer as found above. This again highlights the issue of choosing the correct number of iterations.
Approach 3: Redo IRC Computing Force Constants at Every Step
In this approach, the IRC was redone computing the force constants at every step rather than once. It showed to be a reliable method above.


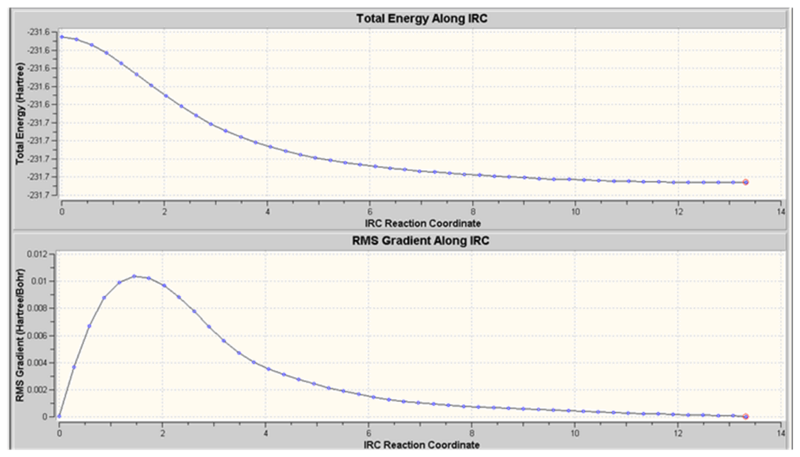
Just we saw for Approach 2, the structure obtained has CS symmetry and does not correspond to any of the structures given in Appendix 1. This is suprising as the IRC reaction coordinate vs RMS gradient showed that a minimum on the PES had been found. This suggests that maybe the wrong minimum was found. This result is disappointing as it now cannot be confirmed that the 'boat' transition structure leads to the gauche3 conformer.
Activation Energies for the Transition Structures
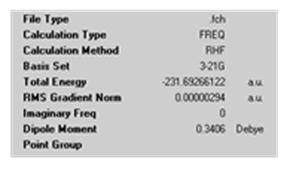
In order to calculate the activation energies for the reactions via both transition structures, one must first reoptimise both the 'chair' and 'boat' transtions strutures at the B3LYP/6-31G* level (and carry out frequency calculations). The appropriate section from the output files of the transition structures must then be compared to that of the anti2 structure. The results are shown below in a table where Ea (0K) is the activation energy at 0K. This is calculated as the difference between the sum of electronic and zero-point energies of the anti2 structure and each transition structure. Ea (298.15K) is the activation energy for the reaction at 298.15K. This is calculated as the difference between the sum of electronic and thermal energies of the anti2 structure and each transition structure.
| ’Chair’ | ’Boat’ | Anti2 | |
|---|---|---|---|
| Optimised Structure | File:DAAO chair reopt.jpg | File:DAAO boat reopt.jpg | 
|
| jmol | |||
| Calculation Summary | File:DAAO chair Ea calc summary.png | File:DAAO boat Ea calc summary.png | File:DAAO 1st anti reopt calc summary.png |
| Point Group | C2h | C2v | Ci |
| IR Spectrum | 
|

|
File:DAAO anti reopt IR.png |
| Imaginary Frequency/ cm-1 | -567 | -531 | n/a |
| Image of Imaginary Frequency | 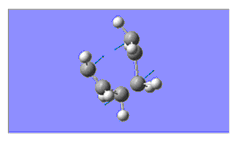
|
File:DAAO boat Ea vib.png | n/a |
| Excerpt of output file regarding Thermochemistry
|
File:DAAO chair Ea output.png | File:DAAO boat Ea output.png | File:DAAO 1st anti reopt thermo.png |
| Calculated Ea(0K)/ kcal/mol | Experimental Ea(0K)[2] / kcal/mol | Ea(0K) given in Appendix 1 [2] / kcal/mol | Difference between Calculated and Experimental Ea (0K)/ kcal/mol | Difference between Calculated and Appendix 1 Ea (0K)/ kcal/mol | |
|---|---|---|---|---|---|
| ’Chair’ TS | 34.04 | 33.5 ± 0.5 | 31.06 | 0.54 ± 0.5 | 2.98 |
| ’Boat’ TS | 41.94 | 44.7 ± 2.0 | 41.96 | 2.76 ± 2.0 | 0.02 |
| Calculated Ea(298.15K)/ kcal/mol | Ea(298.15K) given in Appendix 1 [2] / kcal/mol | Difference between Calculated and Appendix 1 Ea (298.15K)/ kcal/mol | |
|---|---|---|---|
| ’Chair’ TS | 33.15 | 33.17 | 0.02 |
| ’Boat’ TS | 41.31 | 41.32 | 0.01 |
We can see that the calculated activation energies agree well with the experimental and appendix values. The activation energy at both 0 and 298.15K is smaller for the ‘chair’ TS than the ‘boat’ TS. This means that under kinetic conditions the Cope rearrangement is more likely to proceed via the ‘chair’ TS leading to the gauche2 conformer of 1,5-hexadiene. Whereas under thermodynamic control the gauche3 conformer is more likely to form (as it is lower in energy) via the ‘boat’ transition structure.
As noted earlier there are only slight changes in the geometries of structures otptimised at different levels of theory (i.e. HF/3-21G and B3LYP/6-31G*).
Conclusion
This report has focussed on the Cope rearrangement. The reactants and products with an ‘anti’ or ‘gauche’ arrangement of the four central carbon atoms were optimised and discussed with regards to their strain and favourable interactions. It was found that gauche3 was the lowest energy conformer of 1,5-hexadiene despite its torsional strain and it was suggested that this was due to favourable interactions. Optimising at a low level of theory followed by a higher level has been demonstrated throughout the report. It was seen that very slight changes in the geometry have markedly different energies. Vibrational analysis was used to ensure that optimisation was successful considering that one would not expect any negative frequencies (imaginary frequencies) for reactants or products but only for transition states. For the ‘chair’ transition structure this frequency was at -818 cm-1 while for the boat it was at -840 cm-1. The transition structures were optimised through a variety of methods including the frozen coordinate and the QST2 methods. In order to ascertain which transition structure lead to which low energy conformer of 1,5-hexadiene, the IRC method was employed. The different approaches to achieve a minimum geometry from this method were also discussed. Suprisingly, it was found that Approach 1 was the most reliable and that the ‘chair’ and ‘boat’ transition structures lead to the gauche2 and gauche3 conformers of 1,5-hexadiene respectively. Finally, the activation energies of the Cope rearrangement via the ‘chair’ and ‘boat’ transition structures were calculated with good agreement with the values given in Appendix 1. It was seen that the ‘chair’ transition structure has a lower activation energy at both 0 and 298.15K and therefore it was suggested that the gauche2 conformer is the kinetic product of the Cope rearrangement while gauche3 is formed under thermodynamic conditions. Unfortunately due issues with the chemistry wiki during this computational module, the Diels Alder Cycloaddition section was not attempted.
References
- ↑ Wiest, O.; Black, K. A.; Houk, K. N., J. Am. Chem. Soc, 1994, 116 (22), 10336 DOI:10.1021/ja00101a078
- ↑ 2.0 2.1 2.2 [http://neon-tmp.cc.ic.ac.uk/wiki/index.php/Mod:phys3
Da907 01:09, 26 March 2010 (UTC)
