Rep:Mod:Crazy Guy Says "The End Is Niall"
Niall Killilea Computational Module 3
The Cope Rearrangement
The Cope Rearrangement is a concerted [3,3]-sigmatropic shift rearrangement of 1,5-hexadiene which can go through one one of two possible transition states, a chair shaped transition state and a boat shaped transition state (both of which are 6-membered rings):
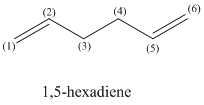

The aim of this exercise is to investigate the form and energies of the two transition states.
Optimizing Reactants And Products
The 1,5-hexadiene structure can exist in a wide variety of energetically stable conformers as the molecule contains 3 C-C single bonds, all of which are free to rotate. The 3,4 C-C bond can exist in one of two possible forms, the anti form and the gauche form, both of which are shown below in the sawhorse projection:

All listed conformers are named either anti or gauche- this is to explain the nature of the conformation around the 3,4 bond for the conformer. The structure of 10 possible conformations were examined. The structures were minimised using Hartree-Fock method with 3-21(G) basis set and then using DFT B3LYP method with 6-31(G). Listd below are the 10 conformers including the energies found:
| Confromer | Symmetry | Hartree-Fock Energy (hartree) | Difference in energy (hartree) | Structure |
| Anti 1 | C2 | -231.6926 | 0.0001 | |
| Anti 2 | Ci | -231.6925 | 0.0002 | |
| Anti 3 | C2h | -231.6891 | 0.0036 | |
| Anti 4 | C1 | -231.691 | 0.0017 | |
| Gauche 1 | C2 | -231.6878 | 0.0049 | |
| Gauche 2 | C2 | -231.6917 | 0.001 | |
| Gauche 3 | C1 | -231.6927 | 0 | |
| Gauche 4 | C2 | -231.6915 | 0.0012 | |
| Gauche 5 | C1 | -231.6896 | 0.0031 | |
| Gauche 6 | C1 | -231.6892 | 0.0035 |
The difference in energy is as compared to the energy of the lowest energy conformer, gauche 3. This is an unexpected result, as an anti structure was expected to be the lowest energy conformer- to explain this result the molecular orbital diagram must be analysed:

The HOMO shows strong overlap of the bonding π systems of the two alkene bonds, stabilising the conformer.
Thermodynamic Data
The energy data above cannot be compared to experimentally measured quantities, as they only represent single molecules. To ascertain the thermodynamic data, the 10 conformers were optimised using the B3LYP method and 6-31G basis set and then frequency measurements were carried out on the optimised structures. Opening the output log file of the frequency calculations, the following thermodynamic data can be found:

Listed below is the sum of electronic and thermal energies for the 10 conformers at 298.15K and at 0K:-
| Conformer | E(B3LYP) (hartrees) | Sum of electronic and thermal free energies at 298.15K (hatrees) |
| Anti 1 | -234.6096 | -234.5002 |
| Anti 2 | -234.6096 | -234.5008 |
| Anti 3 | -234.6075 | -234.4973 |
| Anti 4 | -234.6086 | -234.4995 |
| Gauche 1 | -234.6058 | -234.4955 |
| Gauche 2 | -234.6085 | -234.4993 |
| Gauche 3 | -234.6091 | -234.5001 |
| Gauche 4 | -234.6082 | -234.4987 |
| Gauche 5 | -234.6069 | -234.4974 |
| Gauche 6 | -234.6067 | -234.4974 |
As shown, at 298.15K, the most stable structure is the Anti 2 conformer, as the steric strain of the molecule dominates the choice of conformation. At 0K, on the other hand, Gauche 3 is the most stable conformation due to the additional stabilisation of the C=C π orbitals as described previously.
Transition State Structures And Energies
Chair Transition State
The chair transition state was characterised by optimising the structures to a TS(Berny) form.
Initial Optimisation
An allyl fragment, CH2-CH-CH2 was drawn out and optimised using the Hartree-Fock method and 3-21G basis set:
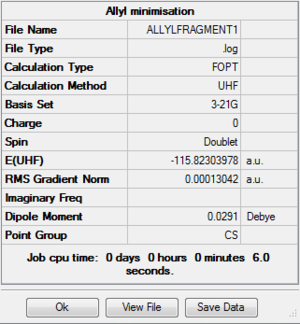
This allyl fragment was used in the approximation of the transition state before optimisation.
First Attempt At Optimisation
A "guess" structure of the transition state was set up by placing 2 of the previously optimised allyl fragments together in a C2h form as follows:
This structure was optimised using the Hartree-Fock method with a 3-21G basis set to a TS(berny). In the additional keywords was added the term Opt=NoEigen. The optimisation resulted in the following structure: A vibrational analysis of the transition state was also carried out in conjunction with the optimisation, and the vibrations included a molecular movement which corresponds to the change of the molecule during the breaking and formation of bonds during the Cope Rearrangement. The summary of the calculation and molecular vibration resulting in the imaginary frequency are as follows:

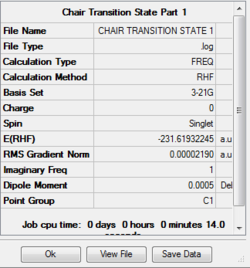
The inter atomic distance between the terminal carbons on each of the allyl fragments is 2.020Å.
Second Attempt At Optimisation
In order to gain a better picture of the transition stage, the optmisation was repeated using 2 separate stages, again using the Hartree-Fock method and 3-21G basis set:-
1. The same guess transition state from the first attempt was used. The inter atomic distance between the terminal carbons was fixed at 2.2Å using the Redundant Coordinate Editor.
2. The resultant structure was then modified on the Redundant Coordinate Editor, changing from "frozen coordinates" to "derivative". The optimisation was then repeated in conjunction with a frequency measurement, resulting in the following structure:. The summary of the optimisation is as follows:

Comparison Of Optimisations
Below are the comparisons of the two optimisations:
| Structure | First Optimisation | Second Optimisation |
| Energy (Hatree) | -231.61932 | -231.61932 |
| C-C bond length (inter-fragment) (Å) | 2.020 | 2.020 |
| C-C bond length (intra-fragment) (Å) | 1.389 | 1.389 |
The comparison shows no real difference between the two optimisations.
6-31G(d) Optimisation
Using the second resultant optimisation, the transition state was re-optimised to a TS(Berny) using the B3LYP method and 6-31G(d) basis set. This resulted in the following structure:. The summary of the optimisation is as follows:
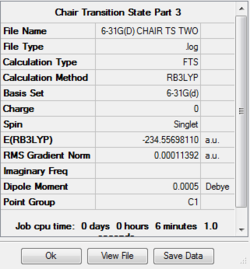
The bond length between the terminal carbons is 1.967Å which is in close agreement with the literature value of 1.971Å [1], and C-C bond length within the fragments is 1.408Å.
Comparison of the second optimisation to the 6-31G(d) optimisation is as follows:
| Structure | 6-31G(d) Opimisation | Second Optimisation |
| C-C bond length (inter-fragment) (Å) | 1.967 | 2.020 |
| C-C bond length (intra-fragment) (Å) | 1.408 | 1.389 |
The comparison shows that the B3LYP 6-31G(d) optimisation predicts that the fragments are closer together. The energies, however cannot be compared to each other, as they are calculated using different methods.
IRC Calculations
IRC stands for Intrinsic Reaction Coordinate- upon visualisation of the transition state, it is not possible to determine what the resultant form will be. The IRC is used to follow the reaction along the minimum energy path to the final optimised structure. IRC calculations of the optimised structure over 50 steps while only calculating the force constant once resulted in the following optimisation:


The final structure is as follows:
This is obviously not a completely optimised structure. In order to gain a final structure, there are three options:
Optimise The Final Output
The above final geometry was optimised using the B3LYP method and 6-31G(d) basis set, resulting in the following structure:. The summary of the optimisation is as follows:-
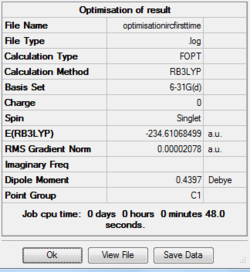
Increase The Number Of Points
In the initial IRC computation, the energy was optimised over 50 steps. Increasing the number of steps to 100 will increase the chance of finding a minimum energy conformer, resulting in the following final structure:jmol><jmolAppletButton><uploadedFileContents>Niallfinalchairtsircsecondtime.mol</uploadedFileContents><text>Click here for Jmol</text></jmolAppletButton></jmol>. The course of reaction is as follows:

Calculate The Force Constant
In the inital IRC, the force constant was only calculated once- calculating it more often will result in a structure more similar to the "real" final product. The IRC was therefore repeated, with 100 steps and calculating the force constant at each stage. The course of the reaction is as follows:

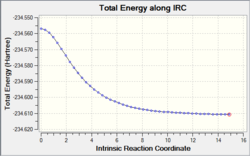
The overall final structure is:
Summary Of Chair Transition State
All of the IRC calculations point to the same final product: gauche 2. This is because the gauche form allows for better overlap of the π orbitals which is required to begin the overall reaction. The energy of the transition state was measured using B3LYP method and 6-31G(d) and found to be -234.557hartrees. The energy of the Gauche 2 reactant/product is known to be -234.4993hartrees- a difference of 0.0577hartrees (36.2kcalmol-1). This difference in energy is the activation energy for the chair transition state, and is in good agreement with the literature value of 33.5±0.5kcalmol-1[1].
Boat Transition State
The boat transition state was characterised and its energy calculated to a TS(QTS2) and later to a TS(QTS3). TS(QTS2) optimisation works by taking two inputs: a reactant molecule and a product molecule, and then calculating an energy maximum along the interchange of the two. TS(QTS3) uses 3 inputs: a reactant molecule, product molecule and a "guessed" transition state input to determine the output transition state. It is usually more accurate than the TS(QST2).
First Attempt
As a first attempt, two molecules of the anti2 were drawn onto Gaussview on the same input file, but separate windows. The numbering of the atoms on the molecules were changed, so as to look like this:
The calculation was then run, optimising the structures to "TS(QTS2)" using the Hartree-Fock method and 3-21G basis set. The calculation immediately failed, resulting in the following structure:. The reason that the optimisation failed is that the program is unable to manipulate the movement of the bonds- they appear to crash into each other during the process.
Second Attempt
To overcome this problem, the conformation of the 2 input files were modified so as to appear more similar to the boat transition state:-

The calculation was repeated, optimising to "TS(QTS2)" using the Hartree-Fock method and 3-21G basis set, resulting in the following transition state: . A frequency measurement was carried out on the resultant structure, and it was found that there is an imaginary stretching frequency corresponding to the bond formation and breaking during the Cope Rearrangement reaction at 839cm-1. The summary of the calculation and imaginary frequency movement are as follows:

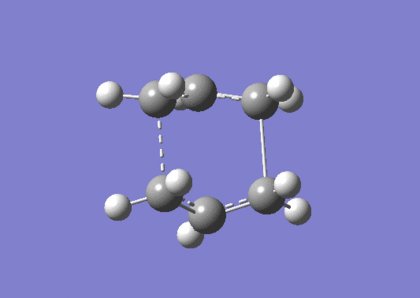
QTS3 Optimisation
The calculation of the transition state was repeated, optimising to a TS(QTS3) using the Hartree-Fock method and 3-21G basis set. The three input molecules are as follows:


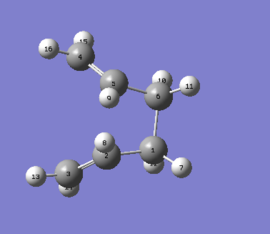
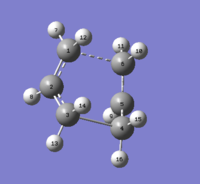
Optimisation resulted in the following structure:. The imaginary frequency occurred this time at -840cm-1. The summary of the optimisation and imaginary frequency are as follows:


Comparison Of QTS3 and QTS2
Below is a table listing data obtained concerning the TS(QTS2) and TS(QST3) optimisations:
| Structure | TS(QTS2) | TS(QTS3) |
| Energy(hartrees) | -231.6028 | -231.6028 |
| Bond length C1-C6 (Å) | 2.139 | 2.140 |
| Bond length C1-C2/C5-C6 (Å) | 1.381 | 1.382 |
| Bond length C2-C3/C4-C5 (Å) | 1.381 | 1.382 |
| Bond length C3-C4 (Å) | 2.140 | 2.140 |
The energies of the two transition states are identical, but the interesting difference is the C3-C4 and C1-C6 bond lengths:- these are the two bonds which are either breaking or forming during the course of the reaction and, because the reaction is symmetrical (reactants and products are identical), they are therefore expected to be identical. However, the QTS2 calculation predicts that C3-C4 is very slightly longer, perhaps due to inaccuracy in the calculation. The QTS3 predicts that they are the same, as predicted.
6-31G(d) Optimisation
The optimisation and frequency calculation of TS(QTS3) was repeated, using the DFT B3LYP method and 6-31G(d) method instead, resulting in the following structure:. The imaginary vibration in this case is found to appear at 530cm-1. The summary of the optimisation and imaginary vibration are as follows:
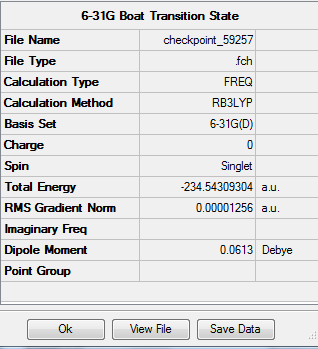
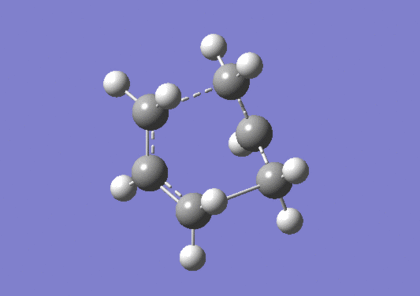
The overall energy is 234.543hartrees.
IRC Of Boat Transition State
The IRC of the boat structure was calculated using the same B3LYP method and 6-31G(d) basis set. The IRC proceeded as follows:
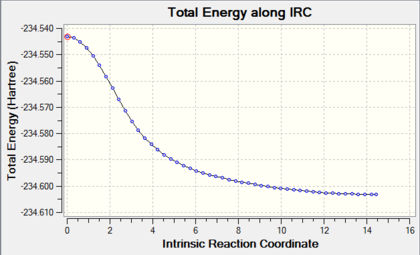
Optimisation of the final structure in the IRC resulted in the following structure:. The eclipsed geometry of the final structure is as expected, as it has the similar symmetry as the boat transition state.
Summary Of the Boat Transition State
The energy of the transition state was measured using B3LYP method and 6-31G(d) and found to be -234.4311hartrees. The energy of the Gauche 2 reactant/product is known to be -234.4993hartrees- a difference of 0.0682hartrees (42.8kcalmol-1).
Summary of Cope Rearrnagement Transition States
Diels Alder Cycloaddition
The Diels Alder Cylcoaddition is a concertd [4+2]-cycloaddition of an alkene to a diene, for example in the case of the addition of maliec anhydride to cyclohexadiene:-
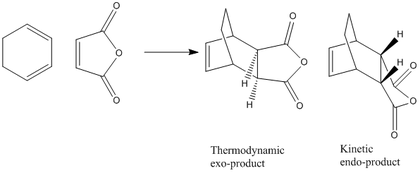
At room temprature and pressure, the reaction is under kinetic control; the kinetic endo-product dominates as there is not enough energy to overcome the energy barrier to form the thermodynamically more stable exo-product. The aim of this exercise is to investigate the transition state of the addition.
Addition of Ethene to Cis-Butadiene
The first cycloaddition is the addition of ethene to cis-butadiene to form cyclohexene:
Optimisation Of Reactants
Cis-butadiene and ethene were both optimised using B3LYP method and 6-31G(d) basis set:

Vibrational analysis of the cis-butadiene resulted in the following thermodynamic data:

The analysis shows that the sum of the electronic and thermal energies for the cis-butadiene is -155.927hartrees.
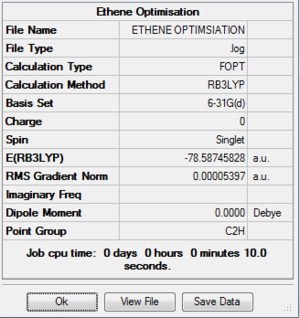
Vibrational analysis of the ethene resulted in the following thermodynamic data:
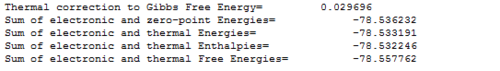
The analysis shows that the sum of the electronic and thermal free energies for ethene is -78.558hartrees. The sum of the electronic and thermal free enrgies for the two reactants is therefore -234.485hartrees.
Molecular Orbital Analysis of Reactants
The HOMO of the cis-butadiene is as follows:
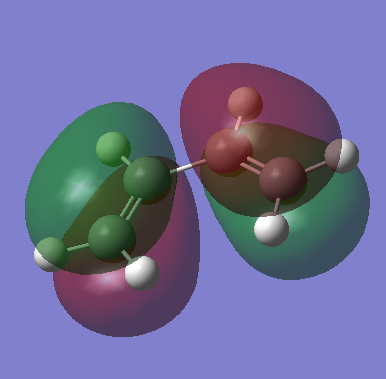
The molecular orbital is antisymmtric with respect to the plane of symmetry through the centre of the molecule. The LUMO of the ethene is as follows:

The molecular orbital is antisymmtric with respect to the plane of symmetry through the centre of the molecule.
Initial Optimisation of Transition State
A guess transition state was formed by drawing a bicyclocyclo compound and removing the side C-C link:
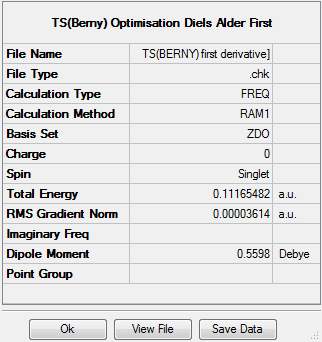
The transition state was then optimised using the semi-emperical AM1 to a TS(Berny), resulting in the following structure. The imaginary frequency corresponding to the bond formation during the Diels Alder cycloaddition occurs at -956cm-1. The summary of the transition state optimisation and the imaginary vibration is as follows:
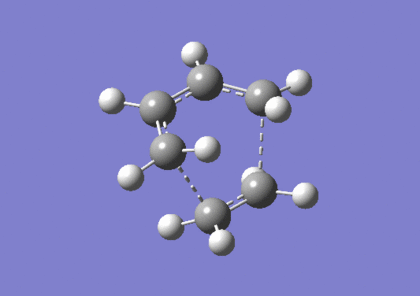
6-31G(d) Optimisation
Optimisation of the transition state using B3LYP method and 6-31G(d) basis set results in the following structure:. The imaginary frequency in this case occurs at 525cm-1. The summary of the optimisation is as follows:
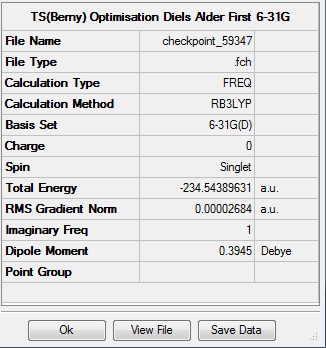
The thermodynamic data was read from the output file of the vibrational analysis:
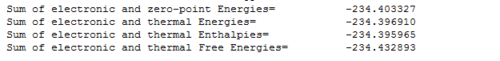
The sum of electronic and thermal free energies for the products is therefore -234.433hartrees. The energy of the reactants is -234.485hartrees, hence the activational energy for the reaction (difference between the reactant and transition state) at 298.15K is 0.052hartrees(32.6kcalmol-1).
Molecular Orbital Analysis Of Transition State
Shown below is the HOMO of the cycloaddition transition state:

It is evident that the molecular orbital is anti-symmetrical with respect to the plane of symmetry running trough the centre of the molecule, and is in fact a combination of the HOMO of cis butadiene and the LUMO of ethene- the overall reaction is therefore controlled by the overlap of these two orbitals.
It is for this reason that electron donating groups on the diene (to raise the energy of the HOMO) and electron withdrawing groups on the alkene (to bring down the energy of the LUMO) lowers the activational energy, increasing the rate of the reaction.
Addition of Maleic Anhydride To Cyclohexadiene
Optimisation Of Reactants
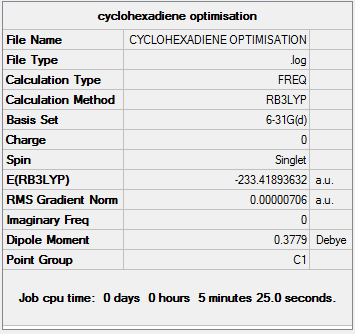
Cyclohexadiene and maleic anhydride were both optimised using the B3LYP method and 6-31G(d) basis set:

Vibrational anlaysis of the structure resulted in the following thermodynamic data:

As shown, the sum of the electronic and thermal free energies is -379.263hartrees.
Vibrational anlaysis of the structure resulted in the following thermodynamic data:

As shown, the sum of the electronic and thermal free energies is -233.324hartrees.
The sum of the electronic and thermal free energies for the two reactants is therefore -612.587hartrees.
Optimisation Of Exo-Transition State
The exo-transition state was optimised to a TS(Berny) using the B3LYP method and 6-31G(d) basis set, resulting in the structure below. The vibrational analysis shows an imaginary frquency at 449cm-1 corresponding to the bond formation during the course of the reaction:
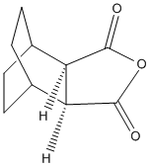
Vibrational anlaysis of the structure resulted in the following thermodynamic data:

The sum of the electronic and thermodynamic free energies for the exo transition state is therefore -612.534hartrees. It is already known that the sum of the reactant free energies is -612.587hartrees, hence the activational energy for the formation of the 0.053 hartrees (33.2kcalmol-1).
Optimisation Of Endo-Transition State
The endo-transition state was optimised to a TS(Berny) using the B3LYP method and 6-31G(d) basis set, resulting in the structure below. The vibrational analysis shows an imaginary frquency at 447cm-1 corresponding to the bond formation during the course of the reaction:
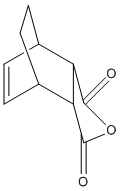
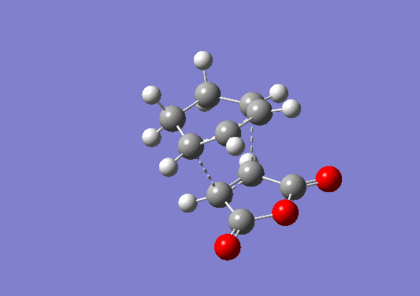
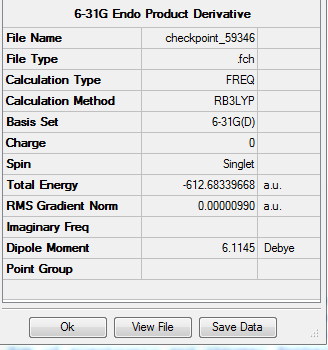
Vibrational anlaysis of the structure resulted in the following thermodynamic data:

The sum of the electronic and thermodynamic free energies for the exo transition state is therefore -612.538hartrees. It is already known that the sum of the reactant free energies is -612.587hartrees, hence the activational energy for the formation of the 0.049 hartrees (30.7kcalmol-1).
The endo-transition state is therefore more stable than the exo-transition state by an amount of 2.5kcalmol-1. This additional stabilisation can be explained by analysis of the HOMO of the endo transition state compared to that of the exo-transition state:
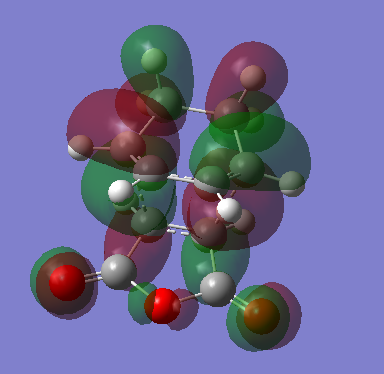
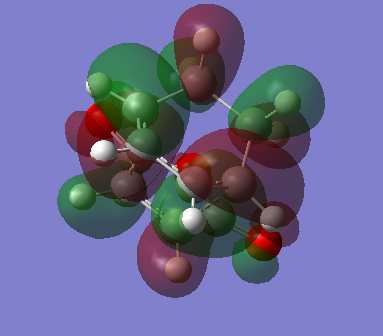
The endo-transition state shows that there is an additional orbital donation from the C=O orbitals, stabilising the overall structure.
References
- ↑ 1.0 1.1 Olaf Wiest et al., J. Am. Chem. Soc., 1994, 116 (22), pp 10336–10337; http://dx.doi.org/10.1021/ja00101a078
