Rep:Mod:CosGot

3rd Year Computational Chemistry Lab Report - Module 1
Student: Cosma Gottardi (Ceg08)

Section 1: Calculations using Molecular Mechanics

Hydrogenation of cyclopentadiene dimers

Cp dimers (1, 2) are different: endo, exo.

MM energy above shows that exo more thermo stable.

What makes endo less stable? compare the torsional energy - about 2 kcal per mol higher for endo than for exo conformer

however endo is formed

since 2 is the correct form, the process must be kinetic.

Why is it formed? Favourable orbital overlap in the transition state

Relative energetic contributions to different isomers in kcal/mol	Exo dimer (1) Exo Dimer (1)	Endo dimer (2) Endo Dimer (2)	Hydrogenation Product 3 Hydrogenation Product 3	Hydrogenation Product 4 Hydrogenation Product 4
Stretch	1.29	1.25	1.28	1.10
Bend	20.58	20.85	19.86	14.52
Stretch-Bend	-0.84	-0.84	-0.83	-0.55
Torsion	7.66	9.51	10.81	12.50
Non-1,4 Van der Waals forces	-1.42	-1.54	-1.22	-1.07
1,4 Van der Waals forces	4.23	4.32	5.63	4.51
Dipole-dipole interactions	0.38	0.45	0.16	0.14
Total Energy	31.88	34.00	35.69	31.15

Note: molecules 1, 2 and 4 all have enantiomers which have identical energies and are not shown. Molecule 3 has two different conformations of the five-membered ring of which the one with lower energy is shown. The energy of the other conformer is 35.93 kcal/mol, or about 0.5 kcal higher. The difference in shape is that the highlighted atom points more inward towards the double bond.

Hydrogenation.

Which one is formed - 3 or 4?

4 is thermo more stable, so would form under equilibrating conditions, 3 might be formed if reaction kinetics would favour it.

Literature says 4 is formed under equilibrating conditions (1.5h, 60-70 °C).

We cannot say which is the kinetic product, but 4 definately wins here.

Backwards and forwards reactions = equilibrating = the thermo product wins.

Preferred face of attack in the nucleophilic addition to a pyridinium ring - stereochemical aspects

Molecule 5

Nucleophilic attack of methyl magnesium iodide on 5 to give 6. Image taken from mod:organic

We are considering the reaction shown in the picture on the right (click it to enlarge), and trying to determine why the methylation occurs predominantly on the "top" face.

Using the MM2 Molecular Mechanics geometry optimisation technique implemented in Chemdraw, several conformers were found - they can be distinguished by the puckering of the 5-membered ring and whether the ether-oxygen in the 7-membered ring (atom number 9 in the animation) is up or down with respect to the carbon atom (No. 10). The energetically most stable conformation can be seen in this animation:

The table below summarises the conformers found and their respective energies. Also, the dihedral highlighted in the animation is reported - it serves as a measure of how far "above" the plane of the 6-membered ring the carbonyl oxygen lies.

Note: above, up, down, etc. when referring to the position of atoms in the molecule are relative to the orientation of the molecule as shown in the reaction diagram and the jmol applet.

Selected conformers of molecule 5	Energy in kcal/mol relative to lowest energy conformer	puckering of 5-membered ring	conformation of 7-membered ring	Dihedral angle
Conf 1	0.00	atom 4 down	oxygen down	10.4°
Conf 2	0.95	atom 4 up	oxygen up	23.6°
Conf 3	1.27	atom 4 down	oxygen up	23.4°
Conf 4	1.45	atom 4 up	oxygen down	12.6°

Several other modelling techniques (MMFF94, MOPAC/PM6) were used and dihedral angles ranging between 8° and 38° were found, however (through manual re-positioning of atoms and re-optimising of the geometry) no (stable) conformation could be found in which the carbonyl Oxygen was below the aromatic ring. This, further to the fact that the stablest MM2-conformer has a dihedral angle of about 10°, makes it clear that the carbonyl oxygen will barely ever be found below the plane but rather above. Turning to the reaction, we now consider the approaching Grignard Reagent. It is postulated that the Magnesium atom coordinates to the carbonyl oxygen, and both being above the molecule, steer the Methyl onto the top face of the aromatic ring, resulting in molecule 6 (after work-up) in high yield (generally >85%) and selectivity (19:1).

A more precise way of modelling the angle could have been achieved by modelling the stage of the reaction where the Mg has coordinated to the carbonyl oxygen. Using the molecular mechanics approach this is however not possible, since it does not generally support metals.

Molecule 7

Nucleophilic attack of aniline on 7 to give 8. Image taken from mod:organic

Just as above, the conformation that the reactant (here molecule 7) is in, affects the side that the incoming nucleophile (here aniline, (C₆H₆)NH₂) attacks on. It has been reported in this reaction that the aniline prefers to attack on the face opposing the side carbonyl group's oxygen is on - i.e. if it was lying above the ring which is to be attacked, the aniline would add to the bottom side, leaving the H that was already on the attacked carbon on top.

So, just as for molecule 5 above, different conformations were searched for by optimising different starting geometries using MM2. Conformational elements that resulted in significant conformations were:

1. whether when the "methyl group N" (attached to the positively charged nitrogen atom) is above or below the plane of the single six-membered aromatic ring,
2. whether the other methyl group (labelled "methyl group C" in the Jmol animation) lies above or below the isopropyl group.

A 3D model shows best where these are located: (lowest energy conformation with several groups labelled) With these two points playing into our conformational analysis, we get 2²=4 permutations and hence 4 conformers:

Conformations of molecule 7	Energy in kcal/mol	Dihedral angle	isopropyl group	methyl group N
Conf 1	83.8	28.8°	above methyl group C	above single aromatic ring
Conf 2	66.25	19.9°	above methyl group C	below single aromatic ring
Conf 3	63.36	-20.0°	below methyl group C	above single aromatic ring
Conf 4	80.26	-20.1°	below methyl group C	below single aromatic ring

Notes:

• All energies are energies that have been outputted by the MM2 calculation. They are not thermodynamic quantities and should only be compared to each other.
• "above", "below", etc. refer to the position of the molecule with respect to the plane of the double aromatic ring - with "above" being the upper face in both the diagram and the jmol.
• The dihedral angles quoted are measured as described for molecule 5. Negative numbers mean that the O atom is below the plane of the double aromatic rings.

As we can see from the table above, the conformation with the energy of 63.36 is the most stable - and hence the attacking nucelophile is most likely to find 7 in this state. The carbonyl-oxygen atom being below the plane of the double aromatic ring that is being attacked will now result in an attack on the top face as discussed above, hence giving molecule 8.

On further investigation of 7, one could find the transition states between the conformations to show how high the energy barrier is for the carbonyl O to "switch side".

the conformation/atropisomerism of a large ring ketone intermediate in one synthesis of the anti-cancer drug Taxol

The molecule considered in this part is an important intermediate, as reported by Paquette, in the synthesis of taxol, an anticancer drug whose total synthesis was one of the first syntheses of a rather complex organic molecule to be archived, showing the power of organic synthetic strategy and the systematic use of protecting groups.

Again, our interest lies in the different conformations that this intermediate can assume: one with the oxygen of the carbonyl group pointing "up" or down (with respect to the Jmol applets and drawings below). Using Chemdraw and the MM2 force field optimisation, several conformations were found, both with the oxygen pointing up and down. Apart from this, the difference between them was mainly in the conformation of the six-membered cyclohexane ring. Through manual alterations i.e. adjusting the positions of the atoms and re-minimising the energy, the stablest conformers for both the oxygen pointing up and down were found to be when the cyclohexane ring was in a chair conformation. These conformations (minimised by MMFF94) are reported in the table below.

Atropisomers of a precursor of Taxol	Atropisomer 9	Atropisomer 10
Conf 1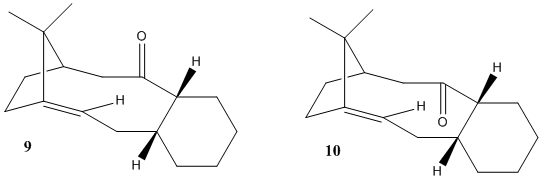
Jmol applets	O up	O up
MM2 Energies	48.87 kcal/mol	44.27 kcal/mol
MMFF94 Energies	70.53 kcal/mol	60.54 kcal/mol

The difference between a previously MM2 optimised conformation after re-optimisation with MMFF94 was minimal. This is probably due to the fact that the "best" conformation had already been found with MM2.

As one can see from the table, 10 is the atropisomer with energy significantly lower than 9, and this result is confirmed by both MM2 and MMFF94 force fields. Given the fact that only one of the two is synthesised in the preceding step of the taxol synthesis and the other one forms from the former spontaneously while standing on the bench^Mod:organic, we can safely say that it is 9 that is formed initially and turns into 10, being the more stable of the two. This difficult interconversion is an example of atropisomerism.

Another interesting point about this molecule is the fairly small reactivity that it has at the double bond compared to other alkenes.^Mod:organic This can be explained through hyperstability - the phenomenon that due to other conformational restrictions on a carbon-carbon bond (here arising from the bridge that separates the 10-membered ring from the 5 membered ring), a double bond, giving the carbon atoms involved sp² geometry, is favoured over single bond, which would necessitate the carbons being sp³ and subject the molecule to more strain.

Hence, if one wanted to hydrogenate the double bond to the parent carbon-carbon single bond one would have to overcome this strain, which explains the extra stability.

Having used primarily empirical methods, MM2 and MMFF94, which find best bond lenghts and angles by solving simple quadratic equations that have only empirical parameters, to solve the problems in Section 1, we shall now employ a technique that also takes into account electronic contributions and hence can calculate a few more useful properties, such as molecular orbitals, charge densities and some thermodynamic properties.

Regioselective electrophilic addition to a bicyclic, bridged di-alkene

An electrophile, such as dichlorocarbene, will usually readily attack a C=C double bond, because it is very electron rich compared to C-C single bonds. However in the present Molecule 12, one of the two enes is attacked much more easily than the other. Visualisation of the molecular orbitals that are usually significant in reactions (the highest one occupied by electrons (HOMO) and the ones below (HOMO-1, etc.) and above (LUMO, LUMO+1, etc.) it) provides good insight into this problem.

MO orbitals for this lab had to be hosted on my personal site. Click here to view

Looking at the HOMO above, we can see that a lot of the electron density is around the double bond that is endo to the chlorine atom. This is a first indication that this double bond is very electron rich and hence prone to attack. However looking at the HOMO-1 we see that there is also a lot of electron density on the exo carbon-carbon double bond orbital. The reason why the HOMO-1 is below the HOMO is becasue of its antiperiplanar overlap with the C-Cl σ* orbital, "rendering the endo double bond more nucleophilic in both a frontier orbital and an electrostatic sense."

Vibrations

...

Mini-Project: Stereoselective dissolving metal reductions

The reaction studied here is a selective Birch reduction of a Ketone 5 to an Alcohol 6, where the isomer 6a is formed, not 6b.

Scheme of the reaction with numbering system used in the primary reference and this report.

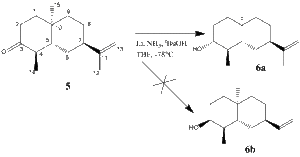
• How would you tell the reaction had worked, and which stereoisomer had formed?

To see if the reaction has worked, one can record an IR spectrum of the starting material and the final material and see if the carbonyl peak for the Ketone 5 (expected around 1700 cm^-1) has disappeared in the IR spectrum of 6 and replaced by a broad O-H peak somewhere above 3000.

To determine which stereoisomer of the alcohol, 6a or 6b, has formed is a bit trickier. My suggestion would be to look at the vicinal (³J) coupling constants of the proton attached to the ³C. Since the 1-2-3-4-5-10 ring is locked into a chair position by virtue of the methyl group 15, the OH will be equatorial in 6a leaving our proton of interest in the axial position (equatorial for 6b). In 6a, it is now anti-periplanar (app) to two protons (on 2C and 4C) and gauche (synperiplanar) to one (on 2C). In contrast, isomer 6b, it would be in a gauche relationship to all of those three protons.

Karplus plot

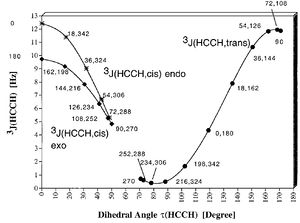
With knowledge of the Karplus equation (a graphical representation of which is given) we can estimate that for compound 6a we would expect one ³J = ca. 12 Hz and the other two ³J to be about 4 Hz, i.e. it would be ddd which could look more like a dt if the two gauche proton coupling constants are very similar. For 6b we can expect a ddd which could turn into a q if the coupling constants are similar, but the first and the last line shouldn't be more apart than about 12 Hz in total (as opposed to 6a, where one of the coupling constants is already 12 on its own).

All of this deduction was without taking into account that we might also see some coupling from the -OH proton, which would again split the signal into two, making it a fairly complex multiplet, but since the -OH proton and our proton on the 3C carbon both have fairly unique and distinct shifts in the spectrum of the molecule, one should be able to work back, given a high resolution NMR spectrum.

• Do the predicted 13C (and 3JH-H) data match the reported?

Below is a table with the 13C NMR Data found in the literature for 6a and how it compares to that calculated using Gaussian (using the mpw1pw91 DFT with the 6-31(d,p) basis set):

Carbon #	δ literature	δ calculated	difference between δ lit and δ calc
1	39.93	41.42	1.49
2	30.92	30.57	-0.35
3	76.86	74.21	-2.65
4	38.88	42.38	3.50
5	43.22	41.26	-1.96
6	26.05	33.00	6.95
7	39.19	37.85	-1.34
8	23.08	25.65	2.57
9	37.1	39.00	1.90
10	33.78	33.68	-0.10
11	147.11	149.39	2.28
12	22.82	24.04	1.22
13	110.67	104.94	-5.73
14	14.87	15.47	0.60
15	16.68	24.12	7.44

The overall match is pretty good, however based on the calculation (and respecting the proton coupling multiplicities from the original spectrum) I would re-assign the 38.88 ppm resonance from the paper to the 5C carbon (not 4C) and the 43.22 resonance instead to 4C, giving a better match. Also the calculation for the 6C carbon is not ideal compared to the experimental data.

• Why was this stereoisomer obtained?

Top face of 5 is less hindered and more prone to attack, the bottom face has much steric hinderance (through Methyl group 15) for the incoming tBuOH to provide a hydrogen. The cold conditions make this process kinetically favourable resulting in 6a, although 6b is thermodynamically slightly more stable, as has been found by calculation of the Heat of Formation using the MOPAC PM6 method:

  MOPAC 6a: -84.56 kcal/mol
  MOPAC 6b: -85.22 kcal/mol