Rep:Mod:Computationalreport1C

Synthesis and Computational Lab: 1C

Part 1: Introduction to Molecular Mechanics

Introduction to MMFF94 and MMFF94s

With the improvement of computational data and computer processing power, the usage of molecular mechanics/dynamics forcefield has become very integrated in predicting properties of chemical molecules. A molecular mechanics/dynamics forcefield should be able to predict characteristics such as molecular geometries, conformational/stereoisomeric energies, vibrational frequencies etc. to a reasonable accuracy as compared to experimental-derived values.

Building on work from Kollman et al. s’ AMBER forcefield and Allinger et al. s’ MM1, MM2, MM3 and MM4, Merck Research Laboratories have managed to optimized and improved the previous computational algorithms and produced MMFF94 (Merck Molecular Force Field 94). One of the most prominent advantages of MMFF94 over other preceeding work is its enhanced prediction accuracy. The reason lies in the fact that MMFF94’s core parameterization utilizes an unprecedently large amount of computational data obtained from ab initio calculations¹.

Subsequently after the development of MMFF94, a new “static” variant of the MMFF was introduced i.e. the MMFF94s. Unlike MMFF94 that was developed for the use of molecular dynamics simulations (which can be expensive), MMFF94s was developed with the purpose of energy minimization studies in mind. Although both systems provide identical results for most systems, they differ for amides and unsaturated amines which contain resonance-delocalized trigonal nitrogen atoms².

In this computational exercise, MMFF94s is used predominantly as oppose to the alternative Universal Force Field (UFF). Although versatile across the entire periodic table, UFF is derived from simple rules and atomic parameters such as fixed hybridization that increases the likelihood of erroneous structural and energetic predictions³.

Forms of MMFF94s

Steric energy of a molecule is the energy arise due to its geometry or conformation. Energy minimization of steric energy process ensures that the molecule is in its lowest energy conformation.

MMFF94s assumes that the total steric energy of a molecule can be found by the sum of a few specific interactions in a molecule.

                                                ES = EBS + EAB + E SB + ET + EOOP + EVdW + EEE

where the bonded interactions are:

E_S = Total Steric energy

E_BS = Total Bond Stretching energy

E_AB = Total Angle Bending energy

E_SB = Total Stretch Bending energy

E_T = Total Torsional Energy

E_OOP = Total Out-Of-Plane Bending energy, and

where the non-bonded interactions are:

E_VdW = Total Van der Waals Energy

E_EE = Total Electrostatic Energy

Types of Energies	Explanation
Bonded Interactions
Total Bond Stretching Energy	The total bond stretching energy is related to the vibration energy of the molecules in comparison to the equilibrium bond length. Whenever a bond deviates from the equilibrium bond length, the energy value increases. MMFF94s uses a quartic function that has the force constant term (relate to bond strength). The quartic function term is superior to the cubic function term (used in MM2) in the sense that it avoid the “cubic stretch catastrophe” where progressive elongation of molecule bond length leads to negative infinity.
Total Angle Bending Energy	Similar to Total Bond Stretching Energy, the total angle bending energy is also related to the vibration energy of the molecules about the equilibrium bond length. However, unlike EBS that measures the bond strength, EAB is associated with the stiffness of the molecules based on the Hookiean potential. Whenever bond angles deviate from the norm during vibration, this energy term increases as well.
Total Stretch-Bending Energy	This energy term takes into account of the energy due to increase in bond length when bond angle between two atoms changes.
Total Torsional Energy	Total torsional energy is the energy required for intermolecular rotation about the bonds. In molecule mechanics, however, this term is often used as a correction that must be added or subtracted to the total energy of the molecule to fit a quantum mechanical calculation about the dihedral angles of bonds.
Total Out-Of-Plane Bending Energy	This energy term refers to the energy needed to deform the dihedral angle (zero degrees) of a planar group of atoms such as carbonyl or amide functional groups.
Non-Bonded Interactions
Total Van der Waals Energy	The total Van der Waals energy term examines the intramolecular interactions such as repulsion or attraction between non-bonded atoms in the molecule. This term is crucial in determining the preferred conformation of the molecule. MMFF94s employs the novel “Buffered-14-7”. The name is derived from a buffering constant and the 14th and 7th power dependencies of the repulsive and attractive energy in the equation.
Total Electrostatic Energy	The total electrostatic energy functions take into account of the Coulombic potential and partial charge/dipole/atomic point charges interactions within the molecule.

Part 2 : Conformational Analysis Using Molecular Mechanics

The Hydrogenation of Cyclopentadiene Dimer

Endo and exo adduct from the Dimerization of Cyclopentadiene

Cyclopentadiene will undergo dimerization by Diels-alder reaction to form either an endo or exo adduct.

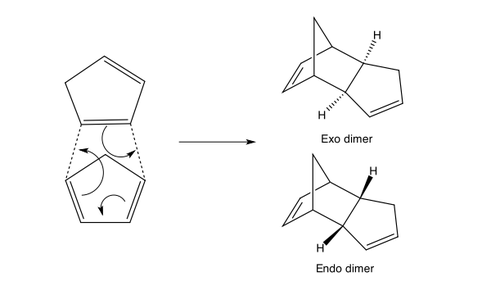
Stereoselectivity of Dimerization of Cyclopentadiene

Although the exo adduct is thermodynamically more stable than the endo adduct, the endo adduct is form preferentially. Using the QST2 method, the transition state of the Diels Alder dimerization was found. It was discovered that due to the secondary orbital interactions in the endo transition state, the endo dimer is formed preferentially (the kinetic product). Hence, it is proven that the Diels Alder dimerization between two cyclopentadiene are kinetically controlled.

Endo Transition State of Dimerization of Cyclopentadiene	Imaginary Stretch Frequency (-881.25) of the Endo Transition State (click to animate)	Secondary Orbital Interaction (Red overlapping orbitals)
Endodimer

Asynchronous Bond Formation of Dimerization of Cyclopentadiene

The initial study of the molecular orbitals of the transition states seemed a bit peculiar. Instead of getting a LUMO with symmetrical orbitals, the calculations showed a HOMO that is asymetric at the carbons where the new sigma bonds will be formed. Running an IRC further, it soon became clear that the asymmetry of the HOMO leads to an asychronous bond formation before leading to the product.

IRC plot following the Endo Transition State	IRC following the Endo Transition State (click to animate)	Asymmetry of orbitals at the carbons where the new sigma bonds will be formed

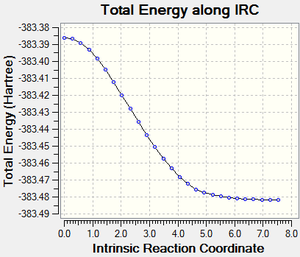Comparison of Energies between the Endo and Exo adduct of Dicyclopentadiene

Endo Adduct of Dicyclopentadiene dimerization	Exo Adduct of Dicyclopentadiene dimerization
Endodimer	Exodimer

Using MMFF94s ab initio calculations, the energies for the exo dimer and the endo dimer are derived.

	Energies
	ES	EBS	EAB	ESB	ET	EOOP	EVdW	EEE
Exodimer	55.374	3.543	30.772	-2.041	-2.728	0.015	12.800	13.014
Endodimer	58.191	3.468	33.187	-2.082	-2.950	0.023	12.360	14.186

The MMFF94s steric energy (after minimization) for the exo dimer is lower than that of the endo dimer. This is reflected by the large difference for the E_EE between the endo dimer and the exo dimer due to unfavourable steric repulsion between the two “arched down” cyclopentene rings.

Hydrogenation of Dicyclopentadiene

Hydrogenation of the endo dicyclopentadiene (DCPD) would lead to two potential products: dihydro product 1 and dihydro product 2.

Using MMFF94s, the energy of the two dihydro products are calculated.

	Energies
	ES	EBS	EAB	ESB	ET	EOOP	EVdW	EEE
Dihydro Product 1	50.123	3.308	30.864	-1.927	0.060	0.015(2)	13.281	5.121
Dihydro Product 2	41.257	2.823	24.685	-1.657	-0.379	0.000(2)	10.639	5.147
Tetrahydro Product	39.042	2.730	25.151	-1.676	1.287	0.000	11.551	0.000

From the MMFF94s calculation, it can be seen that dihydro product 2 has a lower steric energy than dihydro product 1. Therefore, dihydro product 2 is the thermodynamic product for the hydrogenation of dicylopentadiene. And indeed, this was what was observed by Skala et al.. He observed that the first hydrogenation occur at the norborene part of the molecule (rate of hydrogenation several times faster than that in the cyclopentene ring)6. The first heat of hydrogenation at the norborene is 138.8 kJ/mol while the second hydrogenation at the cyclopentene right is 109.5 kJ/mol⁶.

From the above results, it is also obvious that tetrahydro product is much more stable than either dihydro product. And yet, studies have shown that the tetrahydro product will only form after prolonged hydrogenation under high temperature. However, subjecting DCPD to high temperature leads to low yield due to cracking of DCPD.

Since thermodynamically it is predicted to form favourably, the fact that it does not could only mean that the hydrogenation of DCPD to tetrahydrodicyclopentadiene (TH-DCPD) is kinetically controlled. Most possibly, the transition state of the hydrogenation of DCPD is highly unstable hence it is unlikely to form.

Atropisomerism in an Intermediate related to the Synthesis of Taxol

Atropisomerism is a type of stereoisomerism that is form as a result of hindered rotation about a single bond.

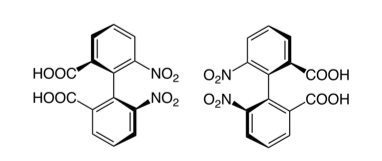
In the case of the 6,6’-dinitro-2,2’-diphenic acid, rotation about the bonds joining the two substituted phenyl rings would have to overcome large steric interaction between the bulky substituents. The barrier of rotation is high enough for the two conformers to be isolated individually.

In the synthesis of taxol, one of the key intermediates exhibit atropisomerism.

Atropisomerism in Taxol Synthesis

For the key intermediate, rotation about the carbon-carbon bonds would lead to two types of atropisomers, each with either the carbonyl group poining upwards or downwards in relative to the bridge.

Once again by using MMFF94s ab initio calculations, the steric energies for the two intermediates are illustrated as below:

	Energies
	ES	EBS	EAB	ESB	ET	EOOP	EVdW	EEE
Intermediate 9	70.571	7.743	28.356	-0.062	0.004	0.949	33.293	0.288
Intermediate 10	60.553	7.599	18.838	-0.139	0.199	0.844	33.269	-0.056

Analyzing the data above, the largest energy difference between Intermediate 9 and Intermediate 10 stems from the E_AB which is related to the strain of the ring. Intermediate 9 has an excess of 9.518 kcal/mol E_AB as compared to Intermediate 10. This comes as a surprise as intermediate 9 is predicted to be more stable alkene.

The rationale behind the prediction of the stability of intermediate 9 stems from the fact that the through-space distance of the upward-pointing carbonyl oxygen with the carbon-carbon is further than the through space distance between the downward-pointing carbonyl oxygen with the -CH₂-CH₂- fragment at the norbornene part in intermediate 10.

Hyperstable Olefins

Intermediate 9 and Intermediate 10 does not react readily with other reagents during functionalization. This is due to the hyperstability effect found in hyperstable olefins.

Hyperstable olefins are alkenes that contain less strain in the ring (i.e. negative olefin strain values) compared to the parent hydrocarbon. To study this further, further MMFF94s calculation was done to compare Intermediate 10 with the parent hydrocarbon.

The energies that we calculated are tabulated as shown below:

	Energies
	ES	EBS	EAB	ESB	ET	EOOP	EVdW	EEE
Intermediate 10	44.878	5.211	15.488	-0.267	-1.655	0.998	25.014	0.088
Parent Hydrocarbon	50.564	4.692	21.979	0.109	-0.958	0.247	24.495	0.000

Scrutinizing the results, the largest energy difference between intermediate 10 and the parent hydrocarbon stems from the Total Angle Bending Energy, EAB. Since the Total Angle bending energy is related to the angle strain in the molecules, it is apparent that the parent hydrocarbon has more ring strain as compared to the bridgehead olefin.

Part 3 : Spectroscopic Simulation Using Quantum Mechanics

Spectroscopy of an Intermediate Related to the Synthesis of Taxol

Molecule 17 and 18 are derivatives of intermediate 9 and 10. In this exercise, MMFF94s is used to predict the 1H and 13C NMR of molecule 17 and molecule 18.

NMR Spectra of Molecule 17

Endodimer

¹H NMR Spectra of Molecule 17

1H NMR Spectra of Molecule 17 Full Spectra	1H NMR Spectra of Molecule 17 Truncated Spectra

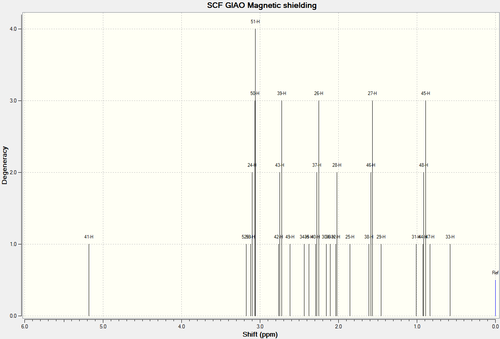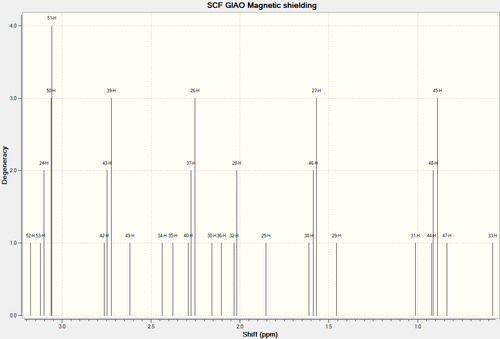H-Atoms	Chemical Shift (ppm)	Integration Height/Degeneracy	Literature values	Comments
41	5.1825	1	5.21	The first three results were fairly straight forward to be deduced and correlate wit experimental data. The hydrogen atom that is geminally attached to the carbon of the double bonds is the most deshielded due to the ring current anisotropic effect of the ring current The second most deshielded hydrogen atom is the hydrogen atom on the methyl group on the bridge. The hydrogen atom is pointing directly to the oxygen atom of the carbonyl functional group. The peaks with an integration height of 4 is assigned to the hydrogen atoms in the 1,3-dithiolane ring fragment. Subsequent analysis of the 1H NMR became very complicated very quickly for two reasons: 1. Gaussian calculations showed some atoms with an integration height of 3. Comparing their file atom number and checking their chemical environment, it is not possible to find any correlation between them. 2. Some of the peaks in the literature remains unresolved and are given as multiplets or grouped together.
52	3.1775	1	2.99
53,52,50,51	3.0867	4	3.40-3.10
42,43,39	2.7445	3
49	2.6187	1
34	2.4371	1
35	2.3782	1
40,37,26	2.2730	3
30	2.1566	1
36	2.1033	1
32,28	2.0259	2
25	1.8535	2
38,46,27	1.5898	3	1.25
29	1.4557	1
31	1.0123	1
44,48,45	0.9087	3	1.10
47	0.8354	1
33	0.5790	1

¹³C NMR Spectra of Molecule 17

13C NMR Spectra of Molecule 17 Full Spectra	13C NMR Spectra of Molecule 17 Truncated Spectra

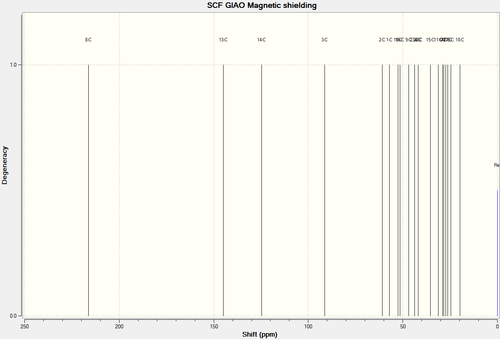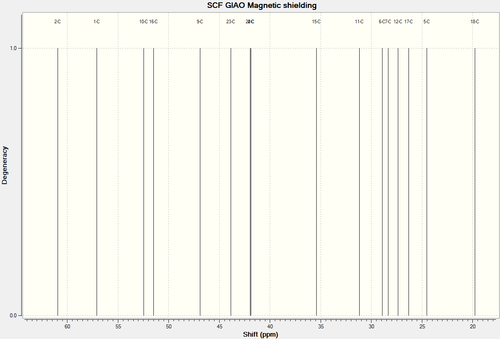C-Atoms	Chemical Shift (ppm)	Integration Height/Degeneracy	Literature Values	Image of carbon skeleton
8	216.2725	1	218.79
13	144.8626	1	144.63
14	124.7193	1	125.33
3	91.3340	1	72.88
2	60.9568	1	56.19
1	57.0811	1	52.52
10	52.4663	1	48.50
16	51.4857	1	46.80
9	46.9196	1	45.76
23	43.8647	1	39.80
22	41.9450	1	38.81	Comments
4	41.8724	1	35.85	The carbon bonded to the oxygen atom is the most deshielded, as is shown in the predicted values and the experimental values. There is a deviation between the values. Quite possibly, this is due to the fact that in reality, the carbonyl functional group is pointing slightly towards the equatorial position rather than a lateral position relative to the ring (as is in the input for Gaussian calculation) Most of the 1CNMR values that was predicted by Gaussian are all within an acceptable range of deviation. However, there is carbon 3 that has significant deviation between the predicted value and experimental value. Carbon 3 is the carbon bonded to the two sulphurs in the 1,3-dithiolane ring fragment. Such a huge deviation would possibly mean that the conformer that was given as input to Gaussian differs from the literature. The above NMR spectra was corrected with a level of theory B3LYP/6-31G(d,p) using TMS as reference and in chloroform.
15	35.4348	1	32.66
11	31.1964	1	28.79
6	28.9432	1	28.29
7	28.3640	1	26.88
12	27.3767	1	25.66
17	26.3311	1	23.86
15	24.5483	1	20.96
18	19.7788	1	18.71

NMR Spectra of Molecule 18

Endodimer

¹H NMR Spectra of Molecule 18

1H NMR Spectra of Molecule 17 Full Spectra	1H NMR Spectra of Molecule 17 Truncated Spectra

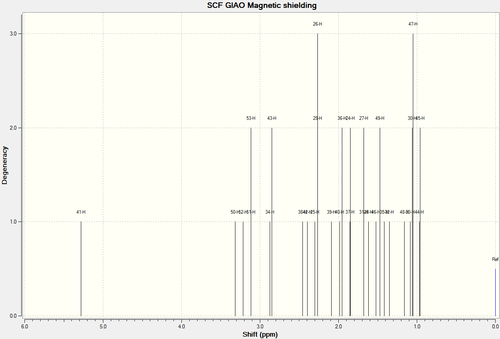H-Atoms	Chemical Shift (ppm)	Integration Height/Degeneracy	Literature values
41	5.2832	1	5.21
50	3.3175	1	3.00-2.70
52	3.2153	1
51,53	3.1161	2
34,43	2.8606	2
38	2.4549	1
42	2.3968	1
25,29,26	2.2796	3
39	2.0844	1
40,36	1.9699	2
37,24	1.8519	2
31,27	1.6780	2
28	1.6175	1
46,49	1.4979	2
35	1.4150	1
32	1.3531	1
48	1.1606	1
33,30,47	1.0653	3	1.03
44,45	0.9643	2

¹³C NMR Spectra of Molecule 18

13C NMR Spectra of Molecule 18 Full Spectra	13C NMR Spectra of Molecule 18 Truncated Spectra

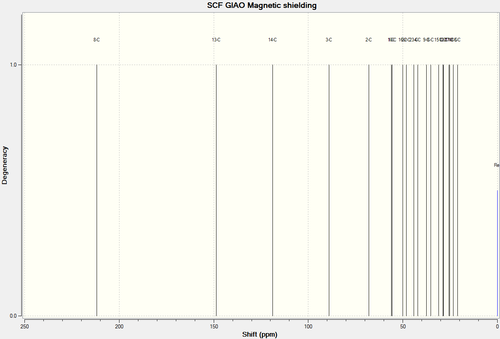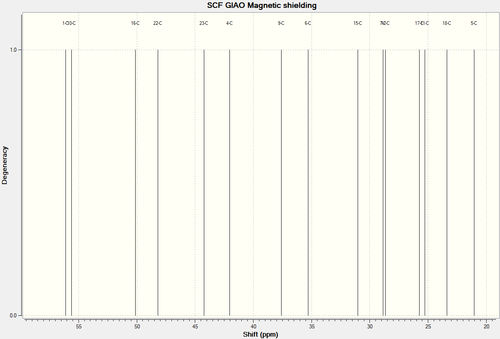C-Atoms	Chemical Shift (ppm)	Integration Height/Degeneracy	Literature Values
8	211.8325	1	211.49
13	148.6673	1	148.72
14	118.8373	1	120.90
3	89.0869	1	74.61
2	67.8886	1	60.53
1	56.1133	1	51.30
10	55.5998	1	50.94
16	50.1124	1	45.53
22	48.2030	1	43.28
23	44.2222	1	40.82
4	42.0354	1	38.73
9	37.5865	1	36.78
6	35.3106	1	35.47
15	31.0459	1	30.84
7	28.8476	1	30.00
12	28.6623	1	25.56
17	25.7393	1	25.35
11	25.2603	1	22.21
18	23.3944	1	21.39
5	21.0478	1	19.83

Part 4 : Analysis of the Properties of the Synthesized Alkene Epoxides

The two catalytics systems

Assymmetric epoxidation of prochiral alkenes may lead to product with different stereochemical outcome as illustrated as below. To solve this problem, different types of asymmetric epoxidation catalyst have been synthesized. In this study, we shall be focusing on Shi asymmetric fructose catalyst as well as Jacobsen asymmetric catalyst.

The Shi Asymmetric Fructose Catalyst

Molecule 21 is the stable precursor of molecule 22, the active catalyst. Molecule 21 can be converted to molecule 22 by using either persulfuric acid or potassium peroxymonosulphate.

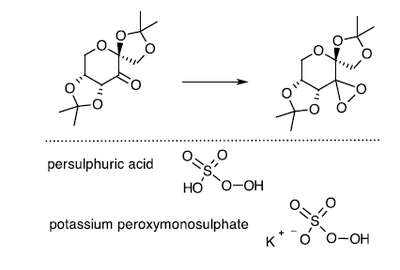
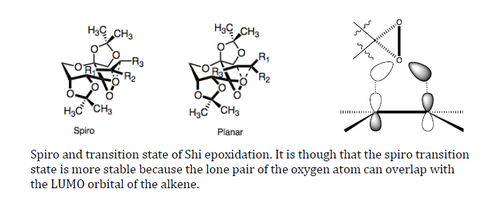
The transition state of the Shi epoxidation was a subject of debate for a few moments. However, recent studies have led to the conclusion that the spiro transition state is more favored than the planar transition state. The spiro transition state is the transition that has its dioxirane perpendicularly bisecting the alkene double bond. This is thought to be more favourable due to interactions between the lone pairs of the oxygen with the LUMO of the alkene.

The Jacobsen Asymmetric Catalyst

Molecule 23 is the stable precursor of molecule 24, the active catalyst. Molecule 23 can be converted to molecule 24 by using sodium perchlorate.

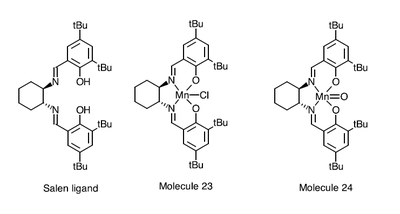
Jacobsen catalyst is biphasic. The first phase involves the transfer of oxygen to molecule 23. Sodium perchlorate oxidizes Mn(III) to Mn(V).

In the second step, Jacobsen catalyst acts via a radical mechanism. It is thought to be so because epoxidation of trans-alkene by Jacobsen catalyst yield cis-alkene as well. A radical mechanism will lead to the lost of stereochemical information of the molecule.

Crystal structure of the two catalyst

Molecule 21

Analysis of Crystal Structure of Molecule 21
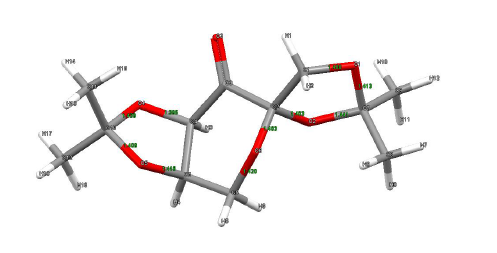Bond	Bond Lenghts (Angstrom)	Evaluation
O1-C1	1.400	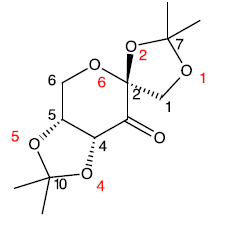The normal bond length of an C-O bond is 1.430 angstrom. The most interesting aspect here is O4 and O2. The lone pair of O4 is antiperplanar to the sigma* orbital of the carbonyl group while the lone pair of O2 is anti periplanar to the carbonyl pi* orbital. Donation of electron can occur because of the correct symmetry. Due to the mixing of the orbitals, the C2-O2 and C4-O4 has been conferred with a certain degree of double bond character. However, due to the lone pair on oxygen being now donated to the carbonyl antibonding orbitals, the O2 and O4 is slightly “electron deficient” and electron density will be pulled away from O2 and O4. That would explain why the bond length increase for O2-C7 and O4-C10. Increase in bond length is an indicator of the weakening of the bond.
O1-C7	1.413
O2-C7	1.441
O2-C2	1.403
O4-C4	1.396
O4-C10	1.439
O5-C10	1.409
O5-C5	1.416
O6-C2	1.403
O6-C6	1.420

Molecule 23

Analysis of Crystal Structure of Molecule 23

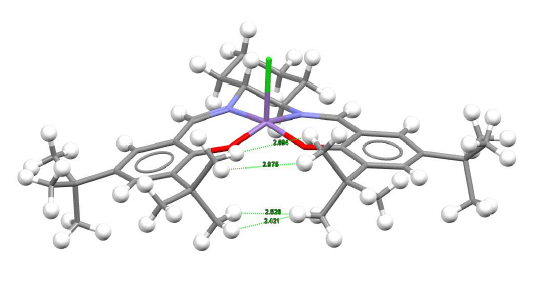The most outstanding feature from this molecule is the fact that is adopt a puckered form of the square base pyramidal form. This is no surprise that the molecule is almost planar due to the electron delocalization around each side of the salen ligand. The tery-butyl hydrogen are oriented closely to one another. Non-covalent interaction studies indicated that repulsion would occur for H---H bond length that are less than 2.1 angstrom while favourable interaction may be dominant with bond length above 2.4 angstrom. It was discovered that all 4 hydrogens have bond length more than 2.4 angstrom hence there should not be any significant repulsion between them. Instead, certain amount of attractive force will ensue and that contributes to the overall stability of the molecule

The calculated NMR properties of the product

The two products that have been chosen are styrene and trans-stilbene.

	(R)-Styrene	(S)-Styrene
1H NMR data	Shift (ppm) Degeneracy 7.4891704929 4.0000 7.2988172444 1.0000 3.6627082199 1.0000 3.1170156088 1.0000 2.5382383043 1.0000	Shift (ppm) Degeneracy 7.4892967873 4.0000 7.2987138125 1.0000 3.6632689921 1.0000 3.1151709109 1.0000 2.5339209685 1.0000
1H NMR Spectra
13C NMR data	Shift (ppm) Degeneracy 135.1098747604 1.0000 124.1186533632 1.0000 123.4150641684 1.0000 122.9584694331 2.0000 118.2653162569 1.0000 54.0265785300 1.0000 53.4853575062 1.0000	Shift (ppm) Degeneracy 135.1323742030 1.0000 124.1343038829 1.0000 123.4137039868 1.0000 122.9558208084 2.0000 118.2690258882 1.0000 54.0599580762 1.0000 53.4684920923 1.0000
13C NMR Spectra
	(R,R)-Trans-stilbene	(S,S)-Trans-stilbene
1H NMR data	Shift (ppm) Degeneracy 7.5705724829 2.0000 7.4791732656 8.0000 3.5390102503 2.0000	Shift (ppm) Degeneracy 7.5705651164 2.0000 7.4791779628 8.0000 3.5374502607 2.0000
1H NMR Spectra
13C NMR data	Shift (ppm) Degeneracy 134.0942417727 2.0000 124.2206838184 2.0000 123.5192390024 2.0000 123.2125901307 2.0000 123.0785800542 2.0000 118.2583039589 2.0000 66.4212770637 2.0000	Shift (ppm) Degeneracy 134.0899175142 2.0000 124.2224499528 2.0000 123.5180152862 2.0000 123.2113538650 2.0000 123.0745448885 2.0000 118.2635789492 2.0000 66.4249347217 2.0000
13C NMR Spectra

Assigning the absolute configuration of the product

The two products that have been chosen are styrene and trans-stilbene.

	(R)-Styrene	(S)-Styrene	(R,R)-Trans-stilbene	(S,S)-Trans-stilbene
Predicted ORP	-24 deg	32.1 deg	296 deg	-205.2 deg
Experimental ORP	-24 deg	32.1 deg	296 deg	-205.2 deg
Experimental conditions	1.00g/100ml, chloroform, 21 degree Celcisus, 589 nm wavelength	1.02g/100ml (99% ee), chloroform, 25 degree Celsius, 589 nm wavelength	1.01g/100ml, ethanol, 22 degree Celsius, 589 nm wavelength	0.6g/100ml, ethanol, 20 degree Celsius, 589 nm wavelength
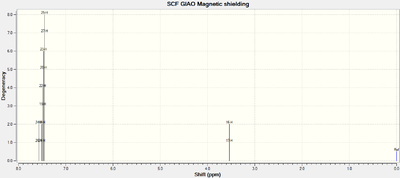
Predicted VCD Spectrum

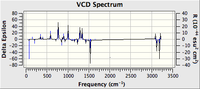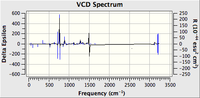All the assignments given in the literature reports are correct although the predicted value differs slightly with the experimental values

Analysis of the Transition State for Reactions

Predicting Enantiomeric Excess based on Transition State energies

One of the energy output from Gaussian calculation is the “sum of electronic and thermal free energies”. This is Gibbs Free Energy at 298.15K and 1 atm.

Using this term and invoking a variant of the Curtin-Hammett Principle, it is possible to calculate a predicted enantiomeric excess of one enantiomer over the other.

Using the derivations from above and equation (4), we analyze the enantiomeric excess of beta-methyl styrene and the results are tabulated as below:

Free Energy of (R,R) transition state	Free Energy of (S,S) transition state	Difference in free energies (Hartrees)	K	Enantiomeric Excess (%)
-1343.022970	-1343.017942	-0.005028	4.88E-03	99.03
-1343.019233	-1343.015603	-0.003630	2.14E-02	95.80
-1343.029272	-1343.023766	-0.005506	2.94E-03	99.41
-1343.032443	-1343.024742	-0.007701	2.88E-04	99.94

The above hartree units are converted to J/mol for calculation of K where 1 hartress = 4.3597E-18

Studying all the free energies of the (R,R) series and compare them with the (S,S) series, it comes as no surprise that (R,R) product is favoured over (S,S) product as (R,R) is more stable. Indeed, this corresponds with the literature value reporting 92% ee of (R,R) products over that of (S,S).

Shi Fructose Catalyst

For this section, I will be analyzing the the transition state of 1) styrene and 2) trans-stilbene with the Shi fructose catalyst.

(R) and (S)-styrene transition state

The transition state for the formation of (R)-styrene oxide and (S)-styrene oxide are given as below:

	(R)-styrene oxide	(S)-styrene oxide
Structure of Catalyst	test molecule	test molecule
Approach of ligand

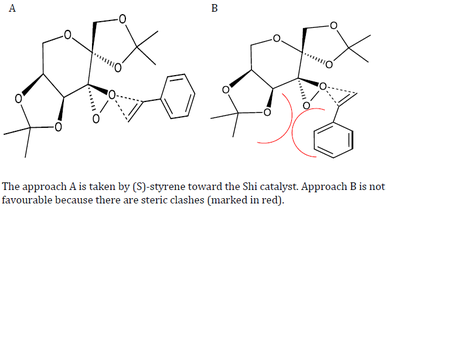In the transition state for (R)-styrene, it was discovered that the Re face is reacting with the oxygen of the dioxirane. The phenyl ring is oriented endo with respect to the fructose catalyst. However, the (S)-styrene is reacting at the Si face and the phenyl ring is oriented exo relative to the catalyst.

The approach taken by (R)-styrene and (S)-styrene are restricted to only one due to steric interactions. Therefore, the epoxidation of both styrenes by the Shi catalyst will be stereospecific and retains all the stereochemical information of the reactant. However, whether or not (R)-styrene oxide or (S)-styrene oxide is form is dependent on the relative energies of the transition state. The more stable the transition state, the more likely the product of the transition state will be formed.

So in order to examine this, an example of transition state of both styrenes with Shi catalyst are obtained and analyzed.

Free Energy of (R,R) transition state	Free Energy of (S,S) transition state	Difference in free energies (Hartrees)	K	Enantiomeric Excess (%)
-1303.736813	-1303.727673	-0.00914	6.28E-05	99.99

From the above, we can see the predicted high enantiopurity of the reaction favoring the (R) product because of the lower energy of the transition states. To understand the reason, we have to turn to non-covalent interaction (NCI) analysis.

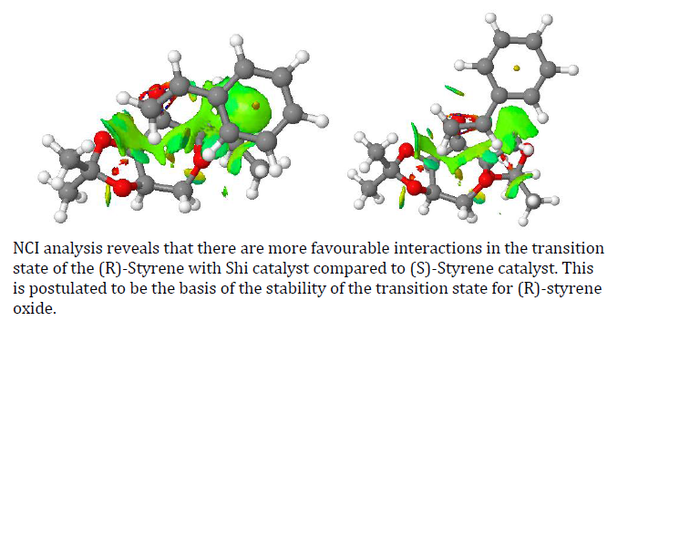
To complement the NCI analysis, a QTAIM (Quantum Theory of Atoms in Molecules) analysis is conducted as well.

(R)-styrene transition state	(S)-styrene transition state
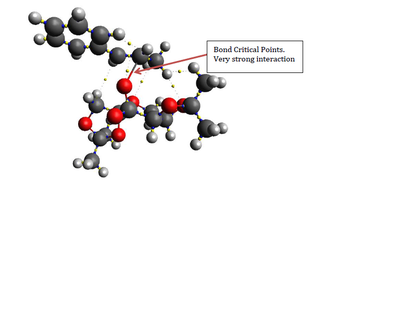Comments
Unsurprisingly, QTAIM analysis has also shown that (R)-styrene/Shi catalyst has more interactions with one another. While (R)-styrene has 2 strong interactions, (S)-styrene has only one with the catalyst. Besides, the phenyl ring of (R)-styrene also confers additional positive interaction with the catalyst. QTAIM analysis has also show several interactions between the C=C geminal hydrogen of (R)-styrene intreacting with the oxygen atoms on the dioxacyclopentane ring

(R,R) and (S,S)-Stilbene transition state

	(R,R)-Stilbene oxide	(S,S)-Stilbene oxide
Structure of Transition State	test molecule	test molecule
Approach of ligand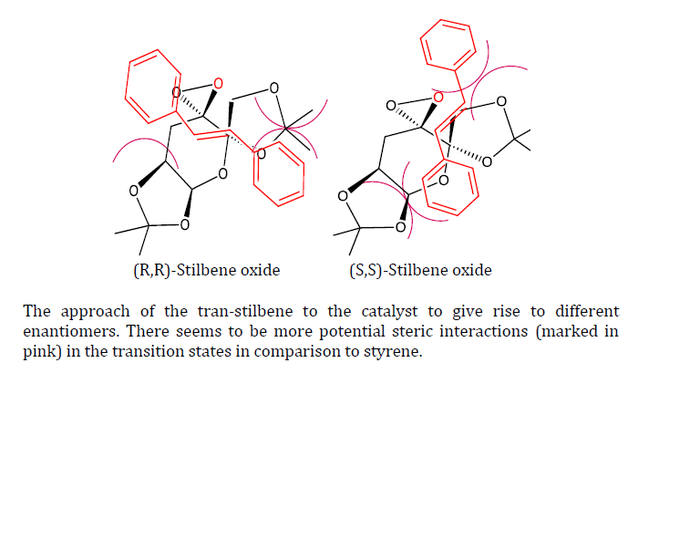

However, unlike styrene, trans-stilbene seems to approach perpendicularly to the dioxirane. This is proposed to be due to the steric interactions (marked in purple). Based on first inspection, it seems that (S,S)-Stilbene oxide has more steric interactions than (R,R)-Stilbene oxide. Although unsubstantial, it seems like my guess was correct. The (R,R)-stilbene/Shi catalyst transition state is lower in energy.

Free Energy of (R,R) transition state	Free Energy of (S,S) transition state	Difference in free energies (Hartrees)	K	Enantiomeric Excess (%)
-1534.687808	-1534.683440	0.004368	9.08E-3	98.20

NCI Analysis is also done for trans-stilbene

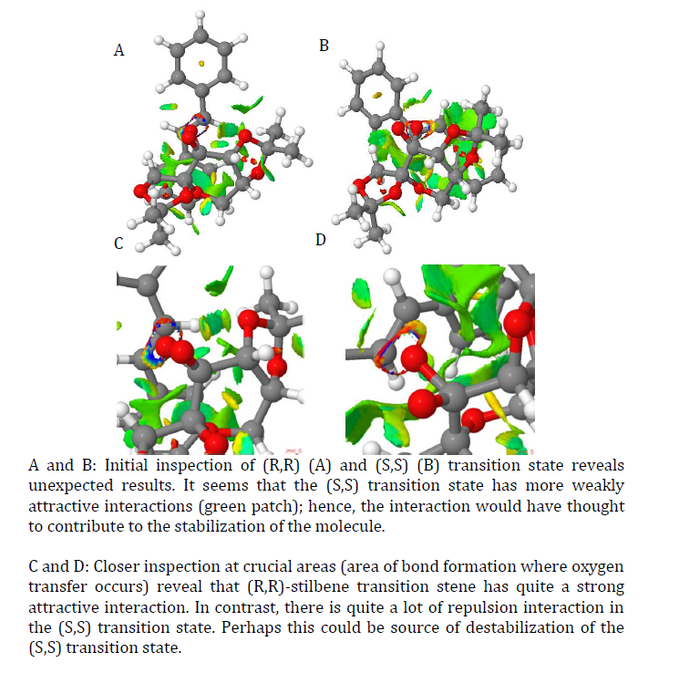
Jacobsen Catalyst

For this section, cis-beta methyl styrene transition state will be analyzed.

Free Energy of (R,R) transition state	Free Energy of (S,S) transition state	Difference in free energies (Hartrees)	K	Enantiomeric Excess (%)
-3383.259559	-3383.251060	-0.008499	1.24E-04	99.98
-3383.253442	-3383.250270	-0.003172	3.48E-02	93.27

As is obvious from here, the (S,R) transition state is more stable than the (R,S) transition state. Both transition states are exo with respect to the catalyst.

It is not immediately apparent just by looking at the molecule to determine which spatial groups have interactions with one another. Therefore, an NCI analysis is conducted again.

Bibliography

1. David C. Forbes, Sampada V. Bettigeri,Samit A. Patrawala, Susanna C. Pischek, and Michael C. Standen, Tetrahedron, 2009, 65(1), 70-76

2. Hui Lina, Jing Qiaoa, Yan Liua, Zhong-Liu Wu, Journal of Molecular Catalysis B: Enzymatic, 2010, 67, 236-241

3. Niwa,Takashi, Nakada,Masahisa, Journal of the American Chemistry , 2012, 134, 13538-13541

4. Arlette Solladié-Cavallo, Anh Diep-Vohuule, Tetrahedron: Asymmetry, 1996, 7(6), 1783-1788

5. Vito Capriati, Saverio Florio, Renzo Luisi,Filippo Maria Perna, Antonio Salomone, Francesco Gasparrini, Org. Lett., 2005, 7 (22), 4895-4898

6. Wong O.Andrea, Wang Bin, Zhao Mei-Xin, Shi Yian, Journal of Organic Chemistry, 2009, 74, 6335-6338

7. Alan B. McEwen, Paul v. R. Schleyer, Journal of The American Chemical Society, 2002, 108(4), 250-253

8. Halgren T. A. J. Comput. Chem., 1999, 20, 720-729.

9. J. Hanson,J. Chem. Educ., 2001, 78, 1266