Rep:Mod:Complabreport SiyaVij
NH3 Molecule
NH3 |
Summary Table
| Molecule Name | NH3 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| E(RB3LYP) | -56.5578 au |
| RMS Gradient Norm | 0.00000485 |
| Point Group | C3V |
| Optimized N-H bond distance | 1.01798 angstrom |
| Optimized H-N-H bond angle | 105.741 |
Item Table
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
The optimization file is linked to here
Vibrations Table
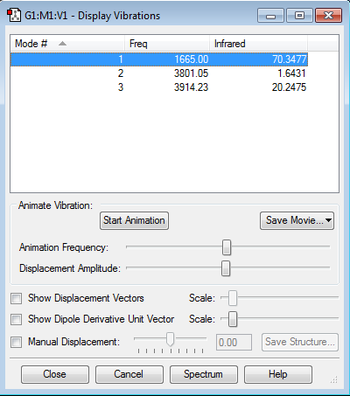
Vibrations active at 0 Kelvin for optimized NH3 Molecule:
The table above confirms that there are no negative frequencies for this molecule.
We expect 6 different modes from the 3N-6 rule as there are 4 atoms in the molecule(N=4). Modes 2 and 3 have the same energy as each other, and modes 5 and 6 are also degenerate in relation to one another. Modes 1, 2 and 3 are bending vibrations and modes 4, 5 and 6 are bond stretch vibrations. Mode 4 is highly symmetric. Mode 1 is known as the 'umbrella' mode. We would expect to see 4 bands in an experimental spectrum of gaseous ammonia as modes 2 and 3 and modes 5 and 6 are degenerate pairs. However, as shown by the infrared values only modes 1-3 have a high enough intensity to show up on the spectrum. Therefore only 2 modes are observed which are mode 1 and mode 2/3 (as modes 2 and 3 are degenerate).
Charges
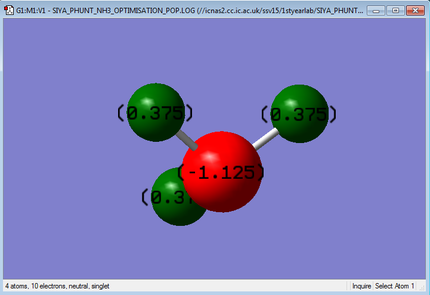
The charges present on the atoms of the NH3 molecule are displayed in the image below:
A charge of -1.125 au on the Nitrogen atom and a charge 0.375 au of on the Hydrogen atoms is expected because nitrogen is more electronegative and so draws electron density towards itself, therefore producing a more negative charge. The charges observed in the GaussView program are the ones we expect.
N2 Molecule
N2 |
Summary Table
| Molecule Name | N2 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| E(RB3LYP) | -109.524 au |
| RMS Gradient Norm | 0.00000060 |
| Point Group | D*H |
| Optimized N-N bond distance | 1.10550 angstrom |
Item Table
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
The optimization file is linked to here
Vibrations Table
Vibrations active at 0 Kelvin for optimized N2 Molecule:
The table above confirms that there are no negative frequencies for this molecule.
The 3N-5 rule is used instead of the 3N-6 rule for the N2 molecule, as its a linear molecule. According to this rule, the number of modes expected is 1. The mode shown is a symmetrical bond stretch.
H2 Molecule
H2 |
Summary Table
| Molecule Name | H2 |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| E(RB3LYP) | -1.17853936 au |
| RMS Gradient Norm | 0.00000017 |
| Point Group | D*H |
| Optimized H-H bond distance | 0.74279 angstrom |
Item Table
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
The optimization file is linked to here
Vibrations Table
Vibrations active at 0 Kelvin for optimized H2 Molecule:
The table above confirms that there are no negative frequencies for this molecule.
Haber-Bosch Process
Reaction
N2 + 3H2 -> 2NH3
Energies
E(NH3)= -56.55776762 au
2*E(NH3)= -113.11553524 au
E(N2)= -109.52412868 au
E(H2)= -1.17853936 au
3*E(H2)= -3.53561808 au
ΔE=2*E(NH3)-[E(N2)-3*E(H2)]= -146.980542156 kJ/mol
The product, NH3 is more stable than the reactants, (N2) and (H2) as the reactants are lower in energy. This means the forward reaction is more energetically favourable, also shown by the negative sign on the overall energy, -146.98 kJ/mol (2d.p.).
H2O Molecule
H2O |
Summary Table
| Molecule Name | H2O |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d.p) |
| E(RB3LYP) | -76.41973740 au |
| RMS Gradient Norm | 0.00006276 |
| Point Group | C2V |
| Optimized 0-H bond distance | 0.96522 angstrom |
| Optimized H-O-H bond angle | 103.745 |
Item Table
Item Value Threshold Converged? Maximum Force 0.000099 0.000450 YES RMS Force 0.000081 0.000300 YES Maximum Displacement 0.000128 0.001800 YES RMS Displacement 0.000120 0.001200 YES
The optimization file is linked to here
Vibrations Table
Vibrations active at 0 Kelvin for optimized H2 Molecule:
The table above confirms that there are no negative frequencies for this molecule.
According to the 3N-6 rule, we expect there to be 3 modes of vibration for the H2O molecule. All 3 modes have different energies to one another. Modes 2 and 3 shown in the table are stretching vibrations and mode 1 is a bending vibration. Mode 2 is symmetric. As none of the modes are degenerate we expect to see 3 bands shown in an experimental spectrum of H2O.
Charges
The charges on the atoms of the water molecule meet our expectations, as the oxygen atom is more electronegative than the hydrogen atoms. Therefore it draws electron density towards itself and has a negative charge of -0.944 au, whereas the hydrogen atoms have a positive charge of 0.472 au.
Molecular Orbitals
MO 1-5 are occupied molecular orbitals and MO 7 is the only unoccupied orbital shown imaged above. MO 1 is the lowest in energy, -19.13799 au, and is a lot lower in energy than the others. This is due to molecular orbital being formed from the 1s orbital of the oxygen atom and therefore the molecular orbital remains very closely packed around the oxygen nuclei. MO 2 is formed from the 1s and 2s orbitals and therefore is mostly symmetrical. MO 3-7 are a combination of the 2p orbitals from oxygen and the 1s orbitals from the hydrogen atoms. The highest occupied molecular orbital (HOMO) is MO 5 and consists of the 2px orbital and the 1s orbital. MO 7 is an anti-bonding orbital. The shapes of higher unoccupied molecular orbitals were not chosen as they are more unreliable.