Rep:Mod:Complabnumber3
NH3 molecule
Physical Properties
N-H bond distance = 1.02 Å
H-N bond angle = 106°
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
NH3 (Ammonia) |
| Optimisation Data NH3 | |
|---|---|
| Molecule name | NH3 (Ammonia) |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(D,P) |
| Final energy / au | -56.558 |
| RMS gradient / au | 0.00000485 |
| Point group symmetry | C3v |
Vibrational Modes
| Vibration | Wavenumber / cm-1
(to nearest whole integer) |
Intensity
(to nearest whole integer) |
Symmetry |
|---|---|---|---|
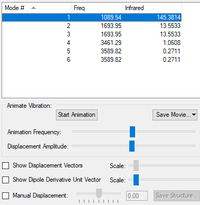
| 1 | 1090 | 145 | A1 |
| 2 | 1694 | 14 | E |
| 3 | 1694 | 14 | E |
| 4 | 3461 | 1 | A1 |
| 5 | 3590 | 0 | E |
| 6 | 3590 | 0 | E |
Ammonia has 4 atoms, so from the 3N-6 rule, there are 6 expected modes of vibration, which can be seen to be true in the table above. There are two sets of these vibration modes which are degenerate, two with wavenumber 1694 cm-1 and two with 3590 cm-1 . The "bending" vibrations are the three with the lower wavenumbers, 1090 cm-1 and the two 1694 cm-1 , while the other three "bond stretch" vibrations have higher wavenumbers 3461 cm-1 and the two 3590 cm-1 . The "bond stretching" vibration at 3461 cm-1 is highly symmetric as all three bonds are vibrating in and out together. The mode known as the "umbrella" mode is a symmetric bend with wavenumber 1090 cm-1 . Due to there being 2 degenerate vibration modes, you would expect to see 4 bands in an experimental spectrum of gaseous ammonia.
Charge Analysis
Electronegativity refers to an atoms ability to attract a bonding pair of electrons. In ammonia the Nitrogen is more electronegative than the Hydrogen. Therefore it would be expected the Nitrogen to attract the electrons more strongly and so have a slightly negative charge, while the hydrogens will have a slightly positive charge. Given the overall molecule is neutral, the sum of the positive charge on each H will be equal to the magnitude of the negative charge on the N. From analysis of the charge distribution, the charge on the Nitrogen is -1.125 and the charge on each Hydrogen is 0.375.
H2 and N2
H2
Physical Properties
H-H bond distance = 0.74 Å However when acting as ligands in transition metal complexes the bond length is extended to around 0.81 Å.
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
H2 (Hydrogen) |
| Optimisation Data H2 | |
|---|---|
| Molecule name | Hydrogen |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(D,P) |
| Final energy / au | -1.179 |
| RMS gradient / au | 0.00000017 |
| Point group symmetry | D∞h |
Vibrational modes
| Vibration | Wavenumber cm-1 (to nearest whole integer) | Intensity
(to nearest whole integer) |
Symmetry |
|---|---|---|---|
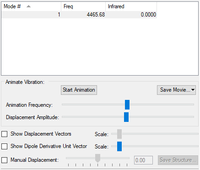
| 1 | 4466 | 0 | SGG |
H2 is a linear molecule and so should have 3N-5 number of vibrational modes for N number of atoms. There are 2 atoms and so should be 1 vibrational mode, which can be seen in the table above. This is a "bond stretch" vibrational mode.
Charge Analysis
The two atoms have equal electronegativity and so have 0.00 charge each.
N2
Physical Properties
N-N bond distance = 1.11 Å
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
N2 (Nitrogen) |
| Optimisation Data N2 | |
|---|---|
| Molecule name | Nitrogen |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(D,P) |
| Final energy / au | -109.524 |
| RMS gradient / au | 0.00000060 |
| Point group symmetry | D∞h |
Vibrational modes
| Vibration | Wavenumber cm-1 (to nearest whole integer) | Intensity
(to nearest whole integer) |
Symmetry |
|---|---|---|---|
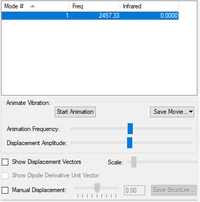
| 1 | 2457 | 0 | SGG |
N2 is a linear molecule and so should have 3N-5 number of vibrational modes for N number of atoms. There are 2 atoms and so should be 1 vibrational mode, which can be seen in the table above. This is a "bond stretch" vibrational mode.
Charge Analysis
The two atoms have equal electronegativity and so have 0.00 charge each.
Haber-Bosch Process
| Haber-Bosch energy change calculation | Energy / kjmol-1 |
|---|---|
| E(NH3 ) | -148493.0 |
| 2*E(NH3 ) | -296986.1 |
| E(N2 ) | -287492.3 |
| E(H2 ) | -3095.5 |
| 3*E(H2 ) | -9286.4 |
| ΔE of reaction | -207.4 |
The overall energy change of the reaction is negative, making it weakly exothermic. From this we can tell that the product, in this case NH3, is most stable than the sum of it's gaseous reactants (H2 and N2).
Project molecule: CO2
Physical Properties
O=C bond distance = 1.17 Å
O=C bond angle = 180°
Item Value Threshold Converged? Maximum Force 0.000024 0.000450 YES RMS Force 0.000017 0.000300 YES Maximum Displacement 0.000021 0.001800 YES RMS Displacement 0.000015 0.001200 YES
CO2 (Carbon Dioxide) |
| Optimisation Data CO2 | |
|---|---|
| Molecule name | CO2 Carbon Dioxide |
| Calculation type | FREQ |
| Calculation method | RB3LYP |
| Basis set | 6-31G(D,P) |
| Final energy / au | -188.581 |
| RMS gradient / au | 0.0000115 |
| Point group symmetry | D∞h |
Vibrational Modes
| Vibration | Wavenumber / cm-1
(to nearest whole integer) |
Intensity
(to nearest whole integer) |
Symmetry |
|---|---|---|---|
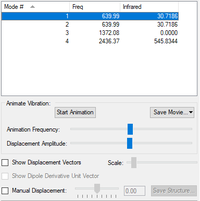
| 1 | 640 | 31 | PIU |
| 2 | 640 | 31 | PIU |
| 3 | 1372 | 0 | SGG |
| 4 | 2436 | 546 | SGU |
Carbon Dioxide has 3 atom but is linear, so from the 3N-5 rule, there are 4 expected modes of vibration, which can be seen to be true in the table above. There are two modes which are degenerate at 640 cm-1 . These are "bending" vibrations, while the other two, at 1372 cm-1 and 2436 cm-1 are "bond stretch" vibrations.
Charge Analysis
Electronegativity refers to an atoms ability to attract a bonding pair of electrons. In carbon dioxide the oxygen is more electronegative than the carbon. Therefore it would be expected that the oxygen would attract the electrons more strongly and so have a slightly negative charge, while the carbon will have a slightly positive charge. Given the overall molecule is neutral, the sum of the magnitude of the charges on each O will be equal to the the positive charge on the C. From analysis of the charge distribution, the charge on each of the oxygen is -0.511 and the charge on the carbon is 1.022.
Molecular Orbitals
The following table shows four of the molecular orbital diagrams for CO2, in order of increasing energy.
| Diagram | MO |
|---|---|
|
CO2 MO, 1σg |
|
CO2 MO, 1σu |

|
Bonding MO, 2σu |

|
Bonding MO, 1πu |
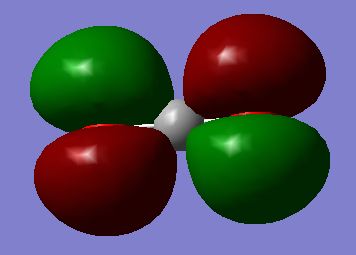
|
Non-bonding MO, 1πg |
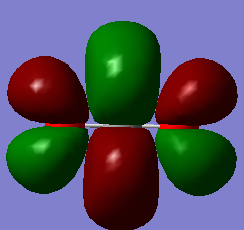
|
Anti-bonding MO, 2πu |
Marking
Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.
Wiki structure and presentation 1/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES
NH3 0.5/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
NO
Have you included answers to the questions about vibrations and charges in the lab script?
YES - you correctly explained how the degenerate modes are influencing the number of expected bands. But you missed to interpret the intensities of the calculated vibrations. This would have decreased the number of expected bands to two as the stretching vibrations are too low in energy to be observed experimentally.
N2 and H2 0.5/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES
Crystal structure comparison 0/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
NO - you only state a value for a H2 transition metal complex without giving any reference.
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 0.5/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
NO - The right value is 146.5kJ/mol instead.
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES - even though the calculated reaction energy is wrong you concluded the product to be more stable correctly.
Your choice of small molecule 2.5/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
YES - the analysis of the calculated vibrations and charges is good! You could have analysed the MOs in more depth. You correctly stated the contribution to bonding except for the first two MOs which are non-bonding. For the next time you should but missed to comment on relative energies, contributing AOs and the occupancy.
Independence 0/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or Do some deeper analysis on your results so far
NO - no independent work has been identified.
