Rep:Mod:Clarachong

NH₃ molecule

General Information

NH₃ Ammonia

Calculation Type

OPT, FREQ

Calculation Method

RB3LYP

Basis Type

6-31G(D,P)

RMS gradient (a.u.)

0.00000485

Final energy E (a.u.)

-56.5577687

Point group

C_3v

N-H bond length

1.018

N-H bond angle

105.74

Obtain the optimisation file here

Optimising the molecule: Item table

        Item               Value     Threshold  Converged?
Maximum Force            0.000004     0.000450     YES
RMS     Force            0.000004     0.000300     YES
Maximum Displacement     0.000072     0.001800     YES
RMS     Displacement     0.000035     0.001200     YES
Predicted change in Energy=-5.986274D-10

Vibrational modes of NH₃

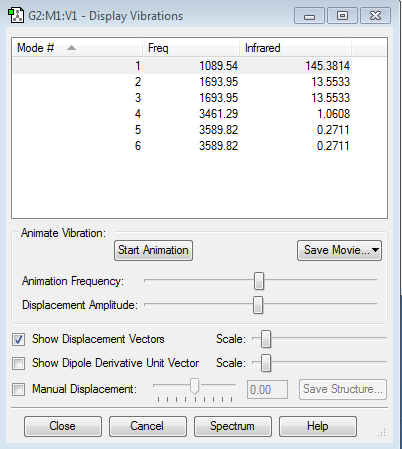
A screenshot of the different modes of vibrations in a NH₃ molecule.

Expected number of modes	3N-6 = 3(4)-6 =6
Number of degenerate modes	Modes 2 and 3 Modes 5 and 6
"Bending" vibrations	Modes 1,2,3
"Bond stretch" vibrations	Modes 4,5,6
Umbrella mode	Mode 1
Highly symmetric mode	Mode 4
Number of bands expected to be observed	Even though there are 4 distinct modes, only 2 of them (Mode 1 and degenerate modes 2 and 3) will be observed. This is because the IR intensity of modes 4,5 and 6 (reflected on the right most row) are too low to be seen and will disappear on the IR spectrum.

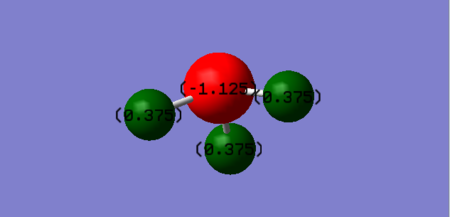
Atomic charges of NH₃

Atom	Charge
Hydrogen	+0.375
Nitrogen	-1.125

Nitrogen is expected to carry a negative charge as it is more electronegative compared to the neighbouring Hydrogen atoms. Hence, due to Nitrogen's larger electronegativity value, the electrons will be situated nearer the Nitrogen atom, causing it to take on a negative charge.

N₂ molecule

General Information

N₂ molecule

Calculation Type

OPT, FREQ

Calculation Method

RB3LYP

Basis Type

6-31G(D,P)

RMS gradient (a.u.)

0.00000060

Final energy E (a.u.)

-109.52412868

Point group

D_∞h

N-H bond length

1.10550

Obtain the optimisation file link here

Optimising the molecule: Item table

Item               Value     Threshold  Converged?
Maximum Force            0.000001     0.000450     YES
RMS     Force            0.000001     0.000300     YES
Maximum Displacement     0.000000     0.001800     YES
RMS     Displacement     0.000000     0.001200     YES
Predicted change in Energy=-3.401076D-13

Vibrational modes of N₂

Frequency	Infrared
2457.33	0.0000

Since both nitrogen atoms are identical, the molecule does not have a dipole moment and hence will not be detected by IR spectroscopy, giving a infrared reading of zero.

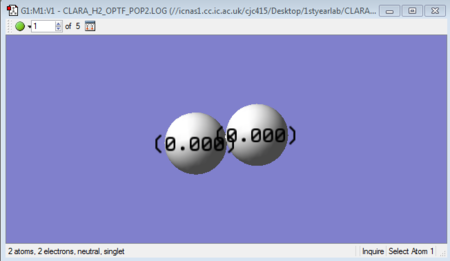
Atomic charges of N₂

Atom	Charge
Nitrogen	0.000

Since both Nitrogen atoms are identical and indistinguishable, both atoms do not carry any charge.

Molecular orbitals of N₂

When 2 atoms react to form a molecule, the number of molecular orbitals (MO) in the molecule will be a linear combination of the number of atomic orbitals (AO) of each atom. The total number of electrons in the MO diagram will be the total number of electrons of each atom. Since Nitrogen has a 7 electrons with an electronic configuration of 1s²2s²2p³, the N₂ molecule has a total of 14 electrons, with each p electron involved in 1 sigma and 2 pi bonds.

Reactions often involve the highest energy electrons, located in the highest energy molecular orbital (HOMO). Electrons that are donated to the molecule will be located at the lowest possible energy level, known as the lowest energy unoccupied molecular orbital (LUMO). Shown in the table below are diagrams of the HOMO and LUMO of N₂.

HOMO	LUMO

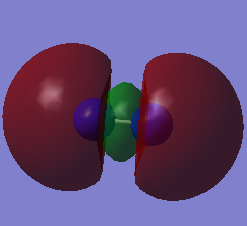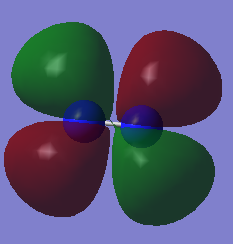
H₂ molecule

General Information

H₂ molecule

Calculation Type

OPT, FREQ

Calculation Method

RB3LYP

Basis Type

6-31G(D,P)

RMS gradient (a.u.)

0.00000017

Final energy E (a.u.)

-1.17853936

Point group

D_∞h

N-H bond length

1.10550

Obtain the optimisation file link here

Optimising the molecule: Item table

        Item               Value     Threshold  Converged?
Maximum Force            0.000000     0.000450     YES
RMS     Force            0.000000     0.000300     YES
Maximum Displacement     0.000000     0.001800     YES
RMS     Displacement     0.000001     0.001200     YES
Predicted change in Energy=-1.164080D-13

Vibrational modes of H₂

Frequency	Infrared
4465.68	0.0000

Similar to N₂, H₂ is not IR active as it does not have a dipole moment and no change in dipole is observed in the symmetric stretch.

Comparing both H₂ and N₂ molecules, it can be observed that the frequency of the H₂ symmetric stretch is higher. Frequency of vibration is inversely proportional to the reduced mass of the molecule and proportional to bond strength.

Molecule	Bond strength/KJmol^-1 _[1]	Reduced mass/a.u.
H₂	436	0.5
N₂	945	7

It can be observed from the table above that the bond strength of N₂ is around twice of H₂ as N₂ has a bond order of 3 (triple bond) compared to H₂ which only has a bond order of 1 (single bond). However, N₂ has a reduced mass 14 times that of H₂. The effect due to the difference in reduced mass outweighs that of bond strength. Since reduced mass and frequency of vibration are inversely proportional, the stretching frequency of N₂ is much lower.

Atomic charges of H₂

Atom	Charge
Hydrogen	0.000

Since both Hydrogen atoms are identical and indistinguishable, both atoms do not carry any charge.

Molecular orbitals of H₂

Similar to the MO diagram shown for N₂, the table below shows the HOMO and LUMO for H₂. Since Hydrogen has an electronic configuration of 1s¹, there will only be 2 electrons in the MO diagram, where the sigma bond is formed.

HOMO	LUMO

The Haber-Bosch process

N₂ + 3H₂ $\to$ 2NH₃

All data recorded in the table below is in a.u.

E(NH₃)	-56.55776873
2*E(NH₃)	-113.11553746
E(N₂)	-109.52412868
E(H₂)	-1.17853936
3*E(H₂)	-3.53561808
ΔE=2E(NH₃)-[E(N₂)+3E(H₂)]	-0.0557907

Hence, ΔE (KJmol^-1) = -0.0557907 x 2625.5 = -146.4784829 KJmol^-1
The negative sign on ΔE indicates that energy is being released into the surroundings during the formation of ammonia from nitrogen and hydrogen. This suggests that the products (ammonia) are lower in energy than the reactants, and hence indicating that they are more thermodynamically stable. The forward reaction which produces ammonia would be favoured.

CH₄ molecule

General Information

CH₄ Methane

An optimised image of a tetrahedral methane molecule.

Calculation Type

OPT, FREQ

Calculation Method

RB3LYP

Basis Type

6-31G(D,P)

RMS gradient (a.u.)

0.00003263

Final energy E (a.u.)

-40.52401404

Point group

T_d

Dipole moment

0.0000

C-H bond length

1.09197

C-H bond angle

109.47122

Obtain the optimisation file here

Optimising the molecule: Item table

        Item               Value     Threshold  Converged?
Maximum Force            0.000063     0.000450     YES
RMS     Force            0.000034     0.000300     YES
Maximum Displacement     0.000179     0.001800     YES
RMS     Displacement     0.000095     0.001200     YES
Predicted change in Energy=-2.256037D-08

Vibrational modes of CH₄

CH₄ Methane
Mode 1	Mode 2	Mode 3

Frequency: 1356.20Hz, Infrared: 14.1008	Frequency: 1356.20Hz, Infrared: 14.1008	Frequency: 1356.20Hz, Infrared: 14.1008
Modes 1, 2 and 3 are degenerate bending modes in 3 different orientations (x, y and z axis)
Mode 4	Mode 5	Mode 6

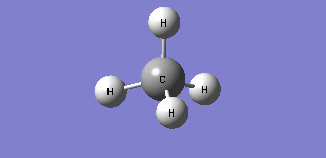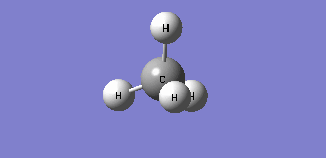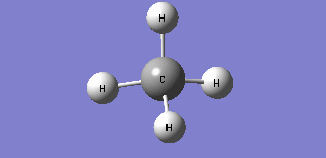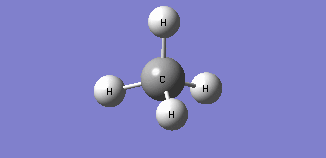
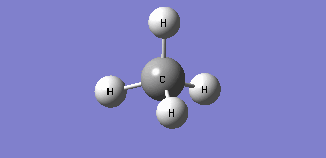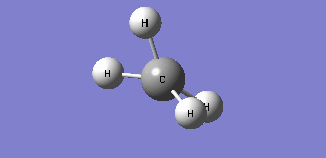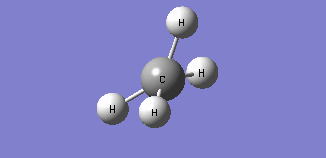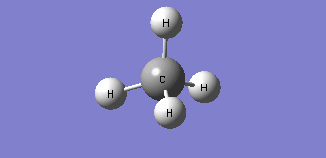
Frequency: 1578.58Hz, Infrared: 0	Frequency: 1578.58Hz, Infrared: 0	Frequency: 3046.46Hz, Infrared: 0
Modes 4 and 5 are degenerate bending modes while mode 6 is a symmetric stretching. Since all 3 modes do not result in a change in dipole moment, they are not IR active.
Mode 7	Mode 8	Mode 9

Frequency: 3162.33Hz, Infrared: 25.3343	Frequency: 3162.33Hz, Infrared: 25.3343	Frequency: 3162.33Hz, Infrared: 25.3343
Modes 7, 8 and 9 are asymmetric stretching modes which are degenerate.
It can be observed that stretching vibrations usually occur at higher infrared intensity levels around 25 compared to bending vibrations at around 14. Since it is easier to bend a bond compared to compressing or stretching it, stretching vibrations occur at higher energy levels and hence result in higher intensity IR readings.

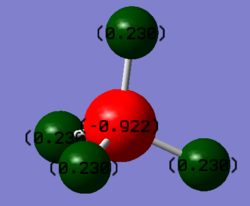
Atomic charges of CH₄

Atom	Charge
Carbon	-0.922
Hydrogen	0.230

As seen from the screenshot above, more electron density can be found on the carbon instead of the hydrogens, causing carbon to take on a partial negative charge. This is because carbon is more the electronegative element. Since methane is a neutral molecule, it can be observed that the sum of the partial positive charges on all the hydrogens are similar to the partial negative charge on carbon.

Molecular orbitals of CH₄

Molecular Orbital	Energy	Comments	MO diagram _[2]
	-10.16707	MO1, the lowest energy 1s bonding orbital surrouding only the central carbon atom. It is not drawn in the MO diagram as it is too low in energy. They contain the two 1s electrons from the carbon atom.
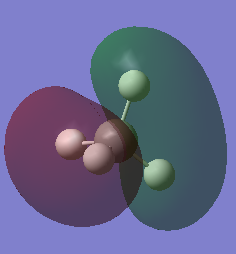	-0.38831	MO3, MO4 and MO5 represent 3 degenerate bonding HOMOs. They represent the bonding 2s orbitals in 3 different orientations (x, y and z axis). They are contributed by the 1s orbitals of the four hydrogen atoms and 2s orbital of the carbon atom.
	0.11842	MO6 represents the LUMO. MO6 is the empty antibonding orbital of MO2. Both MO2 and MO6 are spherical in shape, with MO6 comparatively larger, hence higher in energy.
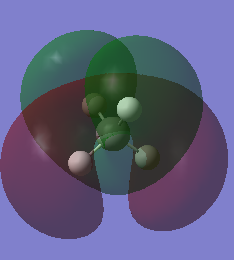	0.17677	MO7, MO8, MO9 represent three degenerate antibonding molecular orbitals in three different orientations. They are antibonding orbitals for bonding orbitals MO3, MO4 and MO5. Compared to MO10, it has fewer nodal regions, hence lower in energy.
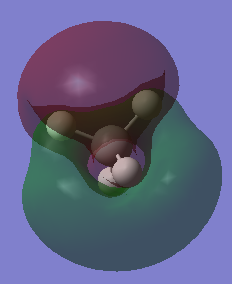	0.52915	MO10 is a high energy antibonding orbital, which is degenerate with MO11 and MO12. (not shown in MO diagram)

CH₃^̹+ and CH₃^̹- ions

General Information

CH₃^̹+ carbocation

CH₃^̹- carboanion

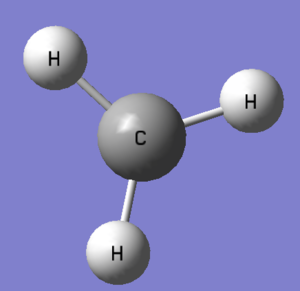
Calculation Type

OPT, FREQ

Calculation Type

OPT, FREQ

Calculation Method

RB3LYP

Calculation Method

RB3LYP

Basis Type

6-31G(D,P)

Basis Type

6-31G(D,P)

RMS gradient (a.u.)

0.00010036

RMS gradient (a.u.)

0.00010504

Final energy E (a.u.)

-39.48468012

Final energy E (a.u.)

-39.79602794

Point group

D_3H

Point group

C_3V

Dipole Moment

0

Dipole Moment

1.7169

Obtain the optimisation file link here

According to the VSEPR theory, the electron deficient postively charged carbocation (3 bond pairs and no lone pairs) will adopt a trigonal planar symmetry shown above.

Unlike the carbocation, the presence of an additional lone pair of electrons on CH₃^̹- will result in a trigonal pyramidal symmetry (similar to ammonia)

Optimising the molecule: Item table

CH₃^̹+

        Item               Value     Threshold  Converged?
Maximum Force            0.000201     0.000450     YES
RMS     Force            0.000131     0.000300     YES
Maximum Displacement     0.000569     0.001800     YES
RMS     Displacement     0.000373     0.001200     YES
Predicted change in Energy=-1.714129D-07

CH₃^̹-

        Item               Value     Threshold  Converged?
Maximum Force            0.000173     0.000450     YES
RMS     Force            0.000114     0.000300     YES
Maximum Displacement     0.000523     0.001800     YES
RMS     Displacement     0.000372     0.001200     YES
Predicted change in Energy=-1.736478D-07

NH3 molecule

General Information

Optimising the molecule: Item table

Vibrational modes of NH3

Atomic charges of NH3

N2 molecule

General Information

Optimising the molecule: Item table

Vibrational modes of N2

Atomic charges of N2

Molecular orbitals of N2

H2 molecule

General Information

Optimising the molecule: Item table

Vibrational modes of H2

Atomic charges of H2

Molecular orbitals of H2

The Haber-Bosch process

CH4 molecule

General Information

Optimising the molecule: Item table

Vibrational modes of CH4

Atomic charges of CH4

Molecular orbitals of CH4

CH3̹+ and CH3̹- ions

General Information

Optimising the molecule: Item table

NH₃ molecule

Vibrational modes of NH₃

Atomic charges of NH₃

N₂ molecule

Vibrational modes of N₂

Atomic charges of N₂

Molecular orbitals of N₂

H₂ molecule

Vibrational modes of H₂

Atomic charges of H₂

Molecular orbitals of H₂

CH₄ molecule

Vibrational modes of CH₄

Atomic charges of CH₄

Molecular orbitals of CH₄

CH₃^̹+ and CH₃^̹- ions