Rep:Mod:Chunyi89
Week 1: Basic calculations & analysis of simple molecules: BH3, TlBr3, BBr3, NH3
BH3 Optimisation (Day 1)
This optimisation involved the usage of 'B3LYP' method and '3-21G' basis set, a more basic basis set. A better basis set will be used later in the week.
test molecule |
Optimising BH3 molecule (3-21G basis set)
LOG FILE LINK: Media:Cma209 BH3 OPTIMISATION.LOG
Optimised B-H bond distance = 1.19 Å
Optimised H-B-H bond angle = 120.0o
Gaussian Calculation Summary
| BH3 Optimisation 3-21G | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Final energy in atomic units (au) | -26.46226338 |
| Gradient | 0.00020672 au |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Calculation Time Taken | 4 min 56 sec |
Logbook - "Item" table
Item Value Threshold Converged?
Maximum Force 0.000413 0.000450 YES
RMS Force 0.000271 0.000300 YES
Maximum Displacement 0.001610 0.001800 YES
RMS Displacement 0.001054 0.001200 YES
Predicted change in Energy=-1.071764D-06
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1935 -DE/DX = 0.0004 !
! R2 R(1,3) 1.1935 -DE/DX = 0.0004 !
! R3 R(1,4) 1.1935 -DE/DX = 0.0004 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Convergence has been achieved
Analysing the Optimised BH3 molecule (6-31G(d,p) basis set)
This optimisation involved the usage of 'B3LYP' method and '6-31G(d,p)' basis set, a better basis set. A better basis can optimise BH3 molecule with more accuracy, but the run takes slightly longer.
LOG FILE LINK: Media:CMA209 BH3 OPTIMISATION 631GDP.LOG
Optimised B-H bond distance = 1.19 Å
Optimised H-B-H bond angle = 120.0o
Gaussian Calculation Summary
| BH3 Optimisation 6-31G(d,p) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -26.61532363 |
| Gradient | 0.00000235 au |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Calculation Time Taken | 2 min 50 sec |
Logbook - "Item" table
Item Value Threshold Converged?
Maximum Force 0.000005 0.000450 YES
RMS Force 0.000003 0.000300 YES
Maximum Displacement 0.000019 0.001800 YES
RMS Displacement 0.000012 0.001200 YES
Predicted change in Energy=-1.304899D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1923 -DE/DX = 0.0 !
! R2 R(1,3) 1.1923 -DE/DX = 0.0 !
! R3 R(1,4) 1.1923 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Convergence has been achieved.
Energies of optimised BH3
For 3-21G optimised structure, total energy = -26.4622 au (4 d p)
For 6-31G(d,p) optimised structure, total energy = -26.6153 au (4 d p)
Energy Difference = 0.1531 au (4 d p) = 400 kJmol-1 (corrected to nearest 10 kJmol-1)
From the 2 different optimisations, we notice a drop in total energy from 3-21G optimised structure to 6-31G(d,p) optimised structure. This can be explained by the fact that the more accurately optimised structure allowed the observation the BH3 in a more stable state. Bond length of the 6-31G(d,p) optimised structure is also observed to be slightly lower than that of 3-21G optimised structure. The energy difference of both optimisations is ~400 kJmol-1, a rather significant diference considering it is similar to the bond length of a C-H bond.
TlBr3 / BBr3 Optimisation & Bond lengths comparison (Day 2)
Analysing the Optimised TlBr3 molecule (LanL2DZ basis set)
The optimisation of TlBr3 made use of pseudo-potentials and a larger basis set. Therefore, HPC is used in the optimisation calculation instead of Gaussian.
Optimised Tl-Br bond distance = 2.65 Å
Optimised Br-Tl-Br bond angle = 120.0o
Link to D-space
Link: DOI:10042/22521
Gaussian Calculation Summary
| TlBr3 Optimisation (Lanl2dz) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Final energy in atomic units (au) | -91.21812851 |
| Gradient | 0.00000090 au |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Calculation Time Taken | 0 min 38.1 sec |
Logbook - "Item" table
Item Value Threshold Converged?
Maximum Force 0.000002 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000014 0.001200 YES
Predicted change in Energy=-6.084112D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.651 -DE/DX = 0.0 !
! R2 R(1,3) 2.651 -DE/DX = 0.0 !
! R3 R(1,4) 2.651 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Convergence has been achieved
Comparison with Literature (Tl-Br Bond Distance)
Literature Tl-Br Bond Distance: 2.51 Å [1]
- ↑ 10.3891/acta.chem.scand.36a-0125
Analysing the Optimised BBr3 molecule (GEN basis set)
Optimised B-Br bond distance = 1.93 Å
Optimised Br-B-Br bond angle = 120.0o
Link to D-space
Link: DOI:10042/22522
Gaussian Calculation Summary
| BBr3 Optimisation (Gen Basis set) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | Gen |
| Final energy in atomic units (au) | -64.43645296 |
| Gradient | 0.00000382 au |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Calculation Time Taken | 0 min 33.8 sec |
Logbook - "Item" table
Item Value Threshold Converged?
Maximum Force 0.000008 0.000450 YES
RMS Force 0.000005 0.000300 YES
Maximum Displacement 0.000036 0.001800 YES
RMS Displacement 0.000023 0.001200 YES
Predicted change in Energy=-4.027600D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.934 -DE/DX = 0.0 !
! R2 R(1,3) 1.934 -DE/DX = 0.0 !
! R3 R(1,4) 1.934 -DE/DX = 0.0 !
! A1 A(2,1,3) 120.0 -DE/DX = 0.0 !
! A2 A(2,1,4) 120.0 -DE/DX = 0.0 !
! A3 A(3,1,4) 120.0 -DE/DX = 0.0 !
! D1 D(2,1,4,3) 180.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Convergernce has been achieved
Table of Bond Lengths
| BH3 | TlBr3 | BBr3 | |
| Bond Lengths / Å | 1.1923 | 2.6510 | 1.9340 |
Bond Angles for all 3 molecules are equal at 120o.
Discussion points
In the 3 molecules used for comparison, changing the ligand from H to Br increases the bond length as the Br is a much larger atom and is more diffuse compared to H. However, besides the bond length, bond angle remains unchanged as the geometry of all three compounds are the same (Trigonal planar). This is because H & Br are similar in terms of their bonding to the central atom as both contribute a single electron into formation of a single sigma bond. The preservation of trigonal planar geometry could only occur if the central elements are of valency of +3. Therefore, while changing the central element from B to Tl increases the bond length of the molecule, it did not change the bond angle as they are both in the same group in the periodic table. Alternatively, changing the central element to another one not in the same group will cause a change in both bond length and bond angle as the geometry of the molecule will be altered (ref NH3 tetrahedral geometry). Also, changing the ligand to one which is not a sigma donor would also alter the structure of the molecule as it may be capable of different kinds of bonding such as Tl d --> pi* backbonding.
In Gaussview, a bond is representative of the attractive interaction between 2 or more atoms. Bond strengths are determined by factors such as extent of nuclei-nuclei and extent of attractive forces between oppositely charged ions. An attractive interaction can only be considered a bond if it is deemed as significant enough in Gaussview. When interaction is too low, it will not show up as a bond in Gaussview.
Frequency analysis: Day 3
Frequency analysis for BH3
Link: Media:CMA209 BH3 FRQUENCY 1.LOG
Low frequencies --- -0.9034 -0.7346 -0.0054 6.7355 12.2480 12.2812 Low frequencies --- 1163.0003 1213.1853 1213.1880
Gaussian Calculation Summary
| BH3 Frequency (Gen Basis set) | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -26.61532363 |
| Gradient | 0.00000237 au |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Calculation Time Taken | 0 min 4.0 sec |
Table of Molecular Vibrations
| No. | Form of Vibration | Frequency | Intensity | Symmetry (D3H) |
| 1 | .png) Wagging: B atom moves in and out of the plane of the molecule.
|
1163.00 | 92.5478 | A2" |
| 2 | .png) Symmetrical Stretching: 2 of the H atoms scissoring about B in the plane.
|
1213.19 | 14.0553 | E' |
| 3 | .png) Rocking: 2 H atoms moves anticlockwise, while the other H atom moves clockwise.
|
1213.19 | 14.0589 | E' |
| 4 | .png) Symmetric Stretching: All 3 H atoms 'breathing' as they move inwards and outward in sync in the same plane
|
2582.26 | 0.0000 | A1' |
| 5 | .png) Asymmetrical Stretching: 2 H atoms stretches and contracts while the other remains stationary.
|
2715.43 | 126.3307 | E' |
| 6 | .png) Symmetrical Stretching: 2 H atoms strech in one direction while the other stretches in the opposite direction.
|
2715.43 | 126.3211 | E' |
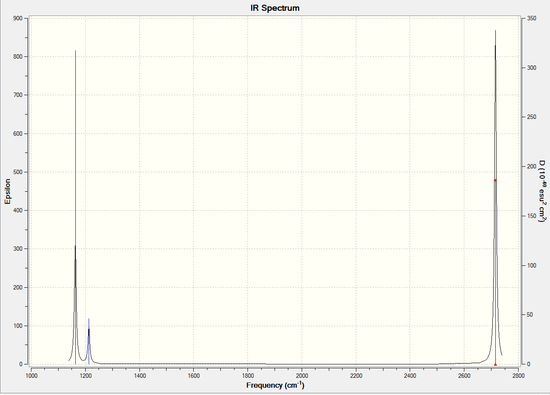
IR Spectrum of BH3
The missing peaks are due to some vibrations being very close in energies (Scissoring and rocking frequencies). Thus they show up as a single peak in the IR Spectrum. Also, for a vibrational mode in a molecule to be "IR active," it must be associated with changes in the dipole. A permanent dipole is not necessary, as the rule requires only a change in dipole moment.However, with symmetric stretching at 2582.26 cm-1, no change in dipole moment will be observed as the 3 H atoms move in the same direction thus are symmetric and IR-inactive.
Frequency analysis for TlBr3
Low frequencies --- -3.4213 -0.0026 -0.0004 0.0015 3.9367 3.9367 Low frequencies --- 46.4289 46.4292 52.1449
Link to D-space
Link: DOI:10042/22557
Gaussian Calculation Summary
| TlBr3 Frequency | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Final energy in atomic units (au) | -91.21812851 |
| Gradient | 0.00000088 au |
| Dipole Moment | 0.0000 Debye |
| Point Group | D3H |
| Calculation Time Taken | 0 min 28.1 sec |
IR Spectrum of TlBr3
Comparing the vibrational frequencies of BH3 and TlBr3
| BH3 Vibrational Frequency / kJmol-1 | TlBr3 Vibrational Frequency / kJmol-1 |
|---|---|
| 1213.19, 1213.19 (E') | 46.43, 46.43 (E') |
| 1163.00 (A2") | 52.14 (A2") |
| 2582.26 (A1') | 165.27 (A1') |
| 2715.43, 2715.43 (E') | 210.69, 210.69 (E') |
Comparison of IR spectra
The IR spectra shapes for both BH3 and TlBr3 are quite similar, indicative similar molecular structure, having similar vibrational modes. The value of frequencies of BH3 and TlBr3 are however quite different as B and H atoms are much lighter than Tl and Br atoms. Therefore, less energy is required for B and H to vibrate. Thus they are able to vibrate much more and much faster than Tl and Br. As such, higher frequencies of vibration will naturally be observed for BH3 as compared to TlBr3.
Reordering of modes could be observed. A2" is the lowest frequency vibration in BH3 but E' is the lowest frequency vibration in TlBr3, while A2" is swapped to the 2nd lowest frequency vibration above it. Reordering occurs as the effect on individual atoms in each vibration mode is different. Some atoms are stationary in certain vibrational modes, while others are in motion, and as such, change in mass of that atom will alter the overall vibrational frequency to different extents.
For both spectra two modes lie fairly closely together, the A2 and E' modes and then the other two modes also lie fairly close together, the A1' and E' modes, but higher in energy. This is because A2 and E' modes are bending frequencies while A1' and E' modes are stretching frequencies which are generally much higher in frequencies compared to bending ones.
Discussion
Using different methods and basis sets would give rise to different levels of accuracies measured. As shown in earlier analysis of BH3 optimisation, difference in energy could be as great as 400 kJ/mol, almost equivalent to the bond strength of a C-H bond. This makes the analysis and comparisons rather meaningless due to the inaccuracy. Hence it is crucial that all analysis are made based on the same method and basis sets used.
A frequency analysis allows us to make sure that the optimisation was done correctly. A correct optimisation has to be either a highest point/peak (transition state) or a lowest point/trough (ground state). This is carried out by taking the first and second derivatives of the optimisation. At any stationary point, the first derivative should be close to 0.
The frequency analysis test the second derivative. If all second derivative are positive, a minima(ground state) is obtained. If one negative value is obtained, then a maxima(transition state) is obtained. If more than 1 negative value is obtained, the optimisation is not successful.
Low frequencies represent the deviation from 0 based on the basis set used. The better the basis set, the closer the low frequencies values will be observed for each of the vibrational state.
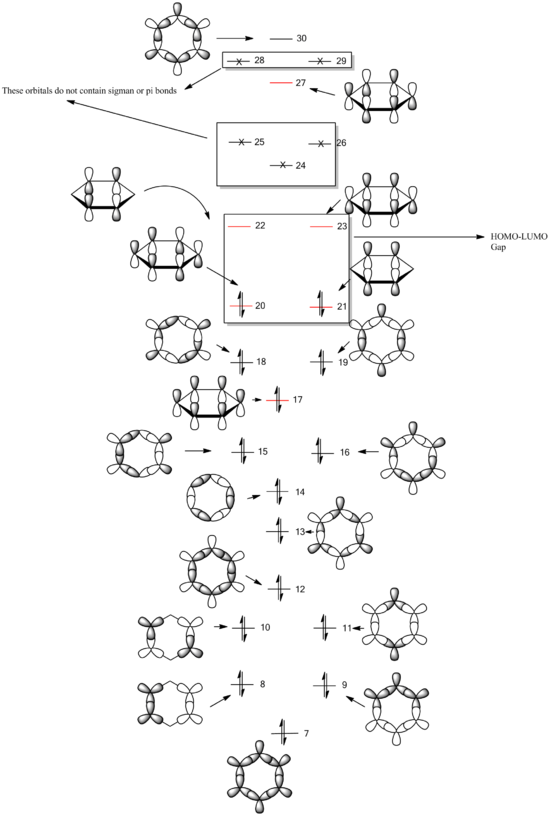
MO Diagram of BH3
There are no significant differences between real and LCAO MOs. Nevertheless, real MOs present a more general view of electronic distribution in the entire molecule, together with clear notification regarding location the nodal planes, while LCAO MOs can give us a more atoms-focussed picture of its bonding and anti-bonding nature in different orbital states.
Therefore, the qualitative MO theory using LCAO MOs are quite useful and accurate. However, as the molecule gets more complex, real MOs will be able to provide a better representation.
NH3(Day 4)
Analysing the Optimised NH3 molecule (6-31G(d,p) basis set)
Link: Media:NH3 OPTIMISATION 631GDP.LOG
Gaussian Calculation Summary
| NH3 Optimisation (6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -56.55776854 |
| Gradient | 0.00003886 au |
| Dipole Moment | 1.8463 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 10.0 sec |
Logbook - "Item" table
Item Value Threshold Converged?
Maximum Force 0.000200 0.000450 YES
RMS Force 0.000124 0.000300 YES
Maximum Displacement 0.000386 0.001800 YES
RMS Displacement 0.000261 0.001200 YES
Predicted change in Energy=-1.088496D-07
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.0007 -DE/DX = 0.0002 !
! R2 R(1,3) 1.0007 -DE/DX = 0.0002 !
! R3 R(1,4) 1.0007 -DE/DX = 0.0002 !
! A1 A(2,1,3) 107.5868 -DE/DX = 0.0 !
! A2 A(2,1,4) 107.5676 -DE/DX = 0.0 !
! A3 A(3,1,4) 107.5676 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -115.6371 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Convergence has been achieved
Analysing the Frequency NH3 molecule (6-31G(d,p) basis set)
Link: Media:NH3 FREQ.LOG
Low frequencies --- -9.4755 -0.0018 -0.0016 0.0011 33.0385 39.6310 Low frequencies --- 1089.7822 1694.1610 1694.3194
Gaussian Calculation Summary
| NH3 Frequency (6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -56.55776854 |
| Gradient | 0.00003881 au |
| Dipole Moment | 1.8463 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 8.0 sec |
Analysing the Energies NH3 molecule (6-31G(d,p) basis set)
Link: Media:NH3 ENERGY.LOG
Gaussian Calculation Summary
| NH3 Energy (6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -56.55776854 |
| Dipole Moment | 1.8463 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 2.0 sec |
NBO analysis of NH3
Charge Distribution
Charge Limits: -1.0 to 1.0
Specific NBO Charge for Nitrogen: -1.125
Specific NBO Charge for Hydrogen: 0.375
Optimisation of NH3BH3
Link: Media:BH3NH3 OPTIMISATION.LOG
Gaussian Calculation Summary
| NH3BH3 Optimisation (6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -83.22469032 |
| RMS Gradient Norm | 0.00005936 |
| Dipole Moment | 5.5648 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 47.0 sec |
Logbook - "Item" table
Item Value Threshold Converged?
Maximum Force 0.000121 0.000450 YES
RMS Force 0.000057 0.000300 YES
Maximum Displacement 0.000508 0.001800 YES
RMS Displacement 0.000294 0.001200 YES
Predicted change in Energy=-1.612062D-07
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,7) 1.21 -DE/DX = -0.0001 !
! R2 R(2,7) 1.21 -DE/DX = -0.0001 !
! R3 R(3,7) 1.21 -DE/DX = -0.0001 !
! R4 R(4,8) 1.0186 -DE/DX = -0.0001 !
! R5 R(5,8) 1.0186 -DE/DX = -0.0001 !
! R6 R(6,8) 1.0186 -DE/DX = -0.0001 !
! R7 R(7,8) 1.6681 -DE/DX = -0.0001 !
! A1 A(1,7,2) 113.8797 -DE/DX = 0.0 !
! A2 A(1,7,3) 113.8797 -DE/DX = 0.0 !
! A3 A(1,7,8) 104.5977 -DE/DX = 0.0 !
! A4 A(2,7,3) 113.8726 -DE/DX = 0.0 !
! A5 A(2,7,8) 104.5908 -DE/DX = 0.0 !
! A6 A(3,7,8) 104.5908 -DE/DX = 0.0 !
! A7 A(4,8,5) 107.8729 -DE/DX = 0.0 !
! A8 A(4,8,6) 107.8729 -DE/DX = 0.0 !
! A9 A(4,8,7) 111.0204 -DE/DX = 0.0 !
! A10 A(5,8,6) 107.8692 -DE/DX = 0.0 !
! A11 A(5,8,7) 111.0303 -DE/DX = 0.0 !
! A12 A(6,8,7) 111.0303 -DE/DX = 0.0 !
! D1 D(1,7,8,4) 179.9998 -DE/DX = 0.0 !
! D2 D(1,7,8,5) -60.0008 -DE/DX = 0.0 !
! D3 D(1,7,8,6) 60.0004 -DE/DX = 0.0 !
! D4 D(2,7,8,4) -59.9965 -DE/DX = 0.0 !
! D5 D(2,7,8,5) 60.0029 -DE/DX = 0.0 !
! D6 D(2,7,8,6) -179.9958 -DE/DX = 0.0 !
! D7 D(3,7,8,4) 59.9961 -DE/DX = 0.0 !
! D8 D(3,7,8,5) 179.9955 -DE/DX = 0.0 !
! D9 D(3,7,8,6) -60.0032 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Convergence has been achieved
Frequency analysis of NH3BH3
Link: Media:BH3NH3 FREQ.LOG
Low frequencies --- -0.0010 -0.0008 0.0008 18.5298 23.7970 41.0509 Low frequencies --- 266.2912 632.2325 639.8330
Gaussian Calculation Summary
| NH3BH3 Frequency (6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -83.22469032 |
| RMS Gradient Norm | 0.00005949 |
| Dipole Moment | 5.5648 Debye |
| Point Group | C1 |
| Calculation Time Taken | 0 min 38.0 sec |
Associative Energies Calculation
E(NH3)= -56.55776854 au
E(BH3)= -26.61532363 au
E(NH3BH3)= -83.22469032 au
ΔE
=E(NH3BH3)-[E(NH3)+E(BH3)]
=-83.22469032 + 56.55776854 + 26.61532363
=-0.05159815 au
=-135.47 kJmol-1
Week 2 Project: Aromaticity
Benzene
Optimisation of Benzene: Reference molecule
Link: DOI:10042/22851
Gaussian Calculation Summary
| Benzene Optimisation (6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -232.25821186 |
| RMS Gradient Norm | 0.00009338 |
| Dipole Moment | 0.0001 Debye |
| Point Group | C1 |
| Calculation Time Taken | 2 min 1.1 sec |
Logbook - "Item" table
Item Value Threshold Converged?
Maximum Force 0.000204 0.000450 YES
RMS Force 0.000084 0.000300 YES
Maximum Displacement 0.000870 0.001800 YES
RMS Displacement 0.000313 0.001200 YES
Predicted change in Energy=-4.983462D-07
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.3963 -DE/DX = 0.0001 !
! R2 R(1,6) 1.3961 -DE/DX = 0.0002 !
! R3 R(1,7) 1.0861 -DE/DX = 0.0002 !
! R4 R(2,3) 1.3961 -DE/DX = 0.0002 !
! R5 R(2,8) 1.0861 -DE/DX = 0.0002 !
! R6 R(3,4) 1.3963 -DE/DX = 0.0001 !
! R7 R(3,9) 1.0861 -DE/DX = 0.0002 !
! R8 R(4,5) 1.3961 -DE/DX = 0.0002 !
! R9 R(4,10) 1.0861 -DE/DX = 0.0002 !
! R10 R(5,6) 1.3963 -DE/DX = 0.0001 !
! R11 R(5,11) 1.0861 -DE/DX = 0.0002 !
! R12 R(6,12) 1.0861 -DE/DX = 0.0002 !
! A1 A(2,1,6) 119.9996 -DE/DX = 0.0 !
! A2 A(2,1,7) 119.9968 -DE/DX = 0.0 !
! A3 A(6,1,7) 120.0036 -DE/DX = 0.0 !
! A4 A(1,2,3) 120.0036 -DE/DX = 0.0 !
! A5 A(1,2,8) 119.9916 -DE/DX = 0.0 !
! A6 A(3,2,8) 120.0048 -DE/DX = 0.0 !
! A7 A(2,3,4) 119.9967 -DE/DX = 0.0 !
! A8 A(2,3,9) 120.0101 -DE/DX = 0.0 !
! A9 A(4,3,9) 119.9932 -DE/DX = 0.0 !
! A10 A(3,4,5) 119.9996 -DE/DX = 0.0 !
! A11 A(3,4,10) 119.9891 -DE/DX = 0.0 !
! A12 A(5,4,10) 120.0113 -DE/DX = 0.0 !
! A13 A(4,5,6) 120.004 -DE/DX = 0.0 !
! A14 A(4,5,11) 120.0048 -DE/DX = 0.0 !
! A15 A(6,5,11) 119.9912 -DE/DX = 0.0 !
! A16 A(1,6,5) 119.9965 -DE/DX = 0.0 !
! A17 A(1,6,12) 120.0072 -DE/DX = 0.0 !
! A18 A(5,6,12) 119.9963 -DE/DX = 0.0 !
! D1 D(6,1,2,3) -0.0059 -DE/DX = 0.0 !
! D2 D(6,1,2,8) 180.0021 -DE/DX = 0.0 !
! D3 D(7,1,2,3) -180.0099 -DE/DX = 0.0 !
! D4 D(7,1,2,8) -0.0019 -DE/DX = 0.0 !
! D5 D(2,1,6,5) -0.0055 -DE/DX = 0.0 !
! D6 D(2,1,6,12) -179.9972 -DE/DX = 0.0 !
! D7 D(7,1,6,5) -180.0016 -DE/DX = 0.0 !
! D8 D(7,1,6,12) 0.0068 -DE/DX = 0.0 !
! D9 D(1,2,3,4) 0.0119 -DE/DX = 0.0 !
! D10 D(1,2,3,9) 180.0087 -DE/DX = 0.0 !
! D11 D(8,2,3,4) 180.0039 -DE/DX = 0.0 !
! D12 D(8,2,3,9) 0.0007 -DE/DX = 0.0 !
! D13 D(2,3,4,5) -0.0064 -DE/DX = 0.0 !
! D14 D(2,3,4,10) -180.0058 -DE/DX = 0.0 !
! D15 D(9,3,4,5) 179.9968 -DE/DX = 0.0 !
! D16 D(9,3,4,10) -0.0026 -DE/DX = 0.0 !
! D17 D(3,4,5,6) -0.005 -DE/DX = 0.0 !
! D18 D(3,4,5,11) 180.0061 -DE/DX = 0.0 !
! D19 D(10,4,5,6) -180.0057 -DE/DX = 0.0 !
! D20 D(10,4,5,11) 0.0055 -DE/DX = 0.0 !
! D21 D(4,5,6,1) 0.011 -DE/DX = 0.0 !
! D22 D(4,5,6,12) 180.0027 -DE/DX = 0.0 !
! D23 D(11,5,6,1) 179.9999 -DE/DX = 0.0 !
! D24 D(11,5,6,12) -0.0085 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Convergence has been observed.
Frequency Analysis of Benzene: Reference molecule
Link: DOI:10042/22854
Gaussian Calculation Summary
| Benzene Optimisation (6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -232.25821186 |
| RMS Gradient Norm | 0.00009342 |
| Dipole Moment | 0.0001 Debye |
| Point Group | C1 |
| Calculation Time Taken | 5 min 31.7 sec |
Low frequencies --- -14.2203 -2.7103 -0.0006 -0.0004 0.0004 10.0048 Low frequencies --- 413.7277 414.5531 621.0442
Energy Analysis of Benzene: Reference molecule
Link: DOI:10042/22860
| Benzene Energy Analysis(6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -232.30851149 |
| Dipole Moment | 0.0001 Debye |
| Point Group | C1 |
| Calculation Time Taken | 1 min 34.2 sec |
Pyridinium
Optimisation of Pyridinium
Link: DOI:10042/22870
Gaussian Calculation Summary
| Pyridinium Optimisation(6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -248.66807395 |
| Gradient (au) | 0.00003913 |
| Dipole Moment | 10.7545 Debye |
| Point Group | C1 |
| Calculation Time Taken | 4 min 0.6 sec |
Logbook - "Item" table
Item Value Threshold Converged?
Maximum Force 0.000064 0.000450 YES
RMS Force 0.000023 0.000300 YES
Maximum Displacement 0.000702 0.001800 YES
RMS Displacement 0.000176 0.001200 YES
Predicted change in Energy=-6.968238D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.3839 -DE/DX = 0.0 !
! R2 R(1,5) 1.3988 -DE/DX = 0.0 !
! R3 R(1,6) 1.0835 -DE/DX = 0.0 !
! R4 R(2,7) 1.0832 -DE/DX = 0.0 !
! R5 R(2,12) 1.3523 -DE/DX = 0.0001 !
! R6 R(3,4) 1.3838 -DE/DX = 0.0 !
! R7 R(3,9) 1.0832 -DE/DX = 0.0 !
! R8 R(3,12) 1.3524 -DE/DX = 0.0 !
! R9 R(4,5) 1.3988 -DE/DX = 0.0 !
! R10 R(4,10) 1.0835 -DE/DX = 0.0 !
! R11 R(5,11) 1.0852 -DE/DX = 0.0 !
! R12 R(8,12) 1.0169 -DE/DX = 0.0 !
! A1 A(2,1,5) 119.082 -DE/DX = 0.0 !
! A2 A(2,1,6) 119.4192 -DE/DX = 0.0001 !
! A3 A(5,1,6) 121.4987 -DE/DX = -0.0001 !
! A4 A(1,2,7) 123.9294 -DE/DX = 0.0 !
! A5 A(1,2,12) 119.2362 -DE/DX = 0.0 !
! A6 A(7,2,12) 116.8344 -DE/DX = 0.0 !
! A7 A(4,3,9) 123.9326 -DE/DX = 0.0 !
! A8 A(4,3,12) 119.2355 -DE/DX = 0.0 !
! A9 A(9,3,12) 116.832 -DE/DX = 0.0 !
! A10 A(3,4,5) 119.0826 -DE/DX = 0.0 !
! A11 A(3,4,10) 119.4215 -DE/DX = 0.0 !
! A12 A(5,4,10) 121.4958 -DE/DX = -0.0001 !
! A13 A(1,5,4) 120.0549 -DE/DX = 0.0 !
! A14 A(1,5,11) 119.974 -DE/DX = 0.0 !
! A15 A(4,5,11) 119.9711 -DE/DX = 0.0 !
! A16 A(2,12,3) 123.3087 -DE/DX = 0.0 !
! A17 A(2,12,8) 118.3464 -DE/DX = 0.0 !
! A18 A(3,12,8) 118.3448 -DE/DX = 0.0 !
! D1 D(5,1,2,7) -180.0014 -DE/DX = 0.0 !
! D2 D(5,1,2,12) 0.0031 -DE/DX = 0.0 !
! D3 D(6,1,2,7) -0.0012 -DE/DX = 0.0 !
! D4 D(6,1,2,12) 180.0032 -DE/DX = 0.0 !
! D5 D(2,1,5,4) -0.0003 -DE/DX = 0.0 !
! D6 D(2,1,5,11) -180.0014 -DE/DX = 0.0 !
! D7 D(6,1,5,4) -180.0005 -DE/DX = 0.0 !
! D8 D(6,1,5,11) -0.0015 -DE/DX = 0.0 !
! D9 D(1,2,12,3) -0.0045 -DE/DX = 0.0 !
! D10 D(1,2,12,8) -180.0031 -DE/DX = 0.0 !
! D11 D(7,2,12,3) -180.0003 -DE/DX = 0.0 !
! D12 D(7,2,12,8) 0.001 -DE/DX = 0.0 !
! D13 D(9,3,4,5) 180.0008 -DE/DX = 0.0 !
! D14 D(9,3,4,10) -0.0003 -DE/DX = 0.0 !
! D15 D(12,3,4,5) 0.0 -DE/DX = 0.0 !
! D16 D(12,3,4,10) -180.001 -DE/DX = 0.0 !
! D17 D(4,3,12,2) 0.0029 -DE/DX = 0.0 !
! D18 D(4,3,12,8) 180.0015 -DE/DX = 0.0 !
! D19 D(9,3,12,2) 180.0022 -DE/DX = 0.0 !
! D20 D(9,3,12,8) 0.0009 -DE/DX = 0.0 !
! D21 D(3,4,5,1) -0.0012 -DE/DX = 0.0 !
! D22 D(3,4,5,11) -180.0002 -DE/DX = 0.0 !
! D23 D(10,4,5,1) 179.9999 -DE/DX = 0.0 !
! D24 D(10,4,5,11) 0.0009 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Frequency Analysis of Pyridinium
Link: DOI:10042/22868
Gaussian Calculation Summary
| Pyridinium Frequency(6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -248.66807395 |
| Gradient (au) | 0.00003898 |
| Dipole Moment | 10.7545 Debye |
| Point Group | C1 |
| Calculation Time Taken | 5 min 40.1 sec |
Low frequencies --- -7.2067 -0.0009 -0.0008 -0.0004 17.3442 18.5477 Low frequencies --- 392.4565 404.0619 620.4717
Energy analysis of Pyridinium
Link: DOI:10042/22871
Gaussian Calculation Summary
| Pyridinium Frequency(6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -248.66807395 |
| Dipole Moment | 10.7545 Debye |
| Point Group | C1 |
| Calculation Time Taken | 1 min 12.3 sec |
Boratabenzene
Boratabenzene Optimisation
Link: DOI:10042/22893
Gaussian Calculation Summary
| Boratabenzene(6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -219.02052559 |
| Gradient (au) | 0.00000465 |
| Dipole Moment | 4.7552 Debye |
| Point Group | C1 |
| Calculation Time Taken | 5 min 54.0 sec |
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000022 0.001800 YES
RMS Displacement 0.000006 0.001200 YES
Predicted change in Energy=-2.198796D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.3989 -DE/DX = 0.0 !
! R2 R(1,7) 1.0968 -DE/DX = 0.0 !
! R3 R(1,12) 1.514 -DE/DX = 0.0 !
! R4 R(2,3) 1.4052 -DE/DX = 0.0 !
! R5 R(2,8) 1.0969 -DE/DX = 0.0 !
! R6 R(3,4) 1.4052 -DE/DX = 0.0 !
! R7 R(3,9) 1.0915 -DE/DX = 0.0 !
! R8 R(4,5) 1.3988 -DE/DX = 0.0 !
! R9 R(4,10) 1.0969 -DE/DX = 0.0 !
! R10 R(5,11) 1.0968 -DE/DX = 0.0 !
! R11 R(5,12) 1.514 -DE/DX = 0.0 !
! R12 R(6,12) 1.2185 -DE/DX = 0.0 !
! A1 A(2,1,7) 116.0072 -DE/DX = 0.0 !
! A2 A(2,1,12) 120.0601 -DE/DX = 0.0 !
! A3 A(7,1,12) 123.9327 -DE/DX = 0.0 !
! A4 A(1,2,3) 122.1773 -DE/DX = 0.0 !
! A5 A(1,2,8) 120.3702 -DE/DX = 0.0 !
! A6 A(3,2,8) 117.4524 -DE/DX = 0.0 !
! A7 A(2,3,4) 120.4157 -DE/DX = 0.0 !
! A8 A(2,3,9) 119.7954 -DE/DX = 0.0 !
! A9 A(4,3,9) 119.7889 -DE/DX = 0.0 !
! A10 A(3,4,5) 122.1793 -DE/DX = 0.0 !
! A11 A(3,4,10) 117.4605 -DE/DX = 0.0 !
! A12 A(5,4,10) 120.3603 -DE/DX = 0.0 !
! A13 A(4,5,11) 116.0177 -DE/DX = 0.0 !
! A14 A(4,5,12) 120.0604 -DE/DX = 0.0 !
! A15 A(11,5,12) 123.9218 -DE/DX = 0.0 !
! A16 A(1,12,5) 115.1071 -DE/DX = 0.0 !
! A17 A(1,12,6) 122.4433 -DE/DX = 0.0 !
! A18 A(5,12,6) 122.4496 -DE/DX = 0.0 !
! D1 D(7,1,2,3) -179.9997 -DE/DX = 0.0 !
! D2 D(7,1,2,8) 0.0001 -DE/DX = 0.0 !
! D3 D(12,1,2,3) 0.0001 -DE/DX = 0.0 !
! D4 D(12,1,2,8) -180.0001 -DE/DX = 0.0 !
! D5 D(2,1,12,5) 0.0 -DE/DX = 0.0 !
! D6 D(2,1,12,6) 179.9998 -DE/DX = 0.0 !
! D7 D(7,1,12,5) 179.9997 -DE/DX = 0.0 !
! D8 D(7,1,12,6) -0.0005 -DE/DX = 0.0 !
! D9 D(1,2,3,4) -0.0002 -DE/DX = 0.0 !
! D10 D(1,2,3,9) -180.0 -DE/DX = 0.0 !
! D11 D(8,2,3,4) 180.0 -DE/DX = 0.0 !
! D12 D(8,2,3,9) 0.0002 -DE/DX = 0.0 !
! D13 D(2,3,4,5) 0.0002 -DE/DX = 0.0 !
! D14 D(2,3,4,10) -179.9997 -DE/DX = 0.0 !
! D15 D(9,3,4,5) 180.0 -DE/DX = 0.0 !
! D16 D(9,3,4,10) 0.0 -DE/DX = 0.0 !
! D17 D(3,4,5,11) -180.0002 -DE/DX = 0.0 !
! D18 D(3,4,5,12) -0.0001 -DE/DX = 0.0 !
! D19 D(10,4,5,11) -0.0003 -DE/DX = 0.0 !
! D20 D(10,4,5,12) 179.9998 -DE/DX = 0.0 !
! D21 D(4,5,12,1) 0.0 -DE/DX = 0.0 !
! D22 D(4,5,12,6) -179.9998 -DE/DX = 0.0 !
! D23 D(11,5,12,1) 180.0001 -DE/DX = 0.0 !
! D24 D(11,5,12,6) 0.0003 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Boratabenzene Frequency Analysis
Link: DOI:10042/22894
Gaussian Calculation Summary
| Boratabenzene(6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -219.02052559 |
| Gradient (au) | 0.00000471 |
| Dipole Moment | 4.7552 Debye |
| Point Group | C1 |
| Calculation Time Taken | 5 min 54.0 sec |
Low frequencies --- -14.2027 -0.0003 -0.0002 0.0003 9.1600 14.3420 Low frequencies --- 371.0584 404.5446 565.0798
Boratabenzene Energy Analysis
Link: DOI:10042/22898
Gaussian Calculation Summary
| Boratabenzene energy(6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -219.02052559 |
| Dipole Moment | 4.7552 Debye |
| Point Group | C1 |
| Calculation Time Taken | 1 min 10.3 sec |
Borazine
Borazine Optimisation
Link: DOI:10042/22899
Gaussian Calculation Summary
| Borazine Optimsation (6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -242.68459819 |
| Gradient (au) | 0.00006417 |
| Dipole Moment | 0.0003Debye |
| Point Group | C1 |
| Calculation Time Taken | 3 min 36.2 sec |
Logbook - "Item" table
Item Value Threshold Converged?
Maximum Force 0.000086 0.000450 YES
RMS Force 0.000033 0.000300 YES
Maximum Displacement 0.000252 0.001800 YES
RMS Displacement 0.000077 0.001200 YES
Predicted change in Energy=-9.332344D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,8) 1.1949 -DE/DX = 0.0001 !
! R2 R(2,11) 1.0097 -DE/DX = 0.0 !
! R3 R(3,9) 1.1949 -DE/DX = 0.0001 !
! R4 R(4,12) 1.0097 -DE/DX = 0.0 !
! R5 R(5,7) 1.1949 -DE/DX = 0.0001 !
! R6 R(6,10) 1.0097 -DE/DX = 0.0 !
! R7 R(7,10) 1.4307 -DE/DX = -0.0001 !
! R8 R(7,12) 1.4307 -DE/DX = -0.0001 !
! R9 R(8,10) 1.4306 -DE/DX = -0.0001 !
! R10 R(8,11) 1.4307 -DE/DX = -0.0001 !
! R11 R(9,11) 1.4307 -DE/DX = -0.0001 !
! R12 R(9,12) 1.4307 -DE/DX = -0.0001 !
! A1 A(5,7,10) 121.437 -DE/DX = 0.0 !
! A2 A(5,7,12) 121.4399 -DE/DX = 0.0 !
! A3 A(10,7,12) 117.123 -DE/DX = 0.0 !
! A4 A(1,8,10) 121.4407 -DE/DX = 0.0 !
! A5 A(1,8,11) 121.4364 -DE/DX = 0.0 !
! A6 A(10,8,11) 117.1229 -DE/DX = 0.0 !
! A7 A(3,9,11) 121.4415 -DE/DX = 0.0 !
! A8 A(3,9,12) 121.4374 -DE/DX = 0.0 !
! A9 A(11,9,12) 117.1211 -DE/DX = 0.0 !
! A10 A(6,10,7) 118.5602 -DE/DX = 0.0 !
! A11 A(6,10,8) 118.5628 -DE/DX = 0.0 !
! A12 A(7,10,8) 122.877 -DE/DX = 0.0 !
! A13 A(2,11,8) 118.5609 -DE/DX = 0.0 !
! A14 A(2,11,9) 118.561 -DE/DX = 0.0 !
! A15 A(8,11,9) 122.8781 -DE/DX = 0.0 !
! A16 A(4,12,7) 118.5641 -DE/DX = 0.0 !
! A17 A(4,12,9) 118.5579 -DE/DX = 0.0 !
! A18 A(7,12,9) 122.878 -DE/DX = 0.0 !
! D1 D(5,7,10,6) 0.0003 -DE/DX = 0.0 !
! D2 D(5,7,10,8) 179.997 -DE/DX = 0.0 !
! D3 D(12,7,10,6) -179.9999 -DE/DX = 0.0 !
! D4 D(12,7,10,8) -0.0032 -DE/DX = 0.0 !
! D5 D(5,7,12,4) 0.0036 -DE/DX = 0.0 !
! D6 D(5,7,12,9) -179.9997 -DE/DX = 0.0 !
! D7 D(10,7,12,4) -179.9962 -DE/DX = 0.0 !
! D8 D(10,7,12,9) 0.0005 -DE/DX = 0.0 !
! D9 D(1,8,10,6) -0.0025 -DE/DX = 0.0 !
! D10 D(1,8,10,7) -179.9992 -DE/DX = 0.0 !
! D11 D(11,8,10,6) 179.9975 -DE/DX = 0.0 !
! D12 D(11,8,10,7) 0.0008 -DE/DX = 0.0 !
! D13 D(1,8,11,2) -0.0057 -DE/DX = 0.0 !
! D14 D(1,8,11,9) -179.9955 -DE/DX = 0.0 !
! D15 D(10,8,11,2) 179.9944 -DE/DX = 0.0 !
! D16 D(10,8,11,9) 0.0045 -DE/DX = 0.0 !
! D17 D(3,9,11,2) 0.0035 -DE/DX = 0.0 !
! D18 D(3,9,11,8) 179.9933 -DE/DX = 0.0 !
! D19 D(12,9,11,2) -179.9968 -DE/DX = 0.0 !
! D20 D(12,9,11,8) -0.007 -DE/DX = 0.0 !
! D21 D(3,9,12,4) 0.0007 -DE/DX = 0.0 !
! D22 D(3,9,12,7) -179.996 -DE/DX = 0.0 !
! D23 D(11,9,12,4) -179.9989 -DE/DX = 0.0 !
! D24 D(11,9,12,7) 0.0044 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Borazine Frequency Analysis
Link: DOI:10042/22900
Gaussian Calculation Summary
| Borazine Frequency (6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -242.68459819 |
| Gradient (au) | 0.00006420 |
| Dipole Moment | 0.0003 Debye |
| Point Group | C1 |
| Calculation Time Taken | 5 min 32.6 sec |
Low frequencies --- -7.1011 0.0003 0.0009 0.0010 7.3491 13.0340 Low frequencies --- 288.5920 290.5613 404.2303
Borazine Energy Analysis
Link: DOI:10042/22901
Gaussian Calculation Summary
| Borazine Energy (6-31G(d,p)) | |
|---|---|
| File type | .log |
| Calculation Type | SP |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final energy in atomic units (au) | -242.68459819 |
| Dipole Moment | 0.0003 Debye |
| Point Group | C1 |
| Calculation Time Taken | 1 min 18.9 sec |
Analysis
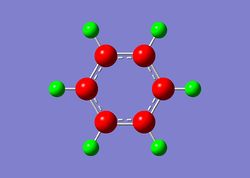
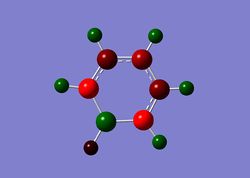
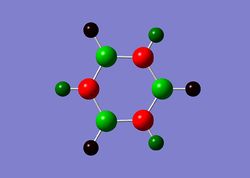
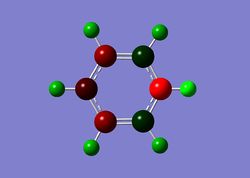
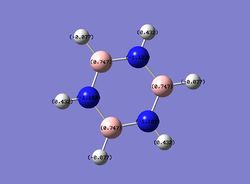
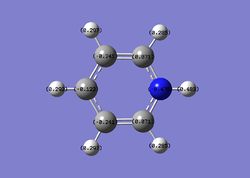
Charge Distribution
| Benzene | Boratabenzene | Borazine | Pyridinium |
|---|---|---|---|
|
|
|
|
|
|
|
|
The charge distribution of benzene is observed to be very even distribution. All the 6 carbon atoms in the ring possess the same charge number of -0.239. However, in boratabenzene and pyridinium, due to the hetero atom in the ring, the charges are not evenly distributed though aromaticity is preserved.
In the case of boratabenzene, the boron atom carries a positive charge (+0.202), while the neighbouring carbon atoms are more negatively charged compared to benzene. Carbon is more electronegative than boron, thus electron densities on boron is lower than on the carbon atoms. This difference in charge distribution would consequently affect the reactivity of the molecule. The proximity of the carbon atoms and boron also plays a part in the charge distribution as carbon atoms which are closer to boron has a more negative charge (-0.588) compared to carbons which are further away from boron (-0.250, -0.340).
On the other hand, in pyridinium, the negative charge is concentrated on the nitrogen (-0.476), as it is more electronegative. The carbons in the ring are all less negatively charged than benzene and the closer the carbons to nitrogen in proximity, the more positive it gets. For instance, the carbons adjacent to nitrogen has a charge of +0.071 compared to atoms further away from nitrogen (-0.241, -0.122).
Interestingly, the charge distribution on the meta positions of boratabenzene and pyridinium are least affected by the change in heteroatom. In benzene, the charge at all carbon positions are -0.239, while they are -0.250 and -0.241 in boratabenzene and pyridinium respectively. This is most probably due to the resonance effect of the heteroatom activating mostly only the ortho and para positions of the ring. Thus, reactivity in these heterocyclic rings are typically higher in the ortho and para positions, as compared to the meta positions.
In borazine, due to the alternating nitrogen and boron atoms, they have a very distinct charge distribution where all boron atoms carry a highly positive charge of +0.747, while nitrogens all carry the same negative charge of -1.102. Therefore, even though borazine is an aromatic compound, its alternating charge distribution pattern makes it more vulnerable to attack from nucleophiles (at B atoms) and electrophiles (at N atoms). In comparison, borazine is consequently much more reactive than benzene.
Molecular Orbitals of Benzene (sigma & pi orbitals only)
The red LCAO MO states the usual pi-orbitals that are always shown in textbooks. In aromatic systems, the electrons are delocalised and this can be observed from the real MO diagrams. MOs which are more stable are highly symmetrical and have less nodal plans so electrons could be easily spread out in the structure. This effect cannot be fully represented by LCAO representations as they show electrons in their localised states.
- Comparing Molecular Orbitals
| MO | Benzene | Boratabenzene | Borazine | Pyridinium |
|---|---|---|---|---|
| 7 (fully-sigma) | 
|
|
|
|
| 17 (pi) | 
|
|
|
|
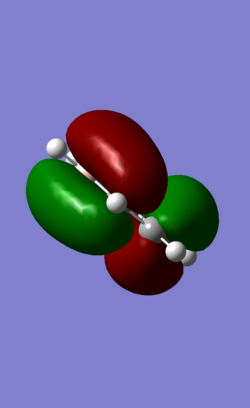
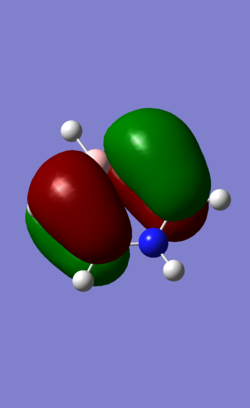
| 21 (HOMO) | 
|
|
|
|
MO 7 is a σ fully bonding orbital. Benzene shows a regular and symmetrical hexagonal shape, showing that the electron is distributed evenly among all C atoms. In pyridinium and boratabenzene, the shape was distorted slightly. In pyridinium, the MO shifted towards N atom and the MO shifted away from B atom. MO 7 for borazine follows the same trend with pyridinium and boratabenzene. Electrons are more likely to be found closer to N than to B given the higher electronegativity of N. Therefore, it formed a triangle shape, with the boron atom exposed, showing low electron density near boron. The MO comparisons very much agree with the analysis and comparison of charge distributions in the previous section.
MO 17 is a pi fully bonding orbital. The stability of aromatic compound is conferred by the delocalised pi orbitals electron cloud present. As with all pi orbitals, the top and bottom of the planar strucutre are of opposite phases. Similar to MO 7, when substituted, electron density shifts towards the more electronegative N atom and moves away from boron tyipcally. Pyridinium MO 17 is distorted slightly towards N while boratabenzene MO 17 is distorted slightly away from B. Borazine MO 17 also has a hexagonal shape but with 3 boron ends sticking out, showing high electron density present on the electronegative N atoms in the ring.
MO 21 is the HOMO of the molecule. it has 1 nodal planes dissecting the ring across two atoms across one another. This splits the orbitals into 2 sections of pi electrons in the opposite phase. In benzene, the 2 pi orbitals are the symmetrical and of the same size. In pyridinium, there is a slight distortion in the pi orbital shape as the neighbouring carbons to nitrogen have less electron density.. This distortion effect is not as pronounced as that in MO7/17 as the nitrogen atom (on the nodal plane) is not directly involved in formation of the MO. In boratabenzene, similarly, B atom is found on one of the nodal plane but exerts an influence on distorting electron density of neighbouring carbon atoms towards the Boron end. In Borazine MO 21, this secondary distortion effect is more pronounced as an obvious increase in electron density is observed from the nitrogen end to the boron end of the nodal plane.
Effect of Substitution
When carbon atoms are substituted by hetero atoms, the degenerate states observed in the LCAO MOs become non-degenerate and will increase or decrease depending on nature of hetero atom and which MO is influenced more by the hetero atom. A more symmetric molecule typically has more degenerate states compared to a less symmetric one and addition of hetero atom lowers the symmetry of the molecule.
The substitution also may result in the raising or lowering of energy levels of molecular orbitals that are formed from LCAOs. The atomic orbital of more electronegative atoms are usually lower than that of less electronegative atoms especially when comparing isoelectronic compounds.For instance, when carbon is substituted by nitrogen in pyridinium, due to increased electronegativity, the bonding orbitals will likely observe a decrease in energy levels due to a lower energy nitrogen AO. Correspondingly, the energy gaps between the MOs will become closer or further from one another due to the same reason.