Rep:Mod:CharlotteMadill
Introduction
A Potential Energy Surface (PES) describes the potential energy of a chemical system as a function of the location of the atoms in this system. In a chemical reaction, the system can be displaced from its equilibrium by any degree of freedom, such as translation or rotation. One or more of these degrees of freedom can be plotted against the potential energy; if only one coordinate is plotted, a one-dimensional Energy Profile is produced, however including more than one coordinate leads to an n-dimensional PES plot. Evaluating the stationary points, points on the PES where the gradient is zero, relate to physical information about the system; minima refer to chemically stable species, (i.e. reactants and products) and saddle points refer to transition states. These can be differentiated from each other by taking the second derivative at these points; reactants and products will have a positive curvature in all coordinates whereas transition states will have a negative curvature in only one coordinate. Using the Gaussian program, a transition state can also be identified by having one imaginary (negative) frequency in a frequency calculation, and a minimum will have no imaginary frequencies.
Nf710 (talk) 14:00, 4 November 2016 (UTC)Very good, if you had included something about the methods it would have been even better.
Exercise 1: Reaction of Butadiene with Ethylene

MO analysis
This is a typical Diels-Alder reaction and the reactants, transition state and product have been calculated and analysed with Gaussian at the PM6 level. The obtention of a transition state was confirmed by having one imaginary frequency of -949.04 in the frequency calculation of the TS.

The MO diagram above illustrates the HOMO and LUMO for the reactants and the transition state. Below are the corresponding MOs obtained from the calculations.
| Ethylene | Butadiene | Transition state | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
The calculated MOs correlate to the MO diagram therefore proving that the HOMO of ethylene interacts with the LUMO of butadiene as they are both of gerade symmetry and the HOMO of butadiene interacts with the LUMO of ethylene as they are both of ungerade symmetry. It can therefore be concluded that a reaction is only allowed when MOs of the same symmetry can interact; the orbital overlap integral is only non-zero if both orbitals have the same symmetry, i.e both gerade or ungerade. This is a standard Diels-Alder reaction as the HOMO of the dienophile, ethylene, is of lower energy than the HOMO of the diene, butadiene.
Nf710 (talk) 14:13, 4 November 2016 (UTC) Correct understanding of the symetry. Your TS orbitals dont look optimised, and I looked in your Jmol and you had it on the wrong frame, you want frame 6 as this is the output with the MOs. Dont worry no marks lost your log file is good.
Bond length analysis
| Bonded carbon atoms | Bond Length (Å) | ||
|---|---|---|---|
| Reactants | Transition State | Product | |
| C1&C2 | 1.33339 | 1.37978 | 1.50034 |
| C2&C3 | 1.47086 | 1.41115 | 1.33766 |
| C3&C4 | 1.33334 | 1.37976 | 1.50034 |
| C4&C5 | n/a | 2.11466 | 1.54003 |
| C5&C6 | 1.32731 | 1.38174 | 1.54003 |
| C6&C1 | n/a | 2.11465 | 1.54003 |
Going from products to reactants, C1, C4, C5 and C6 go from being sp2 hybridised to sp3 hybridised or in other words, double bonds between C1&C2, C3&C4 and C5&C6 become single bonds. This is demonstrated by the gradual lengthening of these bonds as seen in the table above. C2 and C3 remain sp2 hybridised and the bond between them transforms from a single to a double bond, corresponding to the shortening of the bond length evident in the table. The literature values for relevant bond lengths are as follows; for a C-C bond between two sp2 hybridised carbons in a conjugated system such as butadiene: 1.46Å, for a C=C bond between two sp2 hybridised carbons: 1.32Å, for a C-C bond in cyclohexene: 1.54Å and for a C=C bond in cyclohexene: 1.33Å [1]. This shows a high degree of accuracy in the calculated bond lengths in the table. The van der Waals radius of a carbon atom is 1.7Å [2] and the partially formed bond lengths between C4&C5 and C6&C1 in the transition state are 2.11Å which is lower than twice the v.d.W radius meaning there is significant interaction between the atoms at this stage of the reaction.
IRC analysis
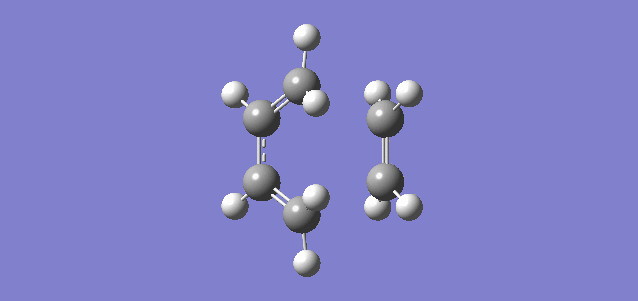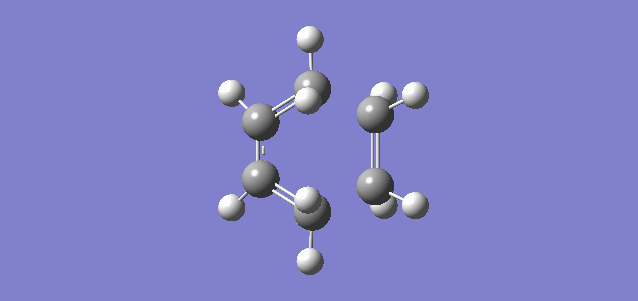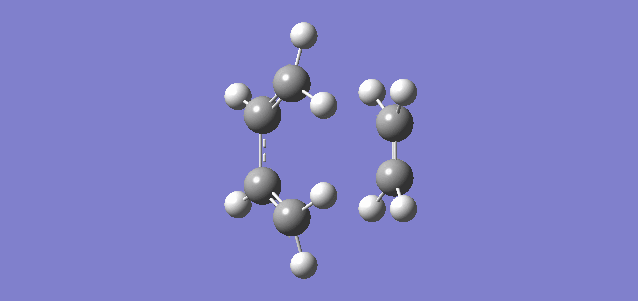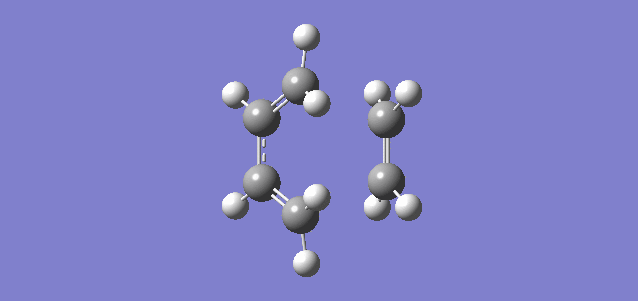
Shown above is the vibration referring to the reaction path, or in other words the imaginary frequency of the TS. It shows the terminal carbon atoms of both reactants moving towards each other and a compression of the C-C bond of the inner carbons of the butadiene, consistent with the transition from a single C-C bond to a double C=C bond. It can be seen that the new C-C bonds form synchronously which is consistent with there being no substituents and therefore no steric hinderance or electron donation or withdrawal on any of the carbon atoms. The vibration relating to the lowest positive frequency shows the molecules vibrating in a different degree of freedom and does not relate to the reaction path.
Media:IRC_BUTADIENE+ETHENE_PM6.LOG
Nf710 (talk) 14:27, 4 November 2016 (UTC) Good underdstanding
Exercise 2: Reaction of Benzoquinone and Cyclopentadiene
Reactants, transition states and products for both the endo- and exo- adducts were calculated at the B3LYP/6-31G(d) level and the obtention of a TS was confirmed by having one imaginary frequency present in the frequency calculations of the TS; -440.84 for the endo and -439.92 for the exo.
MO analysis
Calculations at the B3LYP/6-31G(d) level reveal that the HOMO of the dienophile, benzoquinone, is lower in energy than the HOMO of the diene, cyclopentadiene. This shows that the reaction is a standard Diels-Alder reaction and can be applied to the MO diagram drawn for Exercise 1. This is to be expected as benzoquinone contains electron withdrawing C=O substituents either side of the C=C double bond, resulting in an electron deficieint dienophile, and cyclopentadiene is an electron rich aromatic ring, resulting in an electron rich diene. The HOMO and LUMO for both endo- and exo- products are shown below. This shows that there are stronger secondary orbital interactions in the HOMO of the endo- transition state than in the exo- transition state, due to the fact that the pi system of cyclopentadiene can also interact with the C=C and C=O orbitals of the benzoquinone molecule which are not directly involved in the reaction. This extra interaction lowers the energy of the endo- transition state making it form faster and therefore it is the kinetic product, see below for further energy data.
(You should include symmetry labels for your MOs. The gerade orbitals are the HOMO-1 and LUMO+1 Tam10 (talk) 10:29, 31 October 2016 (UTC))
Nf710 (talk) 14:53, 4 November 2016 (UTC) Nice understanding of SSO
 |
 |
 |
 |
Thermochemistry analysis
| Reactants | TS | Product | Ea | ΔGr | |
|---|---|---|---|---|---|
| Endo | -575.431 | -575.381 | -575.432 | 0.005 | 0.001 |
| Exo | -575.431 | -575.384 | -575.427 | 0.047 | 0.004 |
The Gibbs Free Energy, activation energy and reaction energy are given above with all energies in Hartrees for both the endo and exo products. Using the MO theory above, I would expect the endo product to be the kinetic product and the exo product to be the thermodynamic product, which in terms of activation energy and reaction energy would mean that the endo product would have a lower Ea and smaller ΔGr . However my calculations indicate that the endo product is the thermodynamic product as it has a lower Gibbs free energy than the exo product and its Ea and ΔGr in comparison to the exo adduct are the opposite of what was expected. In fact, the exo product has been calculated to have a higher Gibbs Free Energy than the reactants meaning theoretically this reaction would not be spontaneous.
Nf710 (talk) 14:58, 4 November 2016 (UTC) Your TS energies are correct, but your reactant are slightly because you havwe take the two products at infinite separation however, Your product energy of endo is in correct and therefore you get the wrong conclusions about the thermo product. But your understanding that the endo is the kentic product is correct.
Exercise 3: Diels-Alder vs Cheletropic
Diels-Alder Exo Product

| IRC | Energy profile using energies from optimised reactants, TS and product |
|---|---|
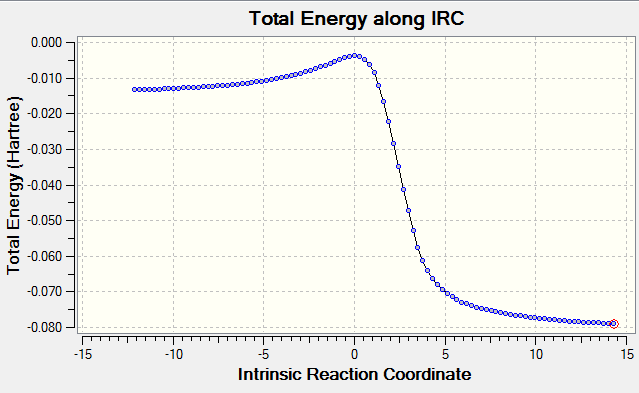
|

|
Diels-Alder Endo Product
| IRC | Energy profile using energies from optimised reactants, TS and product |
|---|---|
|

|
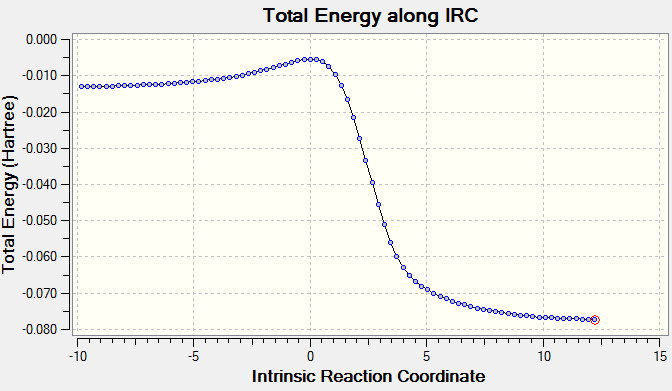
In both of the IRC animations it can be seen that around the time of the TS, there is a delocalisation of electrons throughout the molecule including in the 6-membered hydrocarbon ring due to the fact that xylelene is highly unstable. It can be seen from the Energy Profiles that the preferred route for the Diels-Alder reaction is to produce the endo product as it has a lower Ea and a larger ΔGr. This is comparable to Exercise 1 where secondary orbital interactions increase stability. In this case, the pi orbitals of the S=O bond in the endo product are able to interact with the pi orbitals of the benzene ring, which is not possible geometrically in the exo product.
(You should optimise the reactants together as this is the barrier the system has to overcome Tam10 (talk) 10:39, 31 October 2016 (UTC))
Cheletropic Product
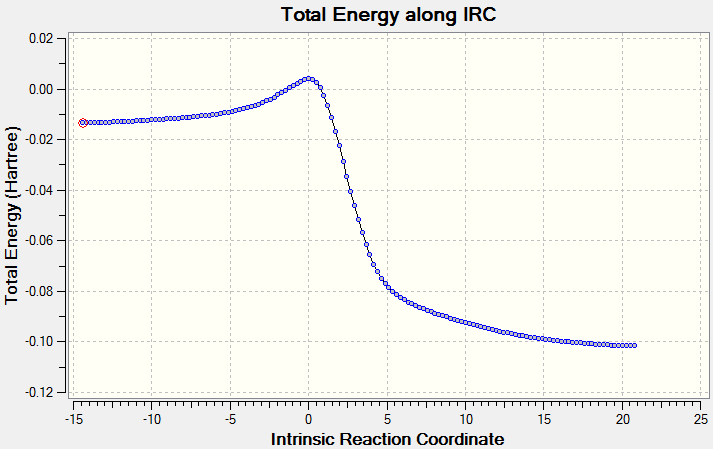
| IRC | Energy profile using energies from optimised reactants, TS and product |
|---|---|
|

|
Media:CHELETROPIC_TS_PM6.LOG
There is only one way for this reaction to occur as shown above. The cheletropic path has a higher activation energy but a much greater Gibbs Free Energy change than the Diels-Alder path. This indicates that it is the thermodynamic product and would therefore form under thermodynamic control whereas the Diels-Alder products would form if the reaction was under kinetic control. The higher activation energy and therefore transition state energy for the cheletropic reaction may be due to the formation of a 5-membered ring, which is more strained than a 6-membered ring as is seen in the Diels-Alder reaction.
Conclusion
In Exercise 1, MO analysis based on Gaussian calculations confirmed a proposed MO diagram for the formation of the transition state and demonstrated that the reaction is an example of a standard Diels-Alder reaction. An IRC calculation established that the bonds form synchronously due to the lack of substituents and therefore steric hinderance.
In Exercise 2, MO analysis confirmed the assumption that this reaction would also be a standard Diels-Alder reaction due to an electron deficient dienophile and an electron rich diene, and furthermore it demonstrated that there is substantial secondary orbital interaction in the transition state HOMO of the endo- adduct. This concluded that the endo product would be the major product of the reaction as long as it was conducted under kinetic control. However analysis of the Gibbs Free Energy suggested the endo-product was the thermodynamic product and that the exo- product would not form spontaneously at all, and therefore also supporting the idea that the endo- would be the major (if not only) product of the reaction, yet conflicting with the theory that the exo- product is the thermodynamic product, with the lowest Gibbs Free Energy. This discrepancy could come from not calculating on an accurate enough level despite B3LYP/6-31G(d) having been the method used.
In Exercise 3, a reaction with three possible products was investigated. An IRC concluded that in all three cases there is delocalisation of electrons into the aromatic ring of xylelene around the TS stage of the reaction due to its high level of instability. Gibbs Free Energy analysis suggested that the cheletropic pathway is thermodynamically favoured due to a high activation energy but very high change in Gibbs Free Energy and that the Diels-Alder pathway is kinetically favoured. Out of the two adducts the energy profiles suggest the endo product is the major product due to a smaller activation energy and larger reaction energy. This can be attributed to secondary orbital interactions not physically possible in the exo product.
Overall, the use of computational chemistry has helped to confirm a list of theories without having to do any chemical experiments and has shed valuable light on fleeting transition states which are almost impossible to analyse in physical life.
