Rep:Mod:Cfl082
Module 2: Charlene Lawton
Optimisation of BH3
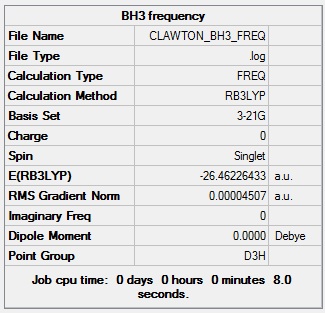
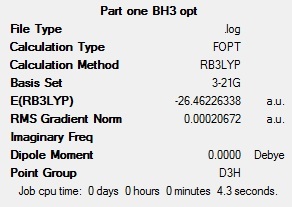
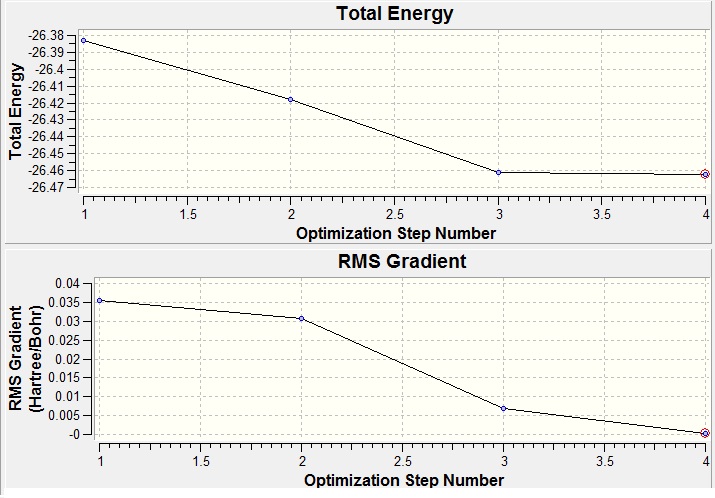
Each B-H bond was set to a length of 1.5 angstroms then the molecule BH3 was optimised using the calculation method B3LYP and the basis set 3-21G. The optimisation involves solving Schrodinger's equation for the electronic density in the molecule with an assumed position of the nuclei, then solving the nuclei by adjusting the position of the nuclei for a given electronic configuration - called optimisation steps. When there is no further decrease in energy, the geometry with the lowest energy is selected as the optimised geometry. This is shown graphically in Fig 2. The method BLYP governs the type of approximations made in solving the Schrodinger equation whilst the basis set determines the accuracy; the more accurate the basis set, the more functions included in the calculation and hence the longer the calculation takes. The basis set used in this calculation is of low accuracy but it very quick. The optimisation gave a geometry with a B-H bond length of 1.19 angstroms and a H-B-H bond angle of 120.0 degrees.The summary of the optimisation of BH3 is shown below (Fig 1). Note the energy quoted below in the summary below has an error of +/- 10 KJmol, which is equivalent to +/- 0.00381 au
Fig 1: Summary of BH3 optimisation
The calculation was shown to be successful by the RMS gradient being less than 0.001 which indicates that the placements are converged; the energy does not change for a small displacement within a given tolerance. In other words, the deviation from optimum bond length is small; the optimisation steps may be animated in Gaussview which shows the B-H bond distances shortening to 1.19 angstroms.
Fig 2(top): Total energy against Optimisation Number; Fig 3 RMS Gradient against Optimisation Number (bottom)
The outlog file for this optimisation can be viewed at http://hdl.handle.net/10042/to-5361
BH3Molecular Orbital Calculations and Analysis
The MOs of BH3 were generated by solving for the electronic structure and then viewing the check point output file, http://hdl.handle.net/10042/to-5290. The calculation used the same basis set that was used above in optimising the molecule; this ensured that the calculation was carried out with the same level of accuracy and avoided taking into consideration excited electrons. Key words "pop=full" were added to change to MO mode, and the natural bond order was set to 'full NBO'. This calculation took 0.4secs to run on SCAN and 3secs on gaussview. The computed MOs (1-8) are compared to qualitative MOs produced by a molecular orbital diagram drawn in ChemDraw.
Fig 4: LCAO and Computed Molecular Orbitals
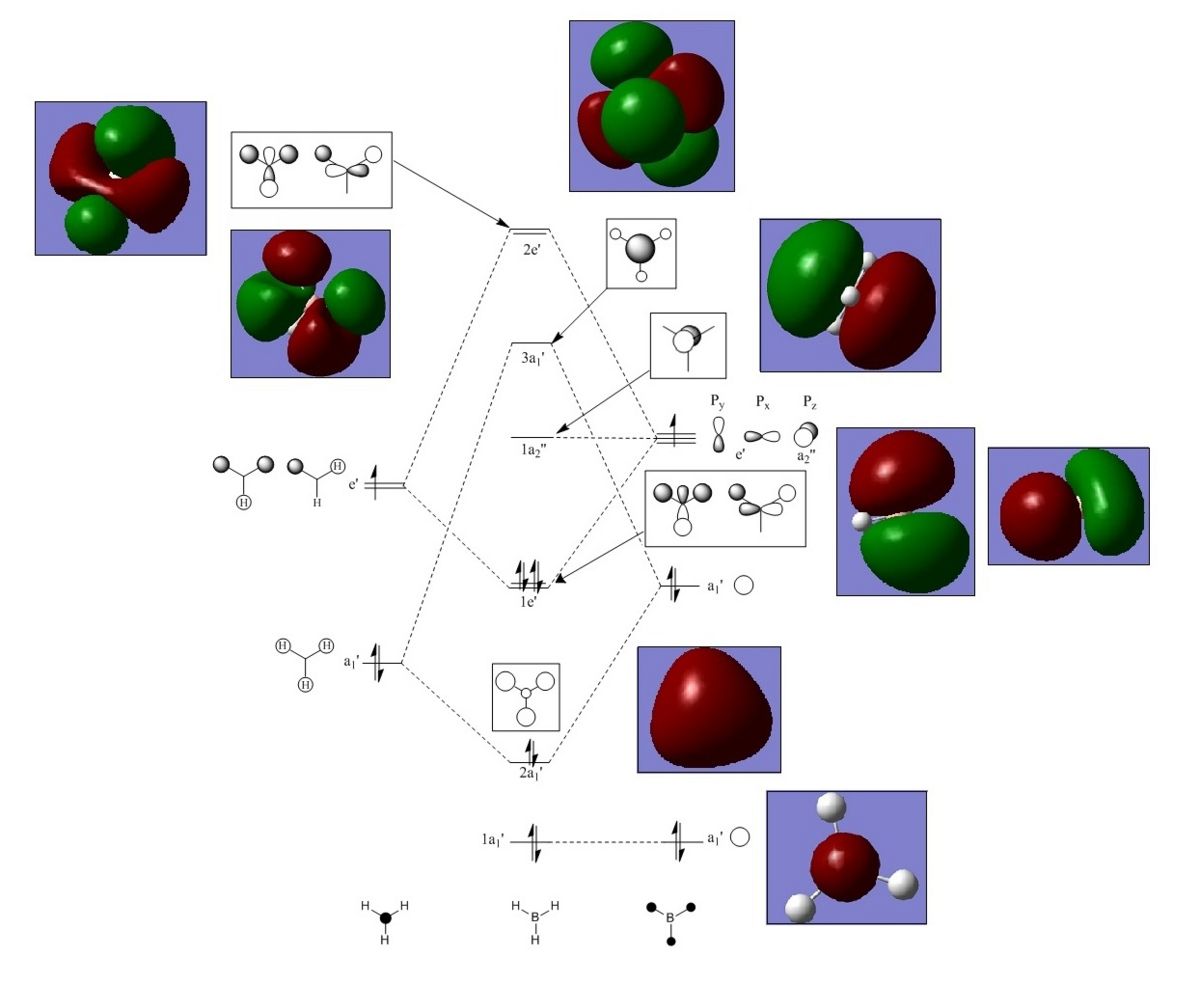
Note that 1a1 orbital lies too deep on energy to take part in the reactivity of BH3, and the unoccupied orbitals generated by Gauss view are more diffuse than the occupied orbitals.
Upon comparison, the computational results roughly correlate with the LCAO orbitals. Both sets if molecular orbitals agree in terms of the phases and number of nodes. The computational results and LCAO orbitals also differ slightly in some aspects; the computational results are smoother and more diffuse in appearance. Overall the key features of the LCAO orbitals match the computed orbitals well and there are no significant differences. This suggests that the LCAO is a good approximation for this molecule and MO theory can be very useful and accurate method for discussing the reactivity of a molecule.
BH3 NBO Analysis
Fig5: BH3 diagram showing positive and negative natural charges of each atom
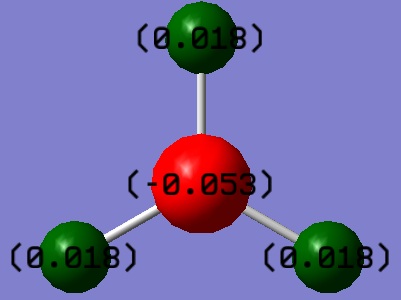
NBO analysis of BH3 was run to find out more information regarding the electron density, orbital mixing and bonding within the molecule. Firstly, NBO analysis identifies as electron deficient and electron rich atoms; bright green indicates highly positive charge and bright red highly negative charge, this can be seen in fig 5 below. The boron atom is Lewis deficient and therefore highly positively charged.
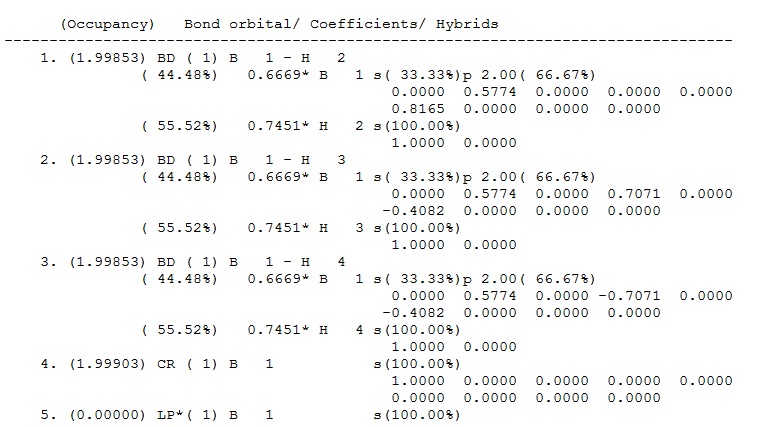
Fig 6: Contribution of each atom to MOs in BH3
NBO analysis breaks down the electron density used to make the 2e-2c bonds into contributions from each atom; this can be seen in the output file underthe heading 'Bond orbital/ Coefficients/ Hybrids' (see fig 6 above). The first three bonds are the B-H bonds, these have identical contributions; 44.49% of the bond is contributed from the B orbitals which have a hybridisation of 33%s+66%p, while 55.51% of the bond comes from the H orbital which is 100%s. This shows that B has formed three sp3 hybrid orbitals which each coordinate with the sAO of one hydrogen atom. Orbital 4 is the core (CR) 1sAO orbital of B (shown as 1a1' in the MO digram above) and orbital 5 is the boron lone pair (LP*) which is 100% p orbital - the star signifies that the orbital is formally occupied.
Under the heading 'Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis' there is normally information on MO mixing - BH3 molecular orbitals do not experience a lot of mixing.
Vibrational Analysis of BH3
When carrying out a vibrational analysis the second derivative of the potential energy surface is computed; all positive values indicate a minimum (the ground state) whilst one negative value indicates a transition state. This analysis also generated an IR (fig 8). Using the optimised structure, the vibrational frequencies were calculated, see summary box below for method details.
Fig7:Summary for BH3 frequency calculation
| Wavenumber | 1146 | 1205 | 1205 | 2592 | 2730 | 2730 |
|---|---|---|---|---|---|---|
| Vibration |  |
 |
 |
 |
 |
|
| Infra red | 93 | 12 | 12 | 0 | 104 | 104 |
| Symmetry Label | a2 | e' | e' | a1' | e' | e' |
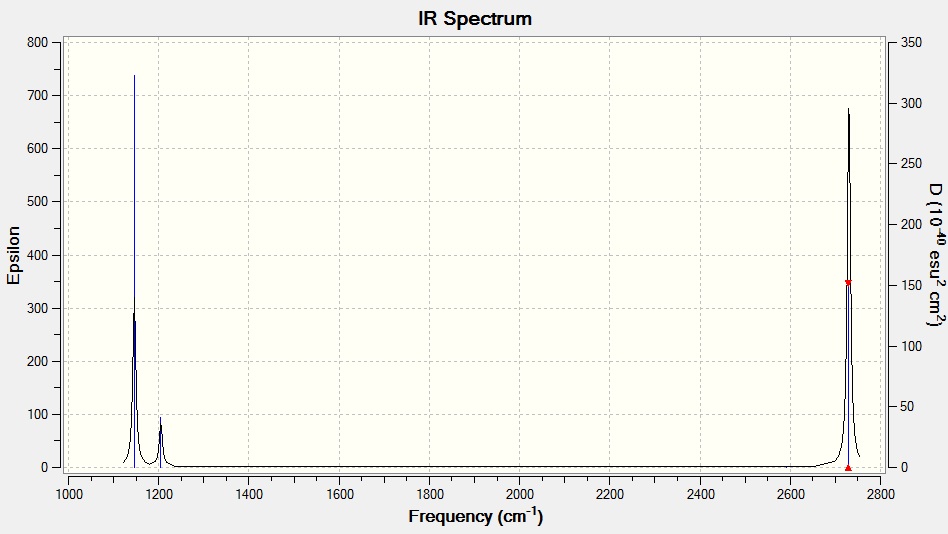
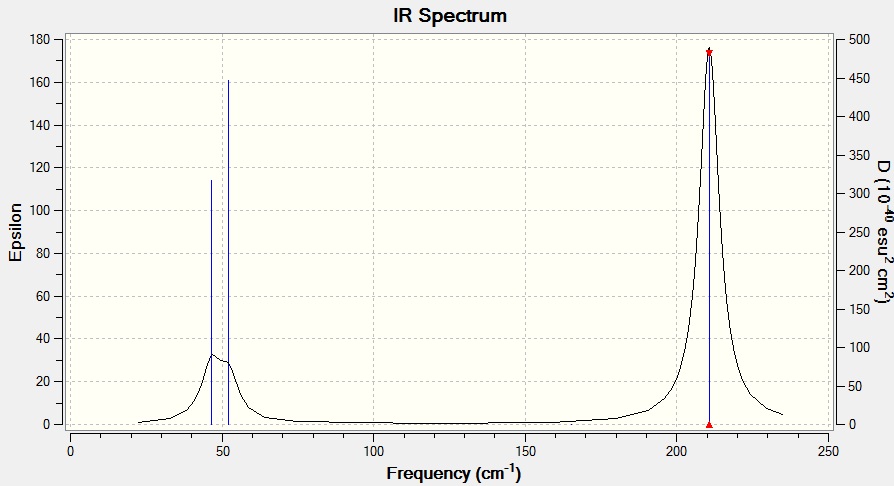
Fig 8: IR spectrum of BH3
The data above shows that the calculation was run successfully as all the frequencies are positive. As is convention, the values above are quoted to zero decimal place. There is a 10% systematic error associated with the vibrations. This error arises due to the harmonic approximation used in the calculations; the anharmonicity of the vibrations is not taken into account.
There are 6 vibrations but only three peaks present in the IR spectrum; one vibration has zero intensity since the stretch is completely symmetric and the vibration is cancelled out, there are also two sets of doubly degenerate vibrations and the corresponding peaks overlap on the spectrum.
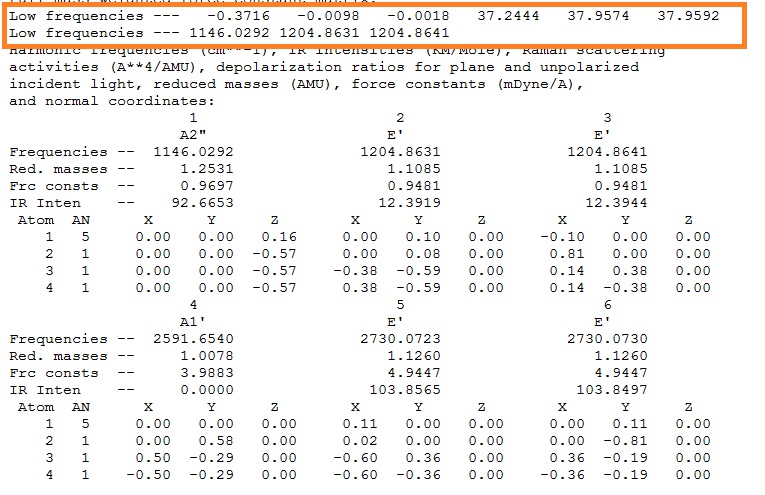
Each moleucle has 3N-6 vibrations, the "-6" frequencies(motions around the centre of mass)are highlighted below in the orange box. The more accurate the calculation, the closer the values are to zero - this calculation is not very accurate.
Fig 9: Output file showing the low frequencies
Structural Analysis of TlBr3
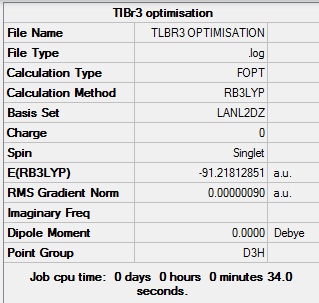
The structure of TlBr3 was optimised using RB3LYP calculation method and LANL2DZ basis set, to give a Tl-Br bond distance of 2.65 angstrom and a Br-Tl-Br bond angle of 120.0 degrees; this bond length is fairly close to the literature [1] value of 2.50 Angstrom.
Fig 10: Summary of TlBr3 optimisation
| Wavenumber | 46 | 46 | 52 | 165 | 211 | 211 |
|---|---|---|---|---|---|---|
| Vibration |  |
 |
 |
 |
 |
|
| Infra red | 4 | 4 | 6 | 0 | 25 | 25 |
Fig 11: IR sepctrum of TlBr3
The same method and basis set must be used for both calculations so that the calculations are completed to the same level of accuracy and the results are comparable i.e. changing the method and basis set would change the approximations used and the results could not be compared. Frequency analysis is a useful tool; it is carried out to confirm that the minimum structures have been found. The six low frequency vibrations are -3.4213, -0.0026, -0.0004, 0.0015, 3.9367 and 3.9367, see fig 12. This calculation is more accurate than the one used for the vibrational analysis of BH3 since the values are closer to zero. The lowest normal mode is 46 cm-1.
What is a bond?
Within Gaussview the definition of a bond is based on units of length; if the length of a bond exceeds the set bond length the programme does not recognise the bond and it disappears! As seen with the Mo isomers below after optimisation. A bond is a region of electron density between two atoms and is held together by attractive forces. The first scientist to define the nature of a chemical bond, Linus Pauling, describes it as forces acting between atoms that lead to the formation of an aggregate with sufficient stability to make it convenient for chemists to consider it as an independent molecular species. [2] The output files: media:TLBR3_OPTIMISATIONcfl08.LOG media:TLBR3_FREQcfl08.LOG
Fig 12: Low frequencies of TlBr3
Isomers of [Mo(CO)4(PCl3)2]
The phenyl ligands in the trans and cis isomers of [Mo(CO)4(PPh3)2] were replaced by electronically similar Cl ligand; using a smaller ligand simplifies the computational calculations and decreases the time taken to run the calculations. The isomers were optimised twice and the vibrational modes of each isomer were computed.
The structure of cis- and trans-[Mo(CO)4(PCl3)2] was first loosely optimised using the B3LYP method, a pseudo-potential of LANL2MB and setting the convergence criteria to loose by adding "opt=loose" to the additional keywords. Note, this resulted in bonds missing from the optimised structure - reasons for this are discussed above in the 'what is a bond?' section. It is possible to fall into local minima rather than acquiring the lowest energy structure if the calculation isn't carried out on the right orientation therefore both isomers were then manually manipulated. The trans isomer was orientated so that the PCl3 groups were eclipsed and one Cl of each group lied parallel to one Mo-C bond. The cis isomer was orientated so that one Cl points up parallel to the axial bond and one Cl of the other group points down. The structures were then optimised for a second time using the B3LYP method with the LANL2DZ pseudo-potential and basis sets with the additional words "int=ultrafine scf=conver=9" to give a tighter convergence.
The output files can be viewed through these links: Trans opt 1 - [1] Trans opt 2 - [2] Cis opt 1 - [3] Cis opt 2 - [4]
Comparing the computed cis and trans geometries
| Trans - opt 1 | Trans - opt 2 | Cis - opt 1 | Cis - opt 2 | |
|---|---|---|---|---|
| Energy/ au | - 617.52 | -623.58 | -615.89 | -622.00 |
In the loose and ultra optimisations, the trans isomer has a lower energy. This could be due to the PCl3 groups being more bulky than the CO groups; in the trans conformer they are further apart and therefore it is more sterically favourable. If the R group was smaller in size, maybe the cis isomer would be more stable. The difference in energy between the final optimised structures is 1.58 au (4148.29 K/Jmol) this is a large energy difference - bigger than expected. This shows the limitations of the method and basis set used. It is also possible that the optimised cis isomer in these results is incorrect and that the calculation fell into a local minima which is easy to do with these types of calculations. The final optimised geometries are compared to literature values below.
| Computed Trans | Literature [3] | Computed Cis< | literature [4] | |
|---|---|---|---|---|
| Mo-P/Angstrom | 2.45 | 2.50 | 3.86/2.61 | 2.58 |
| Mo-C/Angstrom | 2.06 | 2.01 | 1.96/2.02 | 1.97/2.06 |
| P-Mo-P/degree | 180 | 180 | 113.1 | 94.8 |
| C-Mo-C/Angstrom | 89.5/179.0 | 87/180 | (1) | 83 |
| C-Mo-P/Angstrom | 88.7/180 | 87/180 | (2) | 91.7/173.2 |
(1)The angle varied depending on which C-Mo-C bond
(2) The C-Mo-P angle also varied
On comparison to literature values, the trans isomer matches well. However, it became very apparent that the cis isomer is not the correct optimised structure, which explains the bug difference in energy seen above. Most noticeably, the Mo-P bonds are of different lengths! On closer inspection, it was noticed that the calculation did not completely converge. There was not sufficient time to re-run this calculation to gain the correct result; since this is the wrong structure the frequency analysis did not work and it is not included in the discussion below. The first optimisation of the cis-isomer did completely converge - therefore the structure must have been changed by mistake whilst trying to manually change the orientation of the PCl3 groups.
IR spectra
Trans Isomer
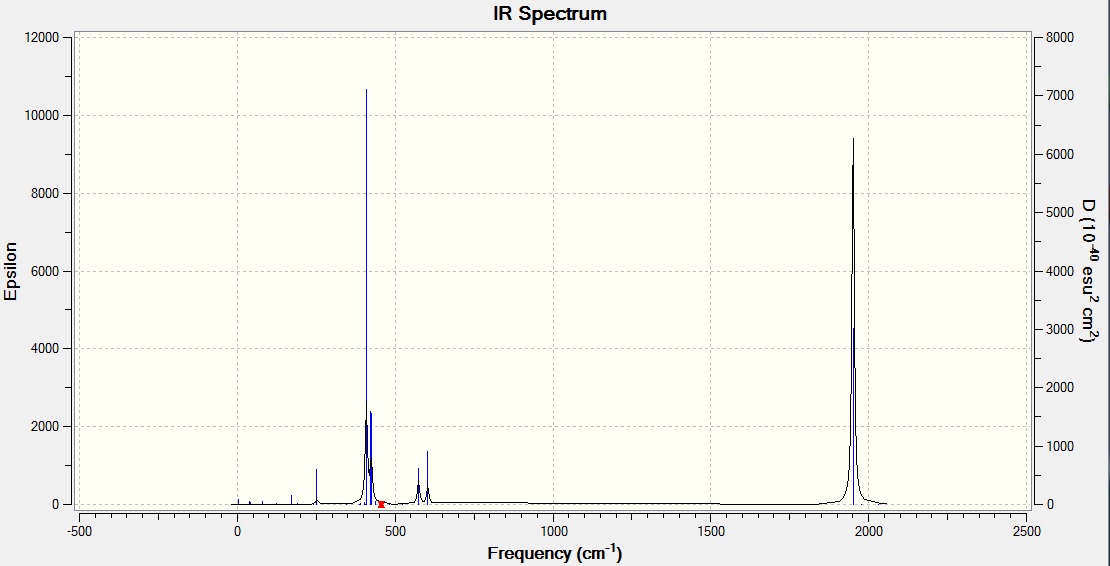
One peak is seen on the trans isomer spectrum. The C2v cis-isomer has the irreducible representation 2A1+B1+B2 - all four of the contributing species are infra-red active. Where as for the D3h trans-isomer, the irreducible representation = A1g +B1g +Eu, where only the Eu mode is infra-red active therefore only one band is seen. A vibration is not infra-red active if the vibrational movements cancel each other out due to the symmetry.
The CO stretch is seen at 1951 cm-1 which is fairly close to literature value [4] of 1901 cm-1 and to the experimental value [5] of 1890 cm-1 found last year in inorganic lab. The difference is due to the calculation not taking into account anharmonicity of the vibrational movement. Although it was not possible to generate a cis-isomer IR (explained above) four bands would be expected; the spectra however would only have two peaks at 2023 and 1897 cm-1 [4] as B1, A1(1) and B2 overlap. Last year, from synthesing these molecules in inorganic practical inorganic lab, two stretches at 2012 and 1888 cm-1 were seen[5].
Output files: opt 1 trans -http://hdl.handle.net/10042/to-5308 opt 2 trans - http://hdl.handle.net/10042/to-5309 freq trans - http://hdl.handle.net/10042/to-5521 opt 1 cis - http://hdl.handle.net/10042/to-5428 opt 2 cis - http://hdl.handle.net/10042/to-5429
Mini Project: Phosphazenes and P-N linkages
The cyclic trimer (NPCl2)3 is a well known inorganic ring and is the focus of this mini project. The structure was optimised, the vibrations analysed and then MOs generated. The Cl atoms were then substituted for Br and NH2 groups; the effect on the energy and frequency analysis was examined. For each calculation the electron basis set 6-311G(d,p) and B3LYP was used.
MO and frequency Analysis
| (PNCl2)3 | (PNBr2)3 | (PN(NH2)2)3 | |
|---|---|---|---|
| Optimised Structures | |||
| Energy au | -3949.91 | -16633.44 | -1524.41 |
| P-N bond lengths in ring/Angstrom | 1.59 | 1.60 | 1.61 |
| P-X lengths/ Angstrom | 2.04 | 2.22 | 1.69 |
As expected, all optimised geometries are planar. In order of stability the Br trimer > Cl trimer > NH2 - this can be reasoned by NH2 being the most bulky group, P is an electropositive element therefore it will be more destabilised attached to a Cl atom as Cl is more electron withdrawing than Br. P-N lengths in the ring are all equal and between a single and double phosphorous- nitrogen bond.
| (PNCl2)3 | Literature | (PNBr2)3 [6] | Literature [6] | Vibrational movement |
|---|---|---|---|---|
| 769 | 786 | 737 | 755 | Ring stretching (a'1) |
| 654 | 669 | 631 | 641 | Ring bending(a'1) |
| 343 | 365 | 206 | 221 | PX2 sym. stretching (a'1) |
| 168 | 174 | 96 | 102 | PX2 sym. bending (a'1) |
| 1224 | 1219 | 1099 | 1179 | Ring stretching (e') |
| 856 | 880 | 829 | 840 | Ring stretching(e') |
| 506 | 529 | 437 | 444 | Ring bending, in-plane (e') |
| 342 | 337 | 247 | 257 | PX2 sym. stretching(e') |
| 168 | 188 | 130 | 128 | PX2 wagging (e') |
| 151 | 160 | 87 | 94 | PX2 bending (e') |
| 549 | 540 | 470,471 | 535,544 | Ring def. out-of-plane (a2") |
| 608 | 602 | 538 | 475 | PX2 asym. stretching (a2") |
| 212 | 218 | 139 | 147 | PX2 rocking(a2") |
| 608 | 580 | 438 | 488 | PX2 asym. stretching(e) |
| 311 | 303 | 248 | 284 | Ring def out-of-plane (e) |
| 192 | 204 | 131 | 140 | PX2 rocking(e") |
The frequency values are similar but not exactly matching the literature values; the difference is due to the approximations made in the calculation to generate the vibrations. The results could be improved by using a more accurate basis set.
The frequency analysis of the (PN(NH2)2)3 trimer gave some negative frequencies suggesting that the structure used is not the optimised structure despite the fact that it completely converged, and the the low frequencies obtained from the frequency analysis are close to zero. This trimer was optimised again to see if a slightly different structure would be obtained however this gave the same result. The three negative frequencies are -103, -92, -85 cm-1 and the vibrational movement shows the NH2 groups wagging. The low frequency means that this particular vibration is at a maxima. If there was more time, the geometry of the NH2 group could be manually changed and the moleucle re-optimised so that none of the frequenices are negative; since the vibrations which are negative are not important in this discussion the frequencies obtained will be compared, focussing on the P-X.
From viewing the vibrations, the symmetric P-X stretches occur at 875 and 262 cm-1 and the antisymmetric stretches are at 475 and 851 cm-1. On comparison with the P-Cl and P-Br stretches the anti-symmetrical and symmetrical stretches are in the order Cl>NH2>Br. The higher the frequency of vibration the more energy needed to vibrate the bond and therefore the stronger the bond. Stronger bonds are due to better orbital overlap. The atoms attached to the cyclic phosphorous atoms also affect the ring stretching and bending; the ring stretching and bending is consistently of lower frequency for the (PBr2)3 trimer compared to the (PCl2)3 trimer.
The phosphorous d(pi) and nitrogen d(pi) overlap to give a sp2 hybridised nitrogen and sp3 hybridised phosphorous. The sigma framework makes use of 2 nitrogen sp2 and 4 phosphorous sp3 orbitals. The non-bonding sp2 orbital on nitrogen is occupied by a lone pair. The Pz orbital on the nitrogen is available for further pi-interaction with dxy and dyz of phosphorous. Illustrated in the table below is the HOMO, LUMO and an interesting looking orbital (MO ).
| HOMO | LUMO | LUMO+3 |
|---|---|---|
 |
 |
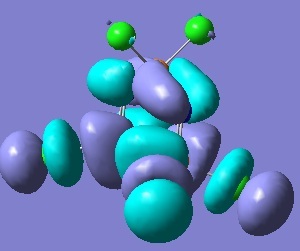
|
out put files:
Cl trimer opt - http://hdl.handle.net/10042/to-5456
Cl trimer MO - http://hdl.handle.net/10042/to-552
Cl trimer freq -http://hdl.handle.net/10042/to-5501
Br trimer opt - http://hdl.handle.net/10042/to-5523
Br trimer freq - http://hdl.handle.net/10042/to-5524
NH2 trimer opt -http://hdl.handle.net/10042/to-5525
NH2 trimer freq - http://hdl.handle.net/10042/to-5526
References
- ↑ J. Am. Chem. SOC. 1995,117, 5089
- ↑ Linus Pauling, The nature of the chemical bond, 1989 10
- ↑ Inorganica Chiraica Acta, 1997 254 167-171
- ↑ 4.0 4.1 4.2 Inorg. Chem., 21, 1982 294-299 Cite error: Invalid
<ref>tag; name "four" defined multiple times with different content - ↑ 5.0 5.1 C Lawton, Synthesis Lab Year 2, Experiment 5s 2010
- ↑ 6.0 6.1 Spectrochimica Acta, 1973 29A 1077-1083