Rep:Mod:Ceh15itmm
Optimisation using GaussView
NH3 Optimisation
The following are the results of the optimisation of ammonia (NH3) using the GaussView and Gaussian programs.
| Point Group | C3v |
| N-H Bond Length | 1.01798Å |
| H-N-H Bond Angle | 105.741° |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy | -56.55776873a.u. |
| RMS Gradient | 0.00000485 |
The following is an "Item" table produced by Gaussian. This is used to check that the values have converged to an equilibrium, and can be used as a check that the optimisation worked and is accurate. The end column shows that all the values converged, and the result can be trusted.
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Fig.1: Ammonia |
The optimisation file for the animation in fig.1.
Vibrations

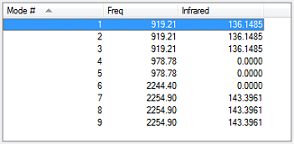
From the 3N-6 rule, I expect there to be six modes of vibration. From the table (fig.2) it can be seen that there are two pairs of degenerate modes (modes 2 and 3, and modes 5 and 6). Modes 1, 2 and 3 are bending vibrations, and modes 4, 5 and 6 are bond stretching vibrations. Mode 4 is highly symmetric. The umbrella mode is mode 1. In an experimental spectrum of gaseous ammonia, I would expect to see two bands, since the intensities of modes 4, 5 and 6 are too small to be seen alongside modes 1, 2 and 3.
Charge
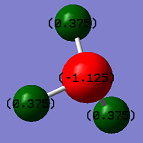
The charge on the N atom is -1.125, and the charge on each H atom is 0.375. I would expect a negative charge on the N atom and positive charges on the H atoms since nitrogen is more electronegative than hydrogen, and so will draw electron density towards itself.
N2 Optimisation
The following are the results of the optimisation of nitrogen (N2) using the GaussView and Gaussian programs.
| Point Group | D∞h |
| N-N Bond Length | 1.10550Å |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy | -109.52412868a.u. |
| RMS Gradient | 0.00000060 |
The following is an "Item" table produced by Gaussian.
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Fig.4: Nitrogen |
The optimisation file for the animation in fig.4.
Vibrations
Frequency 2457.33cm-1
There is only one frequency, which is what is expected for this molecule, as it follows the 3N-5 rule.
H2 Optimisation
The following are the results of the optimisation of hydrogen (H2) using the GaussView and Gaussian programs.
| Point Group | D∞h |
| H-H Bond Length | 0.74279Å |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy | -1.17853936a.u. |
| RMS Gradient | 0.00000017 |
The following is an "Item" table produced by Gaussian.
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Fig.5: Hydrogen |
The optimisation file for the animation in fig.5.
Vibrations
Frequency 4465.68cm-1
As with N2, there is only one frequency, which is what is expected for this molecule, as it follows the 3N-5 rule.
Haber-Bosch Energies
The following shows the process for calculating ΔEθ of the reaction to form ammonia from nitrogen and hydrogen gas.
E(NH3) = -56.55776873a.u.
2*E(NH3) = -113.11553746a.u.
E(N2) = -109.52412868a.u.
E(H2) = -1.17853936a.u.
3*E(H2) = -3.53561808a.u.
ΔE = 2*E(NH3)-[E(N2)+3*E(H2)] = -0.0557907a.u.
To convert to kJ mol-1, this result was multiplied by 2625.5, a number found on the [this Hunt Research Group page] for this lab.
ΔEθ = -146.4784829 kJ mol-1
Since ΔEθ is negative, the products are more energetically stable, i.e. ammonia gas is more energetically stable than nitrogen and hydrogen.
Molecule of Choice - Silane, SiH4
SiH4 Optimisation
The following are the results of the optimisation of silane (SiH4) using the GaussView and Gaussian programs.
| Point Group | Td |
| Si-H Bond Length | 1.48485Å |
| H-Si-H Bond Angle | 109.471° |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Final Energy | -291.88802760a.u. |
| RMS Gradient | 0.00000002 |
The following is an "Item" table produced by Gaussian.
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Fig.6:Silane |
The optimisation for the animation in fig.6.
Vibrations
From the 3N-6 rule, I expect there to be nine modes of vibration. From the table (fig.7) it can be seen that there are two triplets and one pair of degenerate modes (modes 1, 2 and 3, modes 4 and 5, and modes 7, 8 and 9). Modes 1, 2, 3, 4 and 5 are bending vibrations, and modes 6, 7, 8 and 9 are bond stretching vibrations. In an experimental spectrum of gaseous silane, I would expect to see two bands, since the intensities of modes 4, 5 and 6 are too small to be seen along side modes 1, 2, 3, 7, 8 and 9.
Charge
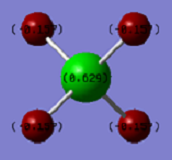
The charge on the Si atom is 0.629, and the charge on each H atom is -0.157. I would expect a negative charge on the H atom and positive charges on the Si atoms since silicon is less electronegative than hydrogen, and so the hydrogens will pull electron density towards themselves, away from the silicon centre.
Molecular Orbitals
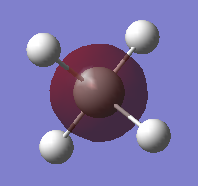





The molecular orbital shown in fig.9 consists of the 2s2 orbital of silicon. It is a non-bonding MO and very low in energy. It has no effect on the bonding in silane. As can be seen in the image, it only encompasses the silicon atom. This MO is occupied with a pair of electrons.
The molecular orbital in fig.10 consists of one of the 2p2 orbitals of silicon. Again it is a non-bonding MO. It is low in energy and, as with the 2s2, only encompasses the silicon atom. This MO is also occupied by a pair of electrons.
The molecular orbital in fig.11 consists of all four of the 1s1 orbitals of the hydrogen atoms, and the 3s1 orbital of the silicon atom. It is a bonding orbital and is fairly low in energy. This orbital is also occupied by a pair of electrons.
The molecular orbital in fig.12 consists of a mixture of 3p orbitals from silicon and 1s orbitals from the four hydrogens. This orbital is one of three similar orbitals which are degenerate. It is a bonding orbital and it is, alongside its similar degenerage MOs, the HOMO. This MO is occupied by a pair of electrons.
The molecular orbital in fig.13 consists again of a mixture of 3p orbitals from silicon and the 1s orbitals of the four hydrogens. This orbital is also one of three similar degenerate orbitals. It is an antibonding orbital and it is, alongside its similar degenerage MOs, the LUMO. This MO is unoccupied, and is the antibonding counterpart of the MO depicted in fig.12.
The molecular orbital in fig.14 consists again of a mixture of the 3s orbital from silicon and the 1s orbitals of the four hydrogens. It is an antibonding orbital and it is high in energy. This MO is unoccupied, and is the antibonding counterpart of the MO depicted in fig.11.
