Rep:Mod:Castrovalva
Week One: DFT Studies on Group 13 Hydrides/Bromides
The molecules studied herein may be modeled quite comprehensively, affording physically useful information relating to symmetry and thermodynamic quantities, using relatively mild computational methods. Investigation of even the simplest of inorganic molecules may provide useful information; one compound investigated, BBr3, has industrial applications in the manufacture of boron crystals of extreme purity[1], and hence theoretical data relating to its stability is not without use. An account and analysis of the precise studies conducted will be presented.
BH3
Manual symmetry breaking was imposed by setting the three B-H bond lengths by 1.53, 1.54 and 1,55Å, whilst maintaining the mirror plane (ie no dihedral distortion was added). A B3LYP/3-21G level calculation adequately optimised the structure (as can be seen by inspection of the RMS gradient), yet returned a Cs point group, implying the initial perturbation had not been completely 'optimised out' so to speak. The bond lengths and angles are presented in table 1, and the standard deviations (σn-1) are 1.769*10-4Å and 1.509*10-2° respectively.
| Result | Value |
|---|---|
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -26.46226429a.u. |
| RMS Gradient Norm | 0.00008851a.u. |
| Imaginary Freq | |
| Dipole Moment | 0.0003Debye |
| Point Group | CS |
| Bond Lengths | 1.19480Å, 1.19467Å, 1.19445Å |
| H-B-H Angles | 120.016°, 119.998°, 119.986° |
| Log | File:SI BH3 OPT.LOG |
A higher optimisation was conducted using the 6-31G(d,p) basis set from the output coordinates of the previous calculation, affording a structure significantly closer to symmetric.
| Result | Value |
|---|---|
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -26.61532360 |
| RMS Gradient Norm | 0.00000707 |
| Imaginary Freq | |
| Dipole Moment | 0.0001 |
| Point Group | CS |
| Bond Lengths | 1.19231Å, 1.19231Å, 1.19232Å |
| H-B-H Angles | 120.001°, 120.001°, 120.002° |
| Log | File:SI BH3 OPT 631.LOG |
Frequency
Frequency analysis is very useful as an aid to synthetic chemistry, allowing precise attribution of modes in a synthesised molecule, or even aiding in assessment of the success of a synthesis. In a more theoretical sense, a frequency analysis allows us to determine whether an optimisation has provided us with useful atomic coordinates, as properties of the output spectrum can be compared to the recorded. If;
- there are fewer/more peaks
- there are large inaccuracies in peak energies/absorbances
Then one may conclude that either the input coordinates are incorrect or the calculation is simply a too low a level to provide useful information.
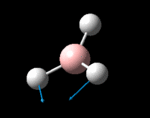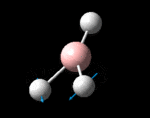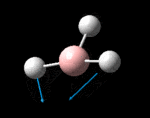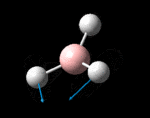
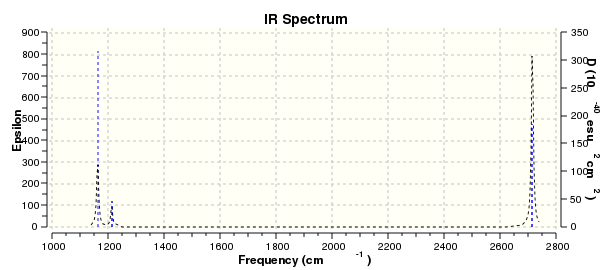
The molecule was symmetrised to the D3h point group (very tight) and a frequency calculation performed, once again to the B3LYP/6-31G(d,p) level. The output frequencies of the two strongest bands (1163 and 2716cm-1) were consistent with those known[2] (deviations of 33.8 and 128.3cm-1) and information was returned on the weak/symmetry disallowed bands at 1213 and 2582cm-1. These deviations may be significant (and indeed it should not be stated that this calculation is inherently accurate with respect to the energy of the transitions), but they are smaller than similar calculations conducted in the referenced work, done with MBPT(2)/TZP theory/basis set (whose deviations were 66.0 and 187.8cm-1). There is, of course, some room for isotope shifts in the observed spectra which are not accounted for in the calculation (Gaussian simply assumes the most common isotope - in this case 11B) but is likely to be a negligible effect with respect to predicted frequencies.
| Symmetry Label | A2"
|
E'
|
A1
|
E'
|
|---|---|---|---|---|
| Identity | 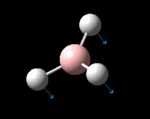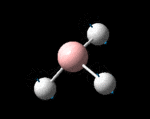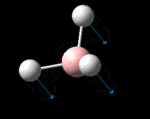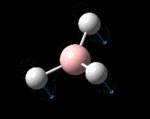 |
  |
 |
  |
| Predicted Frequency/cm-1 | 1162.96 | 1213.16, 1213.16 | 2582.39 | 2715.57, 2715.57 |
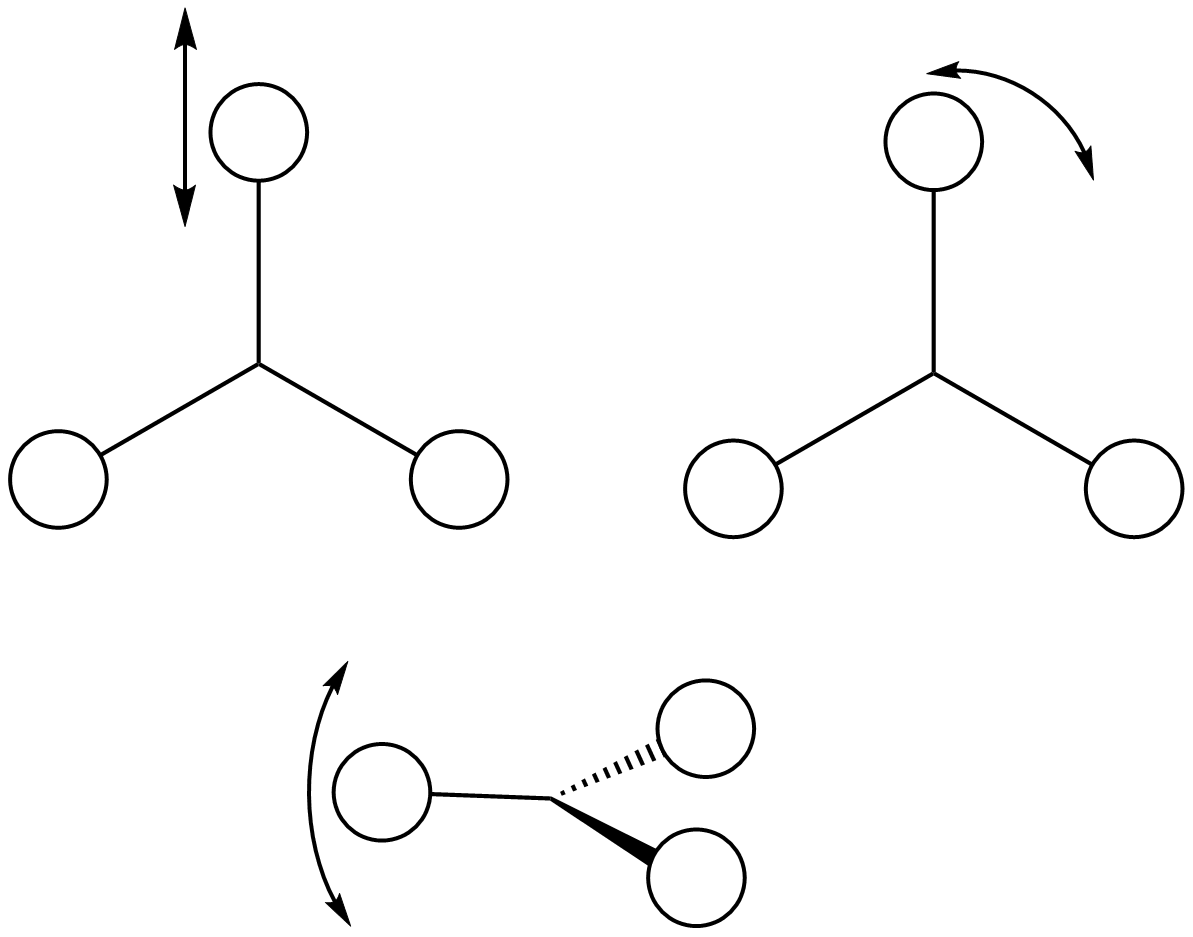
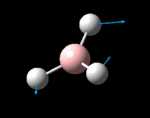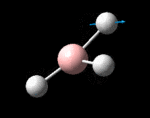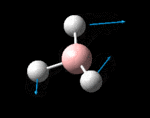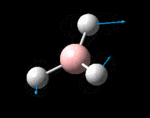
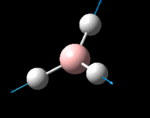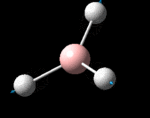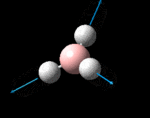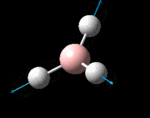
The possible symmetry labels of the ν modes are defined by the point group in much the same way molecular orbitals can be assigned (and indicates why we have forced D3h symmetry earlier). The basis vectors from which we can investigate the identity of the computed modes are shown in figure 1. Each of the three vibrations can be combined using group theory, provided we discount those that do not result in any distortion of the molecules bonds: the fully symmetric in plane wagging mode is merely a rotation about the z axis, and both antisymmetric combinations of the out of plane wagging are oscillating rotations about the x and y axes (and hence involve no change in force constants). Therefore, of the available nine, only six combinations of vectors are actually vibrations (which is consistent with 3N-6 modes for a non linear molecule).
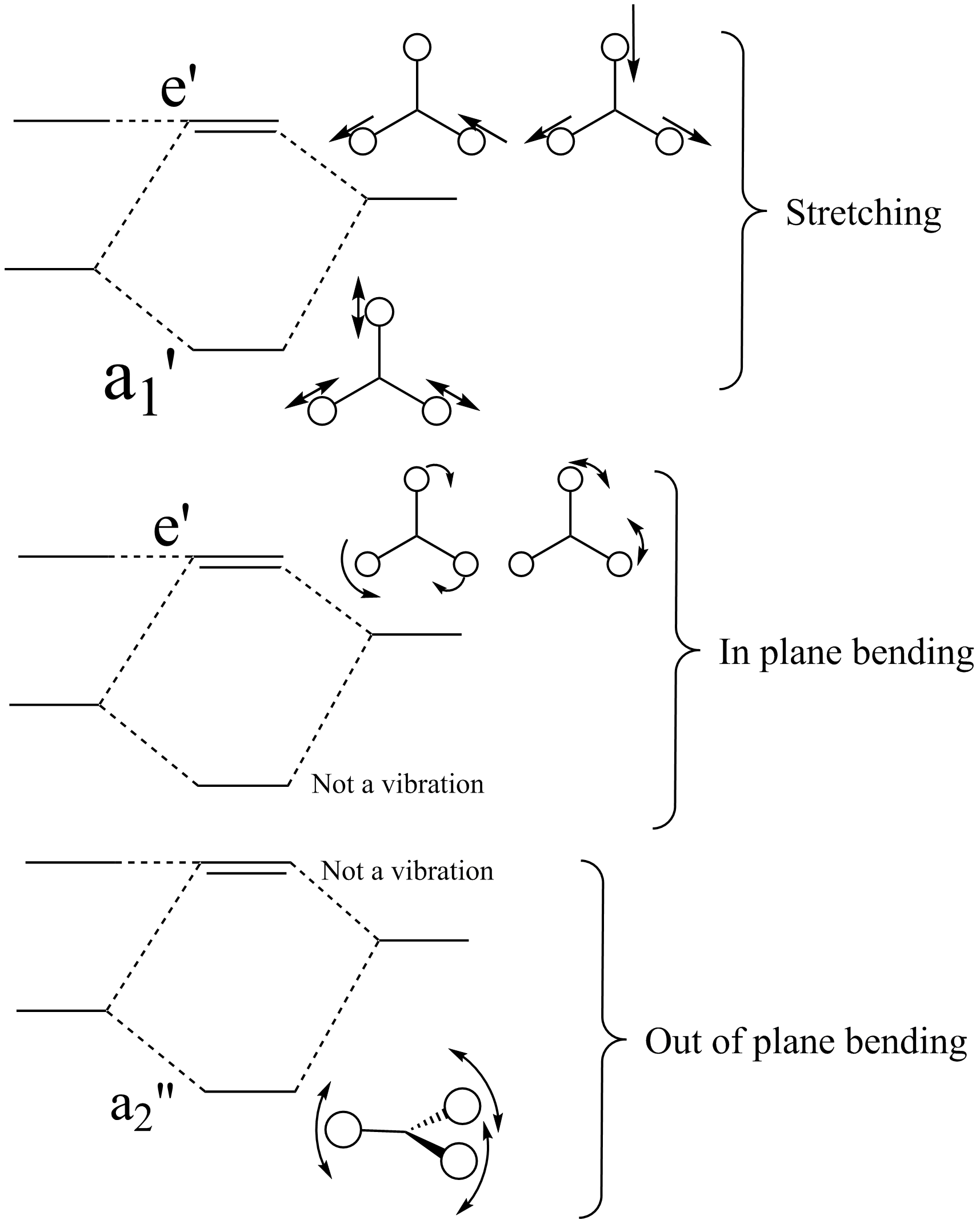
However, the predicted spectrum only contains three absorptions; two of the 'missing' peaks are accounted for by degeneracy in the e' modes, and the third (the A1' mode) is disallowed, as it does not alter the dipole of the molecule. The closeness of the different bending modes to each other and the higher energy of stretching has been approximated by figure 2, . The 'low frequencies' returned in the log file but not rendered by Gaussview correspond to the fingerprint region, and should be payed significant attention in these treatments: large values imply the molecule is susceptible to complex perturbations at low energy levels and hence may be mechanically unstable.
| Result | Value |
|---|---|
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -26.61532363a.u. |
| RMS Gradient Norm | 0.00000729a.u. |
| Imaginary Freq | 0 |
| Dipole Moment | 0.0000Debye |
| Point Group | D3H |
| Log | File:SI BH3 FREQ.LOG |
MOs
The first 8 molecular orbitals of BH3 computed to the B3LYP/6-31G(d,p)[3] level have been assessed with reference to a qualitative MO picture constructed from a similar H3 like fragment to that utilised in the vibrational analysis earlier (figure 2). The most obvious deviation in apparent electron density is that of the orbitals comprising the bonding E' level, which appear to be identical in distribution, with nonzero orbital coefficients on all four atoms, yet one is displaced 120° relative to the other. The frontier orbital prediction is partly correct as the computed orbitals contain one node each but fails to predict both having electron density on all of the 'ligand' hydrogens.

It can be stated that a common feature of the orbitals provided by this calculation are unpredictable coefficients; for example the formally non-bonding A2" orbital (simply a B(pz) orbital) is much wider than one may initially expect, spread over all four atoms. Similarly the σ antibonding orbital 6 contains drastic deviations from spherical distributions in all atomic orbitals, with the B(2s) appearing almost cylindrical. All other orbitals are as expected, although the inclusion of the B(1s) atomic orbital should be noted, as it is often neglected from many frontier orbital treatments.
The antibonding E' level is perhaps the furthest qualitatively away from that predicted, although unoccupied orbitals are often found to be less accurate in these kinds of calculations. As can bee seen from fig. 4, one of the hydrogens has nodal planes intersecting its nucleus, implying some kind of p character originating from this atom. Little explanation can be offered beyond that just mentioned, and that the high energy of the orbital suggests a large antibonding character, perhaps distorting the H(1s) orbital such that it appears as a p-function like lobe.
Supplementary information
B3LYP/3-21G Opt
Item Value Threshold Converged? Maximum Force 0.000220 0.000450 YES RMS Force 0.000106 0.000300 YES Maximum Displacement 0.000919 0.001800 YES RMS Displacement 0.000447 0.001200 YES
B3LYP/6-31G(d,p) Opt
Item Value Threshold Converged? Maximum Force 0.000012 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000061 0.001800 YES RMS Displacement 0.000038 0.001200 YES
B3LYP/6-31G(d,p) Freq
Item Value Threshold Converged? Maximum Force 0.000015 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000057 0.001800 YES RMS Displacement 0.000029 0.001200 YES
BBr3 and GaBr3: Structure Comparisons
The consequences of altering the central, and ligand, atoms on the bond lengths of trivalent group XIII compounds have been investigated, beginning with the 6-31G(d,p) optimisation of borane enumerated earlier. All calculations were performed with very tight constriction of the point group to D3h. Boron atoms were treated with 6-31G(d,p) basis sets, whereas all Bromine/Gallium atoms with LanL2DZ pseudo potentials.
| Compound | |||
|---|---|---|---|
| BH3 | BBr3 | GaBr3 | |
| Bond Length/Å | 1.19230 | 1.90248 | 2.35081 |
The most useful starting point for this treatment are comparisons with the sums of covalent radii, as all bonds are single and may allow us to quantify the improvements calculations have afforded over a crude model. The values used have been taken from a recent metastudy[4] conducted with reference to the Cambridge structural database, and propose bond lengths of 1.15, 2.04 and 2.42Å respectively. The first conclusion to be drawn from this is the degree of overestimation covalent radii afford increases with proportion of heavy atoms present. This may be due to the nature of bonds occurring in the CCDC, C-B and C-Br will predominate over B-Br.
We can state with certainty that the increase when altering the 'ligand' from H to Br is a manifestation of the differing orbitals undertaking bonding ie. 1s vs 4p (even considering the much larger nuclear charge contracting the atomic size in the latter case), combined with the large energy differences between frontier orbitals reducing the degree of bonding. Hydrogen may be less electronegative than Bromine but this is not an appreciable effect given the differences in the radial distribution maxima for the two interacting orbitals in these atoms.
The most obvious discrepancy between consideration of Boron and Gallium central atoms is that Ga has a filled 3d orbital. Although in a sense the calculations for BH3 and BBr3 include d orbitals on boron (as polarisation functions), this is not believed to have as large an impact on the result as approximating a filled sub shell energetically below the frontier orbitals with a pseudopotential. It must be stressed that this is not to discredit this computation type; there is a precedent for its use with gallium-p block compounds to provide physically useful results in the literature[5]. The Gallium-Bromine bond is also very polarised (mulliken charges +0.633 and -0.211), and this may account for the contraction observed relative to simple covalent radii treatment. Unfortunately a comparison to the Boron-Bromine bond polarity cannot be made in this case as differing basis sets must be used for each atom, meaning the calculation does not return this data. Qualitatively we would expect it to be less polarised however, by simple electronegativity considerations.
The effect that the metaphors by which modelling software display molecules have on the conclusions that the computational chemist may draw should not be underestimated. Gaussview is inherently reductionist in this respect, especially in its conditional drawing of bonds between atoms when rendering computational outputs. This can be most readily seen in the varying optimisation steps on the perturbed BH3, in which bonds are only formally drawn after the second step. This is, of course, a layer of interpretation that the program is providing entirely separately from the quantum mechanical information is it being given by Gaussian. A much more objective method by which the existence of bonds can be determined is Quantum Theory Atoms In Molecules (QTAIM)[6], which identifies points of inflection in electron density, and can often lead to the identification of entirely non trivial bonding interactions.
One should, of course, also define precisely what we mean by 'bond'. This is undoubtedly a continuum but there are two extreme definitions that, in the authors personal opinion, capture the majority of quantum effects known to be bonds but exclude the majority that aren't. They can be relayed as:
- A constructive interaction of two or more occupied atomic orbitals over two or more atoms, leading to an overall attractive electrostatic force, as defined by a Morse/Lennard Jones potential
- A region of increased electron density between nuclei relative to the vacuum
These are still non ideal: 1 could easily be a description of a molecular orbital, and also makes no mention of electrons. Furthermore, the theoretical chemist does not need to go to particularly extravagant molecules to find ostensibly bonding interactions which arise from destructive overlaps of AOs (the HOMO of carbon monoxide for example). 2 suffers the opposite problem and is over-prescriptive, including the concept of ring critical points which are definitely not bonds. Nevertheless these are presented as 'least bad' definitions.
BH3 and GaBr3 Frequency Comparisons
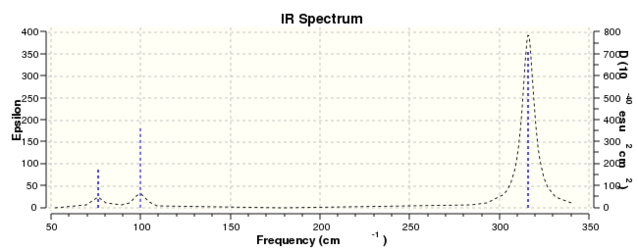
Beyond initial optimisation, frequency calculations on GaBr3 were not found to converge using LanL2DZ basis/pseudopotentials unless Opt+Freq were conducted simultaneously (specifying LanL2DZ pp for each atom under gen simply caused the calculation to fail). Nonetheless the output IR spectrum shows some interesting features when comparing to BH3. We will split considerations into identity and ordering/energy.
Identity
Much like the BH3 spectrum there exist an A1', A2 and two E' modes which can be found in the table below. This is not controversial to an extent (given the tightness of point group imposed), although it is immediately of note that the 'lever points' of the bond stretches for GaBr3 are much further away from the central atom, and the gallium undergoes quite a large displacement along the z axis in the A2 mode. This is a manifestation of the differing center of mass of the bonds.
| Symmetry Label | E'
|
A2"
|
A1
|
E'
|
|---|---|---|---|---|
| Identity |   |
 |
 |
  |
| Predicted Frequency/cm-1 | 76.37, 76.38
|
99.70
|
197.34
|
316.18, 316.19
|
Ordering/Energy
With reference to figure 2 earlier, we may see that there has indeed been a reordering, principally that the in plane vibrations now occur at lower energy than the out of plane. This may be related to the center of mass argument mentioned earlier, in that all four atoms are now oscillating relative to the plane of the molecule, whereas in BH3 this was merely confined to the hydrogen atoms, and less energy was needed to drive it. A corollary to this may be used to explain why the energy levels for GaBr3 are lower in the first place: assuming that the force constant of a B-H bond if of a similar order of magnitude to that of a Ga-Br bond, the frequency of oscillation is defined by: which will be lower purely by inspection of the masses (and we may finally convert to wavenumbers by dividing by the speed of light). Finally, the extinction coefficients are of note here, in that the A2" mode is a significantly smaller transition relative to the E' stretches, and all modes occur at lower intensities than those of BH3.
Supplementary Information
BBr3 B3LYP/Gen Opt
| Result | Value |
|---|---|
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | Gen |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -64.43645296a.u. |
| RMS Gradient Norm | 0.00000069a.u. |
| Imaginary Freq | |
| Dipole Moment | 0.0000Debye |
| Point Group | D3H |
| File | File:SI BBr3 GEN.out |
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000006 0.001800 YES RMS Displacement 0.000004 0.001200 YES
GaBr3 B3LYP/LanL2DZ Opt
| Result | Value |
|---|---|
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -41.70082783a.u. |
| RMS Gradient Norm | 0.00000016a.u. |
| Imaginary Freq | |
| Dipole Moment | 0.0000Debye |
| Point Group | D3H |
| Logfile | File:SI GaBr3 Opt.log |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES
GaBr3 B3LYP/LanL2DZ Opt + Freq
| Result | Value |
|---|---|
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -41.70082783a.u. |
| RMS Gradient Norm | 0.00000016a.u. |
| Imaginary Freq | 0 |
| Dipole Moment | 0.0000Debye |
| Point Group | D3H |
| Logfile | File:SI GABR3 FREQ.LOG |
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES
NH3-BH3
Discounting transition state considerations, a large amount of information regarding the formation and stability of certain species can be gained simply by subtraction of output energies, provided they are computed to the same level/basis set. The lewis acid/base adduct of borane with ammonia offers a computationally non intensive assessment of this.
To begin with an Opt/Freq on ammonia was conducted straight away at the 6-31G(d,p) level and was found to converge quite easily[7]. Further to this, an nbo(pop,full) calculation[8] was specified and the output charge distribution presented below.
As only energy is needed beyond this point, and we have simulated BH3 to precisely this level previously, only an H3N→BH3 OptFreq is needed[9].
| Result | Value |
|---|---|
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -83.22468921a.u. |
| RMS Gradient Norm | 0.00001459a.u. |
| Imaginary Freq | 0 |
| Dipole Moment | 5.5642Debye |
| Point Group | C1 |
As expected, the energy of the adduct is more negative than the total of the two hydrides (in units of hartrees), and we may be able to calculate an association/dissociation energy:
This is within an order of magnitude to that determined previously in the literature[10] for dative N→B bonds (45.7% relative error) averaged over a sample of similar molecules. The simple nature of the adduct implies that the largest enthalpic contribution to this association energy will simply be this bond.
- ↑ CRC, Handbook of Chemistry and Physics, 94th ed., 2013, 4-6
- ↑ T.J. Tague Jr., L. Andrews, J. Am. Chem. Soc., 1994, 116(11), 4970
- ↑ S. Ingram, 2014, DOI:10042/27711
- ↑ B. Cordero, V. Gomez, A.E. Platero-Prats, M. Reves, J. Echeverria, E. Cremades, F. Barragan and S. Alvarez*, Dalton Trans., 2008, 21, 2832
- ↑ B. Mondal, D. Mandal, D. Ghosh, and A.K. Das., J. Phys. Chem. A., 2010, 14. 5016
- ↑ R.F.W. Bader, in Atoms in Molecules - A Quantum Theory, Oxford University Press, 1990
- ↑ S. Ingram, 2014, DOI:10042/27714
- ↑ S. Ingram, 2014, DOI:10042/27715
- ↑ S. Ingram, 2014, DOI:10042/27716
- ↑ G. Leroy, M.Sana, C. Wilante, Theor. Chim. Acta., 1993, 85, 155
Supplementary Information
NH3 B3LYP/6-31G(d,p) Opt Freq
Item Value Threshold Converged? Maximum Force 0.000005 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES
NH3 B3LYP/6-31G(d,p) NBO
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
N 1 -1.12515 1.99982 6.11104 0.01429 8.12515
H 2 0.37505 0.00000 0.62249 0.00246 0.62495
H 3 0.37505 0.00000 0.62249 0.00246 0.62495
H 4 0.37505 0.00000 0.62249 0.00246 0.62495
=======================================================================
* Total * 0.00000 1.99982 7.97852 0.02166 10.00000
Week Two: DFT Studies on Tl(I) Fluoro-Triazapentadienyl complexes
Abstract
The use of fluorinated triazapentadienyl ligands to isolate main group elements in monomeric complexes has been explored synthetically in a variety of ways by Dias et. al., frequently complementing their works with simultaneous computational investigations. The currently investigated complex 1 is based on a reported[1] bismesitylene Thallium complex, and offers a wide scope of possible computation to be conducted. Fluorination level has been shown to have a radical effect on the energy and polarity of optimised structures. Quantum chemical calculations relating to the free ligands, performed at a higher level to those found in the literature, have afforded conclusions regarding the chemistry of this ligand motif which are substantially different to those arrived at hitherto.

Introduction
Fluorinated ligands are known for their ability to impart considerable stability in transition metal and (in this case) main group complexes, yet the quantum chemical reasoning for this is still the issue of some debate. They were first investigated in coordination/organometallic chemistry in the late 80s[2] and were a recurring theme in chelating scorpionate ligand chemistry[3].
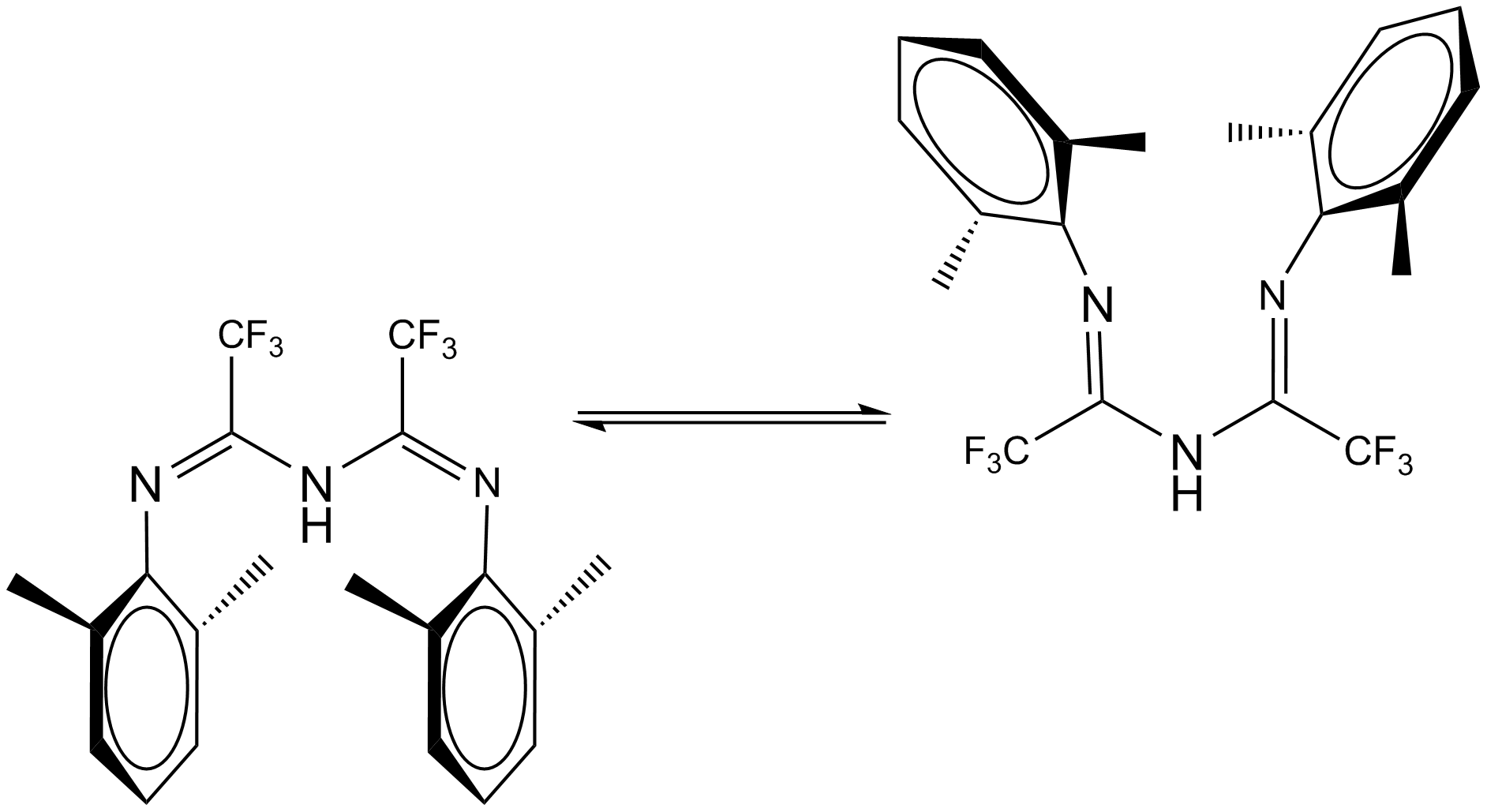
Two compounds similar to 1 (albeit with slightly more ostentatious substituents) were identified as an accessible route to deaggregation of Thallium compounds1, and were accompanied in their original reported work with computational investigation (namely UFF molecular mechanics, PM3 and B3LYP/CEP-31G(d) quantum methods), in an attempt attempt to elucidate the preferential coordination to thallium resulting in arene contacts (as drawn above). To the authors knowledge, no further or higher calculations on this precise molecule have been conducted. As such, there exist a large number of unexplored investigation pathways but presently we will restrict ourselves to:
- Finding the lowest energy conformation of the free ligand system
- Compiling overview of the dependence of stability and charge distribution on fluorination level
- Analysing the nature and enthalpic benefit of the M-Ar interactions in this molecule
To arrive at the structural formula 1 from the leading reference, any derivatives in which rotamers were present were disregarded; perfluoropropyl was replaced on the NCNCN backbone with perfluoromethyl, and 2,6-iPr with 2,6-Me. The reason for this was that while rotamer search algorithms do exist (a good example is OpenBabel[4]) and can be employed to find lowest energy conformations easily, the presence of rotationally labile chains was deemed to introduce too much uncertainty in the identity of the final optimised geometries. Similarly,The 4-methyl ring substituent was removed, but the others were not as molecular mechanics structure optimisations conducted on the crystal atomic coordinates showed that without them the rings would rotate to coplanar.
Ligand Conformations
Two competing conformations of triazapentadienyl ligands have been identified, as shown in fig. 6. Previous PM3 level calculations suggested the "U" conformation (on the right of the figure) was 0.1kcalmol-1 more stable than the "W". This was tested in this work by higher level B3LYP/6-31G(d,p) opt+freq calculations (with tight C2 symmetry imposed), the results of which are presented below.
|
|
|
|
As can be seen, not only is the W conformation lower in energy in this case, it is by 5.45kcalmol-1 (8.69*10-3Hartree). This is, of course, not the precise ligand under discussion and conformational flexibility will likely allow energetic benefits to be accrued in the alkyl chains (which are not present here), but this is a startlingly different result for a molecule that is otherwise identical. It is not, however, in contradiction with the synthetic chemistry of this area, as the W conformation of the Tl arene complex is that found by X Ray Crystallography. The significant difference in dipoles between the two conformations output in this case is predictable but would suggest a less than adequate solubility of W in solvents such as ether and hexane (which the ligand system known to dissolve in[5]) but the large size of the molecule (and its hydrophobic nature) might afford small solvent-solute repulsions. The term 'atropisomer' may be relevant to this molecule in light of this treatment but since we do not know the activation barrier little more can be said.
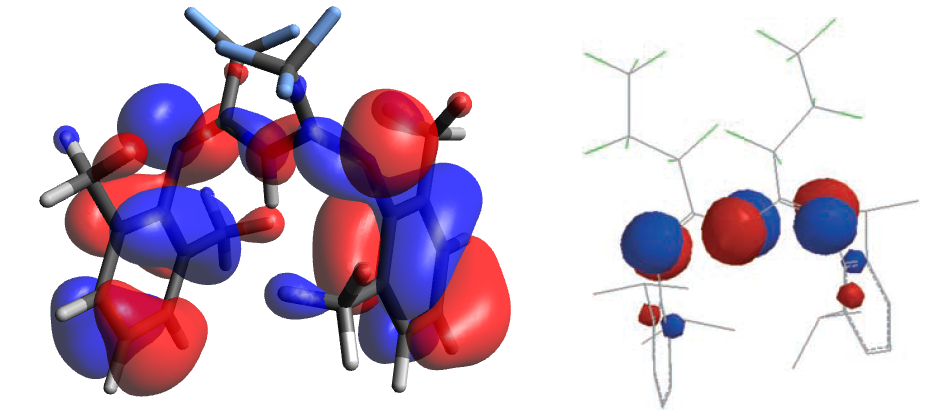
The explanation offered at the time regarding this preferential conformation (given the inverse relationship in stability) was weak Tl-η6arene contacts (ie an association energy), and the even distribution of 'donating' electron density in the ligand HOMO among the three Nitrogens. However MO surfaces provided by a freq calculation at the same level as optimisations (we will return to the IR later) do not corroborate this: The terminal imide nitrogens clearly have larger lobes than the central (fig. 7), implying their activity towards electrophiles should be higher. The orbital also contains large amounts of electron density on the aromatic rings; the presence of one node bisecting each suggests they arise from the second benzene π bonding orbital. The alterations to the ligand are unlikely to be the cause of this disagreement as very little electron density is present on any ring/chain substituents. It may be due to the fact that the PM3 calculation previously referred to was for the deprotonated (negatively charged) ligand; but the number of electrons is not changed by deprotonation; and there is no density on the N-H in the HOMO. The indication afforded by this treatment is that an investigate the stability of the perfluorinated Thallium complex in the U conformation is necessary. This will be performed towards the end of this project.
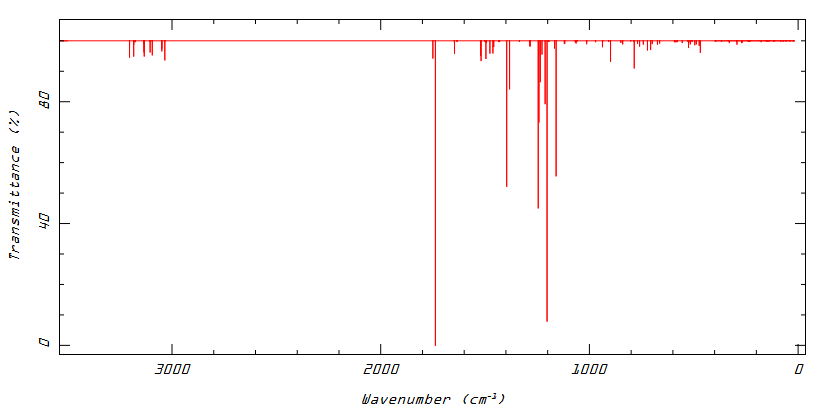
Frequency calculations relating to the differing ligand conformations appear to differentiate quite nicely between the U and W: notably, the shift of the ν(C=N) differs from 1738 in the W to 1773cm-1 in the U. There is also a large difference in extinction coefficients of the immediately preceding mode - the antisymmetric C=N stretching combination coupled to the central C-H wagging - which is much more noticeable in the U (indeed, in both cases absorbs more strongly than the ν(C=N)). The shift of the mode is larger than what is believed to be simply error in the frequency calculation and hence could be useful in identifying the predominant structure of the ligand system in a synthetic context. Unfortunately IR is rarely used to identify this precise free ligand5. Low Frequencies remain at acceptable levels in both calculations.
Supplementary Information
W conformation
Item Value Threshold Converged? Maximum Force 0.000017 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.001192 0.001800 YES RMS Displacement 0.000399 0.001200 YES Predicted change in Energy=-8.980063D-09 Optimization completed.
Low frequencies --- -5.8072 -0.0002 0.0005 0.0005 3.5184 5.2157 Low frequencies --- 19.6136 22.6018 23.8401
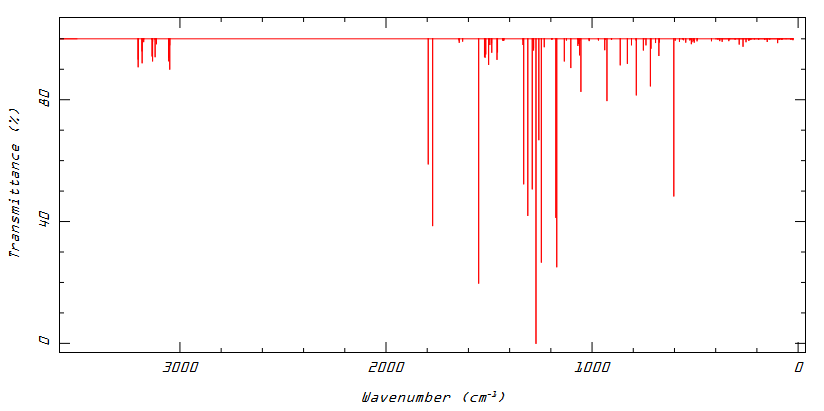
U conformation
Item Value Threshold Converged? Maximum Force 0.000047 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.001233 0.001800 YES RMS Displacement 0.000307 0.001200 YES Predicted change in Energy=-2.177520D-08 Optimization completed.
Low frequencies --- -8.2307 -7.5474 -5.1189 -0.0005 0.0004 0.0007 Low frequencies --- 25.2360 25.3478 33.6010
Fluorination Effects
The input coordinates of 1a were taken from the recorded crystal structure in reference 1, found using the Cambridge Crystal Structure Database, and alkyl/perfluoro chains removed/replaced accordingly. Initial optimisations entirely to the 6-31G(d,p) level (with LanL2DZ pp for Thallium) took prohibitively long to converge (10h38min on the cluster) and so a slightly less intensive basis set selection was specified, as shown in fig. 8. While nosymm was specified as a keyword (which relates to electronic symmetry), no nuclear symmetry was imposed on the complexes either, in part to allow for a broad range of Tl-arene interactions to be accessible by the optimisation algorithms. To ensure the convergence a frequency calculation was done[6]. Given the success of this job all subsequent calculations on 1a-d were done with this combination of basis sets.
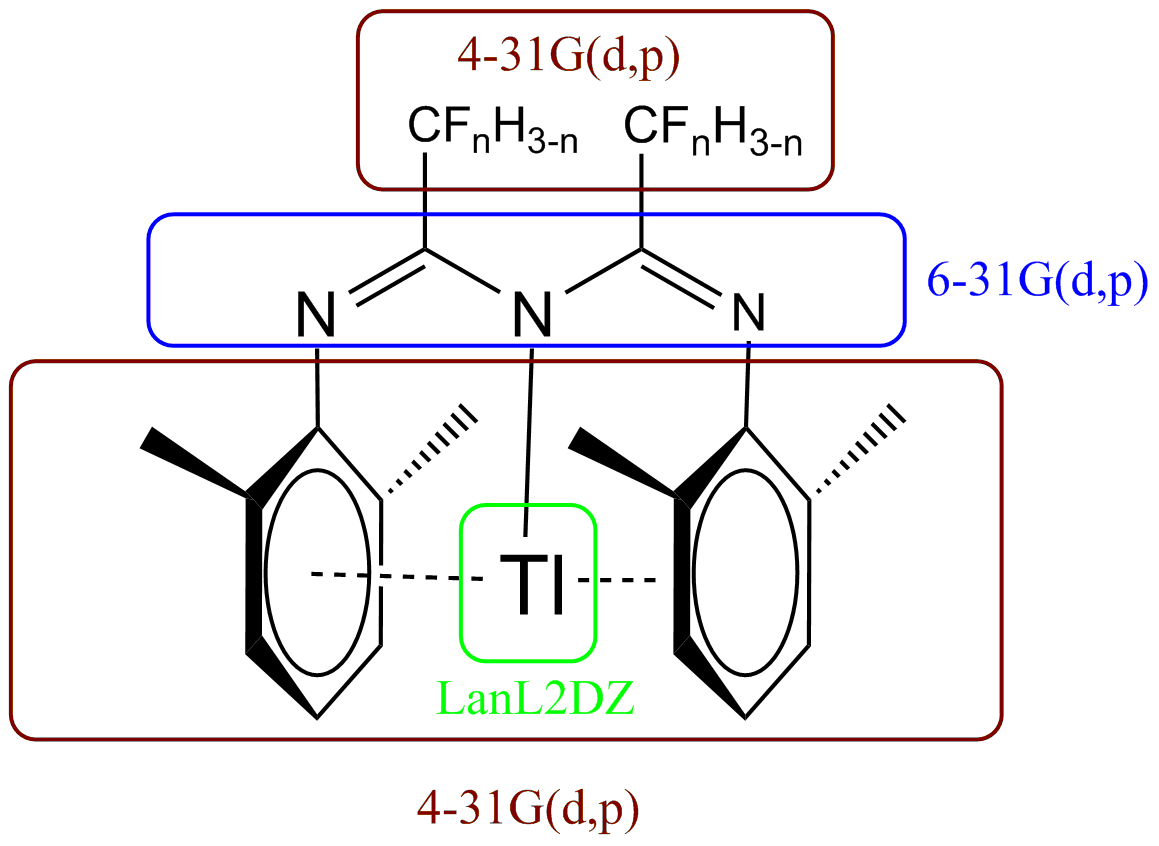
The higher basis was specified for the 'backbone' fragment to ensure an accurate W motif and to allow a better appraisal of the nature of the N→Tl bond in later analysis. (d,p) polarisation was still deemed necessary in the chain groups due to:
- The frequent invocation of polarisation caused by F in discussions of fluorinated ligands
- The still dubious nature of the Tl-arene contacts requiring still reasonably high level simulation
Input parameters for 1b-d were conducted by replacement of F by H in the input file for the successful 1a in Gaussview, with no further mechanical optimisation prior to initiating the job.
|
|
|
|
|
|
|
|
The immediate feature of note about this data is the extremely consistent energetic difference between the levels as n is varied by one. It should not merely be concluded, however, that this is prescribed by the nearly identical input parameters: the methyl rotations are accessible by the computation and so the lowest energy conformers of 1b and 1c are unlikely to be the same. Also the relative increase in 'fluorination level' is not the same each time ie. it is doubling between b and c, yet only increasing by 50% between c and d, yet the energy difference is identical. This latter point is in fact the most interesting outcome of the treatment: The energetic benefit of fluorination does not decrease as the level of fluorination itself increases (intuitively one may assume that it should diminish slowly), nor is it in any way dependent on the conformation.
Even given that SCF is employed here, the differing atomic orbitals employed on F by the theory were thought to be unlikely to affect the optimisation in the same way each time. It may, however, be a symptom of the low basis set used on those atoms.
The effect of dipoles on solubility/reactivity is coupled highly to the size and shape of a molecule and should not trivially be used to predict such concepts as reactivity, but in this case, with 1a-d essentially conformationally locked and containing the same number of atoms, their comparisons are justified. Unfortunately the identity of the dipole moments does not seem to correlate across the entire series 1a-d with fluorination level, deviating drastically in both magnitude and direction in a (see table in next section). This may be because of the effective cancelling of the polarity of all C-F moieties in this case (within the methyl, the group itself will still be highly electron withdrawing). It is speculated that due to this the majority of the dipole will be caused by C=N fragments. There is also likely a large difference in charge between Tl and N, aligning the dipoles directly down in most cases.
The kinetic and steric stability of 1 will of course also be affected between a and d but in the absence of molecular dynamics this is not currently quantifiable.
MO Analysis/The Tl-Ar bond
Further to the discussion of the concept of a bond given earlier, an attempt will be made to compare the extent of 'thallium arene complex' behavior in the varyingly fluorinated molecules 1a-d. Unfortunately, N-Tl distances (the author would hesitate to call them bond lengths as they are drastically in excess of the sum of covalent radii) have not been found to offer much useful information; in truth, there is no relationship to the fluorination level of the ligands (although the 1a distance correlates nicely with that found in the crystal structure of the compound upon which it was based1, with 0.5% relative error). Hence we must explore the frontier orbitals of the systems.
None of the HOMOs present in a-d have considerable electron density on thallium and so the HOMO-1 will be used for clarity.
| 1a | 1b | 1c | 1d | |
| Second from Highest Occupied MO for 1a-d | 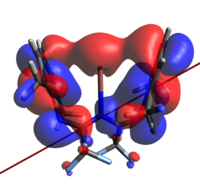
|
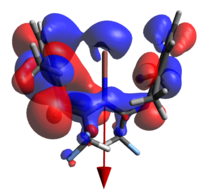
|
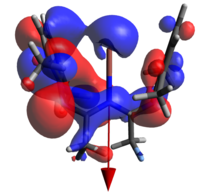
|
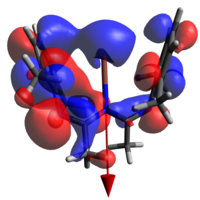
|
|---|---|---|---|---|
| N→Tl Bond Length | 2.683Å | 2.659Å | 2.725Å | 2.680Å |
The geometry of the two rings about the metal (ie dihedrally slipping) is to an extent enforced by the fluoromethyl repulsions, but affords orbital overlaps that are not consistent with the established metal-arene complex MOs. Indeed, even had the geometry been much less distorted, this would still not have been the case as d orbitals on Tl are treated as corelike by this basis set, so are unlikely to adequately interact. The identity of the atomic orbital originating from the Tl center which is interacting was the subject of some deliberation before it was concluded to be an extremely polarised 6s function, to the extent that the majority of the electron density is on the other side of the Tl from the N. All four orbitals are also all ostensibly not symmetric, with one of the rings interacting much more strongly than the other.
It was thought that the larger overlap about the metal in a and d relative to the middlingly fluorinated variants is a result of the polarisation of the R groups (that is to say, the methyl groups not present on the ring). Unfortunately the dipole moments presented by these calculations are not inherently helpful, as they do not allow us to justify how;
- The HOMO of d almost appears to be more similar to that of b than a (notice the right hand ring fragments)
- The extent that the electron density penetrates the Tl nucleus is largest in the extremes; one would expect it to decrease with increasing polarity.
Finally, we may say that the lack of a large number of energetically relevant orbitals containing significant Tl-C π character is consistent with bonding of this nature being only a small participant in the overall stability of the complex; a conclusion arrived at in both this work and the initial reference. As we will see in the next section, the ionic nature of the coordination/organometallic aspects of this compound can, in part, explain this.
Supplementary information
1a opt
Item Value Threshold Converged? Maximum Force 0.000070 0.000450 YES RMS Force 0.000010 0.000300 YES Maximum Displacement 0.001399 0.001800 YES RMS Displacement 0.000296 0.001200 YES Predicted change in Energy=-2.329841D-08 Optimization completed.
1b opt
Item Value Threshold Converged? Maximum Force 0.000018 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.001214 0.001800 YES RMS Displacement 0.000206 0.001200 YES Predicted change in Energy=-4.401129D-09 Optimization completed.
1c opt
Item Value Threshold Converged? Maximum Force 0.000015 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.000728 0.001800 YES RMS Displacement 0.000181 0.001200 YES Predicted change in Energy=-4.393900D-09 Optimization completed.
1d opt
Item Value Threshold Converged? Maximum Force 0.000017 0.000450 YES RMS Force 0.000003 0.000300 YES Maximum Displacement 0.001375 0.001800 YES RMS Displacement 0.000262 0.001200 YES Predicted change in Energy=-9.889967D-09 Optimization completed.
The U complex
An opt/NBO calculation[7] of the dicoordinate n=3 U conformation using precisely the same basis sets as the previous fluorination investigations was not able to converge in a reasonable time (calculation took 7hr 56min); inspection of the optimisation energies showed this was due to an oscillation about a minimum geometry occurring; a second opt was done using the coordinates of the penultimate structure before this oscillation as input.
Once this had converged[8] this the energetic difference between the output structures of 1a U and W was found to be 7.1*10-4Hartree; 0.45kcalmol-1. This is an extremely small difference (especially in comparison to that of the free ligand) and it can only be speculated that the barrier to interconversion must be very large; intuitively this is not an unreasonable assumption since it would likely involve a Tl atom not coordinated to any part of the triazapentadienyl fragment. Returning to the output energy, quantitatively it would suggests an extremely weak contribution from the metal arene interactions to the stability, although as can be seen in fig. Y these interactions are not significantly reduced in the U complex (at least around the HOMO-LUMO level). While the overall energetic outcome of the two conformations is consistent with what is stated in ref. 1, the source of the stability is in direct contradiction; That is to say, the SCF energy does not differ considerably between the two conformations and the electronic benefits are either negligible or negligibly different.
|
|
Dias et. al.'s principal explanation for the stability of bonding to the central nitrogen was 'charge considerations, the chelate effect, and/or steric effects'.1 If one may take charge to mean polarity then this is somewhat correct; NBO analysis of the U complex returns no Tl-N bonds, or bonds to Tl of any kind, and hence we may conclude that the bonding here is predominantly ionic. In comparison to some of the MOs of the W complex shown earlier this is indeed a large discrepancy; especially considering the relative increase in electron density found on the terminal nitrogens to begin with, implying orbital overlap is not inherently useful in this case. Steric effects may play a part, but would actually favour the U as it contains less crowding/congestion around the Tl, and molecular mechanics optimisations have been found to favour the U type coordination for this reason.
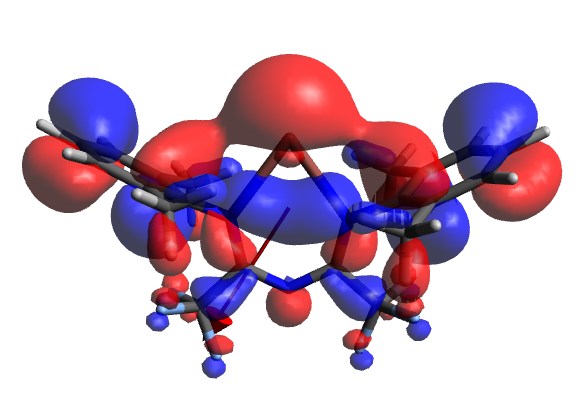
The MOs of the U complex (one of which is shown above) are non-trivial in nature and involve considerably more 'ligand' character, most notably the LUMO contains ostensible C-F σ* overlaps, and the HOMO appears to show a dxz orbital on Tl. As mentioned in a previous section, the Tl-Ar overlap is not sufficiently less than that in the W structure, and indeed appears to arise from similar fragment FOs. The significant diagonal directionality of the dipole remains unexplained, in light of the highly symmetric nature of the molecule.
Supplementary information - 1a U conformation opt/NBO
Item Value Threshold Converged? Maximum Force 0.000009 0.000450 YES RMS Force 0.000002 0.000300 YES Maximum Displacement 0.001267 0.001800 YES RMS Displacement 0.000247 0.001200 YES Predicted change in Energy=-8.692966D-09 Optimization completed.
Conclusions/Outlook
Data has been collected regarding 1a-d at theory levels previously unattained. A large volume of the interpretation of this affords conclusions which are significantly in conflict with those found in the literature, namely;
- The quantum mechincal free energy of the free ligand system favours the W conformation by a large margin (rather than the U slightly), offering a better explanation of the strict formation of the W complex in solution
- The highest occupied molecular orbital of the free ligand implies it is more electrophilic at the N atoms present at the edges (rather than evenly distributed among the three)
- However this cannot be used to deduce its coordination chemistry, as this has been shown to be mostly driven by ionic interactions with the metal
- The fluorination effect on stability of the complex is not dependent on the level of fluorination
- The most prevalent Tl-arene contacts in the W conformation likely arise from lone pairs and do not constitute a large benefit to the stability of the complex (at least over the U conformation).
Due to the short nature of this project, and the size of the molecule necessitating long computation times, several aspects of this metal/ligand system worthy of investigation had to be discarded. As such, should subsequent experiments be conducted, attention would be payed to:
- Using 19F NMR predictions to determine much more accurately the conformational identity of the ligand system synthesised (by comparison with literature)
- Determining the association energy of Thallium+ with [(2,6-Me)PhNC(CF3)]2N- to quantify better the stability of the U and W coordinated complexes
- Attempting to find the transition state/activation barrier for the interconversion of the two ligand coordination modes
- Looking into the effect of isotope labelling 203Tl on the calculated properties
- Producing a noncovalent interaction (NCI) surface for the perfluorinated system 1a, specifically with reference to the Tl-arene contacts
- Probing the second order effects of changing the chirality of the W conformation
References
- ↑ H.V.R.Dias, S. Singh, and T.R. Cundari, Angew. Chem. Int. Ed., 2005, 44, 4907
- ↑ M.F. Ernst, D.M. Roddick, Organometallcs, 1990, 9, 1586; M.F. Ernst, D.M. Roddick, Inorg. Chen., 1989, 28(9), 1624
- ↑ Trofimenko, S. Scorpionates: The Coordination Chemistry of Polypyrazolylborate Ligands Imperial College London, 1999
- ↑ O’Boyle et. al, J. Cheminformatics, 2011, 3, 33
- ↑ H.V.R. Dias, S. Singh, Inorg. Chem., 2004, 43, 5786; H.V.R. Dias, S. Singh, Inorg. Chem., 2004, 43, 7396
- ↑ S. Ingram, 2014 DOI:10042/27823
- ↑ S, Ingram, 2014DOI:10042/27842
- ↑ S, Ingram, 2014DOI:10042/27866
