Rep:Mod:Cah12

Transition States

A transition state is defined as the configuration where the potential energy is the highest; after this point the colliding molecules will always produce the products, assuming the reaction is irreversible .

Using Gaussian software the transition state of several reactions are established. The first transition state investigated is the [3,3] Cope Rearrangement, this is done by examining the activation energy and lowest energy of Anti and Gauche conformations. Then, the transition states of two separate Diels-Alder reactions are studied. Their molecular orbital mixing diagrams enabled the allowed and forbidden transition state geometry to be determined. Finally Diels-Alder endothermic and exothermic product conformations are simulated specifically looking at the reaction between cyclohexa-1,3-diene and maleic anhydride.

The two main modelling methods used are the Hartree Fock (HF) and B3YLP, these compute, optimise and determine the relative vibrational energies of each transition state. The HF method gives an approximate solution to the Schrodinger equation by using spin-orbitals (one-electron wavefunctions) in an interative numerical procedure until there is no change in its numbers on further calculations . The B3YLP is a more advanced method then HF, utilising the HF method to determine approximations for the exchange–correlation energy functional in density functional theory (DFT) to create hybrid functionals . B3YLP is a more accurate method than HF because DFT uses a function of the electron density to appropriate the potential felt on each electron whereas HF simply uses a mean potential field for the electronic repulsion term.

Throughout the report HF and B3YLP are compared and all conformations optimised.

Nf710 (talk) 22:44, 2 December 2015 (UTC) Good understanding of the theory used here and well referenced. A good basic understanding. The numerical methods for HF involve working out slater determinants for each arrangement of electrons then solving each in the Hamiltonian matrix to get the eigenfunction of the energy.

The Cope Rearrangement

(Section very similar to Mod:sm17121 Tam10 (talk) 16:05, 30 November 2015 (UTC))

The mechanism of [3,3]-sigmatropic shifts have been under much debate with theories citing concerted, dissociative or stepwise pathways and were investigated in detail by Houk et al. DOI:10.1021/ja00101a078 . Currently, it is well documented that sigmatropic shifts proceed by a boat or chair transition state in a concerted fashion. Below is the structure and concerted rearrangement of 1,5-dienes commonly associated with the Cope Rearrangement.

The Cope Rearrangement

The aim is to locate the low-energy minima and transition structures of C₆H₁₀ so that the preferential concerted mechanism is confirmed. This is done by calculating the potential energy surface at maximum and minimum points of each conformer.

Optimising conformers of 1,5-hexadiene

There are twelve conformers of the 1,5-hexadiene molecule all with either gauche or anti-periplanar (anti-linkage) arrangements. These are optimised in GaussView using the Hartree Fock method and a 3-21G basis set. Below is the table of the results showing the structure, point group and energies of a representative sample for comparison.

Conformer	Structure	Point Group	Energy/Hartrees HF/3-21G	Relative Energy kcal/mol
Anti 1	Anti 1	C2	-231.69260230	0.04
Anti 2	Anti 2	Ci	-231.69253528	0.08
Anti 4	Anti 4	C1	-231.69097054	1.06
Gauche 1	Gauche 1	C2	-231.687716	3.01
Gauche 2	Gauche 2	C2	-231.69166700	0.62
Gauche 3	Gauche 3	C1	-231.69260231	0.00
Gauche 5	Gauche 5	C1	-231.68916020	1.91

As can be seen from the table above, Gauche 3 is the lowest relative energy conformation of 1,5-hexadiene. Therefore Gauche 3 is the conformation most likely to represent the transition structure in the Cope Rearrangment. Its stability can be explained by the favourable orbital overlap between the C=C π orbital and the vinyl proton . In addition, the distance between the two vinyl groups are significantly further apart in comparison to the other conformations, this reduces unfavourable repulsions and is consequently preferred due to reduced steric effects. The highest energy conformer is Gauche 1 with a relative energy of 3.10 Kcal/mol greater than the Gauche 3. This is due to the vinyl protons on the Gauche 1 conformer being closer in proximity and therefore will be more sterically hindered due to repulsions. A comparison between the orbital overlap of Gauche 1 and 3 can be seen geographically below, highlighting the vinyl repulsions in Gauche 1 and stabilising orbital overlap in Gauche 3.

Gauche 3	Gauche 1

Nf710 (talk) 11:32, 3 December 2015 (UTC)That isn't a gauche 3 conf. Its an anti conformer. if you look at the middle bond the R chains are 180 degrees apart. if you were to look at the proper the MO diagram you should see the vinyl groups being in close inphase proximity therefore giving favourable intactions. this is a more advanced study with graphical representation than your reference. The vinyl group are actually closer in the gauche 3, the twisting always them to in phase. Its a shame as your explanation was good with referencing.

Comparing HF/3-21G and B3LYP/6-31G*

Conformer Anti 2 is re-optimised using the B3LYP/6-31G* method. The bond lengths and dihedral angles for each method (HF and B3LYP) are compared. Angle 1 is represented by C1-C4-C6-C9 and angle 2 C4-C6-C9-C11.

Numbered optimised anti 2 B3LYP/6-31G* calculated molecule

Optimisation	Length C1-C4 (Å)	Length C4-C6 (Å)	Length C6-C9 (Å)	Dihedral Angle 1 (°)	Dihedral Angle 2 (°)
HF/3-21G	1.355	1.540	1.540	114.60	180.00
B3LYP/6-31G*	1.338	1.507	1.555	118.78	180.00

B3LYP/6-31G* produces a shorter bond length for the C=C bond (C1-C4) compared to the HF/3-21G calculation, the former method has optimised the molecule to a bond length consistent with literature (1.33 Å ).

The difference between the C4-C6 and C6-C9 is varied and therefore little conclusion can be drawn from this comparison.

Comparing the dihedral angles shows that for angle 1, B3LYP/6-31G* produces a larger value and for angle 2 they are identical. This indicates that for the dihedral angle optimisation HF is sufficient to produce an estimate close to the real angle.

Therefore, HF/3-21G can be used to find a simple approximation of the minimum geometries with a relatively low computational cost, and then this estimate can be refined through a small number of steps at a higher level of theory using B3LYP/6-31G*.

Nf710 (talk) 11:46, 3 December 2015 (UTC) Very nice comparison with literature, and good comparison of geoms. However your bond lengths for the B3LYP are slightly out. I am concerned you have used the wrong basis set. will have to check you energy. if you has uploaded the log files then i would have been to check.

Frequency Analysis

The frequency of the optimised Anti 2 structure is calculated using the B3LYP/6-31G* method. This shows that all the vibrational frequencies are real and positive and that this is indeed the minimum conformer for 1,5-hexadiene.

IR Spectrum of optimised Anti 2

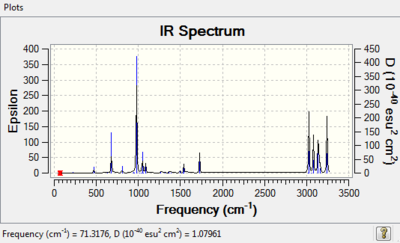
The vibrational frequencies are related to the second derivative of the reaction rate and allows determination of the structure at a specific point on the potential energy surface depending on the nature of the stationary point. In this case it shows that it is a minimum and therefore either a reactant or product conformation. The force constant (K) used in the equation of a quantum harmonic oscillator is also related to the vibrational frequency; it is square rooted. Therefore a negative K value would indicate an imaginary frequency where the spring would be pulling away from its position and lead to a negative energy, hence why it is imaginary as energy is always positive. Therefore due to all vibrational frequencies positive, and hence K being positive, this indicates the Anti 2 conformer is a minimum on the potential energy surface and therefore an observable low energy conformer.

Energies/Enthalpies	Total Energy/Enthalpy
Electronic and Zero-point Energies	-234.416285
Electronic and Thermal Energies	-234.408964
Electronic and Thermal Enthalpies	-234.408020
Electronic and Thermal Free Energies	-234.447878

This method provides information on the energy modes at a particular temperature as well as information on dissociation reactions and the entropic contribution of a specific conformer.

Optimising the "Chair" and "Boat" Transition Structures

The Cope Rearrangement proceeds through either a chair or boat transition structure, with the boat lying higher in energy due to a more strained bonds. Both conformations are approximated and optimised for comparison.

Chair Optimisation: Hartree Fock

Two allyl fragments are drawn with C_2h symmetry 2.20 Å apart and their structures optimised using the HF method.

Optimised Chair TS

The composition was further optimised to a TS (Berny) and an expected imaginary frequency of -818 cm¹ was observed. This shows that the transition state occurred on the potential energy surface. As can be seen by the animation below, the mechanism by which the reaction proceeds is a concerted syn-cycloaddition at this imaginary frequency.

Transition State Vibration -818cm-1

The imaginary frequency represents a maximum point on a potential energy surface indicative of a transition state. It is the point at which the reaction can very quickly form the reactants or the products (moving either side of the potential energy surface) and therefore does not "vibrate" like the reactants and products. This results in a negative force constant which is termed imaginary due to the fact that in the harmonic oscillator it is square rooted, and the square root of a negative number produces an imaginary number.

Nf710 (talk) 11:58, 3 December 2015 (UTC) Good understanding of the optimisation methods, would have been nice ot have the equations in here.

Chair Optimisation: Frozen Co-ordinate

Optimisation of the approximated transition structure can also be carried out by freezing the co-ordinates of the two terminal atoms in their lowest energy conformation 2.20 Å apart under HF and 3-21G basis set.

Optimised Frozen Chair

In comparison, the frozen co-ordinate method results in an increase in bond length, decrease in terminal bond length (1.382 Å to 1.389 Å) and an increase in imaginary frequency (-817.87 cm^-1 to -817.93 cm^-1). Although the difference is marginal, it is significant and indicates that freezing the terminal atoms leads to the bond lengths being closer to those observed in literature and the transition state will more readily form the reactants or products (depending on which side of the maximum it shifts). Consequently freezing the atoms is a potentially more reliable way of producing the optimised transition structure.

Boat Optimisation: QST2 Method

The Anti 2 structure is optimised using QST2 with a HF/3-21G basis set. The reactant and product structures are numbered so that the atoms can be monitored.

Numbered Anti 2 reactant (left) product (right)

After the first QST2 optimisation, the resulting conformation was not the desired product. This was due to only the linear sections of the molecule being translated between the reactant and product for optimisation, leaving C4-C3 in the reactant and C1-C6 in the product unmoved. Using QST2 is therefore not the most effective form of optimisation because it does not consider central bond rotation. As can be seen by the structure below, only the allyl chains interacted forming criss-cross bonds to each fragment.

QST2 Boat Conformer (first attempt)

A further optimisation was carried out so that central bond rotation of the 1,5-hexadiene would be recognised in the optimisation. The structure of the reactant and product was altered so that the dihedral angles were set to 0 and 100 degrees.

Amended Boat Conformers - Reactants (left) products (right)

Boat Transition State

The second optimisation was successful. An imaginary frequency of -840.07 cm^-1 was obtained, confirming the presence of the boat transition structure. Comparison to the chair structure shows that the boat conformation has a higher imaginary frequency and therefore will want to get back to either the reactants or products faster for the boat structure compared to the chair structure. This would be consistent with the theory that the boat conformation is more strained and therefore will more readily shift towards a more stable structure.

Therefore, the QST2 optimisation only works if the structure of the reactants and products is close to that of the transition state.

Intrinsic Reaction Co-ordinate

A route was plotted along the intrinsic reaction co-ordinate for the chair conformation. A series of points are created by taking small geometry steps in the direction where the gradient or slope of the energy surface is the steepest. This determines the lowest energy conformer as it maps the route through the minimum energy path to the local minimum on the potential energy surface.

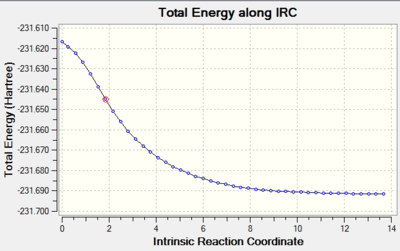
44 conformer geometries are obtained and the final product run again with a larger number of points until a minimum is reached.

Final structure along the intrinsic reaction co-ordinate

The slope of the graph shows the path taken by the transition structure as it moves from the point of high energy to the low energy well of the product. Due to the graph not showing a plateu at the lower energies, the lowest energy geometry was not found. A normal minimisation was carried out and the resultant structure seen was similar to that of the Gauche 2 conformer. Its structure is given below.

Optimized Minimum Energy Conformer

Nf710 (talk) 12:01, 3 December 2015 (UTC) well done for deducing the correct conf.

Activation Energies of the Transition Structures

Activation energies are compared to determine the lowest, and therefore preferred transition state; the chair or the boat. The chair and boat are re-optimised using HF/3-21G and B3YLP method for comparison.

Transition state and Method	Structure	C1-C2-C3 Angle (°)	C1-2 length (Å)	C1-6 length (Å)
Chair: Hartree Fock		120.53	1.389	2.021
Chair: B3YLP		120.173	1.406	1.986
Boat: Hartree Fock		121.688	1.382	2.140
Boat: B3YLP		122.270	1.393	2.207

A frequency optimisation confirms the presence of the transition state structure, observed by a single imaginary frequency. The results show that for the boat and chair transition structures, there is little difference between the method used as both produced similar results, suggesting that for optimised transition states whose structures have been correctly approximated, the HF/3-21G method is sufficient to produce a reliable result.

Summary of energies (in hartree)

	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619320	-231.466705	-231.461345	-234.585000	-234.414909	-234.408968
Boat TS	-231.602802	-231.450933	-231.445305	-234.556110	-234.402342	-234.396008
Reactant (anti2)	-231.692535	-231.539539	-231.532566	-234.559705	-234.468100	-234.461860

*1 hartree = 627.509 kcal/mol

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.70	44.69	33.34	33.19	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	41.26	41.32	44.7 ± 2.0

For the activation energies, B3LYP/6-31G* produced results which correlated with the experimental data showing that this method is more reliable. In comparison to the geometries which did not vary with basis set, the activation energy varied significantly with basis set. This shows that a smaller basis set, such as the B3LYP/6-31G*, is required because they do not change as much throughout the reaction compared to activation energies. The largest activation energy was seen at 0 K. This can be explained by the reduced thermal motion at low temperatures, so that more energy is required to get over the activation energy barrier. The smallest activation energy was seen for the chair and therefore this appears to be the prefered conformation.

Nf710 (talk) 12:16, 3 December 2015 (UTC) Your energies for all the confs here are wrong. therefore you activation energy is quite out. I think you must have used the wrong basis set. possible 631G**. however the report its self was very good an clearly set out, easy to read with good arguments and explanations. just a shame you got the energies wrong.

The Diels-Alder Cycloaddition

Ethylene and Cis-Butadiene

Pericyclic reactions involve a diene and dienophile which react in a concerted fashion to produce a new cyclic ring. The common reactions are cycloaddtions, singmatropic re-arrangments, and electrolytic reactions; below describes the cycloadditon between ethylene (dieneophile) and cis-Butadiene (diene) to form cyclohexane.

The geometry and energy of 1,3-Butadiene is optimised using the AM1 semi-empirical molecular orbital method, with a dihradral angle of 0° between the four carbons and an angle of 124.90° (C1, C2, C3 & C2, C3, C4) to produce the cis diene complex. Its optimised structures and molecular orbitals can be seen below where the optimised butadiene has a C_2v point group and therefore a plane of symmetry along its axis.

Optimized Butadiene structure

Optimized Ethylene structure

The molecular orbitals show the symmetry of the HOMO and LUMO. It is useful to observe these symmetries because it determines whether the cyclo-addition is allowed or forbidden.The HOMO for butadiene is anti-symmetric to the plane whilst its LUMO symmetric. For ethylene the HOMO is symmetric to the plane and the LUMO anti-symmetric. Therefore, due to the HOMO of the diene and LUMO of the dienophile being of the same symmetry, they will have good orbital overlap and the reaction is allowed.

Ethylene LUMO	Ethylene HOMO

Butadiene LUMO	Butadiene HOMO

The transition structure of the cyclo-addition between ethylene and cis-butadiene was first determined using the QST2 and the HF method. A distance of 2.0 Å was used between the terminal fragments of the butadiene and the ethylene.

Reactants and products of Diels-Alder	Transition state of Diels-Alder

(What you have for the reactants would be a problematic structure for Gaussian. It looks like an unstable structure, possibly an input structure. It looks like you've used it for the Jmol a few images down Tam10 (talk) 16:02, 30 November 2015 (UTC))

The transition state had an imaginary frequency of -818.46 cm^-1, therefore it can be assumed the transition state was obtained with the partial formation of the sigma bonds. It formed an envelope structure and its lowest frequency was 166.54 cm^-1 which shows that it is stable with respect to the normal mode.

Vibration of HF Diels-Alder TS

The transition structure is also examined using the QST2 and the AM1 semi-empirical method. This also produces an imaginary frequency at -956.61 cm^-1 confirming that the transition structure is formed.

Vibration of AM1 Diels-Alder TS

The vibrational animations above confirm that the cyclo-addition proceeds by a concerted syn-addition. Also, the HOMO of the AM1 transition state is shown below also confirming the mechanism of the reaction which shows that the HOMO-LUMO interactions will occur on the same face and simultaneously.

The HOMO of the transition state structure of the reaction of ethene with butadiene as calculated with AM1

(This is the wrong TS. You have the correct one earlier on (in the Jmols) Tam10 (talk) 16:02, 30 November 2015 (UTC))

Comparison of the two methods (HF and AM1) at forming the transition state shows that AM1 produces a higher imaginary frequency. A higher imaginary frequency means that the transition state will more readily form the reactants or products when you shift either side of the stationary point due to a steeper curve on the potential energy surface. Therefore the AM1 produces a transition state which is higher in energy and therefore a higher energy conformer. If this reaction was to run again, the activation energies should be calculated and a comparison made to determine which was the most effective method for cyclo-addition transition state simulations.

The bond lengths of the AM1 calculated transition state were examined below.

Carbon	Length (Å)
C1-2	1.38
C2-4	2.42
C4-5	2.12
C5-6	1.38
C2-3	1.39

(Which diagram are you referring to here? A length of 2.42A is unusual - seems like you've measured two carbons that weren't adjacent to each other Tam10 (talk) 16:02, 30 November 2015 (UTC))

The bond lengths for C-C single bonded sp² and sp³ hybridisation is recorded in literature as 1.47 Å and 1.54 Å respectively . Comparing this to the observed bond lengths in the transition state shows that for the bonds which are made and broken, these are less than normal C-C single bonds and therefore indicates delocalisation.

The Van Der Waals radius of the carbon reacting in the TS is 1.70 Å and the distance between the terminal fragments is 2.0 Å, showing that there is partial sigma bond formation. As can be seen by the vibrational frequency diagram above, the formation of the two bonds is synchronous which is consistent with the theory that Diels-Alder reactions proceed by a concerted cyclo-addition. This compares with the lowest positive frequency of 166.50 cm^-1 which indicates that the synchronous bond formation is the stable geometry at this normal mode.

(This value 2.0A seems to contradict your above table Tam10 (talk) 16:02, 30 November 2015 (UTC))

The MO formed in the transition state molecule is due to the overlap of the LUMO in ethylene and the HOMO in butadiene which mixes well due to their orbitals being similar in energy. This is because the HOMO of butadiene is higher in energy than the HOMO of ethylene, and its LUMO is much lower than that of ethylene, resulting in butadiene being more reactive towards nucleophiles. According to the Woodward Hoffman rules the cycloaddition is allowed due to a suprafacial reaction (the making and breaking of the bonds occur on the same face) and this can be seen by the MO's through its one conserved symmetry element. Consequently, it means that (4q+2)s + (4r)a must be odd.

Stereo-selective effects have not been fully investigated, the trans geometry may produce a different transition state and further simulations could be carried out to determine the stereo-selectivity of cyclo-additions.

Cyclohexa-1,3-diene and Maleic Anhydride

The concerted cyclo-addition of Cyclohexa-1,3-diene and Maleic Anhydride can proceed via an exo or endo transition state. In literature it is recorded that the endo is the favoured transition state it is the kinetic product due to its favourable HOMO-LUMO overlap as the C=O substituent is orientated towards the diene pi system. This produces a low energy transition structure. Investigation to confirm this is carried out using the AM1 semi-empirical molecular orbital method and QST2 optimisation.

Optimised diene structure

Optimised dienophile structure

Orbitals of cyclohexa-1,3-diene

LUMO	HOMO

Orbitals of maleic anhydride

LUMO	HOMO

The transition states were calculated using the optimised molecules and their formation was confirmed by a single negative vibrational frequency. For the exo product this was at -812.19 cm^-1 and had a low positive frequency at 60.83 cm^-1. Their HOMO and LUMO are plotted and energies compared along with their bond lengths.

Optimized TS of exo product

(Watch out - TS and product are two distinct things. You're talking about the TS here Tam10 (talk) 16:02, 30 November 2015 (UTC))

MO's for the exo product

LUMO	HOMO

For the endo product

Optimized TS of endo product

(This isn't the correct structure. Unfortunately I can't tell what happened as this is just the mol file and I can't converge on the same structure. You should have synchronous bond formation Tam10 (talk) 16:02, 30 November 2015 (UTC))

MO's for the endo product

LUMO	HOMO

The bond lengths of the endo and exo product are shown below with the molecule was labelled for clarity.

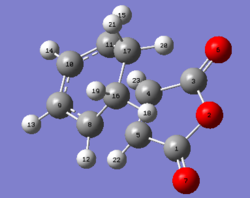
Bond	Endo Bond Length Å	Exo Bond Length Å
C10-11	1.396	1.341
C11-17	1.489	1.482
C17-16	1.522	1.519
C10-9	1.396	1.463
C4-5	1.410	1.349
C5-1	1.488	1.488
C8-5	2.170	2.328

The relative energies of the endo and exo product are 0.00 Kcal/mol and 0.67 Kcal/mol respectively, showing that the endo product in this case is more stable. However this result may vary depending on the experimental conditions and further calculations at varying temperatures could be performed. In addition, solvent effects were not taken into account and may also affect the results, therefore simulations run in varying solvent may be carried out for a more accurate comparison.

(0.67 Kcal/mol is roughly what you should be expecting, but it's unlikely that you should be getting it. Is there a calculation that I'm missing? Tam10 (talk) 16:02, 30 November 2015 (UTC))

The endo product had longer bond distances between the reacting carbons, where sigma bond formation occurs. This suggests that the endo form will be less strained as there is reduced sterics between the axial hydrogens on cyclohexa-1,3-diene and the bulky carbonyls on maleic anhydride. In addition, the secondary orbital overlap prefers the formation of the endo product and can be seen by the MO diagrams above; the HOMO of the endo product has a grater overlap between its orbitals, both between the reacting molecules and within the molecules themselves, increasing stabilisation.

(The conclusions here are a bit off due to having the wrong TS. Longer TS bonds does not suggest less strain. Often it is the other way around - a TS with longer bonds can suggest that it is being pushed apart by sterics, reducing orbital overlap and thus raising the energy. Again secondary orbital overlap is undeterminable due to the wrong structure. I can't see the MOs very clearly due to the angle you're using. You've demonstrated that you can use Jmol to show MOs - this would be an ideal situation to use it Tam10 (talk) 16:02, 30 November 2015 (UTC))

Conclusion

Comparison of B3LYP/6-31G* and HF/3-21G methods were made throughout. The Cope Re-arrangement showed that Gauche 3 had the lowest energy conformation due to secondary orbital overlap of the terminal alkyl fragments and that HF/3-21G was sufficient to produce the structure consistent with literature. The Anti 2 conformation shows that using the small step basis set B3LYP/6-31G* produced a more reliable geometry. In addition, optimisation of the boat and chair transition states confirmed the chair conformation as the lowest energy conformation. Overall it can be concluded that HF/3-21G can be used to find a simple approximation of the minimum geometries with a relatively low computational cost, and then this estimate can be refined through a small number of steps at a higher level of theory using B3LYP/6-31G*.

The stereochemistry of Diels-Alder reactions was examined by QS2T and AM1 empirical calculations. The endo product was formed preferentially through a concerted syn-cycloaddition under kinetic control which was explained by secondary orbital overlap in the transition state and confirmed by literature.

Not all effects in the Diels Alder reactions were not taken into account. The preference for endo product formation in the [4+2] cyclo-addition of cyclopentene to cyclopentadiene cannot be explained by secondary orbital overlap and therefore further investigation is required to explain this result. This also means that there will be more to the assumption above than simply calculating its lowest energy conformer and comparing its molecular orbitals.