Diels Alder reactions represent a very important category of organic reactions. Their reactivity has been studied thoroughly and the cycloaddition has been proven to proceed via a concerted bond formation.[1] Gaussian calculations have been used to illustrate and study this way of bond formation in Diels Alder reactions. In this experiment three such reactions have been studied, the relatively simple reaction between ethene and butadiene, the reaction between bezoquinone and cyclopentadiene, an important and widely used diene for Diels Alder. The last reaction studied was the reaction between o-xylylene and SO2. Here a variety of possible reactions with the mentioned substrates was explored and compared.
The way Diels Alder reactions were studied involves potential energy surfaces. Potential energy surfaces describe the energy as a function of distance between the atoms of the molecule. They can be used to improve the understanding of a reaction pathway. A maximum in a potential energy surface represents for example a transition state. For transition states one negative frequency can be found in a TS calculation. A transition state is an intrinsically short lived species and cannot be studied in detail in the lab for that reason. Therefore computational chemistry represents an important tool to improve the knowledge and understanding of transition states. A minimum represents a stable conformation of a molecule, meaning that the species can exist in that form. The lower the energy of a minimum the more stable the molecule. For example reactants and products both are found at a minimum of the potential energy surface. In Diels Alder reactions the products are generally more stable than the reactants and this is one driving force for the reaction. Both transition state and minimum have a gradient of 0 but the the second derivative, which represents the curvature of the surface is negative for the transition state and positive for the minimum. The software Gaussian was used to calculate energies for small parts of the potential energy surface. For this to be effective the reaction geometry of the studied reaction has to be well known. If it is not, it is easy to give the wrong input for the program and no useful result can be obtained.
Nf710 (talk) 14:17, 8 December 2016 (UTC) TS second derivative is negative in one dimension only, anymore and it is not a first order saddle point.
The Diels Alder reaction of butadiene with ethene
The concerted cycloaddition of ethene to butadiene is the simplest Diels Alder reaction possible. Nevertheless it is worth studying, in order to improve the understanding of this important class of organic reactions. Also even though it appears to be a simple reaction it still has interesting features.
MO diagram of the transition state
MO diagram
Figure 1: MO diagram
Figure 1: MO diagram of the transition state of the Diels Alder reaction between Butadiene and Ethene
Symmetry labels
For a reaction to proceed orbitals of the same symmetry have to be combined. Here the symmetry labels used are a for asymmetric and s for symmetric. The interactions of orbitals in bond forming reactions can be described using the LCAO model. When the two MOs which are combined are in phase, a constructive, boding interaction is observed. Out of phase interactions are described as destructive or antibonding. Both constructive and destructive interactions are non 0. As orbitals of different symmetries cannot be combined their interaction is equal to 0 and a reaction is forbidden if those orbitals are combined.
Upon consideration of the symmetries which describe the schematic representations of the molecular orbitals of the two reaction species discussed, it becomes clear that the two lowest energy orbitals which could combine (MO 2 and MO 5) have opposite symmetries. Hence the combinations observed are MO 2 and MO 6 which are both asymmetric orbitals and MO 3 and MO 5, both symmetric. This swap of symmetries, which ultimately represents a different energy spacing of diene- and dienophile-orbitals is characteristic for inverse electron demand Diels Alder reactions. So unlike the "classical" Diels Alder reaction, the reaction between ethene and butadiene has an inverse electron demand.
The energy profile of the reaction
Figure 1: MO diagram
Figure 2: IRC of Diels Alder reaction between Butadiene and Ethene
All Diels Alder reactions proceed via a high energy transition state. The height of the transition state represents the activation energy required. Normally this energy is provided in the form of heat in Diels Alder reactions. The products are lower in energy than the reactants. This is what drives the reaction. In figure 2 all these features are clearly visible.
Ethene
The ethene molecular orbitals reflect the orbitals used in the classical frontier molecular orbital theory. The HOMO corresponds to MO 5 in the MO diagram and to figure 3 in the table and is the totally symmetric orbital containing the 2 pi electrons. The LUMO (MO 6, figure 4) is the out of phase combination of the two p orbitals forming the pi system and has antibonding character with respect to the ethene molecule.
Ethene HOMO
Ethene LUMO
Figure 3: MO 5
Figure 4: MO 6
Butadiene
The HOMO (MO 2, figure 5) in the cis butadiene molecule is the combination of p orbitals with one node. It is bonding overall, however the node also adds some antibonding character to the MO. Two of the four pi electrons in butadiene are found in the HOMO. The LUMO (MO 3, figure 6) has two nodes, is unoccupied and antibonding overall due to the two nodes.
Butadiene HOMO
Butadiene LUMO
Figure 5: MO 2
Figure 6: MO 3
Combined orbitals of ethene and butadiene
TS MO 1: (figure 7) The molecular orbital TS MO 1 clearly corresponds to the combination of MO 2 and MO 5 of the two reactants. The bonding interaction is illustrated by the merging of fragment orbitals in the region of the in phase orbital overlap between the butadiene and ethene molecule. This interaction is clearly bonding. This MO is asymmetric.
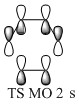
TS MO 2: (figure 8) The orbital TS MO 2 is another bonding interaction. It corresponds to the combination of MO 3 and MO 5 of the reactants. The orbital is slightly distorted as the ethene attracts all the electron density from the butadiene p orbitals on the outer carbon atoms. This orbital corresponds to the HOMO and is symmetric.
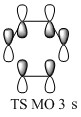
TS MO 3: (figure 9) This is clearly an antibonding orbital with its out of phase orbital interactions. It is out of phase combination of the same orbitals as in TS MO 2. This orbital is unoccupied and as it is lower in energy than the second antibonding orbital it is the LUMO. This is a symmetric MO.
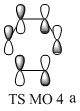
TS MO 4: (figure 10) This orbital corresponds to the out of phase combination of the orbitals combined in TS MO 1 (ie MO 2 and MO 5). Due to the basis set used in the calculation (PM6) the orbitals on the outer carbon atoms of the butadiene appear distorted. This is an asymmetric MO.
Figure 7: TS MO 1
Figure 8: TS MO 2 = HOMO
Figure 9: TS MO 3 = LUMO
Figure 10: TS MO 4
The change of the bond lengths over the course of the reaction
As illustrated by figure 11 and table 1 the bond lengths in reactants, transition state and product change during the reaction. The double bonds in the reactants are all 1.33 Å long, while the single bond in butadiene is 1.47 Å. The literature value for a C(sp2)=C(sp2) double bond is 1.32 Å, which corresponds well with the values generated by Gaussian. The corresponding single bond value for two sp2 hybridised carbons is 1.46 Å which also only differs slightly from the calculated value. Over the course of the reaction C1, C2, C3, and C6 change their sp2 hybridisation to a sp3 hybridisation and their bond lengths change accordingly. In the product the three bonds between C6-C3 are 1.54 Å long (lit. 1.53 Å). The bonds between one sp2 and one sp3 carbon (C3-C4 and C5-C6) are shorter at 1.50 Å (lit. 1.51 Å). The double bond between two sp2 hybridised carbons was 1.34 Å in the product (lit. as before 1.32 Å). It can be seen that all the values observed in the Gaussian calculation correspond well with the values mentioned in the literature. The transition state is an intermediate state between the reactants and products and the forming / breaking bonds are found to have intermediate values. As the transition state has no well defined hybridisations a comparison to literature values is not possible.[2] However, in the literature the value for the Van der Waals radius is reported as 1.72 - 1.80 Å for aromatic ring systems. This suggests that in the transition state there is already some bonding interaction between C1 and 6 and between C2 and 3 even though the bonds are not yet full single bonds. [3]
Figure 11: reaction scheme with labelled carbons
Bond lengths reactants in Å
Bond lengths transition state in Å
Bond lengths product in Å
C1-C2
1.33
1.38
1.54
C2-C3
no bond
2.11
1.54
C3-C4
1.33
1.38
1.50
C4-C5
1.47
1.41
1.34
C5-C6
1.33
1.38
1.50
C6-C1
no bond
2.11
1.54
Table 1
Bond formation in the reaction between ethene and butadiene
Figure 12: Illustration of the vibration leading to the bond forming reaction
Figure 13: Gif of the bonds forming
The vibration which corresponds to the reaction path is the imaginary, negative frequency at -526.70. It corresponds to a simultaneous out of plane stretch for both reactant molecules as shown in figure 12. The symmetry of the vibration confirms a simultaneous bond formation in this reaction, illustrated by figure 13. As the reactants are both symmetric molecules a concerted bond formation is expected. The lowest positive frequency at 136.16 corresponds to an in plane bend of the reactant molecules. The direction of the vibration shows that it does not have anything to do with the reaction between the two molecules discussed.
Nf710 (talk) 14:54, 8 December 2016 (UTC) Really well done section
The Diels Alder reaction between cyclopentadiene and bezoquinone
MOs of the reaction between cyclopentadiene and benzoquinone via the endo transition state
Filled bonding orbital
HOMO
LUMO
Unfilled antibonding orbital
Figure 14: scheme of TS MO2
Figure 16: scheme of TS MO1
Figure 18: scheme of TS MO4
Figure 20: scheme of TS MO3
Figure 15: symmetric MO 11
Figure 17: asymmetric MO 12 = HOMO
Figure 19: asymmetric MO 13 = LUMO
Figure 21: symmetric MO 18
The molecular orbitals in the endo transition state can be correlated with the molecular orbitals schematically presented in the MO diagram for the Diels Alder reaction between ethene and butadiene (the schemes shown before were used without alteration). In this correlation (figure 14 - 21) MO 11 would correspond to TS MO 2, MO 12 to TS MO 1, MO 13 to TS MO 4 and MO 14 to TS MO 3. The symmetries established for the MO diagram correlate with the symmetries exhibited by the MO of the transition state for the reaction between cyclopentadiene and benzoquinone. However the ordering is slightly different due to the different relative energies of the MOs in both reactions. This is due to the fact that the reaction between cyclopentadiene and benzoquinone is a normal electron demand Diels Alder reaction.
MOs of the reaction between cyclopentadiene and benzoquinone via the exo transition state
Filled bonding orbital
HOMO
LUMO
Unfilled antibonding orbital
Figure 22: scheme of TS MO2
Figure 24: scheme of TS MO1
Figure 26: scheme of TS MO4
Figure 28: scheme of TS MO3
Figure 23: symmetric MO 20
Figure 25: asymmetric MO 22 = HOMO
Figure 27: asymmetric MO 24 = LUMO
Figure 29: symmetric MO 26
The molecular orbitals in the exo transition state can be correlated with the molecular orbitals schematically presented in the MO diagram for the Diels Alder reaction between ethene and butadiene (figure 22 - 29). In this correlation MO 21 would correspond to TS MO 2, MO 22 to TS MO 1, MO 23 to TS MO 4 and MO 24 to TS MO 3. The symmetry correlation follows the same trend as before for the endo reaction.
Electron demand
This reaction is a normal electron demand Diels Alder reaction. This is due to the fact that the dienophile , with the two electron withdrawing carbonyl groups is electron poor and the diene is an electron rich species. In fact cyclopentadiene is a classic reagent for Diels Alter reactions and is known to yield good results with a variety of dienophiles.
Energy barriers
Nf710 (talk) 15:01, 8 December 2016 (UTC) You must state what level of theory you are doing it at.
Energy of reactants in kJ/mol
Energy of transition state in kJ/mol
Energy of products in kJ/mol
Endo-reaction
-1510617
-1510549
-1510665
Exo-reaction
-1510615
-1510542
-1510664
Table 2
Taking into account the energies tabulated in table 2 the activation energies for the exo and endo reaction can be determined (table 3). The endo activation energy is 67 kJ/mol while the activation energy for the exo reaction is 73 kJ/mol. This confirms that the endo reaction path is the preferred one, as less energy is required for it to proceed. Therefore the endo product is the kinetic product. The stabilization energy of the endo reaction is 49 kJ/mol, the stabilization energy of the exo product is 53 kJ/mol. This means that the exo product is the thermodynamic product.
Energy of activation in kJ/mol
Energy of stabilization in kJ/mol
Endo-reaction
67
49
Exo-reaction
73
53
Table 3
Nf710 (talk) 15:24, 8 December 2016 (UTC) I'm not sure what you have calculated the energies incorrectly. Possibly used the wrong basis set I am not sure.
Secondary orbital interaction
HOMO Endo transition state
HOMO Exo transition state
labelled carbons
Figure 30: asymmetric HOMO endo
Figure 31: asymmetric HOMO exo
Figure 32
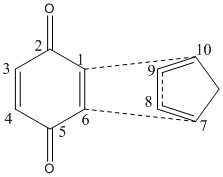Considering the molecular orbitals shown before it becomes clear why the reaction proceeds via the endo transition state. Secondary orbital interactions lower the transition state energy for the endo reaction. Considering figure 27 the orbitals on the carbons 8 and 9 on the cyclopentadiene can interact in phase with the orbitals between carbons 2 and 3 and and 4 and 5 on the benzoquionone. This in phase interaction lowers the energy of this comformation. In the exo reaction the orbitals on the diene are orientated away from the orbitals on the dienophile. A secondary orbital overlap is hence not possible and the reaction via an exo transition state less favorable.
Nf710 (talk) 15:28, 8 December 2016 (UTC) Despite unfortunatly calculating the energies incorrectly you have done everything else in this section well and shown the SSO extremely nicely.
Two possible reactions between o-xylylene and SO2
Reaction pathways
(These calculations should have been performed with just PM6 Tam10 (talk) 15:32, 22 November 2016 (UTC))
For the reaction between o-xylylene and SO2 three different reaction pathways are possible for the diene fragment outside of the six membered ring and connected by one side of the hexacycle. The most obvious reaction is the Diels Alder reaction using one S-O bond as the dienophile. As well known for Diels Alder reactions, this reaction can proceed via an exo or and endo arrangement of the reactants. The third possible reaction is a cheletropic rearrangement, meaning that only the S reacts in a cyclisation reaction with o-xylylene to form a five membered heterocycle.
Endo pathway
Exo pathway
Cheletropic rearrangement
Figure 33
Figure 34
Figure 35
(Here it looks like your exo TS is actually the endo TS. The S=O should be pointing away from the rest of the system Tam10 (talk) 15:32, 22 November 2016 (UTC))
Reaction energies
Energy of reactants in kJ/mol
Transition state energy in kJ/mol
Energy of product in kJ/mol
Endo path
-2252808
-2252802
-2252926
Exo path
-2252807
-2252802
-2252928
Cheletropic path
-2252807
-2252782
-2252917
Table 4
(It looks like you might be using "Sum of electronic and thermal Energies" instead of "Sum of electronic and thermal Free Energies". This excludes entropic contributions Tam10 (talk) 15:32, 22 November 2016 (UTC))
Using a B3LYP basis set, the energies of products, transition states and reactants have been calculated and compared. They are presented in table 4. The energies themselves do not hold much information therefore activation and stabilization energies were extracted from the data. When comparing the activation energies (ETS - Ereactants, as in table 5) it becomes clear that the exo reaction pathway is preferred, as it has the lowest activation energy with 5 kJ/mol. However the endo pathway is very close to this value wit 6 kJ/mol. The cheletropic rearrangement is disfavored with a 25 kJ/mol activation barrier. The energies of stabilization (Ereactants - Eproducts) are all in a similar range with 118, 121 and 110 kJ/mol for endo, exo and cheletropic pathway. This suggests that the exo reaction not only provides the most kinetically, but also the most thermodynamically favorable reaction pathway as it is also the most stabilized one.
(B3LYP is a DFT functional, not a basis set Tam10 (talk) 15:32, 22 November 2016 (UTC))
Energy of activation in kJ/mol
Energy of stabilisation in kJ/mol
Endo path
6
118
Exo path
5
121
Cheletropic path
25
110
Table 5
Graphical comparison of reaction pathway energies
Reaction energies in comparison
1200p/x
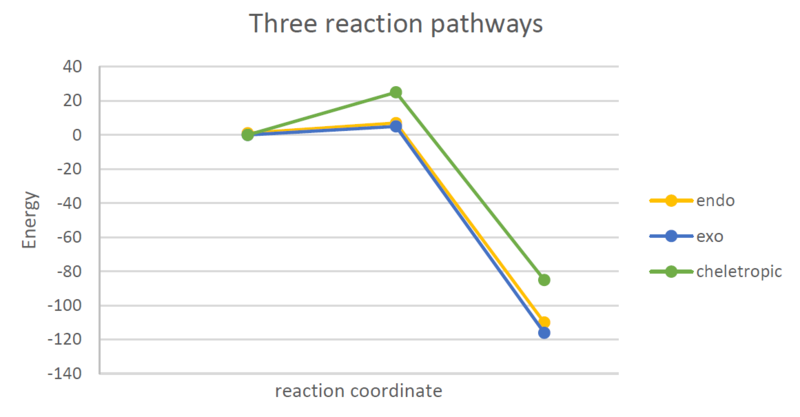Figure 36
In figure 36 shown above the three reaction pathways and their energies of products, TS and reactants are compared. Clearly the exo and endo pathway are very similar with the endo pathway slightly disfavoured. This suggests that the secondary orbital overlap which normally favors endo transition states does not come to play in this case. It is important to notice that SO2 is a small molecule and the orbitals localized on the oxygen are slightly mismatched to the carbon orbitals on the o-xylylene. Additionally the oxygen in the endo position is small with the orbitals in the wrong orientation for a good overlap, which could be the reason for the preference for the exo pathway.
Bond formation and aromaticity over the course of the reaction
Over the course of the reaction the S=O gets weakened to S-O as it takes part in the Diels Alder reaction. More importantly the six membered ring becomes an aromatic ring. The gain of aromaticity can be seen as one of the major driving forces in the reactions described above (consult figures 33 - 35 for a visualization of the reaction and bonding in the molecules). It is also one of the reasons for the small activation barrier seen in the Diels Alder reactions with o-xylyene and shows that o-xylylene is unstable and very reactive.
Reactions at the alternative diene of the o-xylylene
Figure 37ː Alternative diene
Upon investigation of the o-xylylene molecule it becomes clear that there is an alternative diene fragment of the molecule which could react as a Diels Alder diene. This is the diene which is part of the hexacycle as shown in figure 37. The reaction pathways (IRCs) have been calculated for an exo and an endo Diels Alder reaction at this part of the molecule with a PM6 basis set (Figure 38). The pathway resembles the pathways obtained for the other reactions with the products lower in energy than the reactants, however the activation energies appear higher and indicate that this reaction is less favored than the ones discussed before.
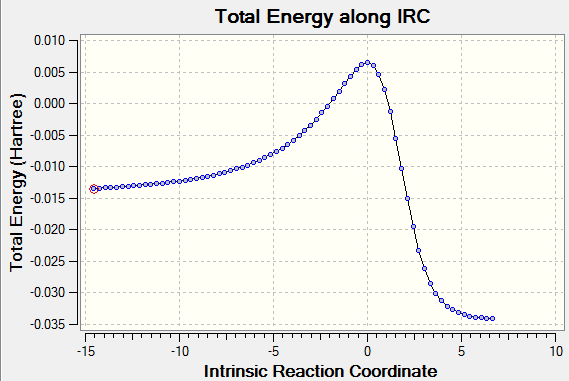
Figure 38ː IRC for endo product (generic for both reactions)
Reaction energies for alternative reaction pathways
The reactants, transition state and products have been optimized with a B3LYP basis set and a reverse in the relative energies of reactants and products was observed (table 6, products higher in energy than reactants). For this reason the energies of stabilization are negative in table 7. This unexpected change of trend could be attributed to the change of basis set. It also suggests that the reaction is unfavorable. Additionally the activation energies extracted from the B3LYP files are much higher than the ones observed in the reactions with the diene discussed initially. The reactions on this site are therefore not likely to occur. One of the reasons for this fact is that no aromoaticity is gained by the xylylene in this reaction and it hence becomes energetically less favorable. The activation energy for the endo pathway is however smaller and holds with the trend established earlier which states that generally endo pathways are favored over exo pathways.
Energy of reactants in kJ/mol
Transition state energy in kJ/mol
Energy of product in kJ/mol
Exo path
-2252800
-2252705
-2252736
Endo path
-2252800
-2252715
-2252744
Table 6
Energy of activation
Energy of stabilization
Exo path
95
-64
Endo path
85
-56
Table 7
Comparison of exo and endo HOMO
Upon investigation of the HOMOS of the two reaction transition states an explanation for the difference in activation energies can be found. In the endo HOMO the pi system on the reaction S and O atoms has a very effective overlap with the asymmetric orbital of the o-xylylene. The top phase of the second part of the diene MO overlaps simultaneously with the top phase of the same pi system, which makes the interaction more favorable. The HOMO of the exo transition state shows a good overlap between the pi system on SO2 and the asymmetric diene orbital. However another part of the diene MO overlaps with the antibonding orbital on the non reacting oxygen atom in SO2. The interaction is therefore less favorable and the exo transition state requires a higher activation energy than the endo transition state.
Conclusion
Three reactions have been studied computationally. The electron demand and the symmetry of the the molecular and fragment orbitals have been investigated for the reaction between ethene and butadiene. It has been found that the reaction has an inverse electron demand, which lies in contrast to "normal" Diels Alder reactions. Moreover the formation of the bonds and their lengths has been studied over the course of the reaction. The nature and bonding of the transition state could be better understood by this study. The second reaction was studied in regard to the molecular orbitals of the transition state. It could be confirmed that the reaction between butadiene and benzoquinone is a normal electron demand reaction. Moreover two possible reaction pathways were studied and the reasons for the preference of the endo route could be explained. The significance of secondary orbital overlap to activation energies was illustrated by MOs calculated by Gaussian. In the last computational experiment a more complex set of molecules was studied. O-Xylylene and SO2 can react in three different ways on the diene fragment which is outside of the hexacycle. All of those reaction pathways have been studied according to their energies on the potential energy surface and the most favorable reaction pathway was identified. Moreover the two possible Diels Alder reactions (exo and endo) on the second diene of o-xylylene, which is found within the hexacycle were studied. It could be explained why these reactions are less favorable than the ones described before and why their relative activation energies differ in comparison to each other. Overall the variety of Diels Alder reactions and the factors which influence their features were explored in this experiment.
