Rep:Mod:CWR3001
NH3 molecule
Information from the output
Calculation method: RB3LYP
Basis set: -56.55776873
RMS Gradient: 0.00000485 a.u.
Point group: C3V
Optimised bond distance: 1.01798 Angstrom
Optimised angle: 105.741 Degrees
Item table
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000070 0.001800 YES
RMS Displacement 0.000033 0.001200 YES
Predicted change in Energy=-5.785191D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Jmol Picture
test molecule |
Link: CAW116_NH3_OPTIMISATION.LOG
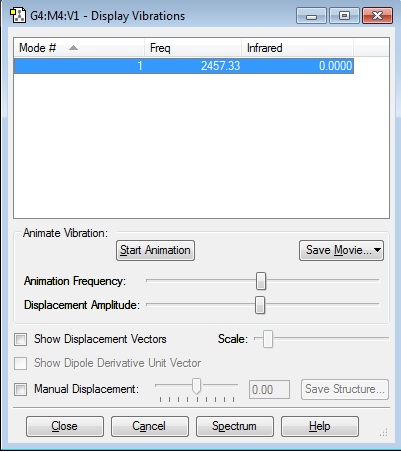
Vibration Calculations
Link: Caw116_nh3_optimisation_vibrations.jpg
Questions concerning the vibration calculations
Descriptions of the different vibration modes
| Vibration mode number | Description |
|---|---|
| 1 | Hydrogen 1,2 and 3 move towards each other (umbrella like) |
| 2 | Hydrogen 1 and 3 move towards each other, hydrogen 2 on top moves perpendicular to the H1 and H3 plane (from left to right), nitrogen moves towards and away from H1 and H3 |
| 3 | H2 and H3 move towards each other, H1 moves parallel to that bending plane |
| 4 | H1,H2,H3 move along the N-H bonds towards and away from the N |
| 5 | H3 and H2 move along the N-H bonds but asymmetrically, H1 stays still |
| 6 | H2 and H3 move along the N-H bonds symmetrically, H1 moves asymmetrically with respect to them |
1) How many modes do you expect from the 3N-6 rule?
- As ammonia consists of 4 atoms, one would expect 3*4-6 = 6 modes.
2) Which modes are degenerate?
- Modes 2&3 and 5&6 as they show the same frequency.
3) Which modes are "bending" vibrations and which are "bond stretch" vibrations?
- Bending: 1,2,3
- Stretching: 4,5,6
4) Which mode is highly symmetric?
- 4, as it does not change any symmetrical characteristics of the molecule.
5) One mode is known as the "umbrella" mode, which one is this?
- 1
6) How many bands would you expect to see in an experimental spectrum of gaseous ammonia?
- 4
Charge analysis
- Charge of N-atom = -1.125
- Charge of H-atoms = 0.375
The ratio of electronegativity is 0.7333, so the H's are expected to get 0.7333 of the total electron distribution in the molecule.
N2 molecule
Information from the output
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
RMS Gradient: 0.00000060 a.u.
Point group: D(infinity)H
Optimised bond distance: 1.10550 Angstrom
Optimised angle: 180 Degrees
Item table
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400983D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
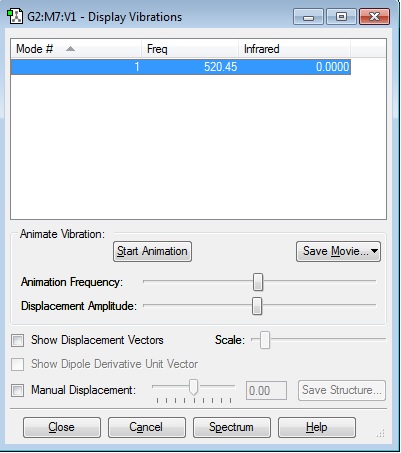
Vibrations
Link: caw116_n2_vibrations.jpg
Jmol Picture
test molecule |
Link: CAW116_N2_OPTIMISATION_3RD.LOG
H2 molecule
Information from the output
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
RMS Gradient: 0.00003809 a.u.
Point group: D(infinity)H
Optimised bond distance: 0.74289 Angstrom
Optimised angle: 180 Degrees
Item table
Item Value Threshold Converged?
Maximum Force 0.000066 0.000450 YES
RMS Force 0.000066 0.000300 YES
Maximum Displacement 0.000087 0.001800 YES
RMS Displacement 0.000123 0.001200 YES
Predicted change in Energy=-5.726834D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7429 -DE/DX = -0.0001 !
--------------------------------------------------------------------------------
Vibrations
Link: Caw116_h2_vibrations.jpg
Jmol Picture
test molecule |
Link: CAW116_H2_OPTIMISATION_4TH.LOG
Haber-Bosch process: N2 + 3H2 -> 2NH3
In the Haber-Bosch process ammonia is obtained from the elements nitrogen and hydrogen. As the entropy does not increase during the reaction, a very high pressure (200 bar) is needed. Moreover, as the process is exothermic, the reaction favours a low temperature (Le Chatelier). However, due to the very stable triple bond in nitrogen, a high activation energy is needed, which is given by a high temperature. Due to that contradiction, Fe3O4 as a catalyst is used to lower the activation energy without decreasing the yield too much.
Link: http://www.chemie.de/lexikon/Haber-Bosch-Verfahren.html
Energies
E(NH3)= -56.5578 a.u. = -148 492.50 kJ/mol 2*E(NH3)= -296 985 kJ/mol E(N2)= -109.524 a.u = -287 555.26 kJ/mol E(H2)= -1.17854 a.u. = -3094.26 kJ/mol 3*E(H2)= -9282.78 kJ/mol ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -146.96 kJ/mol
The reaction enthalpy is quite far from the literature value (for aqueous NH3: -80.8 kJ/mol; for gaseous NH3: -46,1 kJ/mol) ( http://www.chemie.de/lexikon/Enthalpie.html ). Thus, one can assume that something must have gone wrong during the calculations.
Both, the reactants as well as the product are very stable. However, the triple bond in nitrogen is very stable and needs a lot of energy to be broken, which makes the reactants more stable.
Cl2 molecule
Information from the output
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
RMS Gradient: 0.00000632 a.u.
Point group: D(infinity)H
Optimised bond distance: 2.04164 Angstrom
Optimised angle: 180 Degrees
Item table
Item Value Threshold Converged?
Maximum Force 0.000011 0.000450 YES
RMS Force 0.000011 0.000300 YES
Maximum Displacement 0.000031 0.001800 YES
RMS Displacement 0.000043 0.001200 YES
Predicted change in Energy=-3.347443D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.0416 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Vibrations
Link: caw116_cl2_vibrations.jpg
There is only one vibration along the bond possible, but as the atoms equal each other, there is not dipole. Therefore there is also no change in dipole moment during the vibration. That is why the molecule is IR-inactive.
Jmol Picture
test molecule |
Link: CAW116_CL2_OPTIMISATION_2ND.LOG
Charge distribution
+/- 0.000 at both Cl-atoms.
Five molecular orbitals of my choice
Orbital 1
Link: Caw116_cl2_3s_bonding.jpg
The picture shows the molecular bonding orbital of the two 3s orbitals of the individual Cl-atoms. The two spherical orbitals merge together to give one sphere, so that you cannot distinguish to which atom the electrons belong to.
Orbital 2
Link: Caw116_cl2_3s_antibonding.jpg
This picture shows the antibonding orbital corresponding to the bonding orbital of the 3s atomic orbitals. As the orbitals are opposite phase they point away from each other. In between the orbitals there is a plane with a zero probability of finding any electron. Therefore, it is antibonding. In the case of Cl2 it is also occupied, so it does not result in a bond.
Orbital 3
Link: Caw116_cl2_2pz_bonding.jpg
The picture shows the bonding molecular orbital of the individual 2pz orbitals of the Cl-atoms. They overlap along the bond and therefore result in a sigma-bond. However in this case, there will not be a bond as there are higher orbitals (3p's) occupied (which Gaussian was not able to show after several attempts), whose overlap results in bonding.
Orbital 4
Link: Caw116_cl2_2pz_antibonding.jpg
In this picture you can see the corresponding antibonding molecular orbital to the 2pz bonding molecular orbitals. Clearly, the atomic orbitals are opposite phase and therefore an overlap results in bond breaking. This orbital is not occupied and should therefore be the lowest unoccupied molecular orbital (LUMO).
Orbital 5
Link: Caw116_cl2_2px_antibonding.jpg
In this picture you can see the individual antibonding p(x or y)-orbitals, which lie perpendicular to the bond. An overlap would result in a pi or pi* orbital. In this case it is a pi* orbital, as the orbitals are opposite phase and thus antibonding. This orbital lies higher in energy than the sigma-orbital. However, as this orbital is occupied additionally to the corresponding bonding-orbital, it does not result in a pi-bond.